无节点的含Hilbert核的完全奇异积分方程

庄雯雯，姚艳玲(吉林师范大学数学学院，吉林四平136000)

无节点的含Hilbert核的完全奇异积分方程

庄雯雯，姚艳玲
(吉林师范大学数学学院，吉林四平136000)

文中使用完全奇异积分的组成形式来研究无节点的含Hilbert核的完全奇异积分方程，旨在将无节点的含Hilbert核的完全奇异积分方程放在一个由很多封闭曲线且光滑互不相交的情况下来进行研究，并通过Fredholm方程推导出无节点的含Hilbert核的完全奇异积分方程的解.

含Hilbert核的特征方程;周期R问题;Fredholm方程

1 问题提出

其中f，A，B已给在L上，φ为未知函数，设它们都属于H，在A2(t)+B2(t)≠0于L上来讨论.

2 给出已知量

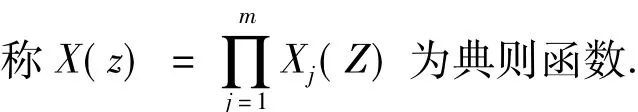
3 求解

由所研究的方程(1)可看出它是由含Hilbert核的特征方程和Fredholm方程构成的，可用算子形式写出(1)的形式为Kφ=K0φ+kφ，可将含Hilbert核的特征方程:

可求(3)的解也就是得出(1)的解.先求出(2)的解，将(2)式可化为周期R问题，在化成R问题时还需一个附加条件:Φ(+∞i)=－(－∞i)，所以，可将(2)式化成:

［1］路见可.解析函数的边值问题［M］.第二版.武汉:武汉大学出版社，2004.

［2］蔡海涛.平面弹性理论的周期接触问题［J］.应用数学学报，1979，2(2):181－195.

［3］杜金元.带Hilbert核的奇异积分方程的数值解法［J］.计算数学，1989(2):148－166.

(责任编辑:王宏志)

Abstract:This paper used the constitute form of fully singular integral to study no node containing Hilbert kernel completely singular integral equation，aimed at putting no node containing Hilbert kernel of completely singular integral equation inmany closed curve and smooth aswell asmutually disjoint situation is studied and through Fredholm equation deduced no node containing Hilbert kernel completely singular integral E-quation solution.

Key words:secular equation containing Hilbert kernel;the period R problem;Fredholm equation

No－node Com pletely Singular Integral Equation Containing Hilbert Kernel

ZHUANGWen－wen，YAO Yan－ling
(College of Mathematics，Jilin Normal University，Siping Jilin 136000，China)

O29

A

1008－7974(2011)04－0013－02

2010－12－28

庄雯雯(1986－)，女，吉林省安图县人，吉林师范大学数学学院在读研究生.