基于1范数的电阻层析成像图像重建算法

张玲玲 ，王化祥，范文茹

(1. 天津大学理学院，天津 300072；2. 天津大学电气与自动化工程学院，天津 300072)

电阻层析成像(electrical resistance tomography，ERT)可对封闭的管道或过程容器设备内部多相介质进行可视化测量，非常适用于以液相为连续相的多相流检测[1-3]．图像重建是ERT系统的关键问题之一．传统的图像重构方法，如共轭梯度法、Tikhonov正则化方法等均是基于2范数的优化方法．2范数处理适用于具有一定光滑性的信号重建，但不能有效地表征信号的稀疏性．ERT图像重建的信号通常具有很强的稀疏性，基于 2范数重建图像边界模糊，图像质量不高．为能更好地反映ERT重建信号的稀疏性，获得相对理想的重建效果，笔者采用基于 1范数的1l正则化最小二乘法(1l-regularized least-squares programs，LSPs)进行ERT图像重建，引入参数λ的自适应选择标准，将其与Tikhonov正则化方法进行比较，并通过仿真实验验证其有效性．

1 ERT图像重建

1.1 ERT系统工作模式

笔者的研究组开发的 ERT系统， 设计 16敏感电极阵列，采用相邻激励模式，如图 1所示．敏感阵列获取被测物场分布的投影信息，测量和数据收集所获得的物场信息将传给主控计算机，进行图像重建与显示，从而实现对被测物场的监测和控制[3-4]．

图1 ERT系统结构Fig.1 ERT system structure

1.2 ERT问题的数学模型

ERT技术是根据敏感场的电导率分布获得的物场媒质分布信息．在敏感长边界施加激励电流，当场内电导率分布变换时，导致场内电势分布变换，从而使场域边界上的测量电压发生变化．通过一定的图像重建算法可重建出场内的电导率分布．

根据似稳场理论的麦克斯韦方程，对于 ERT敏感场内任意一点满足[5]

式中：S为电流密度；σ为电导率；E为电场强度；φ为场内电势分布.由式(1)～式(3)，φ满足

ERT满足第2类边界条件，其形式可表示为

式中lI为电极l的注入电流．

1.3 ERT图像重建

ERT实现一般基于数值方法，分正问题和逆问题．正问题是已知敏感场内被测介质的电导率分布和敏感场的边界条件(外部激励电流)，求解电磁场的电势分布．通过有限元仿真软件(COMSOL)获得正问题的解．对正问题的求解可获取场内所有节点的电位信息，根据敏感电极边界的测量信息，求解敏感场内介质的电导率分布并重建出物场分布图像，即为ERT逆问题．逆问题由于测量数据少，存在严重的病态性，测量数据的微小扰动可导致解的剧烈变化甚至发散．因此，ERT问题的解决主要依赖于逆问题求解，即图像重建算法的计算精度和速度．

通常，电学系统方程进行线性化处理，ERT系统对应的方程为

式中：J是Jacobian矩阵；δU为随σ变化的边界电极间电压差：δσ为内部场域的电导率的变化值．为方便起见，式(7)转化为线性系统方程

由于矩阵 A 通常为大型稀疏的欠定矩阵，从而式(8)的解不存在或者不唯一．

2 算法分析

2.1 最小二乘法

求解病态方程组 =Ax y比较有效的算法是最小二乘法．对于 ERT系统来讲，灵敏度矩阵 A是欠定矩阵，方程组的解不存在或者不唯一，通过求最小范数最小二乘解作为其最优解，即

由于矩阵A不对称，求广义逆过程较复杂． 为简化求解，将欠定矩阵对应的线性方程组求解问题转化为对称矩阵对应的线性方程组求解，即将问题(9)转化为

求解的解析方法由下面的定理给出．

定理 1[6]对任意非零矩阵A ∈，方程组(10)解存在且 x = A+b为方程组的解．这里 A+是矩阵 A的广义逆．

问题转化成凸规划问题，通过相应的优化算法实现解此问题常用的算法有共轭梯度法和Landweber迭代法等[7-8]．

由于ERT系统的灵敏度矩阵A具有很强的稀疏性和病态性，对称矩阵TAA的谱趋近于零，导致问题的严重不适定性．为了克服病态性对问题求解精度的影响，一般采用 Tikhonov正则化方法[9]，其优化算法的形式为

式中λ为正则化参数．

式(12)的解析解表达式为

当λ是 ATA的正则点时，ATA−λI可逆．λ选择适当时，此方法可有效求解方程(9)的不适定性，但参数λ的选取需要凭经验选定．式(12)是用二次规划的优化算法得到式(13)的数值解，计算速度快，实时性强，对于ERT图像重建问题具有一定的效果．

以上算法是基于2l范数误差估计的计算方法，不可避免地会将原问题过度光滑，从而使不光滑的信息丢失，空间的分辨率不高．对于 ERT应用的大多数领域，被测区域的介质往往存在不连续性，灵敏度矩阵 A具有很强的稀疏性．基于 2范数的最小二乘法无法反映 ERT系统的稀疏性和不连续性，为了改善图像重建质量，借鉴Tikhonov正则化思想，改变误差估计方式，采用1l正则化的最小二乘法进行图像重建．

2.2 LSPs方法及其实现

对于方程(8)，当矩阵 A是稀疏的或其解具有可压缩性时，将方程(8)的求解转化[10]为

式(14)与式(12)不同之处在于罚函数用 1范数代替 2范数．LSPs方法是基于压缩传感理论发展起来的，特别针对大型稀疏线性方程组求解的新方法．既能克服问题的不适定性，同时能反映矩阵的稀疏性，避免2范数将问题过度平滑的缺点[11-12]．

内点法是目前求解 1范数优化问题最精确的算法，该方法由加州理工的压缩传感研究组提出[13]．整个过程是把 1 范数转化为不等式限制，再把不等式转化为门限函数进而去掉不等式．然后用迭代法进行求解．

为了去掉式(14)中的 1范数，引进新的变量iu，使其满足

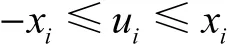
从而式(14)变换为

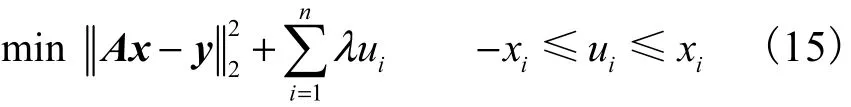
对式(15)中的限制条件 − xi≤ ui≤ xi定义对数门限函数(logarithmic barrier function)为

设置门限函数是模拟不等式的限制，从而有约束条件的二次规划问题式(15)变成无约束二次规划问题，即

参数t的变化范围为 0～∞．采用牛顿迭代法为基本原理，每次迭代令 t增大，增大的方式是按照序列，…, 其中μ＞1．

搜索方向可通过所表示的Newton系统的精确求解得到，即

式中：H为Hession矩阵；H = ∇2φt(x,u ) ∈Rn×2n；迭代的步长采用回追步长搜索方法．

该算法中，参数λ的选择是问题的关键，决定计算速度和成像质量．从前面分析可知，λ在之间变化，当0λ→时接近问题的解，当时， 0x→ ．如果选择过小，必然导致计算时间过长，实时性较差；如果λ选择过大，将会严重影响计算结果的准确度．事实上，λ取决于问题的稀疏程度．对于确定的方程(8)，的大小反映了问题的稀疏度，选择即可．不失一般性，令．如果矩阵的稀疏性较差，为得到更好的效果，令

3 仿真实验结果

采用有限元方法模拟不同流型分布验证本文提出的方法．ERT系统采用 16个电极，图像采用 812像素剖分．计算机配置为 Pentium(R)，2.93 GHz CPU、1G内存，以 MATLAB7.6为测试平台．分别用Landweber迭代算法、共轭梯度法、Tikhonov正则化方法和LSPs进行图像重建．表1是4种不同算法的重建效果，表2是4种算法的迭代次数与耗时．

由实验结果不难看出，Tikhonov正则化方法所获得的重建图像形状接近真实，但是边界模糊，且图像中存在干扰，需要进一步借助先验知识增强重构图像的鲁棒性．而LSPs算法中，可清楚分离不同物质，没有干扰信息，控制参数λ的选择具有自适应性．模型(1)、(2)，参数取值，模型(3)、(4)参数取值．LSPs算法迭代次数相对Tikhonov正则化方法迭代次数增多，实时性较差．有待进一步改进算法提高其实时性．

表1 图像重建算法的仿真实验结果Tab.1 Simulation experimental results of image reconstruction algorithm

表2 迭代次数与耗时Tab.2 Iterations and elapsed time

4 结 语

针对 ERT逆问题的严重不适定性和信号的稀疏性，采用基于1l正则化的最小二乘法，将罚函数项由传统的2范数改成1范数，改善了Tikhonov算法将问题过度平滑的缺点．采用该方法得到的重建图像，在不同介质分割的边缘处没有伪影，重建效果理想．

此外，基于1l正则化的最小二乘法中，参数λ的选择具有一定的自适应性，相对于较小即可．一般选择

［1］ York T. Status of electrical tomography in industrial applications[J]. Journal of Electronic Imaging，2001，10(3)：608-619.

［2］ Daily W，Ramirez A. Electrical resistance tomography[J]. Society of Exploration Geophysicists，2004，23(5)：438-442.

［3］ Dong Feng，Xu Yanbin. Application of electrical resistance tomography in two-phase flow measurement [J].Journal of Engineering Thermophysics，2006，27(5)：791-794.

［4］ 王化祥，汪 婧，胡 理，等. ERT／ECT双模态敏感阵列电极优化设计[J]. 天津大学学报，2008，41(8)：911-918.

Wang Huaxiang，Wang Jing，Hu Li，et al. Optimal design of ERT／ECT dual-modality sensing electrode array[J]. Journal of Tianjin University，2008，41(8)：911-918(in Chinese).

［5］ 毕德显. 电磁场理论[M]. 北京：电子工业出版社，1985.

Bi Dexian. Theory of Electromagnetics[M]. Beijing：Publishing House of Electronics Industry，1985(in Chinese).

［6］ 熊洪允. 应用数学基础[M]. 天津：天津大学出版社，2005.

Xiong Hongyun. Basis of Applied Mathematics[M].Tianjin：Tianjin University Press，2005(in Chinese).

［7］ 李 英，黄志光，冀海峰，等. 两相流参数测量 ERT图像重建算法的研究[J]. 浙江大学学报：工学版，2003，37(4)：382-385.

Li Ying，Huang Zhiguang，Ji Haifeng，et al. Study on image reconstruction algorithm of electrical resistant tomography for two-phase flow measurement[J]. Journal of Zhejiang University：Engineering Science，2003，37(4)：382-385(in Chinese).

［8］ 袁亚湘，孙文瑜. 最优化理论与方法[M]. 北京：科学出版社，2007.

Yuan Yaxiang，Sun Wenyu. Optimization Theory and Method[M]. Beijing：Science Press，2007(in Chinese).

［9］ 刘继军. 不适定问题的正则化方法及应用[M]. 北京：科学出版社，2005.

Liu Jijun. Regularization Methods and Application of Illposed Problems[M]. Beijing：Science Press，2005(in Chinese).

［10］ Kim S J，Koh K，Lustig M，et al. An interior-point method for large-scale 1-regularized least squares[J].IEEE Journal of Selected Topics in Signal Processing，2007，1(4)：606-617.

［11］ Candès E，Romberg J，Tao T. Stable signal recovery from incomplete and inaccurate information[J]. Communications on Pure Applied Mathematics，2005，59(8)：1207-1233.

［12］ Donoho D L. For most large underdetermined systems of linear equations，the minimal l1-norm solution is also the sparsest solution[J]. Comunications on Pure and Applied Mathematics，2006，59(6)：907-934.

［13］ Donoho D L. Compressed Sensing[J]. IEEE Transactions on Information Theory，2006，52(4)：1289-1306.