基于注入空间安全域的电网自愈决策

王 菲，余贻鑫

(天津大学智能电网教育部重点实验室，天津 300072）

近年来，世界上连锁大停电事故频繁发生[1-2]，社会经济损失巨大．促使人们展开了对电网自愈控制的研究，实现对预防、紧急和恢复控制的协调[3]．

紧急切负荷是防止连锁事故发生的重要控制方法[4]，是自愈控制研究的一个重要部分．文献[5-9]提出了基于灵敏度的最小切负荷计算，这类方法计算速度快、算法无收敛性问题，但其难以计及无功功率的影响计算精度不高；文献[10-12]利用最优潮流模型计算最小切负荷，可以较全面地计及各种约束条件、计算精度高，其不足之处在于优化算法自身的收敛性、鲁棒性问题，且计算时间较长．

在故障排除后，通过恢复性控制向被切除的负荷恢复供电则是自愈控制研究的另一个重要组成部分．负荷恢复的控制要求：一是快速、最大限度恢复停电负荷并且恢复操作的代价最小；二是在负荷恢复过程中必须满足安全稳定约束[13-14]，其重点是恢复过程中被切除负荷的恢复序列以及相应的发电调整，该负荷恢复序列与紧急控制的切负荷操作方案密切相关．文献[15]利用遗传算法求解负荷恢复方案，可以获得详细的恢复方案，但其未计及电压稳定约束，计算时间较长；文献[16]在负荷恢复模型中考虑暂态电压稳定约束，但该约束数学表达形式抽象、复杂，计算结果偏于保守．

对电网自愈控制的研究需解决2个难题：一是如何简洁直观地计及约束条件；二是如何建立并求解自愈控制模型．对于后者，由于紧急切负荷控制和负荷恢复控制既相互协调，又各具特点，因此在建模时既难于统一，又不能简单割裂．

笔者首先建立了综合考虑紧急切负荷控制以及负荷恢复控制的输电网自愈控制模型；同时，为提高求解效率，采用注入空间安全域[17]的方法给出了这些约束条件的线性化表达式．在文献[6]的基础上提出了求解自愈控制模型的扩展节点对集法，该方法在求解自愈控制方案的过程中考虑了紧急切负荷与负荷恢复之间的相互联系：在求解紧急切负荷后，可以获得负荷恢复控制中的负荷、发电节点操作序列，从而实现了对自愈控制模型的统一求解．最后，以新英格兰 39节点系统和河南电网为例，验证了本文中所建立的模型及算法的有效性．

1 电力系统的热稳定安全域

1.1 输电线路的有功电流

设网络由n +1个节点、nb条线路组成，其中节点0 为松弛节点．G : = {1，2，⋅⋅，ng}、L : = {ng+ 1，⋅⋅，n}分别表示发电机、负荷节点的集合；N = G∪L∪0表示全部节点的集合；用 B : = {1，2，⋅⋅，nb}表示全部线路集合；i、j分别为线路k的两端节点．

电力系统的静态安全约束包括节点电压幅值ℜU约束、线路电流约束ℜT和有功发电约束ℜGP，且有

式中：Ip∈Rnb为支路有功电流向量；P为节点有功功率注入向量；D为描述支路有功电流与节点有功功率注入之间映射关系的矩阵，D∈Rnb×n．

1.2 输电线路的无功电流

由电路理论可知：任一节点流入流出的无功功率代数和为零；任一基本回路的回路电压为零．

式中：B为基本回路矩阵； ub为支路电压向量，∈Rnb．结合式(3)及图论中关联矩阵的知识可得节点无功功率注入与线路首端无功潮流之间的数学关系

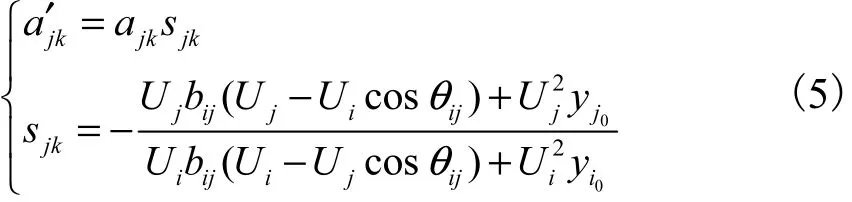
式中：ajk∈ A，A为降阶的节点支路关联矩阵；bij为线路 k电纳；θij为线路 k支路角；0iy和0jy 分别为线路i、j端的对地导纳．

1.3 电力系统的热稳定安全域

电力系统的热稳定安全域为满足潮流方程和线路电流约束的所有节点的复功率注入的集合，用ΩT表示，即

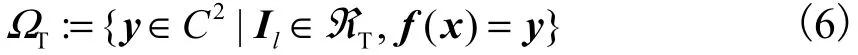
式中：f(x)= y为潮流方程；x为状态变量；y为节点的复功率注入向量．

在工程实际中，直接应用式(6)形式的热稳定安全域比较困难．若定义 Ikp、Ikq分别为线路 k的有功、无功电流，tan φk.＝Ikq/ Ikp，结合第 1.1 节、第 1.2 节可得有功、无功解耦的注入空间中的热稳定安全域，即

式中：S为描述线路首端无功电流与节点无功功率注入之间映射关系的矩阵，S＝H-1；m＝diag{cos ϕ1，，n＝diag{sin ϕ1，sin ϕ2， ⋅⋅ ，sinbnϕ}；IM为线路额定电流向量．为提高精度，式(7)中 D、S、m、n计算所需的变量均采用广域测量系统(wide area measurement system，WAMS)的实测数据．

2 基于热稳定安全域的自愈控制

2.1 排除线路过载的最小切负荷模型

自愈控制的第 1阶段为排除线路过载的最小切负荷模型，即

约束条件为

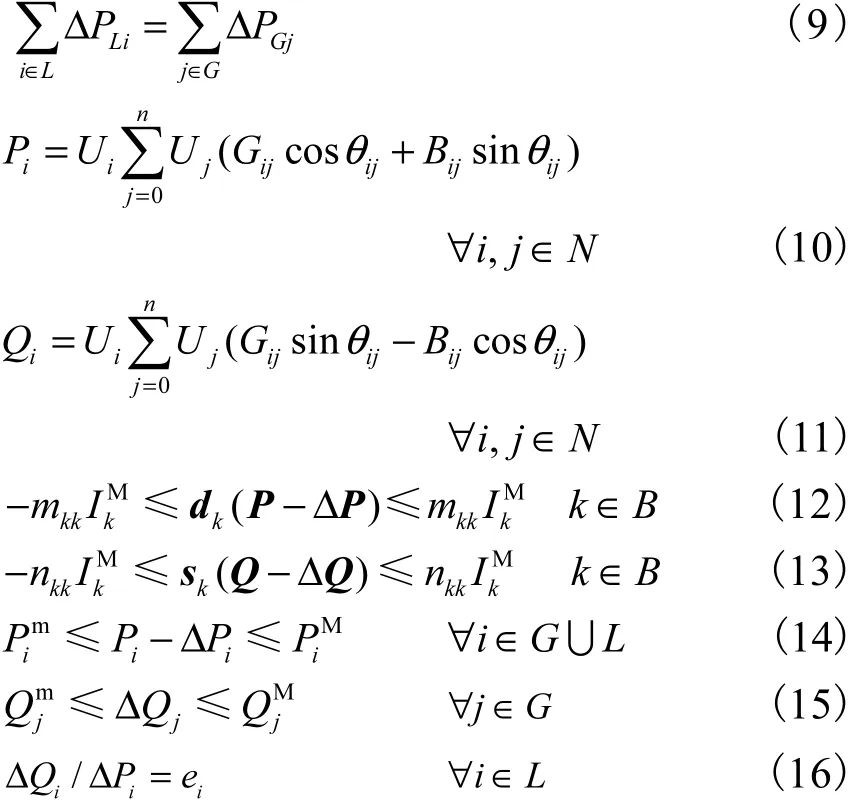
式(9)为系统的有功切负荷平衡约束；式(10)、式(11)为系统交流潮流方程约束；式(12)、式(13)分别为线路有功、无功电流约束；式(14)为节点有功注入的上下限约束；式(15)为发电机无功出力约束；式(16)为负荷节点功率因数约束．为节点权重系数向量；P、Q分别为节点初始有功、无功注入向量；ΔP、ΔQ 分别为节点的有功、无功切除向量；dk、sk分别为矩阵 D、S 的第 k 行向量；mkk∈ m；nkk∈ n；ei为负荷节点i的无功与有功注入的比值．

需要注意的是，当采用节点对集法求解上述模型时，ΔPGj(∀ j ∈ G)与ΔPL一样是唯一确定的．

2.2 恢复被甩负荷供电的最小发电调度模型

在故障排除后，自愈控制第 2阶段模型，即恢复被切除负荷供电的最小发电调度，其目标函数为

式中：|ΔPG|是由各台发电机出力绝对值组成的列向量；表示由各发电机权重所组成的行列向量．

由于恢复被切负荷的过程中，无论网络拓扑是否改变，发电的重新调度势必引起潮流分布的改变，有可能使个别输电线路重新过载，甚至使电网出现静态电压稳定问题．所以在考虑由式(10)～式(15)所给出的约束条件的同时，还必须计及静态电压稳定约束．由注入功率描述的临界割集静态电压稳定域边界的数学表达式[17]为

式中eu为电压稳定裕度．

在恢复向被切除负荷供电时所对应的系统发电调整ΔPG可划分为2部分，即ΔPG1和ΔPG2．其中切负荷阶段的发电机出力调整Δ PG1和已切除的等待恢复的负荷ΔPL是由第 2.1节所确定的．它们共同构成恢复被甩负荷供电的最小发电调度模型的输入量，而Δ PG2则为针对此输入量，对式(17)的目标函数进行求解所得的结果．

2.3 基于热稳定安全域的扩展节点对集法

文献[17]提出的节点对集法是以有功静态安全域作为基础，笔者对其进行了改进，使之能够求解第2.1节中建立的基于热稳定安全域的模型．

(1)将最有效操作节点对由(Lp，Gp)扩展为(Lp，Gp，Gq)．Lp、Gp、Gq分别为最有效负荷注入节点以及有功、无功发电注入节点．

(2)确定扩展节点对的切负荷量Δp，即

式中：dk,Lp、dk,Gp∈ D；sk,Lp、sk,Gp∈ S；Δp1、Δp2分别为由ΔIk有功、无功分量确定的切除量；ΔIk为线路 k的复电流越限量；eLp为Lp的无功、有功注入比值．

扩展节点对集法求解最小切负荷的步骤与节点对法相同，可参考文献[6]，此处不再赘述．

扩展节点集法所求得的最小切负荷方案ΔPL不仅给出了与任一切负荷操作相对应的切机操作，还给出了切负荷节点的操作序列．该操作序列根据线路过载量的降序确定(即切负荷量逐渐降低)，其与最大限度恢复负荷的要求一致，可以作为被甩负荷的恢复顺序．按该顺序恢复被甩负荷供电的最小发电调度模型的求解步骤如下．

步骤1 初始化计算变量：1GPΔ＝0，2GPΔ＝0．

步骤 2 恢复故障线路运行，并校验线路热稳定性．若有线路过载，则进行发电调整0GPΔ，并令2GPΔ=Δ PG0；否则继续步骤3．

步骤3 恢复ΔPL中位于节点对操作序列首位的被甩负荷及与其配对的发电节点的发电．恢复后，将该节点对从ΔPL中移除．

步骤 4 校验由式(10)～式(15)及式(18)构成的约束条件集．当存在违约时，通过求解式(17)所确定的发电调整Δ PG2来消除违约现象．

步骤5 修正最小发电调度计划．

步骤6 校验集合ΔPL中是否还有未被恢复的负荷节点：若仍有负荷未被恢复，则转步骤 2继续计算；否则，算法结束，最小发电调度方案由Δ PG1和ΔPG2共同构成．

对步骤2和步骤4中Δ pG1、Δ pG2均采用节点对集法求解．在求解过程中由约束条件k所求得的ΔpG为

式中：G1、G2分别为对约束条件 k最有效的增加、削减发电节点；ΔCk为约束条件k的违约量．

3 算 例

将以新英格兰39节点系统和我国河南电网为例来说明本文中方法的有效性．系统的最小静态电压稳定裕度eu＝ 0.15．

算例1 新英格兰39节点系统

图1为新英格兰39节点的系统拓扑及临界割集示意．系统静态电压稳定域的临界割集由线路L1-39、L3-4、L15-16组成．此时，若线路L15-16故障停运，出现线路过载．线路过载信息见表1．

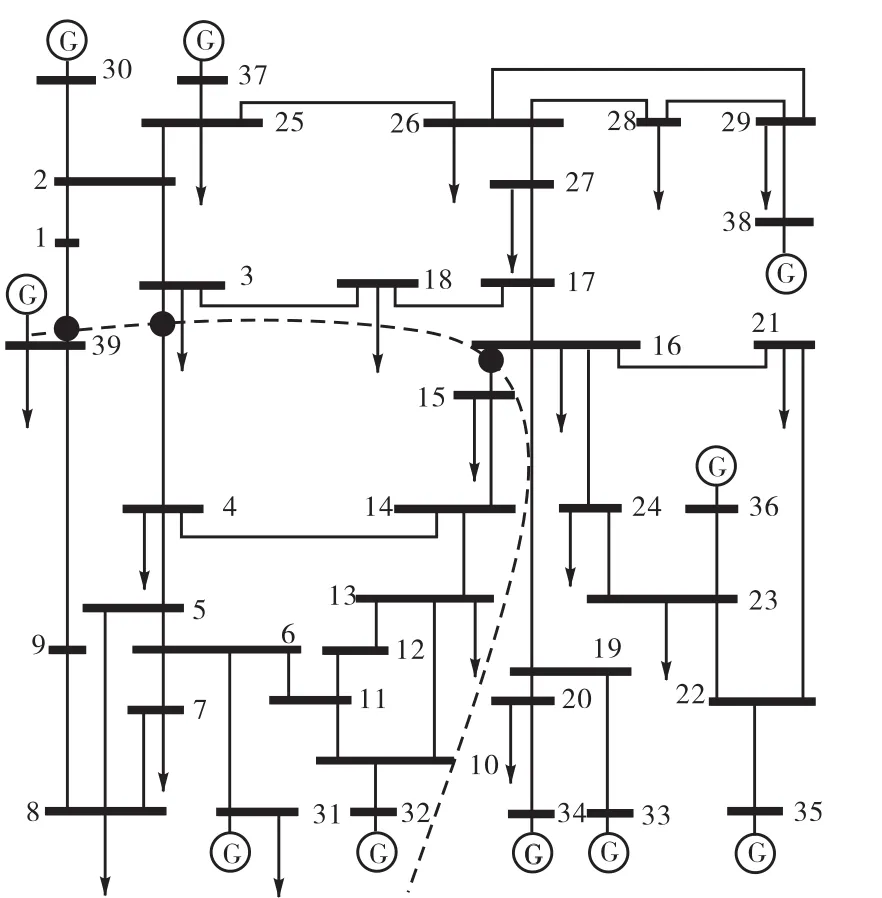
图1 新英格兰系统及临界割集Fig.1 New England system and its critical cut-set

表 2为采用扩展节点对集法求得的最小切负荷方案，其中切负荷为正，切发电为负．

表1 新英格兰系统线路过载信息Tab.1 Branch’s overload rates of New England system

表2 新英格兰系统最小切负荷方案Tab.2 Minimum load-shedding for New England system

图 2为在实施紧急切负荷控制前、后以及 L15-16故障排除恢复运行后系统中部分线路首端电流变化对比图．由图 2可见，恢复 L15-16运行后，线路L6-7的热稳定性降低，其首端电流值达到了 L6-7线路的电流限值．在进行负荷恢复之前应先进行一次发电调整，使线路 L6-7具有一定的热稳定裕度，如取为额定电流的 5%．表 3为恢复被切除负荷供电的操作方案，其中增加发电为正，切除发电为负．

图2 新英格兰系统紧急控制效果Fig.2 Effect of emergency control in New England system

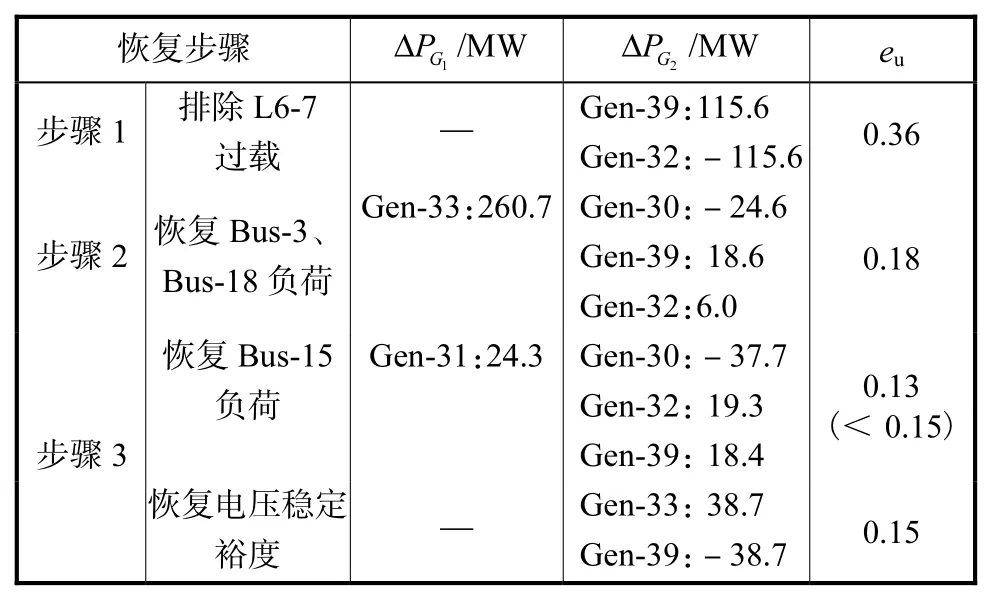
表3 新英格兰系统恢复负荷供电方案Tab.3 Restoration process of shed loads in New England system

图3为按表3的策略恢复负荷过程中，系统中接近热稳定临界状态的线路首端的电流变化．

图3 新英格兰39系统负荷恢复效果Fig.3 Effect of load restoration in New England 39 system

由图3可见，采用表3中的恢复方案，可以有效地避免恢复过程中再次出现线路过载问题；且系统的静态电压稳定裕度均不小于 0.15，因此该方案是有效的．

算例2 河南电网

河南电网包括973个节点、1 117条线路、145个负荷节点和86台发电机．当L335故障停运后，线路L17、L68、L143、L363出现过载．图 4为切负荷控制前、后，以及L335故障排除后的线路电流变化．由图4可知，恢复L335后，线路L91过载．

图 5为按照该策略恢复负荷过程中系统处于热稳定临界状态的线路首端电流变化．表 4为排除线路过载的最小切负荷方案．表 5为恢复被切除负荷供电的恢复策略．

图4 河南系统紧急控制效果Fig.4 Effect of emergency control in Henan system

图5 河南系统负荷恢复效果Fig.5 Effect of load restoration in Henan system

表4 河南系统最小切负荷方案Tab.4 Minimum load-shedding for Henan system

表5 河南系统节点系统恢复负荷供电方案Tab.5 Restoration Process of shed load in Henan system

4 结 语

本文中所建立的输电网的自愈控制模型综合考虑了线路复电流约束和控制过程中系统的静态电压稳定约束，并通过热稳定安全域和割集电压稳定域将约束条件表示为一组以节点注入功率为控制变量的线性化不等式，使得模型的数学描述十分简洁，从而提高了求解效率．

扩展节点对集法在求解自愈控制方案时，具有求解速度快，无收敛性问题的优点；同时，在求解过程中能够将紧急切负荷控制与负荷恢复控制紧密联系起来，由紧急切负荷模型所求得的最小切负荷方案以及负荷-发电节点对的操作序列即可作为求解负荷恢复模型中最小发电调度的输入量，从而实现对这2个子模型的统一求解．

［1］ U. S. -Canada Power System Outage Task Force. Final Report on the August 14，2003 Blackout in the United States and Canada：Causes and Recommendations[R].North American Electric Reliability Council，USA：Princeton，2004.

［2］ 李春艳，孙元章，陈向宜，等. 西欧“11. 4”大停电事故的初步分析及防止我国大面积停电事故的措施[J]. 电网技术，2006，30(24)：16-21.

Li Chunyan，Sun Yuanzhang，Chen Xiangyi，et al.Preliminary analysis of large scale blackout in western Europe power grid on November 4 and measures to prevent large scale blackout in China [J]. Power System Technology，2006，30(24)：16-21(in Chinese).

［3］ 万秋兰. 大电网实现自愈的理论研究方向[J]. 电力系统自动化，2009，33(17)：29-32.

Wan Qiulan. Theory study for self-healing of large power grid[J]. Automation of Electric Power Systems，2009，33(17)：29-32(in Chinese).

［4］ 袁季修. 电力系统安全稳定控制[M]. 北京：中国电力出版社，1996.

Yuan Jixiu. Power System Security and Stability Control[M]. Beijing：China Electric Power Press，1996(in Chinese).

［5］ 丁 明，李生虎，吴红斌，等. 基于充分性和安全性的电力系统运行状态分析和量化评价[J]. 中国电机工程学报，2004，24(4)：43-49.

Ding Ming，Li Shenghu，Wu Hongbin，et al. Analysis of power system operation state based on adequacy and security[J]. Proceedings of the CSEE，2004，24(4)：43-49(in Chinese).

［6］ 王 菲，余贻鑫，刘艳丽. 基于安全域的电网最小切负荷计算方法[J]. 中国电机工程学报，2010，30(13)：28-33.

Wang Fei，Yu Yixin，Liu Yanli. Minimum loadshedding calculation approach based on the security region in the power grid[J]. Proceedings of the CSEE，2010，30(13)：28-33(in Chinese).

［7］ 傅 旭，王锡凡. 静态安全分析中的联动切负荷算法[J]. 中国电机工程学报，2006，26(9)：82-86.

Fu Xu，Wang Xifan. New approach to load-shedding in static state security analysis of power systems[J]. Proceedings of the CSEE，2006，26(9)：82-86(in Chinese).

［8］ 苗峰显，白雪峰，郭志忠. 支路潮流越限控制的虚拟支路法[J]. 电力系统自动化，2009，33(14)：32-36.

Miao Fengxian，Bai Xuefeng，Guo Zhizhong. A virtual branch method for branch power flow off-limit analysis[J]. Automation of Electric Power Systems，2009，33(14)：32-36(in Chinese).

［9］ Roberto F，Antonio P，Enrico T. Load shedding：A new proposal[J]. IEEE Transactions on Power Systems，2007，22(4)：2086-2093.

［10］ Srivastava S C，Kurmar P. Optimal power dispatch in deregulated market considering congestion management[C]//Proceedings of the 2000 International Conference on Electric Utility Deregulation and Restructuring and Power Technologies. London，UK，2000：53-59.

［11］ Carolina M A，Luiz C P，Flavio G M，et al. MW and Mvar management on supply and demand side for meeting voltage stability margin criteria[J]. IEEE Transactions on Power Systems，2004，19(3)：1538-1545.

［12］ 王 刚，蔡兴国，马 平. 缺电损失最小化减负荷算法的研究[J]. 中国电机工程学报，2005，25(21)：45-50.

Wang Gang，Cai Xingguo，Ma Ping. Research of load shedding algorithm based on minimizing power outage cost[J]. Proceedings of the CSEE，2005，25(21)：45-50(in Chinese).

［13］ 蒋雷海，万芳茹，徐泰山. 电力系统故障恢复方法简述[J]. 电力自动化设备，2002，22(5)：70-73.

Jiang Leishai，Wan Fangru，Xu Taishan. Review on approaches of power system restoration[J]. Electric Power Automation Equipment，2002，22(5)：70-73(in Chinese).

［14］ 李文沅. 电力系统风险评估——模型、方法和应用[M]． 北京：科学出版社，2006.

Li Wenyuan. Risk Assessment of Power Systems—Models，Methods，and Applications[M]. Beijing：Science Press，2006(in Chinese).

［15］ 张志毅，陈允平，袁荣湘. 电力系统负荷恢复问题的混合遗传算法求解[J]. 电工技术学报，2007，22(2)：105-109.

Zhang Zhiyi，Chen Yunping，Yuan Rongxiang. Hybrid genetic algorithm for power system load restoration[J].Transactions of China Electrotechnical Society，2007，22(2)：105-109(in Chinese).

［16］ 瞿寒冰，刘玉田. 计及暂态电压约束的负荷恢复能力快速计算[J]. 电力系统自动化，2009，33(15)：8-12.

Qu Hanbing，Liu Yutian. Fast calculation of load restoration capability considering transient voltage constraint[J]. Automation of Electric Power Systems，2009，33(15)：8-12(in Chinese).

［17］ 余贻鑫. 电力系统安全域方法研究述评[J]. 天津大学学报，2008，41(6)：635-646.

Yu Yixin. Review of study on methodology of security regions of power system[J]. Journal of Tianjin University，2008，41(6)：635-646(in Chinese).

［18］ 余贻鑫，冯 飞. 电力系统有功静态安全域[J]. 中国科学：A辑，1990(6)：664-672.

Yu Yixin，Feng Fei. Active power steady-state security region of power system[J]. Science in China：Series A，1990(6)：664-672(in Chinese).