基于Matlab-simulink的航空重力仪陀螺稳定平台仿真*

王锦 柳林涛

(1)中国科学院测量与地球物理研究所动力大地测量学重点实验室，武汉430077) 2)中国科学院研究生院，北京100049

基于Matlab-simulink的航空重力仪陀螺稳定平台仿真*

王锦1，2)柳林涛1)

(
1)中国科学院测量与地球物理研究所动力大地测量学重点实验室，武汉430077) 2)中国科学院研究生院，北京100049

基于航空重力测量的独特优越性，研究了陀螺稳定平台在航空测量系统中的作用。运用Matlab simulink仿真模块建立单轴陀螺稳定平台稳定回路系统;建立修正回路数学模型，给定仿真条件下进行系统仿真并得出仿真结果;给出航空重力测量水平误差改正模型，并得出水平误差改正值。

航空重力测量系统;陀螺稳定平台;修正回路模型;误差改正;仿真

AbstractConsidering the unique superiority of airborne gravity survey，the application of gyro-stabilized platform in airborne gravity survey system was researched.Firstly，the stable loop system of single-axis gyro stabilized platform was established by using simulation module of matlab-simulink.Secondly，the mathematical module of correction circuit was established.Under the condition that we input limited parameters，simulation results were obtained.Thirdly，the horizontal error correction model for airborne gravity measurement was established and the horizontal error correction values were obtained.

Key words:airborne gravity measurement system;gyroscope-stabilized platform model;correction circuit module; horizontal error correction;simulation

1 引言

陀螺稳定平台是航空重力测量系统的重要组成部分。航空重力仪借助陀螺来保持重力仪本体的稳定取向，而不受飞机运动、基座倾斜和水平加速度的影响。现普遍采用自动控制的力平衡方法，也就是在外加干扰力矩作用时，设法产生一个与干扰力矩大小相等方向相反的力矩，以抵消外加干扰力矩对陀螺系统的影响，保持取定方向的稳定性。这种系统称陀螺稳定平台(下文简称平台)。

将陀螺安装在平台上，以控制平台方位，可以采用两自由度陀螺或单自由度陀螺。陀螺作为方位测量元件，加上放大器及执行机构(如转矩电机)组成闭路系统。单自由度陀螺所组成的平台方位控制系统分为两大类:直接稳定平台和间接稳定平台。在直接稳定系统中，采用陀螺力矩与外来力矩相平衡的方式，减小稳定对象的转动，达到方位稳定的目的。陀螺既用来测量客体角速度，亦用来产生陀螺力矩，构成力平衡反馈系统，这种系统的结构虽然简单，但往往需要选用特定的陀螺。在间接稳定系统中，陀螺直接反馈而作用于运动客体z轴的陀螺力矩相比外加力矩可忽略不计，因而不能直接稳定。系统的反馈回路由陀螺上角度转换器、放大器和力矩马达组成，由反馈力矩平衡输入力矩。如果在单自由度陀螺的稳定平台系统中增加加速度计，直接测得运动客体的加速度，积分后为运动速度，根据运动速度计算指示z轴的平台进动规律，可以保持平台与地理坐标系之间没有相对运动。

2 稳定回路

陀螺稳定平台系统由两部分组成:稳定回路和修正回路。稳定回路的设计目的是为了保证平台具有良好的动静态性能，以便在各种外干扰作用下都能向控制系统提供精确的惯导基准和使平台台体坐标系按照控制信号的需要达到给定的位置。图1为通过平台稳定回路工作原理画出的单轴陀螺稳定平台稳定回路系统示意图［6］，其中M为由于载体运动引起绕陀螺敏感轴的输入力矩，Mf为通过伺服电机输出的反馈力矩，Me绕陀螺敏感轴的输入力矩，α为平台在轴方向的输出姿态角，θ为陀螺的进动角，ein为平台控制器输出信号。

图1 单轴陀螺稳定平台稳定回路系统示意图Fig.1Sketch of stable loop system of single－axis gyro stabilized platform

双轴稳定平台采用两个单自由度陀螺仪或一个双自由度陀螺仪作为敏感元件。本文采用两个单自由度陀螺仪，由于两个方向的稳定回路设计几乎相同，先建立单轴稳定平台的系统(图1)和各部传递函数(表1)，其中JP为台体及其附件相对输出的转动惯量，H为陀螺仪角动量，J为浮子组合件绕输出轴的转动惯量，C为阻尼器系数，C2为比例系数，τ为积分时间系数。不考虑系统中比例系数。

表1 单轴稳定平台稳定回路系统传递函数Tab.1Transfer functions of stable loop system of singleaxis gyro stabilized platform

运用Matlab控制系统工具箱提供的SISO设计工具［4］，可以方便地进行稳定性分析和补偿器的设计。

海空重力测量要求稳定平台具有强抗干扰性。平台稳定回路要求在干扰力矩为14.7 Nm时，平台偏差角足够小，静态力矩刚度足够大。基于其特殊性，对超调量σ、调节时间tS和振荡次数N也作出规定:σ＜20%，tS＜0.25 s，N＜2。由已知参数得系统开环传递函数为

3 修正回路

惯导平台的修正回路的构成原理及作用:经过有害加速度补偿后的加速度信息一次积分得到的速度信息除以当地的地理曲率半径后得到载体相对于地球旋转的角速率，将该角速率信息加到陀螺仪的力矩器时相应的陀螺仪发生进动，进而使得力矩电机带动平台进行旋转，最后达到陀螺仪的信号器输出为零。这样，平台就完成了跟踪当地地理坐标系的功能。根据陀螺稳定平台运动学理论［1.2］，惯导系统的误差方程(状态方程)为

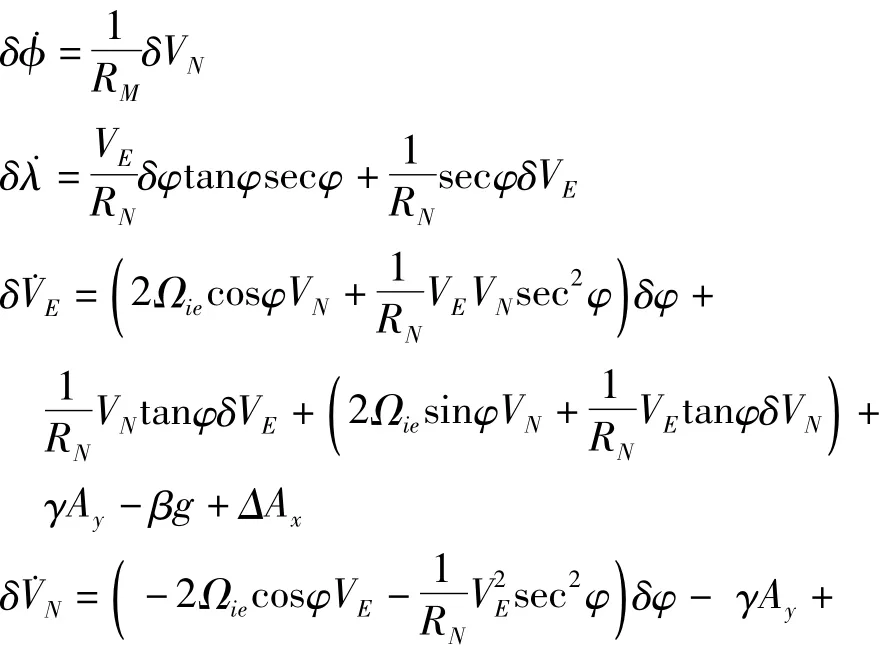
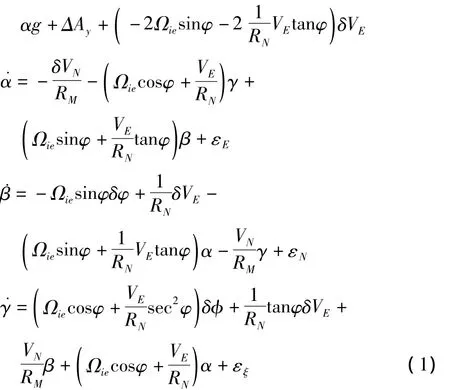
式中，α、β、γ为平台在东西、南北、垂直方向姿态角，VE、VN为载体水平方向速度，δVE、δVN为平台水平方向速度误差，φ、λ为纬度和经度，δφ、δλ为纬度误差和经度误差，εx、εy、εξ为陀螺漂移ΔAx、ΔAy为加速度计零偏，Ωie为地球自转角速度，当载体的运动速度较低时可忽略载体的运动，认为与静基座的情况相同。同时，认为地球为圆球体，即RM=RN=R。忽略垂直方向的姿态误差，则上式可简化为如下:

此即静态条件下稳定平台水平误差方程。在此基础上求系统特征根为:

因此，平台系统输出值以ωS和Ωiesinφ两种角频率形成的差拍，其中ωS为舒拉频率。Ωiesinφ为付科频率。为了消除周期震荡对平台的影响，进一步减小平台姿态角，加入阻尼网络是一种有效方法。

式(5)为加入阻尼网络的稳定平台水平误差方程。其中H为水平轴阻尼网络(假设两轴阻尼网络

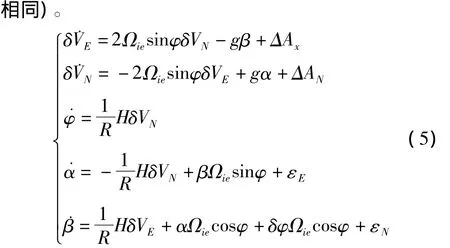
4 航空重力水平误差改正［6］

理论上当稳定平台准确模拟当地地理坐标系时，平台与水平面平行，重力仪对水平加速度不敏感。但由于陀螺漂移以及其他误差的存在，平台与水平面不平行，表现在稳定平台输出姿态角α、β上。以α为例(如图2，图中画阴影部分表示平台的倾斜方向，α为平台在X方向倾角，A为水平加速度，g为重力实际量，g'为重力仪敏感值)，可得:

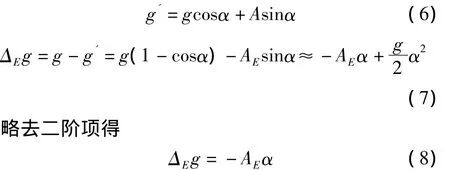
式中g为重力加速度，Δg为横向水平加速度改正，g'为重力仪敏感重力值，A为水平加速度，α为平台水平倾角。

同理可以得南北轴倾角的略去二阶项改正:

图2 平台水平倾角对重力测量值的影响Fig.2Influence of pitch on gravimetry results

5 仿真条件和仿真

陀螺稳定平台控制系统是连续系统，运用simulink工具箱进行建模。用sisotool工具进行系统稳定性分析，并选取系统校正网络。

系统参数设计为:JP=5×10－3kgm2，J=2.25 ×10－5kgm2，C=49.033 25 Nms，τ=0.000 45 s，H =5.23×106kgm2/s，τ1=0.007 7，τ2=0.000 14，假定电机传递系数为1。简化稳定回路传递函数为，依据式(2)、(5)可画出修正回路方块图如图3所示，仿真条件为:Ax=Ay=30 m/s2，ΔAx=ΔAy= 0.000 5 m/s2，dx=dy=0.005°/h，α0=β0=10″，δVx=δVy=0.05 m/s，φ=31.5°。其中阻尼网络选择为

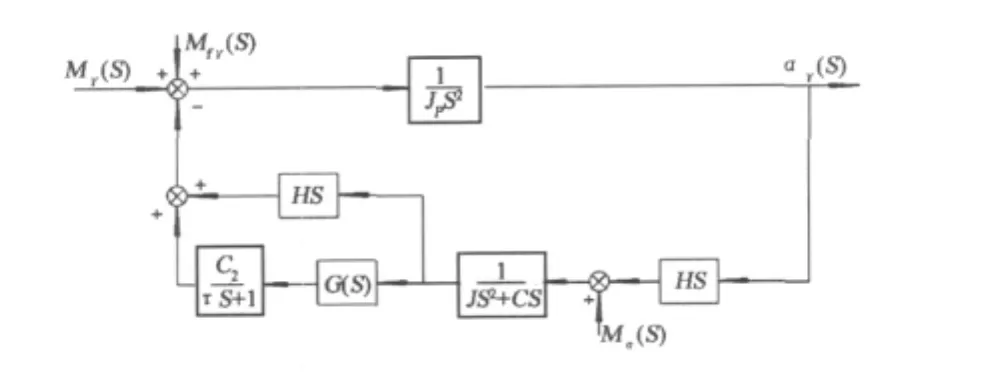
图3 单轴陀螺稳定平台稳定回路系统示意图Fig.3Sketch of stable loop system of single-axis gyro stabilized platform

6 结果分析

图4是无阻尼状态下平台水平误差角的仿真曲线。从图4可以看出:平台水平误差α、β角在无阻尼状态下都具有振荡传播特性，为了减小平台的水平误差对重力测量的影响，必须将振荡误差进行阻尼。图5是水平阻尼状态下平台误差α、β角的仿真曲线。可以看到，经过水平阻尼后，系统的水平误差在一段时间后趋于稳定。α稳定误差值大约为5.166×10－5rad，β的稳定误差值大约为5.069× 10－5rad。陀螺稳定平台系统经过水平阻尼后，不仅提高了水平误差角的精度，而且有效地抑制了误差振荡特性。

由图4、5可见，通过Simulink仿真图，可以直观地得到水平误差α、β角的变化趋势，并能够定量地确定各误差值变化量的大小，而且仿真结果的精度完全在要求的误差精度范围内。根据此结果，依式(8)、(9)对重力仪测量值采取相应补偿措施，就可以减小或消除稳定平台引起的重力仪测量误差。

图4 无阻尼平台误差输出α、βFig.4Simulation results(α，β)of the horizontal error output of stable platform in free damp state

图5 阻尼平台误差输出α、βFig.5Simulation results(α，β)of the horizontal error output of stable platform in level damp state

依据公式(8)、(9)得到阻尼网络下平台不平行引起的重力仪测量误差仿真图如图6所示，可知由平台不平行引起的重力仪测量误差稳态值为－2.91 ×10－5m/s2，可见水平误差改正的必要性。

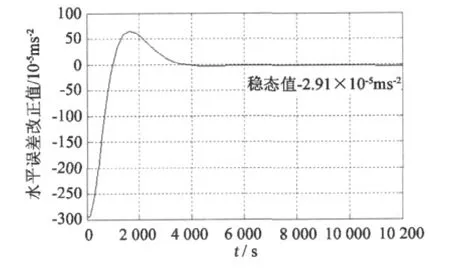
图6 阻尼网络下平台不平行引起的重力仪测量误差Fig.6Influence of unparallel between stable platform and local horizontal plane on gravimeter error in level damp state

7 结论

1)稳定回路是陀螺稳定平台的核心部分，其中校正网络的设计尤为关键，直接关系到陀螺稳定平台性能的优劣。

2)修正回路实现平台准确跟踪地理坐标系，其精度与平台精度正相关。通过加入合适的阻尼网络，可以有效地提高平台姿态角的精度，并消除周期震荡对平台的影响。

3)通过合理地设计陀螺稳定平台的稳定回路，准确地实现了修正回路，可以使平台姿态角达到航空重力测量10－5ms－2级的测量要求。

4)应用MatlabSimulink进行陀螺稳定平台系统设计、分析与仿真，不仅避免了应用高级语言进行仿真时的巨大工作量，而且改善了系统的性能指标，实现了系统的有效开发。

1Lowreys J and Shellenbarger J C.Passive navigation using inertial navigation sensors and maps［J］.Naval Engineers Journal，1997，109(3):245－249.

2Lin Zhao and Wei Gao.The experimental study on GPS/ INS/DVL integration for AUV［A］，Position location and navigation symposium，2004［C］.Orlando:Institute of Navigation，2004，337－340.

3赵立业，等.基于Simulink的高精度重力仪稳定平台水平误差仿真［J］.中国惯性技术学报，2007，15(2):147－150.(Zhao Liye，et al.Simulation of horizontal error of Simulink-based gravimeter stable platform［J］.Journal of Chinese Inertial Technology，2007，15(2):147－150)

4李钟慎.用sisotool实现经典控制系统的设计与仿真［J］.计算机仿真，2007，24(5):173－175.(Li Zhongshen.Design and simulation of classical control system using sisotool［J］.Computer Simulation 2007，24(5):173－175)

5邓正隆.惯性技术［M］.哈尔滨:哈尔滨工业大学出版社，2006.(Deng Zhenglong.Inertial technology［M］.Harbin: Harbin Institute of Technology Press，2006:93－146)

6张善言，等.航空重力仪的试验［J］.地球物理学报，1990，33(1):70－76.(Zhang Shanyan et al.Test of an airborne gravity meter［J］.Chinese Journal of Geophysics，1990，33(1):70－76)

7Verdun J and Klingelé E E.Airborne gravimetry using a trapped-down LaCoste and Romberg air/sea gravity meter system:a feasibility study［J］.Geophysical Prospecting，2005，53(1):91－101.

8Stelkens-Kobsch T.The airborne gravimeter Chekan-A at the Institute of Flight Guidance(IFF)［A］.Gravity，Geoid and Space Missions;GGSM 2004;IAG International Symposium［C］.Berlin，Heidelberg:Springer-Verlag，2006，129 (2): 113－118.

EMULATION BASED ON MATLAB-SIMULINK OF GYROSCOPESTABILIZED PLATFORM OF AIRBORNE GRAVIMETER

Wang Jin1，2)and Liu Lintao1)(
1)Key Laboratory of Dynamical Geodesy，Institute of Geodesy and Geophysics，CAS，Wuhan430077) 2)Graduate School of Chinese Academy of Science，Beijing 100049

P223+.4;V241

A

1671-5942(2011)03-0145-05

2010-12-09

国家自然科学基金(41074050)

王锦，男，1980年生，硕士，研究方向:航空重力测量系统陀螺稳定平台.E－mail:tywangjin@sohu.com