非线性模型的一阶偏导数确定方法及其在TLS精度评定中的应用*

孔建 姚宜斌 黄承猛

(武汉大学测绘学院，武汉430079)

非线性模型的一阶偏导数确定方法及其在TLS精度评定中的应用*

孔建 姚宜斌 黄承猛

(武汉大学测绘学院，武汉430079)

基于整体最小二乘(TLS)数据处理理论以及TLS迭代算法，利用泰勒公式确定非线性模型一阶偏导数，推导了其误差量级。并将该方法应用于TLS精度评定，提出了检验结果可靠性的方法，最后通过实验验证了该方法的可行性。

整体最小二乘;泰勒公式;一阶偏导数;可靠性检验;迭代算法

AbstractOn the basis of the total least-squares(TLS)data processing theory and an iterative algorithm for TLS，first-order partial derivative of the nonlinear model was determined by using Taylor formula and the error magnitude of the results was derivated.The method was applied to the TLS precision evaluation，and the method for reliability testing is proposed.The experimental results verify the feasibility of the method in TLS precision evaluation.

Key words:Total Least-Squares(TLS);Taylor formula;first-order partial derivative;reliability testing;iterative algorithm

1 引言

测量数据处理需要解决两方面的问题:一是要在某种估计准则下求出待估参数值;二是要评估出参数的精度。测量数据处理模型中函数模型表征了观测量与参数之间存在的客观联系。函数模型往往是线性的，这一方面是与测量上常用的最小二乘平差方法有关，另一方面，测量数据处理中误差传播定律建立在线性模型的基础上。对于非线性模型，测量上常采用线性化的方法，用函数的一阶偏导数项近似表达函数模型［1，2］。

设计矩阵含有误差下的平差问题在二维直线拟合模型中被多次提出，随后被命名为整体最小二乘(TLS)问题。TLS的思想最早可以追溯至20世纪初，但直到1980年才由Golub和Van Loan共同完成其数学结构的研究，给出了基于矩阵的奇异值分解第一个数值稳定的算法—SVD方法［1］。近十几年来，随着科学计算方法的发展，国内外学者对TLS的可解性理论进行了深入的研究，各种解算整体最小二乘问题的方法层出不穷，常见的有SVD方法、完全正交方法、Cholesky分解法、迭代解法等［3－8］。

但目前TLS解算的参数很难给出可靠的精度信息，这成为制约TLS进一步在测量数据处理中应用的瓶颈问题［9］。本文在迭代法求解参数估值的基础上，提出了待求参数关于观测量一阶偏导数确定策略，进而得到参数的精度信息，并通过实测算例验证了策略的可行性，得到了一些有意的结论。

2 TLS迭代算法

TLS数据处理模型为

这一模型类似于经典的间接平差模型，但与经典模型不同的是，这时的平差模型考虑了系数矩阵的误差。TLS问题求解的一种常用算法是迭代法［4］，迭代法的最大特点就是算法简单。这种方法以迭代方程

为基础建立。其中，Nb=E+^X^XT，L=(L1－d1L2－d2…Ln－dn)T，迭代过程可以按以下流程进行:

1)获取未知参数的初值X0;

2)根据观测值信息以及未知参数初值X0，取^B(0)=B，由式(2)求取未知参数的平差值^X(1);

3)根据Nb=E+^X^XT，求N(1)b=E+^X(1)^X(1)T;

4)根据求得的N(1)b、未知参数的平差值和观测值信息，由式(3)求取设计矩阵平差值^B(1);

5)重复2)～4)步，直到两次计算的参数值之差小于一定的域值，退出迭代，输出结果。

迭代编程实现简单，但是迭代法是对参数真值的逐步逼近，迭代方程往往非线性程度过高，给后续的精度评定带来了困难，所以探讨在迭代法基础上TLS精度评定问题是有意义的。

3 TLS精度评定

3.1 非线性模型一阶偏导数确定策略

复杂函数一阶偏导数项确定问题，在数学、光学、热力学等学科中经常碰，很多学者提出过各种算法［6，7］。本文在泰勒展开式的基础上，提出一种新的确定一阶偏导数的解析算法。设隐函数确定了Y与X1、X2…Xn之间的函数关系:

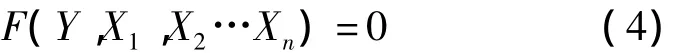
精度评定需要提取参数Y关于X1、X2…Xn观测量的线性信息，这种线性信息可以用参数Y关于观测量X1、X2…Xn的一阶偏导数来表示，即:

所以精度评定的问题转换成求取各项一阶偏导数问题。对于现有的TLS参数估计公式而言，如使用迭代法，求取各项偏导数的工作量很大。

泰勒公式是处理复杂数学函数的有效工具，式(6)给出了多元函数的泰勒公式展开(以二元为例)。

定理设z=f(x，y)在点(x0，y0)的某一领域内连续且有直到(n+1)阶的连续偏导数，(x0+h，y0+ k)为此领域内任一点，则有:

式(7)表明，对于多元函数如果在仅考虑单个自变量变化的情况下，它的泰勒级数展开式可以简化为一元函数的形式。

对既定的函数F(z，x，y)=0或z=f(x，y)而言，给定x=x1，y=y1，可以准确确定z1的值;在保持y =y1值不变的情况下，变化参数x=x1+h，得到相应z值z=z2，进而得到z值的变化量Δz=z2－z1。把结果代入式(7)可以看到，由于x的变化量h是已知的，z是由给定的函数准确确定，带回式(7)后得到的是一个包含n个未知数(n项偏导数)的方程。如果对x变化n个不同的h值，相应地可以得到n个方程，由于最后的拉格拉日余项很小，可忽略不计，那么从理论上而言，从得到的n个方程中可以解得相应的n项偏导数，解得的n项偏导数中就含有精度评定需要的一阶偏导数。如果对所有的自变量进行上述过程的处理，就可以用解析方法得到因变量关于各项自变量的偏导数。

从理论上，上面得到的方程可以解算出所有需要的偏导数，但实际计算过程会引入一些计算误差，一方面对于式(7)，实际计算不会考虑n阶导数，另一方面解算结果也会受到计算机计算精度的影响，因为所取的h往往是一个微小量，从而导致求解各项偏导数方程的系数矩阵(即式(12)中的矩阵N)近乎病态，使得计算的稳定性较差。为了提高解算的精度，采用牛顿法进行处理，首先，令x=x1+h、y =y1可以得到:

式中ε1表示没有考虑后面的高阶导数项，在此基础上，令x=x1－h、y=y1，可以得到:

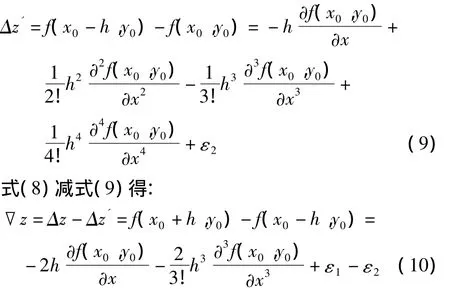
这是数值计算中构造迭代方程常用的方法，这样处理可以提高偏导数解算的精度，这一点可以从下面误差项推导的结果中看到，在式(10)中虽然偏导数只写了两项，但是结果却是考虑的4阶偏导数的效果，通过实验可以发现，这样处理比直接使用式(7)计算得到的结果更加稳定。

实际计算中，式(10)最后的误差项ε1－ε2是直接忽略掉的，下面讨论忽略项ε1－ε2对最后结果的影响以及在使用上述方法计算一阶偏导数时考虑求解阶数与最后估计结果精度之间的关系，从而分析ε1－ε2对估计结果的影响。为了表达上的直观，对x所取的变化量h在推导中用Δx表示。

将N的行列式带入，用Δf1、Δf2分别表示忽略ε1－ε2而造成的估计一阶，二阶偏导数的误差，可以得到Δf1、Δf2的具体形式:

因为x的变化量Δx，z的变化量Δz是准确已知不含误差的，在不考虑计算机计算精度的情况下，Δf1、Δf2就是用上面原理计算所产生的计算误差。从公式(18)可以看到:

1)在模型5阶偏导数不为零的情况下，取Δx在10－3数量级，则Δf1计算误差在10－12数量级，Δf2的计算误差在10－6数量级。如果考虑ε1－ε2七阶导数以后的项，对Δf1、Δf2的影响可以在5阶项对其影响的基础上再乘以Δx2，更高阶项的影响依次类推，数量级会更小，可见在推导时仅考虑ε1－ε25阶项是合理的。

2)从结果中可以看到，计算得到的Δf1远比Δf2量级要小，即求得的偏导数精度依次下降，一阶偏导数精度最高。

3)从计算结果可以看到Δf1的量级很小，如果再添加一阶偏导数，仍取Δx在10－3数量级，Δf1量级会到10－20，甚至更小。

3.2 TLS精度评定及可靠性分析

由于得到的一阶偏导数对最后参数精度评定结果有直接的影响，所以评定所得结果的可靠性显得尤为重要。首先，由于参数估值满足迭代方程的第一式:

在迭代退出时，所得参数估值、系数矩阵平差值满足式(19)，符合的程度和迭代推出的条件有关。由式(19)可以得:

参数估值关于观测向量L的偏导数可以由式(20)得到。所以可以通过求得的参数关于观测向量的一阶导数值与式(20)得到的一阶导数值做差进行比较，用以检测得到的偏导数的可靠性。

由于没有考虑到式(4)的约束，式(20)求得的偏导数是不严密的，所以这一可靠性评定方法只能作为估计可靠性的一种参考。探测偏导数计算过程中是否含有粗差，本文将在算例部分进行说明。

4 算例分析

实验数据采用某地变形监测的实测数据，观测数据为某河流沿岸观测点的水位值、温度值，以及位移量，拟合模型如下:

其中S为位移量，h为水位值，t为温度值，a、b为待拟合的参数。采用5组观测数据进行拟合，用TLS原理采用迭代法计算得到参数值，这里直接给出:a =0.559 6，b=－0.129 9。

偏导数拟合实验采用二阶拟合，表1列出的是二阶拟合得到的各项一阶偏导数值，由于篇幅所限，仅列出参数a对15个观测量的偏导数。表2列出的是按公式(19)计算得到的参数关于观测向量的偏导数值，表中所列较差项是拟合值与按式(20)计算值之差。

表1 一阶偏导数拟合值(单位:m)Tab.1Fitted values of first-order partial derivative(unit: m)

表2 一阶偏导数计算值(单位:m)Tab.2Calculated values of first-order partial derivative (unit:m)

从表2所列的较差项中，可以看到两种计算方法的结果最大不符值达到13 mm。本文进行所求偏导数可靠性估计时，并不把按式(20)得到的计算值当作真值，这是因为式(20)是在没有考虑式(3)的基础上得到的，计算结果是不严密的，仅能作为探测拟合值是否含有粗差的依据，这一点可以用下面的实验说明。

用两种方法得到的偏导数，做下面的预报实验，并对结果进行对比。对上面不符较大的观测量取扰动Δx，用式(21)进行参数值变化的预报:

将两种方法得到的偏导数分别带入式(21)进行预报，将得到的结果与参数的真实变化进行比较(表3)，实验中选择的5组数据分别是表2中较差较大的1

表3 不同方法得到的偏导数预报值(单位:m)Tab.3Forecast values with different methods(unit:m)

从表3可以看到，用式(20)计算得到的偏导数进行预报的结果没有拟合得到偏导数的预报结果精度高。所以在实际操作中，用计算的偏导数进行偏导数可靠性检验时，只能检验拟合的结果中是否含有较大的拟合偏差，防止拟合过程中发生错误。

另外，在采用上述原理进行偏导数估计时，观测量的扰动取多大量级，应该由观测量自身精度所决定，应该和观测量自身的误差相匹配，这样求得的偏导数用以精度评定是比较合理的。

表4中列出的是对迭代法求解参数精度评定的结果。为了便于比较，表中列出了用经典最小二乘方法求解得到的参数值以及精度。

表4 参数精度(单位:m)Tab.4Accuracies of parameters(unit:m)

从表4中可以看到，TLS和LS得到的参数精度相当，这是因为两种算法求解参数的精度和观测值的误差分布和观测值数目有关，在观测精度较好的情况下，两种解法的参数精度相当;但在观测值精度较差的境况下，两种算法会出现较大偏差［7］。另一方面，LS参数的协因数阵由法方程系数矩阵N求拟得到的，而N是由设计矩阵得到的，在设计矩阵B含有误差的情况下，LS的精度没有考虑到B中所含有的误差，所以LS评定得到的只是参数的一个伪精度，表4中第3行给出了用设计矩阵平差值评定的LS参数的实际精度。

5 结论

在TLS迭代法的基础上，推导了一种精度评定策略，并通过实验验证了算法的正确性，以及精度评定策略的可行性。从程序实现的角度来看，在已有的参数估计代码基础上，这种精度评定策略便于编程实现。

本文提供的TLS精度评定数值解法，完善了TLS精度评定理论上的缺陷，使TLS具有了工程实践应用的理论基础，对TLS的推广应用是有意义的。

1武汉大学测绘学院测量平差学科组.误差理论与测量平差基础［M］.武汉:武汉大学出版社，2003.(Survey Adjustment Disciplane Unit of Surveying and Mapping College of Wuhan University.Error theory and measure of the basis adjustment［M］.Wuhan:Wuhan University Press，2003)

2邱卫宁，等.测量数据处理理论与方法［M］.武汉:武汉大学出版社，2008.(Qiu Weining，et al.The theory and method of surveying data processing［M］.Wuhan:Wuhan University Press，2008)

3Musheng Wei.Algebraic relations between the total least squares and least squares problems with more than one solution［J］.Numer.Math.，1992，62:123－148.

4孔建，姚宜斌，吴寒.整体最小二乘的迭代解法［J］.武汉大学学报(信息科学版)，2010，35(6):711－714.(Kong Jian，Yao Yibin and Wu Han.Intervative method for total least-squares［J］.Geomatics and Information Science of Wuhan University，2010，35(6):711－714)

5Sabine Van Huffel and Hongyuan Zha.The total least squares problem.Handbook of Statistics［J］.Handbook of Statistics，1993，9:377－408.

6Michael Krystek and Mathias Anton.A weighted total leastsquares algorithm for fitting a straight line［J］.Meas.Sci.Technol.，2007，18:3438–3442.

7Burkhard Schaffrin.Total least-sqares(TLS)for geodetic straight-line and plane adjustment［J］.Anno lxv Bollettino Di Geodesiae Scienze Affinin，200，3:141－166.

8Akyilmaz O.Total least squares solution of coordinate transformation［J］.Survey Review，2007，(1):68－80.

9Jiangqing cai and Erik W Grafarend.Systematical analysis of thetransformationbetweenGauss-Krueger-Coordinate/ DHDN and UTM-Coordinate/ETRS89 in Baden-Wurttemberg with different estimation methods［J］.Geodetic Reference Frames，International Association of Geodesy Symposia，134:205－211.

METHOD FOR DETERMINING FIRST-ORDERPARTIAL DERIVATIVE OF NONLINEAR MODEL AND ITS APPLICATION IN TLS ACCURACY ASSESSMENT

Kong Jian，Yao Yibin and Huang Chengmeng
(School of Geodesy and Geomatics of Wuhan University，Wuhan430079)

P207

A

1671-5942(2011)03-0110-05

2011-01-23

国家自然科学基金(40774008，40721001);中央高校基本科研业务专项

孔建，男，1987年生，硕士生，主要从事测量数据处理理论与方法研究.E－mail:liuhukj@163.com