泥岩渗流-应力耦合蠕变损伤模型研究(Ⅰ):理论模型

贾善坡 ，陈卫忠 ，于洪丹，李香玲

（1. 长江大学 城市建设学院，湖北 荆州 434023；2. 山东大学 岩土与结构工程研究中心，济南 250061；3. 中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室，武汉 430071；4. Euridice, SCK·CEN, 比利时 摩尔 2400）

1 引 言

对于软岩工程问题，流变学的研究非常重要，一方面是由于软岩工程岩体本身的结构和组成反映出明显的流变性质；另一方面也是由于长期受力使流变性质更为突出。大量的现场量测和室内试验都表明，对于软弱岩石以及含有泥质充填物和夹层破碎带的松散岩体，其流变属性则十分显著[1]。

地下工程围岩在受到工程扰动和环境变动之后，由于围岩内部存在微裂隙，其蠕变过程往往是一个内部组织结构不断发生变化、调整的非线性过程，必将带来能量的耗散，使耗散能密度不断增大，损伤逐渐积累，故蠕变过程是一个不可逆热力学过程。缪协兴[2]基于大量试验研究，建立了以能描述损伤历史的蠕变模量为参数的岩石蠕变损伤方程，由该方程能方便地确定出任一时刻的损伤状态。金丰年[3]从损伤角度研究岩石在拉压作用下变形破坏的非线性特性，基于割线模量法定义损伤变量，建立岩石非线性流变损伤本构方程。何开胜[4]根据黏土的微观变形机制，建立了描述结构性黏土变形的弹黏塑性损伤模型，并通过实例验证了该模型能够较好地反映黏土的加载变形、固结变形和蠕变变形。陈沅江[5]从内时理论出发，通过在内蕴时间中引入牛顿时间，在Helmholtz 自由能中引入损伤变量，利用连续介质不可逆热力学的基本原理推导了软岩的内时流变本构方程。范庆忠[6]指出软岩蠕变过程中微观结构会发生变化，并导致软岩形变行为产生相应的改变，引入非线性损伤、硬化变量代替Burgers模型中的线性损伤、硬化变量，可以反映这种改变对软岩蠕变的影响，建立了非线性蠕变模型，可以描述软岩蠕变过程3个阶段的变形特征。陈卫忠[7]根据流变、低渗透率及损伤自我恢复等特性，结合金坛储气库盐岩三轴蠕变的研究成果，建立盐岩三维蠕变损伤的本构方程和损伤演化方程。王芝银[8]提出了流变位移的反演模型以及岩体多场耦合流变模型。

核废料的安全处置不仅关系到核电、核工业的可持续发展，而且也关系到人类生存环境和地球的保护。因此，世界许多有核国家都倾入大量人力、巨资开展核废料处置研究工作。泥岩由于其低渗透性、良好的蠕变性和遇水损伤自修复的特性，被认为是储存核废料的备选场地之一。在比利时，第三系 Boom泥岩层被选作处置高放废物的场址，在Mol场地 223 m深的泥岩建造中建设了地下实验室，论证处置高放废物的可行性[9－10]。本文以Boom Clay泥岩为研究对象，根据室内和现场监测成果，提出一个能反映泥岩蠕变全过程的泥岩蠕变损伤本构关系，并且考虑蠕变过程中渗流-应力的耦合作用。本文的第Ⅰ部分详细介绍建议模型的基本公式；对于数值算法、模型参数的确定以及工程应用将在第Ⅱ部分中给出。

2 Boom Clay泥岩蠕变损伤特性分析

Boom Clay泥岩非线性很强，在变形很小时就会产生塑性，塑性和流变同时产生，目前还没有很好的本构模型来描述其力学特性。

2.1 室内蠕变试验分析

试件尺寸和相关参数如表1所示。

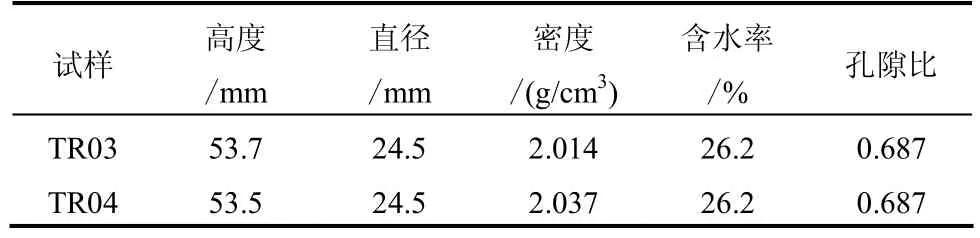
表1 室内蠕变试验试件尺寸及相关参数Table 1 Geometry, initial water content and void ratio for the specimens tested

在排水条件下，对泥岩试样进行在偏应力状态下的蠕变试验[1]，试验流程如下：①加载围压p到2.5 MPa，加载速率10-5MPa/s；②首次施加偏应力q，施加到1 MPa；③保持应力不变，持续时间为10 d；④第2次施加偏应力，TR03增加到1.5 MPa，TR04增加2 MPa。

对试样TR03和TR04进行室内蠕变试验，轴向、径向和体积应变如图1、2所示。可以看出，当偏应力q小于1 MPa时，泥岩几乎不发生蠕变现象；试样TR03在偏应力q达到1.5 MPa时，出现较为明显的蠕变现象，由于试验故障，该阶段的蠕变持续时间较短；试样TR04在偏应力q达到1 MPa时，开始出现蠕变现象，但是蠕变现象不明显，当偏应力q达到2 MPa时，出现较为明显的蠕变现象，该级载荷施加约8 d后，蠕变由衰减蠕变阶段进入到稳态蠕变阶段。

从这两个试验可以发现，在围压p为2.5 MPa，偏应力q小于1.0 MPa时，蠕变现象不明显，初期蠕变与稳态蠕变的界限约为1.5～2.0 MPa。

图1 TR03在不同偏应力下的蠕变曲线Fig.1 Results of creep test TR03

图2 TR04在不同偏应力下的蠕变曲线Fig.2 Results of creep test TR04

2.2 现场长期变形监测

长期变形监测主要布置在Test drift以及后期建设的Shaft02的衬砌变形[1]。

Test drift水平巷道的监测数据非常具有代表性，在衬砌编号为R15、R29、R43、R71、R83以及R105等位置布置了测点，连续监测了近20年，其收敛变形如图3所示，衬砌支护后，前2年内衬砌变形迅速增加，随着时间的延长，衬砌的变形逐渐增大，并趋于平缓，18年后R15环的直径收缩量约为 8 cm，而 R83和 R105环的直径收缩量约为6 cm，可见，蠕变近20年后衬砌的收缩量约为6～8 cm。

Shaft02监测的部位主要分布在竖井和connecting gallery交叉的位置，衬砌的变形较大，变形随着时间的增长逐渐增大，最大值约为15 cm，可见泥岩的蠕变效应非常明显。

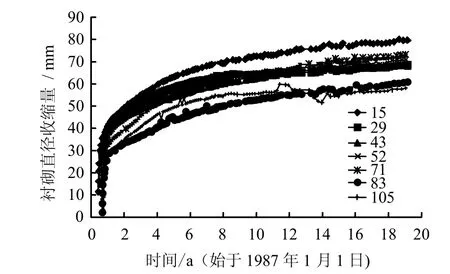
图3 Test drift衬砌直径收缩量随时间的变化Fig.3 Lining convergence of test drifts with time in 20 years

3 基于 Mohr-Coulomb准则的泥岩蠕变本构关系

经过对Boom Clay泥岩室内三轴试验研究，认为Mohr-Coulomb准则能较好地反映该泥岩的弹塑性力学行为，因此，泥岩蠕变本构关系是基于Mohr-Coulomb准则而构建的。定义基于Mohr-Coulomb准则的蠕变势函数为

式中：c、ϕ分别表示黏聚力和膨胀角；σm=为平均应力；为等效应力；J2为应力偏量第二不变量，θ为Lode角，K(θ)为Mohr-Coulomb准则的修正变量，具体见文献[10]。

图4 蠕变等势面及其蠕变区域的定义Fig.4 Equivalent creep stress defined as the shear stress

对岩土材料的黏塑性模型而言，做如下假设：假定存在应力点的蠕变等倾面，该等倾面具有相同的“蠕变强度”，并由等效应力来确定；当材料发生屈服时，等效蠕变面与屈服面一致，在未发生屈服时，等效蠕变面由屈服面等比例缩小得到。在子午面上蠕变面与屈服面平行，在π平面上两者的截线也是平行的，蠕变面与屈服面的关系如图4所示，可以看出，在子午面上存在一锥形空间，在该空间内没有蠕变，因为该空间内的等效蠕变应力为0。

同塑性势函数一样，蠕变势函数为光滑连续的曲线，可以保证蠕变流动方向惟一，蠕变流动准则可由蠕变势函数得到，即

蠕应变张量dεc明显与应力σ有关，fcr的定义如下：

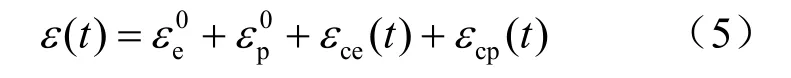
4 泥岩非线性蠕变损伤模型与损伤演化方程

对地下工程而言，由于开挖扰动区内部存在微裂隙，其蠕变过程往往是一个内部组织结构不断发生变化、调整的非线性过程，必将带来能量的耗散，损伤逐渐积累。通过引入损伤变量描述岩石的蠕变[6,11－15]，本文认为，泥岩的蠕变损伤是内部新裂纹产生和不断扩展的结果，是变形损伤与时间损伤效应的耦合。

4.1 泥岩蠕变损伤模型

泥岩的弹塑性变形相对于蠕变变形来说很小，蠕变损伤是泥岩在蠕变变形过程中发生的不可逆损伤，损伤变量是随着时间逐渐变化的。瞬态蠕变阶段持续的时间较短，并且变形量也较小，该阶段的蠕变损伤也比较小。

在一维条件下岩体的蠕变可以表示为

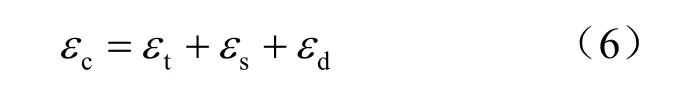
式中：εc为总蠕变；εt为瞬态蠕变；εs为稳态蠕变，εd为损伤引起的蠕变。

泥岩损伤蠕变可以定义为[11]

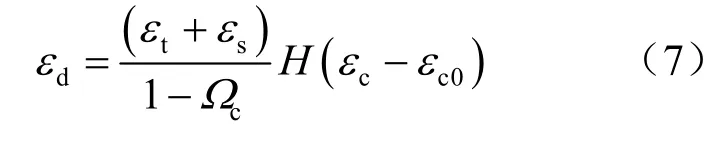
式中：Ωc为蠕变损伤；H为Heaviside函数；εc0为出现蠕变损伤的蠕应变阀值。且有：

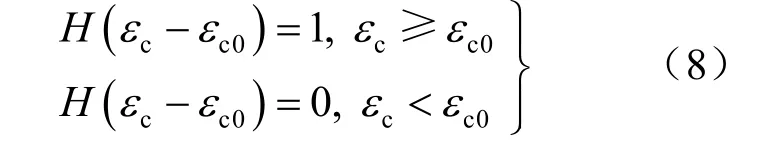
若认为在初始蠕变阶段即出现损伤，即εc0≈ 0，则损伤蠕应变可以简化为：

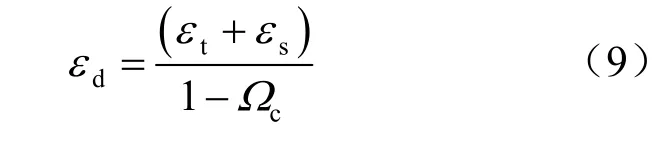
试验结果也表明：泥岩的蠕变速率不仅与时间相关，而且还与累积蠕变变形密切相关，非线性蠕变是其内部结构在蠕变过程中的综合表现，非线性蠕变损伤机制可更好地解释泥岩蠕变过程中所显现的非线性变形特征。考虑累积蠕变的非线性蠕变模型可表示为

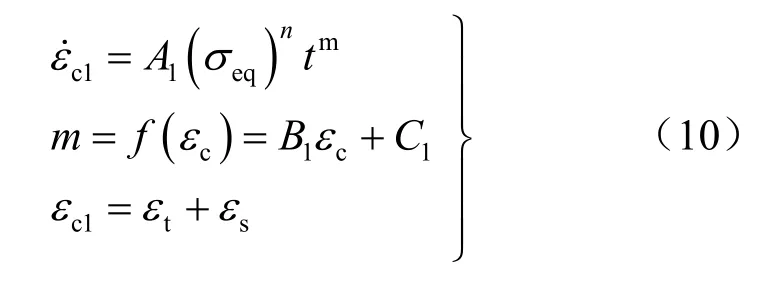
式中：A1、n、m、B1和C1为材料参数；m用于反映蠕变率的大小和变化情况，当 -1 ＜ m ＜ 0时，发生衰减蠕变；m=0时发生稳态蠕变；当m＞0可用于描述发生加速蠕变，m是累积蠕应变εc的函数，εc值越大，表明蠕变速度越高。

考虑到蠕变损伤，泥岩非线性蠕变损伤模型可表示为

从式（11）可发现，本模型共有4个未知参数，即 A1、n、B1和C1。

4.2 蠕变损伤演化方程

假定泥岩的损伤为各向同性时，可以推导出一维条件下的蠕变损伤变量[16]，即

式中：εc0为开始出现蠕变损伤的初始蠕变值，εc为总蠕变值。

可以认为，在 εc＜εc0时，泥岩的蠕变损伤为0；当 εc≥ εc0时，蠕变损伤迅速增大，直到泥岩破坏为止。图5给出了泥岩的蠕变损伤与蠕应变之间的变化曲线。

在三维条件下，假设泥岩的蠕变损伤为各向同性损伤，这样损伤变量可以用标量来描述。泥岩蠕变过程中的总损伤ΩT包括开挖卸载损伤Ω和蠕变变形过程中产生的蠕变损伤Ωc，即

其中，开挖卸载损伤Ω的计算模型和演化方程详见文献[10]。

将式（12）描述的一维蠕变损伤演化方程推广到三维情况，类似于等效塑性应变的概念，引入等效蠕应变具体计算公式为

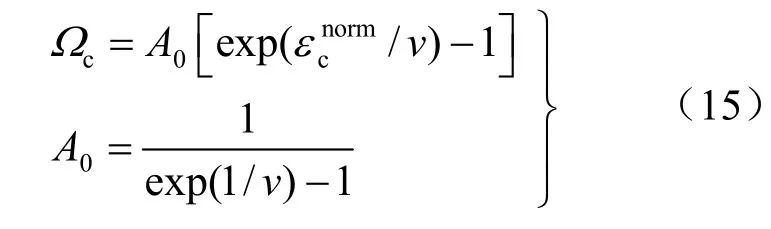
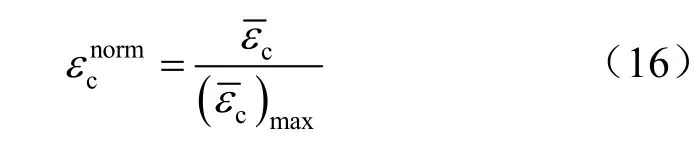
图5 泥岩蠕变损伤-等效蠕应变的变化曲线Fig.5 Relation curves between creep damage and normalized parameter of equivalent creep strain for different values of v

由图5可知，在v值较小时，在开始阶段，损伤增长较慢，此后随着蠕应变的增大，损伤迅速增大；而当v接近1时，蠕变损伤与等效蠕应变基本上呈线性关系。

5 泥岩蠕变过程中渗透性演化方程

Boom Clay泥岩巷道开挖扰动区渗透性演化主要包括两个过程：①开挖导致的围岩损伤、开裂和局部化断裂引起的渗透性增加；②支护后，由于裂隙的自愈合效应导致围岩的渗透性减小。

开挖引起应力重分布，原有裂隙的张开、扩大以及新破坏裂隙的形成，使其渗透性显著提高，泥岩的渗透性演化方程可以描述为[1]

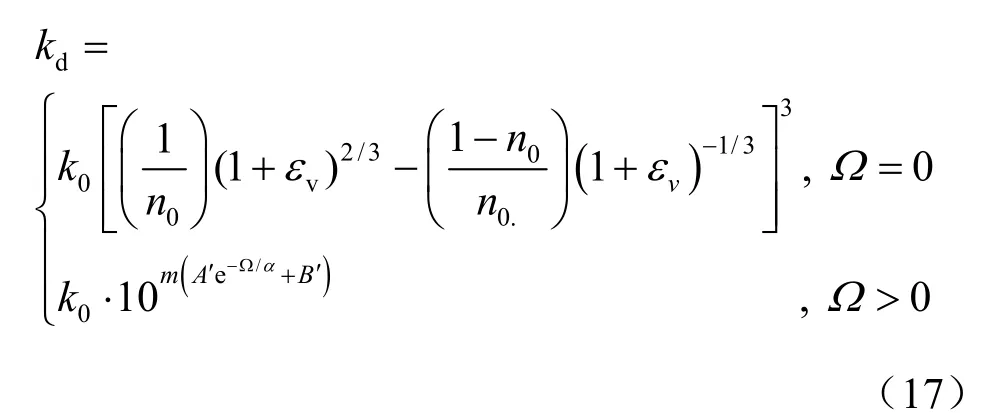
式中：k0和n0分别为未损伤泥岩的渗透率和孔隙度；εv为体积应变；m为泥岩破裂时渗透系数升高的数量级；Ω为开挖施工导致的损伤；α为材料参数，可通过试验确定；

孔隙度演化方程可以描述为[1]

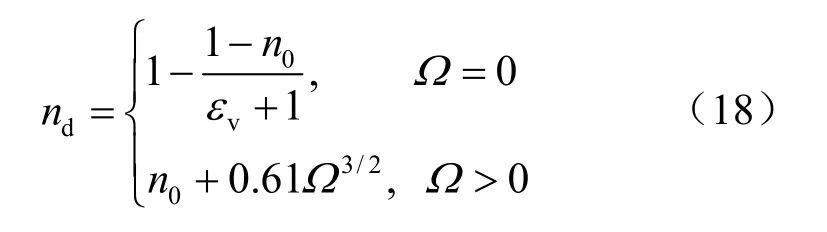
对Boom Clay泥岩而言，现场和室内试验均证明：微裂隙闭合或自愈合现象非常明显，裂隙的闭合与应力状态、固结以及蠕变等有关；在蠕变固结阶段，由于化学作用裂隙在孔隙水的作用下会发生闭合，裂隙的自愈合引起泥岩的渗透性和孔隙度发生一定程度的恢复，但不会使损伤发生恢复。

裂隙的自愈合机制涉及许多因素，主要由泥岩组成成分与孔隙水之间的化学相互作用引起的，而从力学的角度来说，影响的主要因素是围压和孔隙水，即有效围压越大、饱水时间越长，裂隙越容易自愈合。

通过比利时泥岩渗透性试验及相关研究可知，围压越大，裂隙越容易闭合和愈合[1]，定义愈合应力σheal来描述应力状态对裂隙闭合和愈合的影响，愈合应力σheal可表示为

式中：a1、a2为常数，本文主要研究在223 m处泥岩的水-力耦合行为，取a2=5 MPa，为前期固结压力；a1用于反映围压效应对愈合应力的影响，取a1=1；σeq为围岩Mises应力；用于表明σeq对于裂隙愈合的削弱作用。

从式（19）可知，当 σheal≥ 0时才会发生裂隙闭合和愈合现象；而当σheal＜0时不会发生裂隙自愈合现象。在隧道支护后，σ1越大（压应力），愈合应力就越大，有利于裂隙的闭合；而有效应力σeq越大，就越小，愈合应力就小，不利于裂隙的愈合。

巷道支护后，在饱和状态下孔隙水使得泥岩裂隙发生化学效应产生愈合现象，定义水化学愈合因子cheal来描述泥岩愈合的化学特性。在一定围压下，随着时间的增长，裂隙逐渐愈合，愈合因子cheal的表达式为

式中：a3为待定参数。

引入愈合因子h来描述围岩裂隙的自愈合性质，裂隙的愈合程度与围压以及水的化学作用有关。泥岩渗透性愈合因子h是愈合应力σheal和水化学愈合因子cheal的函数，愈合应力σheal越大，愈合因子h越小；水化学愈合因子cheal越大，愈合因子也越大。愈合因子h定义为

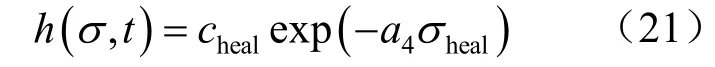
式中：a4为待定参数。

在泥岩巷道支护后，渗透性和孔隙度的演化方程可以表述为

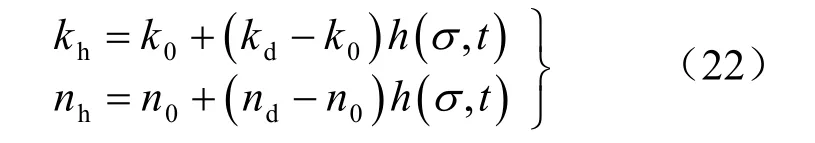
从渗透性演化方程可以发现，愈合应力越大，泥岩的渗透性越小；时间越长，泥岩的渗透性越小。

6 结 论

（1）泥岩的弹塑性变形相对于蠕变变形来说很小，瞬态蠕变阶段持续的时间较短，变形量较小；泥岩的蠕变速率不仅与应力水平、时间相关，而且还与累积蠕变变形密切相关，蠕变损伤变量随着时间逐渐变化，非线性蠕变损伤机制可较好地解释泥岩蠕变过程中所显现的非线性变形特征。

（2）泥岩围岩渗透性演化包括两个过程：开挖导致的围岩损伤、开裂和局部化断裂引起的渗透性增加；巷道支护后由于裂隙的自愈合效应导致围岩的渗透性减小。研究结果表明，围压、孔隙水和饱水时间是影响泥岩裂隙自愈合的主要因素。

（3）本文建立的蠕变损伤模型能够很好地反映泥岩蠕变过程中的衰减蠕变阶段、稳态蠕变阶段和加速蠕变阶段，且材料常数较少，便于从试验数据中获得。

本文的第Ⅱ部分将详细介绍蠕变损伤模型求解的有限元方程、数值实现方法、模型参数确定的反演方法以及在地下工程分析中的应用。

[1]贾善坡. Boom Clay泥岩渗流应力损伤耦合流变模型、参数反演与工程应用[D]. 武汉: 中国科学院武汉岩土力学研究所, 2009.

[2]缪协兴, 陈至达. 岩石材料的一种蠕变损伤方程[J]. 固体力学学报, 1995, 16(4): 343－346.MIAO Xie-xing, CHEN Zhi-da. A creep damage equation for rocks[J]. Acta Mechanica Solida Sinica, 1995, 16(4):343－346.

[3]金丰年, 范华林. 岩石的非线性流变损伤模型及其应用研究[J]. 解放军理工大学学报, 2000, 1(3): 1－5.JIN Feng-nian, FAN Hua-lin. Study of nonlinear rheology damage property of rock[J]. Journal of PLA University of Science and Technology, 2000, 1(3): 1－5.

[4]何开胜, 沈珠江. 结构性粘土的弹粘塑损伤模型[J]. 水利水运工程学报, 2002, (4): 7－13.HE Kai-sheng, SHEN Zhu-jiang. Elasto-viscoplastic damage model for structural clays[J]. Hydro-Science and Engineering, 2002, (4): 7－13.

[5]陈沅江, 潘长良, 曹平, 等. 基于内时理论的软岩流变本构模型[J]. 中国有色金属学报, 2003, 13(3): 735－742.CHEN Yuan-jiang, PAN Chang-liang, CAO Ping, et al.Endochronic rheological constitutive model of soft rock[J]. The Chinese Journal of Nonferrous Metals,2003, 13(3): 735－742.

[6]范庆忠, 高延法, 崔希海, 等. 软岩非线性蠕变模型研究[J]. 岩土工程学报, 2007, 29(4): 505－509.FAN Qing-zhong, GAO Yan-fa, CUI Xi-hai, et al. Study on nonlinear creep model of soft rock[J]. Chinese Journal of Geotechnical Engineering, 2007, 29(4): 505－509.

[7]陈卫忠, 王者超, 伍国军, 等. 盐岩非线性蠕变损伤本构模型及其工程应用[J]. 岩石力学与工程学报, 2007,26(3): 467－472.CHEN Wei-zhong, WANG Zhe-chao, WU Guo-jun, et al.Nonlinear creep damage constitutive model of rock salt and its application to engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 467－472.

[8]王芝银, 李云鹏. 岩体流变理论及其数值模拟[M]. 北京: 科学出版社, 2008.

[9]贾善坡, 陈卫忠, 于洪丹, 等. 泥岩隧道施工过程中渗流场与应力场全耦合损伤模型研究[J]. 岩土力学, 2009,30(1): 19－26.JIA Shan-po, CHEN Wei-zhong, YU Hong-dan, et al.Research on seepage-stress coupling damage model of Boom clay during tunneling[J]. Rock and Soil Mechanics, 2009, 30(1): 19－26.

[10]贾善坡, 陈卫忠, 于洪丹, 等. 泥岩弹塑性损伤本构模型及其参数辨识[J]. 岩土力学, 2009, 30(12): 3607－3614.JIA Shan-po, CHEN Wei-zhong, YU Hong-dan, et al.Parameter identification of new elastoplastic damage constitutive model for claystone[J]. Rock and Soil Mechanics, 2009, 30(12): 3607－3614.

[11]杨春和, 陈锋, 曾义金. 盐岩蠕变损伤关系研究[J]. 岩石力学与工程学报, 2002, 21(11): 1602－1604.YANG Chun-he, CHEN Feng, ZENG Yi-jin.Investigation on creep damage constitutive theory of salt rock[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(11): 1602－1604.

[12]徐卫亚, 周家文, 杨圣奇, 等. 绿片岩蠕变损伤本构关系研究[J]. 岩石力学与工程学报, 2006, 25(增刊 1):3093－3096.XU Wei-ya, ZHOU Jia-wen, YANG Sheng-qi, et al. Study on creep damage constitutive relation of greenschist specimen[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(Supp.1): 3093－3096.

[13]秦跃平, 王林, 孙文标, 等. 岩石损伤流变理论模型研究[J]. 岩石力学与工程学报, 2002, 21(增刊2): 2291－2295.QIN Yue-ping, WANG Lin, SUN Wen-biao, et al. Study on rheological theory model of rock damage[J]. Chinese Journal of Rock Mechanics and Engineering, 2002,21(Supp.2): 2291－2295.

[14]潘长良, 陈沅江, 曹平, 等. 岩石蠕变过程的不可逆热力学分析[J]. 中南工业大学学报, 2002, 33(5): 441－444.PAN Chang-liang, CHEN Yuan-jiang, CAO Ping, et al.Analysis of rock creep by means of irreversible thermodynamics[J]. Journal of Central South University of Technology, 2002, 33(5): 441－444.

[15]任建喜. 单轴压缩岩石蠕变损伤扩展细观机理CT实时试验[J]. 水利学报, 2002, (1): 10－15.REN Jian-xi. CT real-time testing on mesomechanism of creep damage propagation in rock under uniaxial compression[J]. Journal of Hydraulic Engineering,2002, (1): 10－15.

[16]谢和平. 岩石、混凝土损伤力学[M]. 徐州: 中国矿业大学出版社, 1990.