饱和黏土不排水剪切的热破坏
2011-09-20姚仰平杨一帆
姚仰平,万 征,杨一帆,牛 雷
(北京航空航天大学 交通科学与工程学院,北京 100191)
1 引 言
已有数据表明:温度升高会改变岩土体的应力重分布,进而导致岩土体的变形,当土体应力减小到不足以平衡外载荷时便会产生破坏现象。这种在外部荷载保持不变而由于温度变化所诱发的破坏可称之为热破坏现象。受温度影响的地下岩土结构广泛地存在于各种地下设施中,如热交换桩以及地下核废料掩埋装置等等。因此,研究温度变化对于岩土的应力-应变关系的影响规律尤其重要。国外学者对热破坏现象进行了大量研究工作。Baldi[1]早在1988年就对热破坏现象的细观机制进行了解释说明。Bourros[2]从变温对于饱和黏土的抗剪强度的影响角度进行了相应的研究,此后,Jefferson[3]也对饱和黏土的不排水抗剪强度在变温条件下进行了相关研究。Hueckel[4]等对正常固结黏土以及超固结黏土在不排水变温条件下的应力-应变特性进行了比较系统的试验研究。
Hueckel针对饱和正常固结 Boom黏土开展了升温下的三轴压缩不排水试验工作。等向固结压力值为5.75 MPa,试验结果如图1、2所示。为考查温度变化对于变形以及强度的影响,采用了对比试验,将饱和Boom黏土重复做了两次试验,第1次是固定常温下的常规不排水试验;第2次是常温加载到一定值,然后做常载升温试验。图1、2中圆圈表示在室温21 °C下所做的关于饱和正常固结土的不排水三轴压缩试验结果,而正方形表示了加载-升温的试验结果,在偏应力值达到2 MPa之前,保持温度在21 °C下做不排水三轴压缩加载试验;当偏应力值达到2 MPa时,保持外载不变,此时将温度由21°C升高到92 °C。由图1的有效应力路径可见,在加载-升温试验中,在偏应力值达到 2 MPa前,应力路径与三轴压缩不排水应力路径基本相同,图2中孔压也基本与常温21 °C的试验孔压相同。而当做常载升温的试验时,偏应力值基本保持在2 MPa不变,而有效球应力迅速减小,有效应力路径呈水平直线向左延伸,最终应力状态达到了临界状态。由图1所示,升温不仅改变了有效应力路径,同时,临界状态应力比也有所提高,但在最终的温度92 °C时,试验点的有效应力状态点达到了临界状态线,已经导致了试样的破坏。由此可见,单纯地升温过程同样应视为一种加载过程。由试验结果可见,升温过程导致了排水条件下的体积收缩趋势,使黏土颗粒间孔隙减小,但由于不排水边界条件的限制,使得正孔压持续增大,如图2中正方形点线所示,在升温过程中孔压迅速增大,有效球应力迅速降低,当应力比达到临界状态应力比时,即使得土体达到破坏条件。

图1 升温对饱和黏土不排水路径的影响Fig.1 Influence of heating on stress paths for saturated clay under undrained condition

图2 升温对饱和正常固结土的孔压影响Fig.2 Influence of heating on pore pressure for saturated normal consolidated clay
姚仰平等[5-6]基于超固结 UH 模型,提出了考虑温度影响的UH模型[7],也即热UH模型。热UH模型能否反映上述不排水条件下加载-升温的应力-应变关系以及临界状态强度变化规律,以及能否基于热 UH模型建立三轴压缩不排水热抗剪强度公式,这些都是本文所要探讨的内容。
2 热UH模型
2.1 当前屈服面与参考屈服面
由于热UH模型是建立在UH模型基础上,因此,在某一温度下当前应力点A所在的屈服面为当前屈服面,可表示为

式中:p、q分别为球应力与剪应力;px0为T0温度下初始状态时屈服面与 p轴右交点的横坐标;MT表示在某一温度 T下的临界状态应力比。cp=(λ-κ)/(1+e0),其中λ为e-lnp坐标系下正常固结线(NCL)的斜率;κ为回弹线的斜率;e0为初始孔隙比;H为硬化参数;ξT是温度影响先期固结压力系数,表示为温度的对数函数:

式中:T为当前温度;T0为初始温度;γ为材料参数,可以通过不同温度下的等向压缩试验确定。
某一温度T下的先期固结压力pxT与T0下的先期固结压力px存在如下关系:

由式(2)、(3)可以看出,随着温度T的增大,其相应的先期固结压力随之减小,这表明了温度升高导致了超固结土一部分超固结度的丧失。参考屈服面可表示为

2.2 超固结参数RT
由于在任一温度下,两屈服面具有相同的MT,因此,屈服面几何形状相似,以当前屈服面与参考屈服面的相似比来表示超固结参数RT,可表示为

将参考屈服面的表达式(4)变形得到:

则将式(6)代入到式(5),得到:

超固结状态下的RT是一个小于1的数,随着加载的进行RT值递增,当RT为1时到达临界状态。
2.3 临界状态强度
在式(1)中,MT为某一温度 T下的临界状态应力比。由Hueckel等的试验结果可知,升温不仅会使正常固结线在e-lnp空间下移,导致孔隙比变小,还对临界状态时强度特性造成影响。对于饱和黏土的试验结果表明,升温会提高临界状态应力比。考虑到ξT是一种由温度所导致的温度超固结参数,则类比由应力所形成的超固结参数R,仿照潜在强度的表达式形式构建了受温度超固结影响的临界状态强度表达式。受温度影响的临界状态应力比可表示为

式中:

式中:M0为初始温度T0下的临界状态应力比。随着温度的升高,临界状态强度值逐渐增大。这主要是由于温度升高导致孔隙水活动性增强,从而增加有效应力,使土体变密实,内摩擦角变大,提高了临界状态强度值。
2.4 热弹性模量与泊松比
基于笔者等提出的热UH模型,在文献[7]中已经仔细分析了Campanella和Mitchell得到的不同温度下饱和伊利黏土在e-lnp坐标系下的等向压缩-回弹试验结果。由试验规律可知,不同温度下回弹线基本保持平行状态,只是随着温度升高,回弹线保持平行状态向下平移,则对应的回弹线斜率κ也应完全相同,即不受温度影响。而由κ所决定的弹性模量E也就不受温度影响,仍与原超固结UH模型中弹性模量所用公式相同,泊松比ν也仍然作为一个常数使用,确定为0.3。
3 考虑温度影响的三轴压缩不排水抗剪强度表达式
基于热UH模型,推导饱和黏土在不排水条件下受温度影响的不排水抗剪强度表达式。其基本思路是根据屈服面方程,由体变为0以及临界状态强度特性条件,将不排水抗剪强度式由土性参数以及初始应力条件表示出来。由于处于不排水条件下,因此体变为 0。总体变可分解为塑性体变与弹性体变之和:

则可利用参考屈服面中塑性体应变与当前屈服面中塑性体应变相同这个特征,通过求取参考屈服面中的塑性体应变得到其表达式。则参考屈服面方程经过变形可得到:

又因为:

联立式(11)~(14)可得到:

由弹性部分:

考虑初始 K0固结状态,则由当前屈服面式(1),以及K0的定义:

式中:σ110、σ220、σ330分别是K0固结时的大、中、小主应力。
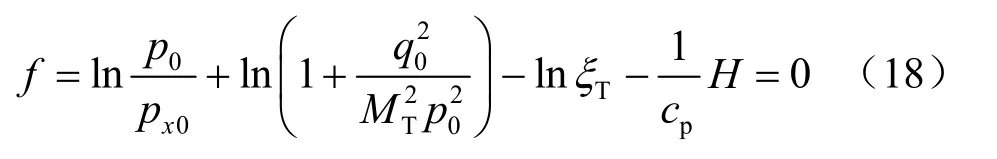

联立式(10)、(15)、(16)、(19)得到:

在不排水条件下,且达到临界状态,则此时超固结应力比参数RT的值为1,且应满足下述条件:

将式(21)、(22)代入到式(20)中,得到:

将式(19)代入到式(23)中,得到:

因为在临界状态,满足:

不排水抗剪强度su在三轴压缩下表示为


式(27)为可考虑超固结度升温条件下的不排水抗剪强度表达式。下面分几种情况进行讨论:
①当温度为常温T0时,则ξT=1,若土体处于等向正常固结状态,则RT0=1,K0=1,则表达式为

式(28)即退化为Wood所提出的抗剪强度表达式;
②当温度保持为常温T0时,若考虑超固结度的影响,则式(27)可表示为

式(29)即为只考虑超固结度影响的不排水抗剪强度表达式,其中,M0和R0分别为T0温度下的临界状态应力比以及初始超固结应力比参数;
③当土体为正常固结状态,温度由常温T0升高到T时,则式(27)可写为
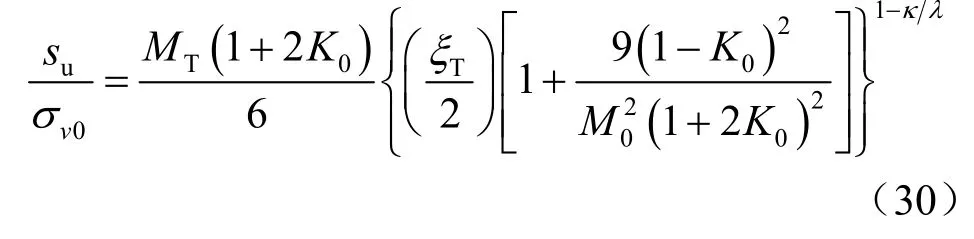
式(30)即为只考虑温度升高时正常固结土的不排水抗剪强度表达式。
采用Kuntiwattanakul等[8]关于一种黏土的不排水强度试验结果来模拟所提出的抗剪强度公式。由于文献并未提供相关参数,因此,可采取表1所示的参数值来进行计算,利用所式(27)来对公式进行功能上的模拟,初始等向固结球应力为196 kPa。

表1 黏土材料参数Table 1 Material parameters for clay
如图 3所示,分别采用OCR为1、2.2、4、8的黏土在不同设定温度下进行不排水剪切测试,由图可见,随着温度的升高,抗剪强度呈增大趋势变化,随超固结度的提高,抗剪强度也随之提高。利用式(3)、(13)分别计算出ζT和MT,由初始K0条件代入到式(32)中,得到在不同超固结度下升温过程的强度值。图4为采用抗剪强度式(27)模拟的结果,不仅能够考虑超固结度提高抗剪强度提高的规律,而且也随着温度的提高抗剪强度也相应的提高。可见,所提公式可简单、合理地反映温度以及超固结度对于不排水抗剪强度的影响规律。

图3 温度与不同超固结度黏土抗剪强度的关系试验结果Fig.3 Relationships between temperature and shear strength under undrained condition for clay with various OCRs

图4 温度与不同超固结度黏土抗剪强度的关系模拟Fig.4 Simulation of relationships between temperature and shear strength under undrained condition for clay with various OCRs
4 热UH模型不排水剪切分析及模拟
由于在某一固定温度下超固结土体的变形以及强度特性与超固结UH模型所描述的相类似,因此,本节着重讨论在固定应力状态下,温度的升高对于土体的变形以及强度等方面的影响。
4.1 三轴不排水常载升温过程
如图5所示,在某一温度T0下,考虑正常固结黏土在不排水条件下由A点加载到B点,然后保持外加载荷不变,保持不排水条件,则此时升高温度,由T0持续升温,当升高到T1时,则达到C点。在初期不排水加载过程中,应力路径如AB所示,在升温过程中,由于保持外载不变,因此,剪应力保持不变,而在点划线所示的等q平面内,应力路径如图BC所示,升温过程造成正塑性体应变产生,由于不排水条件的限制,因此,产生正孔压,造成有效应力减小,球应力从 pB减小到 pC,此时,应力状态达到临界状态。对于超固结黏土,则在升温过程中造成超固结度的损失,使超固结土逐步还原为正常固结土,同时,临界状态强度从 M0增大为MT。对于某些对温度敏感的黏土类型,比如ξT会随温度增大而迅速减小,则使超固结性很快退化为正常固结土,使应力状态很快达到临界状态。

图5 三轴不排水常温加载-常载升温过程Fig.5 Process of loading with constant temperatureheating with constant loading under triaxial compression undrained condition
与上述在p-q空间中的加载过程相对应,如图6所示,在e-lnp空间中,当温度在某一温度T0下时,当进行不排水三轴压缩时,应力状态从A点达到B点,此时,正常固结线与临界状态线相互平行。达到B点后,从T0开始升温到达T1,则对于正常固结土而言,若继续升温,则应力状态点从B点平移到达C点,在升温过程中,临界状态线向下平行移动到T1点。若此时状态点与临界状态线相交,则表明土体达到临界状态。

图6 常温加载然后升温常载过程的不排水应力路径Fig.6 Stress path in e-lnp space under undrained condition with constant loading-heating process
4.2 三轴不排水模拟
在常温剪切至某一预定值后,外载不变、升温不排水的过程已有了相关的测试结果,采用Hueckel等[9-10]分别在1987、1990年对正常固结黏土的测试结果,以及Hueckel等[11]和Del Olmo等[12]关于超固结黏土的测试结果,试验条件如引言中所述。对试验过程进行模拟,由于原文献并未提供所需的模型参数数值,因此,为便于热UH模型对Boom黏土在不排水常载升温下的应力-应变关系进行功能上的演示,根据黏土的常用取值范围,选取模型参数如表2所示。

表2 Boom黏土材料参数Table 2 Material parameters for Boom clay
利用所提的热UH模型模拟上述不排水升温加载过程,强度结果如图7(a)中的M21与M92所示,显示了升温过程中临界状态强度提高的过程。由应力路径的模拟结果可见,黑实线与正常固结土常温不排水模拟基本一致。对于正常固结土的常温加载常载升温的模拟如图中虚线所示,对于升温过程中球应力沿水平直线减小的规律能够明显反映出来,并最终达到临界状态,使土体产生了破坏作用。图7(b)的纵坐标表示孔压用初始平均应力来归一化,正常固结土在常温下不排水剪切与试验结果基本吻合,常温加载升温常载模拟的轴向应变偏小,但反映出升温后孔压增大的规律。对于超固结土也存在相似的规律,图8(a)所示的是超固结度为3的Boom黏土的不排水试验路径,在偏应力达到0.9 MPa时开始升温过程,图8(b)为相对应的模拟结果,由此可见,对于超固结土的常载升温应力-应变关系也能得到合理的模拟。

图7 模拟结果Fig.7 Simulation results

图8 超固结土试验与模拟结果Fig.8 Test and simulation results for overconsolidated clay
5 不排水条件下热应力-应变特性分析
为了便于分析不同应力比条件下升温过程对于变形和强度特性的影响以及超固结度对升温不排水过程的作用,选取一组参数,对应力比条件、超固结度、先期固结压力等因素对于升温不排水的变形与强度特性做一比较。选取参数如表3所示。

表3 黏土材料参数Table 3 Material parameters for clay
初始等向平均应力为200 kPa,设置常温条件为20 °C。在20 °C条件下的临界状态强度记为M20,温度在90 °C条件下的临界状态强度记为M90。则如图9所示,在20 °C条件下做不排水三轴剪切至应力比分别为0.2、0.4、0.6、0.8时保持外载不变。此时再做载荷不变,升温到90 °C的升温控制。
模拟结果如图 9(a)所示,从下到上依次为升温过程的有效应力路径,升温过程中,球应力迅速减小,而剪应力保持不变,同时临界状态强度从 M20增大到 M90。当应力比设定值较大时,如 0.6、0.8时都使应力比达到了临界状态,形成了破坏现象。图9(b)为相应的偏应力与偏应变关系。从图9(c)可看出,在应力比较小时若开始升温,则其剪切模量较常温时呈增大规律,偏应变较常温时呈减小规律。应力比越大或者剪应力越大,则升温对其剪应变有加速增大趋势。

图9 不同应力比下升温不排水应力-应变特性模拟Fig.9 Simulation of heating under undrained condition with various stress ratios
当设定应力比为 0.7时,则在应力比小于 0.7时保持20 °C条件下的不排水三轴剪切过程,直到应力比达到0.7。当达到0.7时,保持外载不变,并实施升温过程。由图10(a)可见,在温度依次升高到40 °C、60 °C、80 °C、90 °C 时,临界状态强度逐渐增大,有效应力持续沿水平方向向左减小,在温度达到90 °C时,达到了临界状态,构成了热破坏现象。图10(b)所示为相应的偏应力随剪应变的发展过程,图10(c)为相应的应力比偏应变关系。

图10 应力比为0.7下升温不排水应力-应变特性模拟Fig.10 Simulation of heating under undrained condition with constant stress ratio 0.7
为便于分析超固结度对于升温不排水的影响规律,只将参数γ由0.6设定为0.15,其他参数不变。当设定不同先期固结压力时,分别制取先期固结压力为200、400、800、1 600 kPa的式样,然后回弹至平均应力为200 kPa。仍然设定控制应力比为0.7,在达到0.7后保持外载不变并做升温的模拟。其应力路径如图11(a)所示,当超固结度较小时,则有效应力减小迅速,应力比也偏小,随着超固结度的增大,则有效应力减小的幅度很小,同时,剪应变也在升温过程中变化很小。其偏应力、应力比与偏应变关系分别如图11(b)、(c)所示。

图11 不同先期固结压力下升温不排水应力-应变特性模拟Fig.11 Simulation of heating under undrained condition with various preconsolidation pressures
在相同先期固结压力,不同的当前平均应力下做不排水剪切的模拟结果如图12所示,图12(a)为初始平均应力分别为1 600、800、400、200 kPa下的常温剪切到应力比为0.7,然后外载不变升温的应力路径模拟结果。控制应力比仍设定为 0.7,由图可以看出,影响应力路径的仍然是超固结度,而先期固结压力对升温不排水的变形以及强度特性影响很小,图 12(b)为对应的偏应力与偏应变关系,图12(c)也显示了同图 11(c)相同的受超固结度影响的规律。

图12 相同先期固结压力下升温不排水应力-应变特性模拟Fig.12 Simulation of heating under undrained condition with constant preconsolidation pressure
6 结 论
(1)根据已有的试验结果可知,在不排水条件下,升温会造成土体的孔压持续增大,使有效球应力迅速减小,并最终造成热破坏现象,因此,不排水条件下的升温过程应视为一种加载过程。
(2)根据所提的热UH模型,由不排水条件推导得到了能够反映温度影响的不排水抗剪强度表达式,并通过相关试验结果的规律验证了公式的合理性。
(3)由所提的热UH模型成功模拟了热破坏过程中土体的应力-应变关系以及临界状态强度变化规律。
[1]BALDI G, HUECKEL T, PELLEGRINI R. Thermal volume change of the mineral-water system in low-porosity clay soils[J]. Canadian Geotechnical Journal, 1988, 25(4): 807-825.
[2]BOURROS C M. The effect of temperature change on consolidation and shear strength of saturated cohesive soils[D]. USA: University of Washington, 1973.
[3]JEFFERSON I, ROGERS C D F, SMALLEY I J.Discussion: ‘Temperature effects on undrained shear characteristics of clay’ by Kuntiwattanakul et al[J].Soils and Foundations, 1996, 36(3): 141-143.
[4]HUECKEL T, PEANO A, PELLEGRINI R. A constitutive law for thermo-plastic behaviour of rocks: An analogy with clays[J]. Surveys in Geophysics, 1993,15(5): 643-671.
[5]姚仰平, 李自强, 侯伟, 等. 基于改进伏斯列夫线的超固结土本构模型[J].水利学报, 2008, 39(11): 1244-1250.YAO Yang-ping, LI Zi-qiang, HOU Wei, et al.Constitutive model of over-consolidated clay based on improved Hvorslev envelope[J]. Journal of Hydraulic Engineering, 2008, 39(11): 1244-1250.
[6]姚仰平, 冯兴, 黄祥, 等. UH模型在有限元分析中的应用[J].岩土力学, 2010, 31(1): 237-245.YAO Yang-ping, FENG Xing, HUANG Xiang, et al.Application of UH model to finite element analysis[J].Rock and Soil Mechanics, 2010, 31(1): 237-245.
[7]姚仰平, 杨一帆, 牛雷. 考虑温度影响的 UH模型[J].中国科学(E辑), 2011, 41(2): 158-169.YAO Yang-ping, YANG Yi-fan, NIU Lei. UH model considering temperature effect[J]. Science in China(Series E), 2011, 41(2): 158-169.
[8]PISIT K, IKUO T, KANTA O, et al. Temperature effects on undrained shear characteristics of clay[J]. Soils and Foundations, 1995, 35(1): 147-162.
[9]HUECKEL T, BORSETTO M, PEANO A. Modelling of coupled thermo-elasto-plastic-hydraulic response of clays subjected to nuclear waste heat[M]. Chichester: John Wiley, 1987: 213–235.
[10]HUECKEL T, BALDI G. Thermoplasticity of saturated clays: Experimental constitutive study[J]. Journal of Geotechnical Engineering, 1990, 116(12): 1778-1796.
[11]HUECKEL T. Water-mineral interaction in hydromechanics of clays exposed to environmental loads:A mixture-theory approach[J]. Canadian Geotechnical Journal, 1992, 29(6): 1071-1086.
[12]DEL OLMO C, FIORAVANTE V, GERA F, et al.Thermomechanical properties of deep argillaceous formations[J]. Engineering Geology, 1996, 41(1-4): 87-102.
