基于等效加速度的岩质边坡爆破动力稳定性＊

陈 明，卢文波，周创兵，舒大强，许红涛

（1.武汉大学水资源与水电工程科学国家重点实验室，湖北 武汉 430072；2.武汉大学水工岩石力学教育部重点实验室，湖北 武汉 430072；3.中国东方电气集团公司，四川 成都 610036）

岩质高边坡在开挖爆破作用下的稳定性分析是一个十分复杂的问题，也是水利水电、采矿等工程领域中需要深入研究的问题。目前，岩质高边坡爆破动力稳定性问题的研究主要是基于极限平衡法、动力有限元法、离散元方法等。其中极限平衡法由于原理简单，能够直观判断边坡安全与否并给出定量性指标参数——安全系数，因此，一直以来被广泛应用于岩质边坡的动力稳定性分析。采用极限平衡法分析边坡的爆破动力稳定性时，对爆破振动加速度的处理主要采用拟静力法。

许多研究者对岩质高边坡爆破动力稳定问题进行了研究。H.T.Ling等［1］采用用拟静力法评价了岩体边坡在地震激励及爆破振动作用下的稳定性；A.Kesimal等［2］基于拟静力法采用刚体极限平衡方法分析了爆破振动作用下某石灰岩采石场边坡的动力稳定性；杨桂桐［3］以Sarma法为基础，将爆破振动动力荷载等效转化为静力，利用极限平衡分析法研究了高边坡爆破开挖动力稳定问题；张永哲［4］、甄胜利［5］、李维光等［6］也采用拟静力法，将爆破振动加速度以某一折减系数转化为静力，然后用极限平衡理论计算边坡稳定性。有研究发现，如果简单地将爆破振动荷载等效成静力参与到极限平衡分析中，则不足以反映边坡在爆破振动荷载作用下的动力响应，必须综合考虑爆破振动波传播过程中的幅值衰减、频谱特性和相位角变化等因素［7］。为此，一些学者［7－10］综合各种因素，采取多种方法评价边坡在爆破振动荷载作用下的动力稳定性，如许红涛等［10］基于刚体极限平衡分析方法中的Sarma方法，提出了一种计算岩质高边坡爆破开挖情况下动力稳定性安全系数的时程分析方法。

采用拟静力法研究边坡爆破动力稳定性时，对爆破振动峰值加速度的处理一般是根据质点振动速度与加速度的关系，由振动速度转换得到，或者是根据实际加速度监测得到，然后以某一折减系数将其转化为拟静力，再利用极限平衡理论分析边坡的稳定性。上述方法对爆破振动加速度的处理均忽略了振动加速度、振动频率与边坡体振动位移、应力状态的内在联系，C.H.Dowding［11］分析了不同频率的爆破振动下二维层状边坡的变化，结果表明在质点峰值速度或加速度恒定时，增加的主振频率极大地减少了剪切位移，这表明振动频率对边坡体的稳定性有重大影响；陈明等［12］基于边坡中的应力、振动速度、振动加速度以及频率之间的关系，提出爆破振动作用下边坡极限平衡分析的等效加速度计算方法。

本文中基于刚体极限平衡分析的Sarma法及等效加速度计算方法，以某一时间步长进行爆破过程中潜在滑坡体稳定性分析，求得任意时刻相应爆破动力作用下的稳定性安全系数。为正确评价爆破振动对边坡稳定的影响、优化边坡爆破开挖设计提供理论依据。

1 基于Sarma法的边坡稳定性分析

刚体极限平衡法中的Sarma法中考虑了滑体本身的强度，可以处理具有复杂结构面的边坡，是公认的计算具有节理切割的岩体边坡稳定性分析的有效方法［13］。

以滑坡体中的任意条块i为例，在某一任意时刻，假定作用在条块上的水平向和竖直向爆破振动惯性力分别为Fx，i、Fy，i，引入的临界水平体积力KcWi，使得滑坡体处于极限平衡状态，如图1所示，由静力平衡方程：∑X＝0，∑Y＝0得

图1 第i条块受力示意图Fig.1 Diagram of the forces acting on slice i

式中：Ti、Ni分别为作用在第i条块底面的剪力、法向力；Kc为临界水平地震加速度系数；Wi为第i条块重量；Xi、Xi＋1分别为作用于第i侧面和第i＋1侧面的剪力；Ei、Ei＋1分别为作用于第i侧面和第i＋1侧面的法向力；Fi为作用于坡顶的外荷载；δi、δi＋1分别为第i侧面、第i＋1侧面与竖直方向的夹角；αi为第i条块滑面与水平方向夹角。

由莫尔－库仑准则得

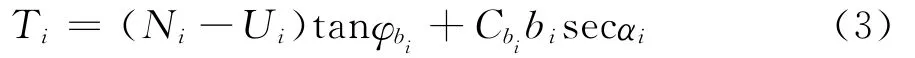
式中：Ui为作用于第i条块底面上的水压力；φBi、Cbi为滑面上强度参数；bi为第i条块底面宽度。

同时假定两侧面力E、X亦处于极限平衡状态，则可得

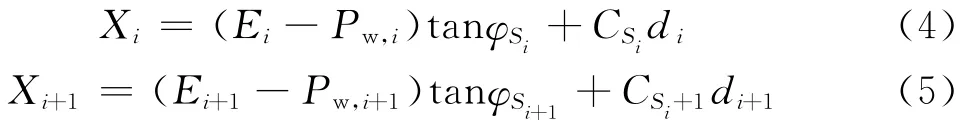
式中：Pw，i、Pw，i＋1分别为第i、i＋1侧面水压力；φSi、CSi为条块侧面强度参数；di、di＋1分别为第i、i＋1条块侧面的长度。

由式（1）～（5）联立求解，可得到临界水平地震加速度系数Kc的计算式。当Kc＝0时，对应的安全系数即为该时刻爆破振动惯性力作用下的边坡动力稳定安全系数f［10］。

按某一时间步长对整个爆破振动过程进行计算，可以得到边坡稳定安全系数随时间的变化规律。在整个爆破振动持续时间范围内，选取最小的安全系数作为整个边坡的动力稳定安全系数。

2 基于等效加速度的爆破振动惯性力

爆破振动惯性荷载通过加速度确定。在边坡开挖爆破振动监测中，往往只监测爆破振动速度。因此，在边坡岩体的爆破动力稳定性分析中需建立质点峰值振动速度和加速度之间的关系。

目前对爆破振动速度衰减规律的研究通常采用回归分析方法。根据工程条件和实践经验，选取合适的拟合公式，然后通过实测资料进行回归分析，可得到爆区质点峰值振速衰减规律。本文中，考虑到爆破振动沿距离、边坡高程和深度方向的衰减，对质点峰值振动速度衰减规律采用下式拟合

式中：V为质点峰值振动速度；K为场地参数；Q为单响药量；R为爆心距；H为潜在滑体中心与爆源高差；D为潜在滑体中心离地表的深度；α、β、γ为衰减参数。

忽略整个潜在滑体区域内的频率衰减，并假定该区域的振动由某一主频控制，则爆破振动速度在水平与竖直2个方向上的分量均具有如下形式

此时，加速度可由速度求导得到

式中：η为爆破振动随时间的衰减指数；ω、φ0分别为爆破振动波主频和初相位。

实际工程中，如果能直接获得边坡上各点的真实爆破振动速度或加速度时程曲线，来替换式（7）或式（8），则计算结果更切合实际。

爆破振动加速度由爆源逐渐传递到边坡上各点，因此边坡各点的加速度变化与这些点至爆源的距离密切相关，可用下式表示

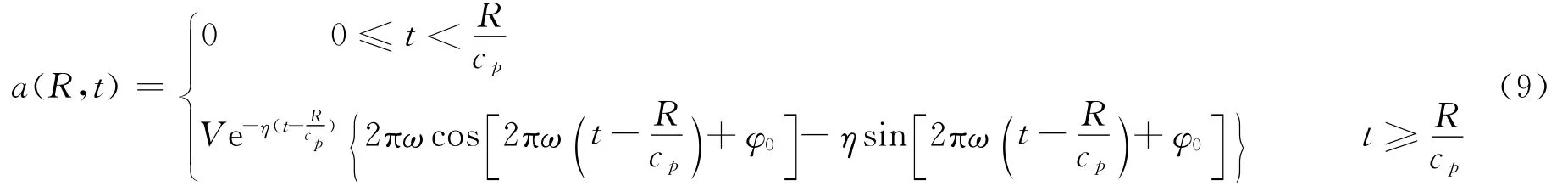
式中：a（R，t）为t时刻在爆心距为R处的振动加速度，cp为岩体中纵波传播速度。

在基于刚体极限平衡法的边坡爆破动力稳定性分析中，通常采用折减系数法分析爆破振动荷载，即按下式将爆破振动惯性力等效成静力荷载

式中：β0为爆破动力折减系数；K0为地震系数，K0＝a／g，a为爆破振动加速度，g为重力加速度；W 为边坡中潜在滑体计算条块的重量。有研究建议粗略计算时直接取β0＝0.1～0.3［14］，李海波等［15］利用反应谱法确定β0为0.008～0.152。

式（10）中忽略了爆破振动加速度与边坡应力状态之间的内在联系，可能导致异常的结果。本文中基于等效加速度计算方法［12］，在分析边坡的爆破动力稳定性时，对式（9）中t时刻在爆心距为R处的振动加速度a（R，t）求其等效加速度

式中：aeq（R，t）为a（R，t）的等效加速度，θ为等效加速度的频率影响系数，取1.05。

于是，得到第i个条块某方向上的惯性力为

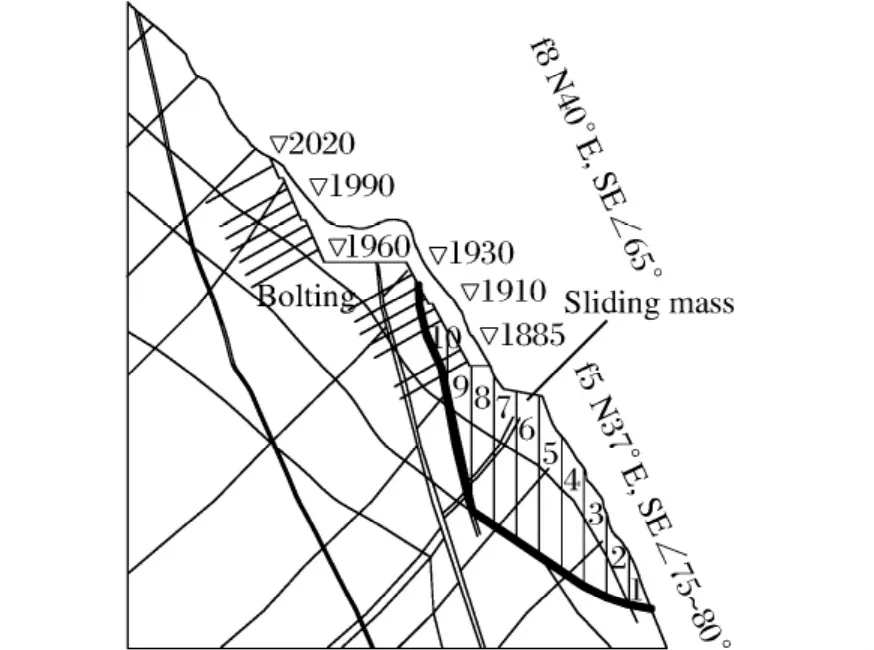
图2 左岸缆机平台1－1断面滑动模式Fig.2 Asliding mode of section 1－1of cable－machine platform at the left bank

式中：Fi（R，t）为爆心距为R的条块i在t时刻的惯性力，aeq，i（R，t）为条块i的等效加速度。根据边坡条块中心各方向的加速度，利用式（12）可求得条块水平、竖直向的爆破振动惯性力Fx，i和Fy，i随时间的变化规律。求得爆破振动惯性力项后，即可代入式（1）～（5）中，参与整个潜在滑坡体的稳定极限平衡分析，计算出整个爆破地震波作用过程中任一时刻潜在滑动体的稳定安全系数，以最小的安全系数作为边坡的爆破动力稳定安全系数。

3 算例分析

3.1 工程概况

锦屏一级水电站位于四川省盐源县与木里县交界的雅砻江干流，装机容量为3.6GW，水电站工程场地边坡规模大，自然谷坡高陡，地应力水平较高，岩体卸荷强烈，并发育有断层、层间挤压带、深部裂缝，地质条件复杂。

所考察的滑动模式，即：f8断层＋弱卸荷分界线＋剪断Ⅳ1类岩体。共划分10个垂直条块，如图2所示，条间参数及滑面参数见表1，表中C为滑面和条间的内聚力，ψ为滑面和条间的内摩擦角。在采用Sarma法计算时，条块界面参数取值根据所穿过的岩体强度参数决定，如条块界面穿越不同质量的岩体，根据穿越长度取加权平均值得到。

荷载工况主要考虑在1 885m高程以下进行台阶爆破时对潜在滑体稳定性的影响。根据该工程爆破振动实测资料，取场地参数K＝78，取衰减参数α＝1.3，不考虑观测点与爆源高差的影响及振动沿边坡往里深度方向的衰减规律，即式（6）中的β和γ均取为0（此时安全系数较实际值小）。考虑爆破振动随时间的衰减，取式（8）、（9）中的衰减指数η＝10.0。

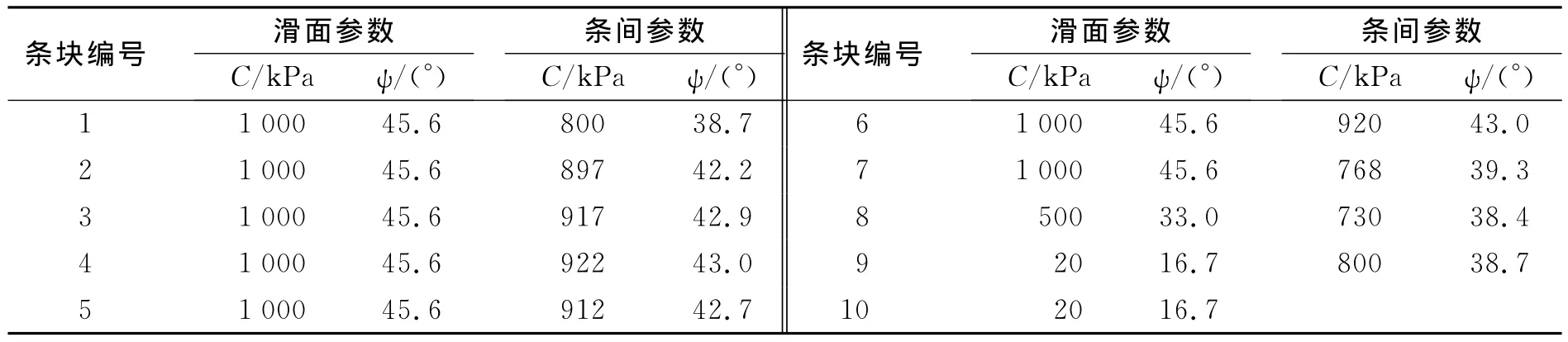
表1 潜在滑体条块计算参数Table1 Parameters of slices of potential sliding slope

3.2 动力稳定安全系数时程曲线

边坡开挖爆破单响药量为100kg左右。利用边坡爆破振动的等效加速度及Sarma法，分别计算了爆破振动主频为10、30和60Hz等3种工况下的边坡动力稳定安全系数时程曲线，如图3所示。图3中还给出了边坡的静力稳定安全系数为2.248，以及边坡在Ⅶ度地震0.125g荷载作用下的稳定性安全系数为2.122。结果表明，边坡动力稳定安全系数在静力稳定安全系数值左右振荡，这是由于爆破地震波的相位变化导致不同时刻各条块上振动惯性力的方向不同所造成的；这种振荡随频率的增大而加快衰减，并且由于振动的衰减，随着时间的推移，最终趋向稳定于静力稳定安全系数。

为比较基于等效加速度及常规折减系数拟静力法得到的边坡稳定系数间的差别，同等条件下，按式（10）计算爆破振动惯性力，取β0＝0.2，得到边坡在爆破振动主频为10、30和60Hz时基于折减系数的爆破动力稳定安全系数f，并对2种方法计算得到的爆破动力对边坡稳定影响的成果进行比较，见表2。表中选取动力稳定安全系数时程曲线上的最小值作为边坡的动力稳定安全系数。

图3 基于等效加速度的边坡爆破动力稳定安全系数时程曲线Fig.3 Time－history curves of dynamic safety factors of high slope based on equivalent acceleration

表2 安全系数比较Table2 Comparison of safety factors from two methods

图3及表2的结果表明，基于等效加速度的边坡爆破动力稳定安全系数，爆破振动频率越高，对边坡稳定性的影响越小，与文献［16］中的爆破动力对边坡稳定影响的有限元研究成果一致。计算工况下，基于等效加速度的边坡爆破动力稳定系数与静力稳定分析结果相比，爆破振动对边坡安全系数的影响为2%～4%。而基于折减系数的爆破动力稳定安全系数，爆破振动频率越高，对边坡稳定的影响越大，最高时可能导致边坡稳定系数降低46.6%，与工程实践经验不一致。可见，采用等效加速度拟静力法，因考虑了爆破振动荷载与边坡体中实际应力状态的关系，能更合理评价边坡的爆破动力稳定性。

实际上，由于算例分析的边坡静态稳定系数较高，在爆破惯性力一定时，体现出爆破振动惯性力对边坡稳定影响较小，而若边坡稳定系数较低时，爆破振动对边坡稳定的影响将增大。对于实例分析的边坡，若初始的静态稳定系数为1.10，则爆破振动将使边坡稳定系数降低4%～8%。

4 结 论

（1）分析爆破振动对边坡稳定性的影响，必须考虑爆破振动的频谱特性、振动加速度与边坡应力状态的关系。可利用爆破振动等效加速度计算方法，基于刚体极限平衡分析法中的Sarma法，根据边坡体中爆破振动荷载随时间的变化规律，得到岩质边坡爆破动力扰动下稳定性系数随时间的变化规律。

（2）基于等效加速度的拟静力法，可合理评价爆破振动对边坡稳定性的影响，而常规的折减系数法可能放大爆破振动对边坡稳定性的危害影响。

（3）工程实例分析结果表明，对稳定性较好的边坡，在爆破振动荷载作用下，稳定性安全系数一般降低2%～4%，爆破振动主频率越高，则边坡的动力稳定性系数越大。

［1］Ling H I，Cheng A H D.Rock sliding induced by seismic force［J］.International Journal of Rock Mechanics and Mining Sciences，1997，34（6）：1021－1029.

［2］Kesimal A，Ercikdi B，Cihangir F.Environmental impacts of blast－induced acceleration on slope instability at a limestone quarry［J］.Environmental Geology，2008，54（2）：381－389.

［3］杨桂桐.爆破振动效应及边坡动态分析［J］.爆破，1989，6（4）：9－14.YANG Gui－tong.Blast shock effect and slope dynamic state analysis［J］.Blasting，1989，6（4）：9－14.

［4］张永哲.岩质高边坡开挖爆破动力稳定分析［J］.工程爆破，1996，2（4）：31－38.ZHANG Yong－zhe.Dynamic stability analysis on blasting and excavation of rock high slope［J］.Engineering Blasting，1996，2（4）：31－38.

［5］甄胜利.岩质高边坡开挖爆破动力稳定分析研究［C］∥工程爆破文集：第五辑.武汉：中国地质大学出版社，1993：110－113.

［6］李维光，张继春.爆破振动作用下顺层岩质边坡稳定性分析［J］.爆炸与冲击，2007，27（5）：426－430.LI Wei－guang，ZHANG Ji－chun.Study on rock mass bedding slope stability under blast seism［J］.Explosion and Shock Waves，2007，27（5）：426－430.

［7］卢文波，赖世骧，朱传云.岩石高边坡爆破震动动力稳定分析［J］.矿冶工程，1996，16（1）：3－7.LU Wen－bo，LAI Shi－xiang，ZHU Chuan－yun.Analysis of the dynamic stability of rock slopes under blasting vibration conditions［J］.Mining and Metallurgical Engineering，1996，16（1）：3－7.

［8］阎坤，张云.岩质高边坡爆破动力稳定分析方法研究［J］.水力发电，1996（8）：27－29.YAN Kun，ZHANG Yun.Study on dynamic stability analysis method of the high side－slope rock blasting［J］.Water Power，1996（8）：27－29.

［9］蒋名政.爆破振动对高陡边坡稳定性影响的试验研究［D］.昆明：昆明理工大学，2002.

［10］许红涛，卢文波，周创兵，等.基于时程分析的岩质高边坡开挖爆破动力稳定性计算方法［J］.岩石力学与工程学报，2006，25（11）：2213－2219.XU Hong－tao，LU Wen－bo，ZHOU Chuang－bing，et al.Time history analysis method for evaluating dynamic stability of high rock slope under excavation blasting［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25（11）：2213－2219.

［11］Dowding C H，Gilbert C.Dynamic stability of rock slopes and high frequency traveling waves［J］.Journal of Geotechnical Engineering，1988，114（10）：1069－1088.

［12］陈明，卢文波，舒大强，等.爆破振动作用下边坡极限平衡分析的等效加速度计算方法［J］.岩石力学与工程学报，2009，28（4）：784－790.CHEN Ming，LU Wen－bo，SHU Da－qiang.Calculation method of equivalent acceleration for limit equilibrium analysis of slope under blasting vibration［J］.Chinese Journal of Rock Mechanics and Engineering，2009，28（4）：784－790.

［13］陈祖煜，汪小刚，杨健，等.岩质边坡稳定性分析——原理·方法·程序［M］.北京：中国水利水电出版社，2005.

［14］丁玲方.爆破动荷载折算系数的确定［C］∥第三届全国岩石动力学学术论文选集.武汉：武汉冶金科技大学出版社，1992.

［15］李海波，吴绵拔.反应谱分析在确定动载折减系数中的应用［J］.工程爆破，1998，4（2）：16－19.LI Hai－bo，WU Mian－ba.Application of spectrum theory in determining the discounted coefficient of dynamic loading［J］.Engineering Blasting，1998，4（2）：16－19.

［16］李启发.爆破地震波对岩质边坡稳定性的影响［J］.爆破，1995，12（3）：1－4.LI Qi－fa.The effect of detonating on the stability of a rocky slope［J］.Blasting，1995，12（3）：1－4.