圆柱装药在偏心定向起爆时水中近场压力特性＊

安丰江，吴 成，王宁飞

（1.北京理工大学宇航学院，北京 100081；2.北京理工大学机电学院，北京 100081）

水中兵器战斗部装药在偏心定向起爆时，会显著改变水下爆炸流场特性并表现出局部压力偏高的定向性，即正对起爆点方向的一定范围内具有较大的压力值［1］，这有利于提高战斗部的毁伤能力。但偏心定向起爆造成的近场峰值压力的增益情况目前尚不清楚，相关研究成果也很少。

关于水下爆炸压力场特性的研究，目前多借助于数值模拟方法，这是因为水中爆炸近场的冲击波峰值压力达到吉帕量级，对如此高的压力进行测量还存在很大困难［2］，炸药装药与水介质初始界面处以及近场水介质冲击波压力特性的实验数据基本上属于空白［3］。

本文中针对圆柱形UHL－5装药在侧向9点偏心定向起爆方式下的水下爆炸近场处压力场特性，从水下爆炸近场实验和数值模拟2个方面进行研究。使用双Π型锰铜压阻传感器测量冲击波峰值压力，并与几何中心点起爆方式下的峰值压力进行对比，初步得到近场处峰值压力的增益特性。

1 水下爆炸近场实验

水下爆炸近场峰值压力测量实验在半径42.5m、深度13.5m的爆炸水池中进行，将5kg圆柱形UHL－5装药放置于水下5m处。装药几何尺寸为：∅150mm×173mm。采用侧向9点起爆和几何中心点起爆2种起爆方式。其中侧向9点起爆方式是指将圆柱形装药的底面分成8个相位，选择其中相邻的3个相位起爆，每个相位上设置3个起爆点，如图1所示。

由于水下爆炸压力场的高压特性，特别是在水中爆炸的近场，冲击波压力达到吉帕量级，在压力测量上存在很大困难，需要特殊的高量程传感器［4］。采用量程可达50GPa的双Π型锰铜压阻传感器［5］，实验测试系统如图2所示。锰铜压阻测试系统主要包括脉冲恒流源、示波器、锰铜压阻传感器、炸药装药，以及测试电缆。其中，恒流源的工作电压为400～450V，触发后，可在700μs内稳定输出9A的电流。示波器的采样时间为0.2ns。锰铜压阻传感器的阻抗为0.05～0.20Ω，敏感部分长1～2mm，宽0.2～0.6mm。

每次实验在装药中心点所在的水平面设有3个测点，如图3所示，测点与装药中心距离相同而方位角不同，目的是为了比较相同距离、不同方位处的水中冲击波超压峰值的差异。也是受限于锰铜压阻测试系统本身，近场测试中，在吉帕量级的压力作用下，传感器都是一次性的，当传感器采集到信号后，敏感材料随即失效，使得整个测试系统的大电流导入水中，从而干扰其他传感器的正常工作。如果将各个传感器都布置在距药柱相同距离处，则可以排除这种干扰。考虑到起爆装置占据一定空间并对主装药水下爆炸近场流场的影响，所以传感器主要放置在正方向0～90°范围内的几个方位角。

图1 侧向9点与几何中心点起爆方式Fig.1 Schematic of nine detonation points on the explosive charge

图2 水下爆炸近场压力峰值测量系统示意图Fig.2 Schematic of peak pressure measuring system

示波器采集到测点的典型压力波形如图4所示。应当注意，在采用恒流源的情况下，实际上是以电压值的相对变化来表示传感器阻值的相对变化，即ΔR／R0＝ΔU／U0，根据锰铜传感器标定函数得到冲击波超压峰值

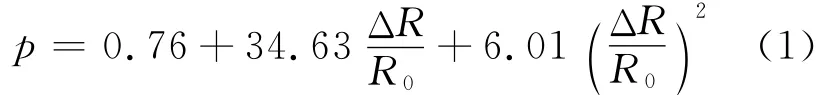
图4中AC段是恒流源为传感器的供电阶段，在B点后恒流源供电趋于稳定，AB间的电压值为U0；CD段为冲击波脉冲阶跃，D点的电压信号对应冲击波峰值压力，CD间的电压改变为ΔU。由于锰铜传感器感受到冲击波阶跃信号后随即损坏，因此只能记录冲击波峰值压力数值，不能得到冲击波衰减历程。

图3 测点布置Fig.3 Layout of gauge points

从锰铜压阻测试系统的特点可以看出，恒流源的工作时间决定了应当在距离装药较近的范围内设置测点，但一次实验中测点数量较少，因此需要进行多次实验并结合数值模拟技术以得到较为全面的水下爆炸压力场特性。

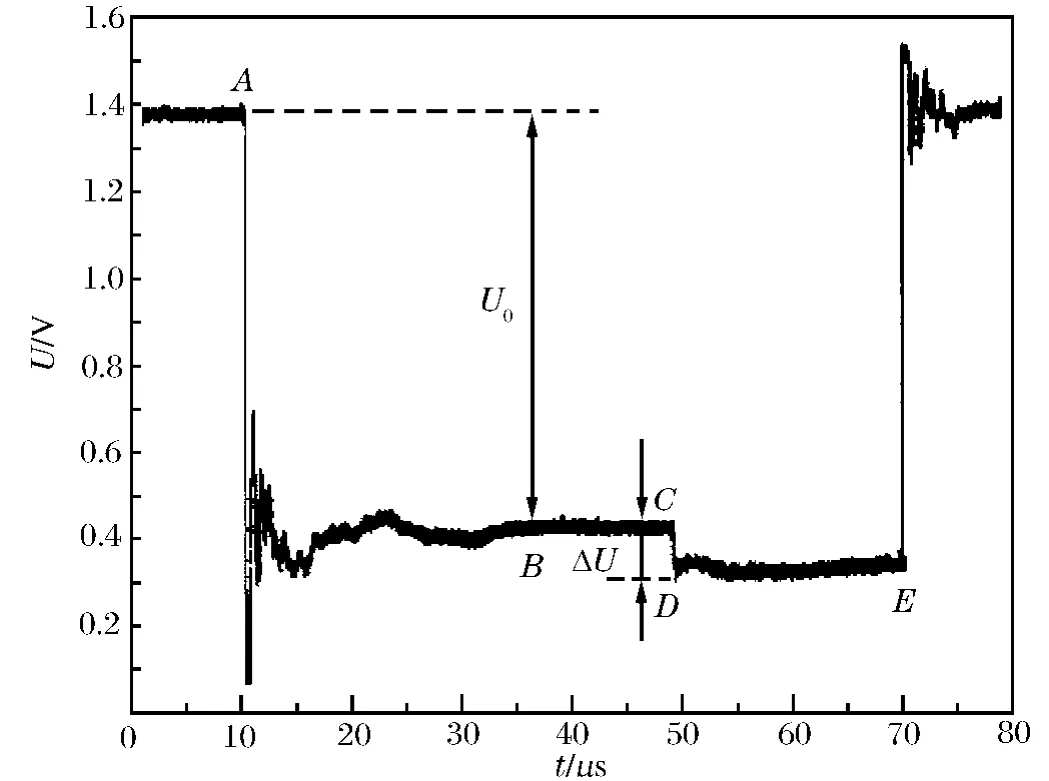
图4 水下爆炸近场实验典型测量波形Fig.4 Typical experimental waveform in the near field of underwater explosion

2 水下爆炸近场数值模拟

使用ANSYS／LS－DYNA软件的ALE算法建立有限元模型，对水下爆炸近场进行数值模拟，得到任意方位角及爆距处的冲击波峰值压力，以解决锰铜传感器实验系统测点位置受限和测点数量偏少的问题。

对于质量为5kg的UHL－5装药，与水下爆炸实验相对应，计算2种起爆工况，即：侧向9点起爆和几何中心点起爆。鉴于起爆工况具有对称性，计算中可采用1／4对称模型，计算水域为15倍装药直径。周围水域采用球形而非传统的圆柱形以减少计算量，如图5所示。

为求解水下爆炸的近场压力场特性，需要精确模拟炸药的爆轰过程，这就要求网格的划分与爆轰反应的进程相当。在近场区域，冲击波在水中是以指数形式衰减的。这些因素确立了对于近场问题求解的网格划分原则，根据炸药的爆轰速度和反应速率，近场网格的划分应该在mm量级。

图5 有限元计算模型Fig.5 The finite element model

在有限元模型中，主要涉及水和炸药2种介质。对于水介质，使用Mie－Grüneisen状态方程

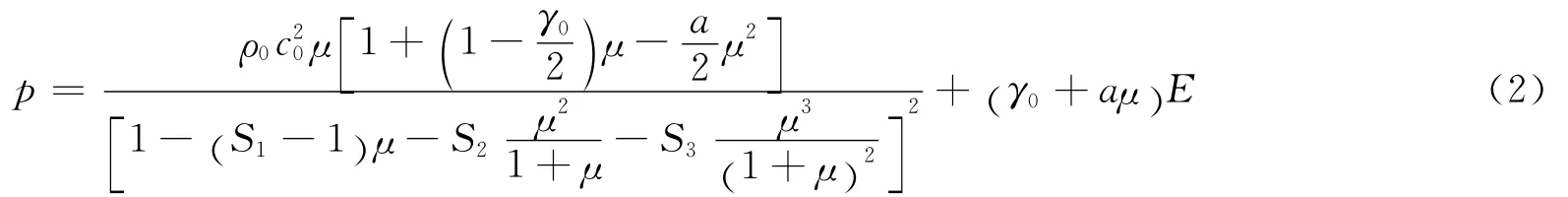
式中：p为压力；E为单位体积的比内能，其初始值为E0，具有压力量纲；ρ0为介质初始密度；c0为介质中初始声速；μ为介质压缩度；S1、S2、S3是常数，通常根据水介质的冲击实验数据确定；γ0为Grüneisen初系数，a为Grüneisen系数修正项。H.M.Steinberg等［6－7］的结果被较多使用，相关参数值如表1所示。

表1 水介质状态方程参数Table1 Mie－Grüneisen equation of state parameters for water

对于炸药的爆轰产物采用JWL状态方程

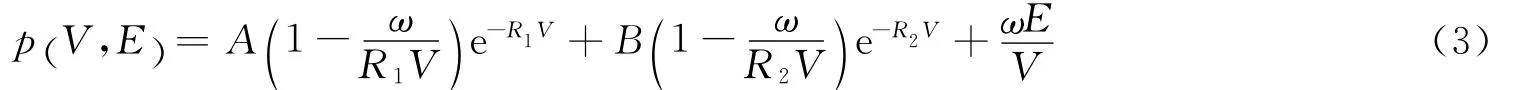
式中：V为爆轰产物的相对比容；A、B、R1、R2和ω为JWL状态方程的5个待定参数。

炸药状态方程是影响数值模拟结果的重要因素。通过理论计算初步拟合得到UHL－5装药的JWL状态方程参数，然后对照水下爆炸近场实验结果，调整状态方程参数，最终确定出JWL状态方程参数，如表2所示，其中ρ为UHL－5炸药密度，D为爆轰速度，pCJ为爆轰压力。

表2 UHL－5炸药JWL状态方程参数Table2 JWL equation of state parameters for UHL－5explosives

3 结果与分析

采用锰铜传感器分别测量5kg的UHL－5装药在侧向9点起爆和几何中心点起爆时水下爆炸近场峰值压力，实验结果综合于表3、表4中，表中同时给出了相应测点处的数值模拟结果。

表3 侧向9点起爆冲击波峰值压力实验数据Table3 The experimental results of shock wave peak pressure for nine－point directed detonation

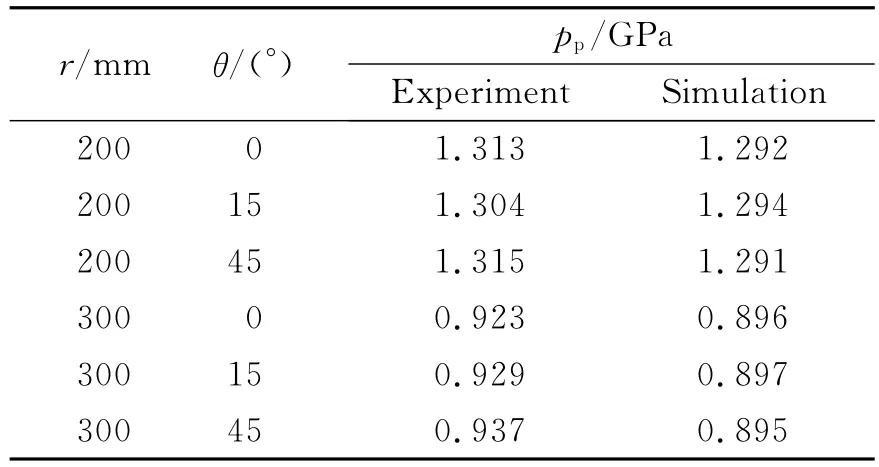
表4 中心点起爆冲击波峰值压力实验数据Table4 The experimental results of shock wave peak pressure for central detonation

根据表3、表4得到2种起爆方式冲击波峰值压力变化图，如图6所示。可以看出，相同工况下，数值模拟结果与实验结果基本吻合，且数值模拟和实验得到的峰值压力随方位角以及随距离变化的规律趋势一致，说明表2中JWL状态方程参数的选取是合理的。

图6 不同方位角冲击波峰值压力Fig.6 The peak pressure varied with angle

图6表明，在距离装药表面200～300mm范围处，采用侧向9点起爆方式时正方向的峰值压力明显高于几何中心点起爆时的峰值压力。其中，在200mm距离处，θ＝0°方向的冲击波峰值压力最大，且随方位角θ的增大，峰值压力从最大的1.958GPa逐渐降低到1.638GPa。中心点起爆时峰值压力为1.311GPa。可见，在θ＝0°的定向条件下峰值压力要比侧向θ＝90°时高出20%，比中心点起爆方式高出49%。在300mm距离处，在θ＝0°～30°范围内，定向条件下各个方向上的峰值压力差别较小，其中θ＝0°时峰值压力为1.317GPa，θ＝30°时峰值压力为1.255GPa，中心点起爆时峰值压力为0.930GPa。此时，θ＝0°时的定向条件下峰值压力要比θ＝30°时高出5%，比中心点起爆方式高出42%。上述结果表明，侧向9点偏心定向起爆能显著改变水下爆炸近场压力场特性。

图7 5kg圆柱形UHL－5装药侧向9点起爆不同爆距处的压力增益Fig.7 The peak pressure gain versus distance at given angles for directed detonation of 5kg cylindrical UHL－5charge

通过实验可以测得定向条件下水下爆炸近场处的峰值压力。距离装药表面更远处以及在起爆点后方90°～180°范围内的峰值压力需要通过数值模拟得到。以中心起爆为基准，将侧向9点起爆条件下某一方位角的峰值压力与中心点起爆时相应方位角峰值压力作对比，定义峰值压力增益Gp＝ （pd－pc）／pc，其中pd为侧向9点起爆时的峰值压力，pc为中心点起爆时的峰值压力，增益为负值时表示峰值压力低于中心起爆时相应位置处的峰值压力。

图7给出了5kg圆柱形UHL－5装药在侧向9点起爆时不同方位角处峰值压力增益随距离变化的数值模拟结果。可以看出，在350mm范围内，0°方向具有较高的增益，而在180°方向增益小于0；350～750mm 范围内，0°、45°、90°方向峰值压力值差别较小，但明显高于135°、180°方向和中心点起爆方式的增益；在750～1000mm范围内，各方向峰值压力值趋于一致。在350、500和750mm等3个距离处不同方位角的增益计算结果如图8所示。在0°～135°范围内，350、500mm距离处具有明显增益，尤其是在0°～90°范围内，在350mm处的增益达到30%，而500mm处的增益只有10%。750mm距离处各方位角增益均不超过4%，说明峰值压力与中心起爆方式趋于一致。由图7～8可知，5kg圆柱形UHL－5装药侧向9点偏心起爆时，在距离750mm、方位角90°范围内，具有明显的峰值压力定向性。

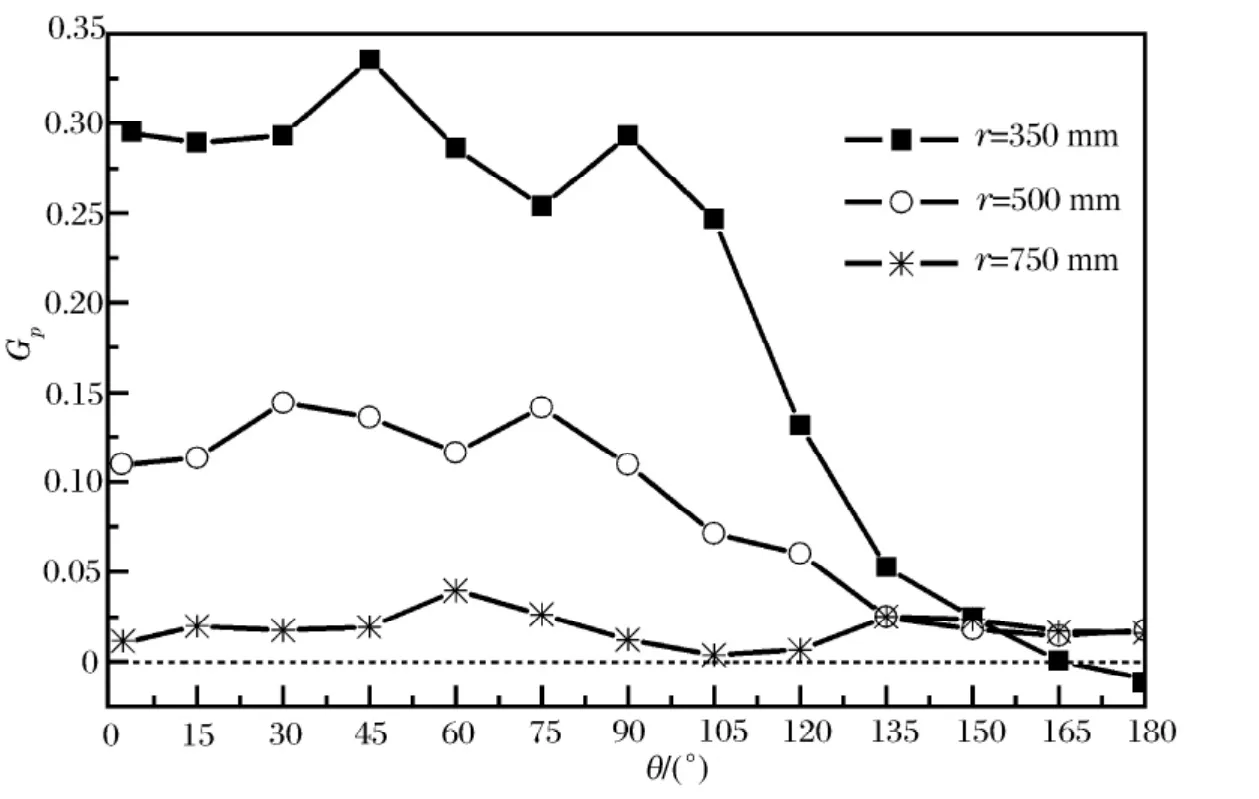
图8 5kg圆柱形UHL－5装药侧向9点起爆不同方位角的压力增益Fig.8 The peak pressure gain versus angle at given distances for directed detonation of 2kg cylindrical UHL－5charge

4 结 论

（1）侧向9点起爆方式的正方向的峰值压力明显高于几何中心点起爆时的峰值压力。在距离装药表面200～300mm范围处，定向条件下0°方向峰值压力比中心点起爆方式高出42%以上。

（2）侧向9点和几何中心点2种起爆方式时的冲击波峰值压力数值模拟结果与实验结果基本吻合。

（3）5kg圆柱形UHL－5装药侧向9点偏心起爆时，在距离750mm、方位角90°范围内，具有明显的峰值压力定向性。其中，在350mm处，增益为约30%；550mm处，增益为约10%；750mm以远距离处各方位角峰值压力与中心起爆方式趋于一致，定向增益可忽略。

［1］Sternberg H M.Underwater detonation of pentolite cylinders［J］.Physics of Fluids，1987，30（3）：761－769.

［2］Cole R H.Underwater Explosion［M］.New Jersey：Princeton University Press，1948：147－209.

［3］WU Cheng，ZHANG Xiang－rong，HUANG Feng－lei.Investigation on the determination of initial shock pressure at near interface field of TNT charge and water for underwater explosion［J］.Journal of Beijing Institute of Technology，2007，16（2）：127－130.

［4］Lee J S，Hokamoto K，Raghukandan K，et al.Development of an underwater dynamic compaction technique for making Al－based composites［C］∥Proceedings of the Conference of the American Physical Society Topical Group on Shock Compression of Condensed Matter.2004（706）：1106－1109.

［5］HUANG Zheng－ping.Explosion and shock measuring technique：Piezoresistive measurement technique［M］.Beijing：National Defense Industry Press，2006：141－170.

［6］Sternberg H M，Hurwitz H.Calculated spherical shock waves produced by condensed explosives in air and water［C］∥Proceedings of the 6th International Detonation Symposium.Coronads，CA，Washington，DC Office of the Chief of Naval Operations，1976：528－539.

［7］Shin Y S，Lee M，Lam K Y，et al.Modeling mitigation effects of watershield on shock waves［J］.Shock and Vibration，1998，5（4）：225－234.