一种改进的基于加权属性的SLOF离群点挖掘算法

赵向兵

（1.太原科技大学计算机科学与技术学院，山西太原 030024；2.山西大同大学数学与计算机科学学院，山西大同 037009）

一种改进的基于加权属性的SLOF离群点挖掘算法

赵向兵1，2

（1.太原科技大学计算机科学与技术学院，山西太原 030024；2.山西大同大学数学与计算机科学学院，山西大同 037009）

SLOF算法采用了空间对象的空间属性和空间关系确定空间邻域，并结合非空间属性的权值来计算对象在其邻域内的离群度，但在计算属性权值时，仍然由邻域专家决定，存在人为因素。文中采用计算每个对象的每个非空间属性的去一划分信息熵增量，并通过这个值来反映各个属性对对象离群的贡献程度，给出一种改进的SLOF算法。实验结果表明，算法具有计算效率高和对用户依赖性小的优点。

高维数据；信息熵；息熵增量；属性权值；偏离因子

离群点检测是数据挖掘的重要分支之一，其目的是在大量的、复杂的数据集合中消除噪音数据或发现有意义的知识。Hawkins对离群点的定义抓住了概念的精髓：“一个离群点是一个观察点，它偏离其它观察点如此之大以至引起怀疑是由不同机制生成的”［1］。典型的应用领域包括在电子商务的犯罪行为探测、网络入侵检测分析。

离群点查找的算法很多，大体上可分为：基于分布的、基于深度的、基于距离的、基于密度的和基于聚类的［2］。近年，Shekhar，Lu和Zhang学者最先提出二分算法［3］，该算法将空间属性与非空间属性区分开，并用对象与其邻域的非空间属性的比值或差值，来表示对象与其邻域的偏差，简称为SLZ算法。SLZ算法没有能够解决空间数据的异质性问题，因而，检测的结果主要是全局离群点。Cbawla和Sun学者同时考虑了空间数据的异质性和自相关性，入波动参数β，且用β和对象与其邻域的欧拉距离的乘积表示空间局部离群度SLOM［4］。但由于对称分布状况决定β，若其在波动幅度较小或空间邻居较少的情况下，很难准确的表现波动情况，因而出现漏检和误检现象。为此，薛安荣等人提出了一种SLOF算法［5］，该算法用计算邻域距离的方法解决空间自相关性问题，用计算空间局部离群系数的方法来解决空间异质性问题，用对象的邻域距离与邻域中对象的平均邻域距离之比表示对象的空间局部离群程度。但此算法在属性权值的确定上，仍然由邻域专家决定，存在人为因素。

本文针对SLOF算法中属性权值确定方面存在的问题，给出了一种SLOF改进型算法，该算法采用计算每个对象的每个非空间属性的去一划分信息熵增量，来确定属性权值，从而消除人为因素，并使算法的用户依赖度进一步减少。

1 基本概念和定义

1.1 信息熵

信息熵是信息论中信息和随机变量的不确定性的一种度量［6］。设X是一个随机变量，其取值集合为S（X），p（x）表示X的概率函数，则X的信息熵定义为：

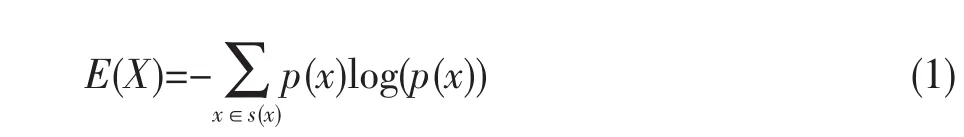
说明随机变量的不确定性越大，信息熵就越大；信息熵值越小，不确定性越小。

1.2 去一划分信息熵增量

设D是对象集合，D的一个子集是S，并且｜S｜＞1，设q是S中的一个对象。则S被对象Q划分为S-｛q｝和｛q｝两个部分，记为=｛C1，C2｝，得到。则E（S）-E（）为子集S去一划分信息熵增量，记为Δ（q，s），S明确的情况下，在下文中简记为Δ（q）。

可以看出Δ（q）表示S被划分为Cˆ的前后信息熵的变化。从统计角度看，离群点挖掘的关键是检测出在全局中占百分比小的数据对象，因为在子集S中Δ（q）值大的对象正是占百分比小的对象，这些对象更有可能是离群对象。也就是说离群点是指数据集合中一旦离群点被删除，整个数据集的“混乱”或“不确定性”就明显减少的数据点。对于对象集合中的某个对象来说，这个对象的每一个非空间属性对这个对象的离群贡献度的大小，就是看一下这个对象每一个非空间属性值在它所对应的非空间属性值集合中的去一划信息熵增量值的大小，即Δ（q）。所以我们用这个Δ（q）要表示非空间属性的权值。

1.3 相关概念

空间邻居：对象d的空间邻居是指与对象d在指定条件c下，存在空间邻接关系σc的对象。即∀d∈D，∃p∈D｛d｝，使得s（p）σcs（d）为真，则对象P是对象d的空间邻居［5］。

空间邻域：对象d的空间邻域N（d）是指对象d的所有空间邻居的集合，即

∀d∈D，N（d）=｛p｜s（p）σcs（d）=ture，p∈D｛d｝｝

加权距离：在对象集D=｛d1，d2，…，dn｝，对象di，dj∈D，di和dj的M-维非空间属性是f（di）和f（dj），则数据对象di，dj之间的M-维非空间属性加权距离

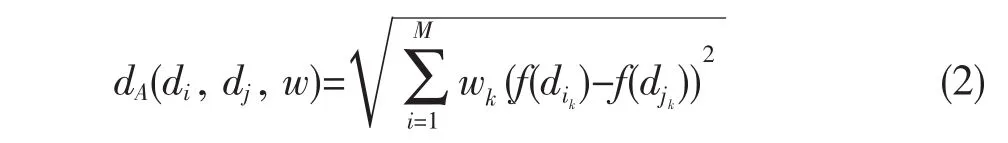
其中：wk是第k维的权值，且0≥wk≥1（这里是对wk做了归一化处理），这个距离表示了两个对象间的偏差。

平均距离：对象d的平均距离是指对象d与其空间邻域中所有对象的加权距离的平均值，即

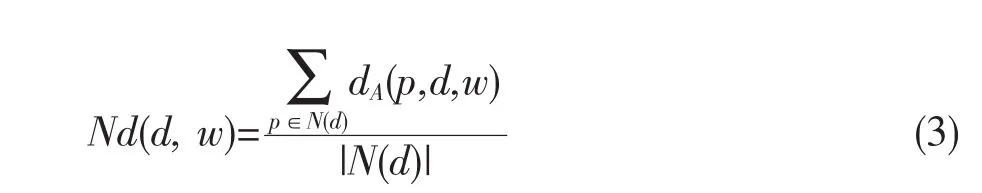
平均距离表示对象与其邻域非空间属性上的偏差，偏差大的离群度就越高。

对象领域密度

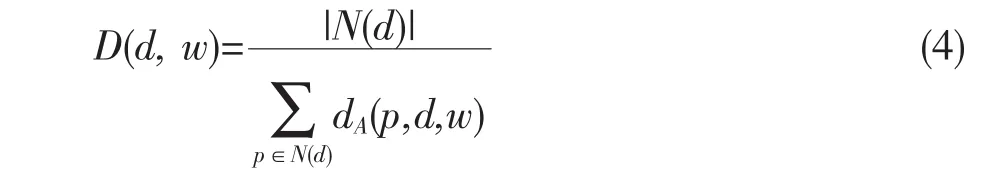
空间局部离群度：空间对象d所有邻居的邻域密度平均值与d的邻域密度的比值得到d的空间邻域偏离因子，即：

KSLOF（d）反映对象d的非空间属性偏离它周边邻居的程度。

2 用去一划分信息熵差量确定非空间属性的权重

在计算对象间非空间属性距离的时候，不同属性对分析目标的贡献程度不同，可用熵权作为非空间属性重要程度的度量。倪巍伟等对属性权值的确定提出了离群属性子集的概念，用局部信息熵描述数据点及其邻域近数据点在属性上投影的分布情况计算离群属性的参考值，组成离群属性子空间，属于此空间的属性赋以大于1的λ值，不属于此空间的属性赋1。这样同样没有对属性的权值做具体的量化，难于区分λ的具体值，且计算时比较复杂，也比较抽象。而SLOF算法对属性权值确定的方法主要是对非空间属性做规则化处理。根据分析需要，给不同贡献度的属性分配不同的权值，贡献度大的权值大，反之则小，权值一般由邻域专家决定。所以这种方法，没有对每个属性的贡献度做具体量化，且很难解释，计算的数值有人为化因素，很难对分析数据做推广。而去一划分信息熵增量很好的解决了以上问题，方法如下：

设对象集合D=｛d1，d2，…，dn｝，由n个对象组成，对象d∈D的空间属性函数s（d），非空间属性函数是f（d），f（d）的维度是m维，m维非空间属性f（d）表示为（f（d1），f（d2），…，f（dm））

按照定性和定量结合的原则得对象非空间属性矩阵：

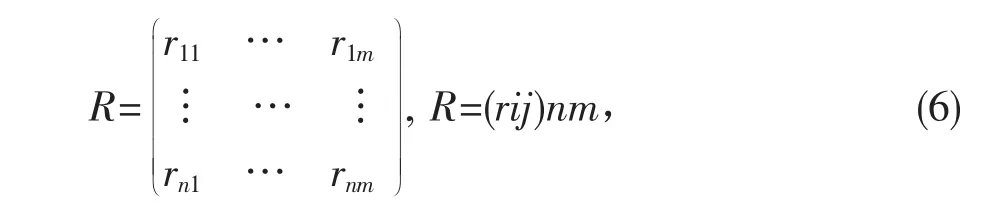
rij表示第i个对象在j-属性上的值。且可以得出：f（dj）=rij（i=1，…，n，j=j）。

设p是m个对象中的第j个对象，所以p对象可以包含矩中m个值且每个值分别对应对象的m个属性值。接着我们可以分别计算这m个属性值在它所对应的属性取值集合中计算去一划分信息熵增量，分别记为Δ（p1），…，Δ（pm）。

对于p，在m维非空间属性中，第j维属性的权值记为wj，且wj=Δ（pj），（j∈m）。

根据去一划信息熵增量的意义可知，对于对象p来说，在每个属性上Δ（q）值越大，对象p的离群度就越大，它所对应的属性的离群度就越大，它的属性权值就越大。进而根据属性权值确定不同属性对分析目标的贡献程度。

3 改进的SLOF离群点检测算法

根据上述分析，采用计算每个对象的每个非空间属性的去一划分信息熵增量，来确定属性权值，从而有效地消除人为因素。其算法描述如下：

输入：对象集D=｛d1，d2，…，dn｝（对象di的空间属性函数s（di），非空间属性函数是f（di），σc表示在指定条件c下的空间邻接关系，m维非空间属性f（di）表示为（f（dj1），f（dj2），…，f（djm）））。

输出：离群度最大的前q个对象

Step1：从集合D中取一对象d，从D中寻找与d存在空间关系σc的所有邻居，并确定对象d的邻域N（d）；

Step2：利用（1）式和（6）式分别计算对象d在非空间属性（f（d1），f（d2），…，f（dm））中各个属性的去一划分信息增量值，分别记为Δ（p1），…，Δ（pm）。从而确定对象d的非空间属性的权值分别为wj，且wj=Δ（pj），（j到m）；

Step3：把wj代入（2）式计算加权距离，并利用（3）式计算对象d与空间邻域中所有对象的加权距离的平均值；

Step4：利用（4）式和（5）式计算对象d的空间局部邻域偏离因子KSNOF；

Step5：计算集合D中其它每个对象的空间邻域偏离因子KSNOF；

Step6：把所对象的空间邻域偏离因子KSNOF按降序排列；

Step7：输出前q个对象，前q个对象就是空间离群点。

分析上述算法，该算法的复杂度为：O（n（klogsn+km+log2n））（k为对象的邻居数），而LOF等算法确定邻域却采用的是全部属性，其复杂度为O（kn2），所以采用此算法离群点检测效率比较高。

4 实验

试验环境：CoreT7500 2.2G CPU，2G内存，操作系统为Windows 2000，数据库为SQL，并采用VC++编写了上述算法。采用某省旅游景点情况统计数据，以200个旅游景点为研究对象，数据中既有空间属性又有非空间属性。对于各个景点，与它相邻的景点可以组成其邻域。选择5个非空间属性：tourists，greenrate，complaints，facilitation，satisfaction。通过20个景点评价对象计算得这五个非空间属性权值p=｛0.18，0.20，0.15，0.19，0.33｝。实验结果表明，这种算法检测出的5个离群点确实是邻域离群点，见表1。

表1 SLOF算法挖掘的5个离群点

为了进一步考察算法的性能，用LCK算法和SLZ算法与该算法进行比较，如图1所示可知，该算法倾向于挖掘邻域离群点，而SLZ算法和LCK算法偏向挖掘全局离群点，采用改进型SLOF算法的检测精度较高，并且准确给出了其它离群数据对象的离群顺序。也证明了改进型SLOF算法结果的得出是充分的考虑了空间数据的相关性和异质性的结果，而SLZ算法和LCK算法都造成了局部离群点的漏选。从时间执行上来看，由于空间属性确定邻域最费时间，这三种算法采用相同的数据和算法，因而确定邻域的执行时间一样，比较总执行时间应在同一数量级上，执行时间分别为SLOF：3.5s，SLZ：3.8s，LCK：4.1s。如果再把数据对象和维数做人工扩充，随着对象和非空间属性维数的增加，SLZ算法和LCK算法执行效率会下降，执行时间也会增加，但改进型SLOF算法却有着很好的伸缩性，执行时间增加幅度小于SLZ算法和LCK算法，因而它有着更好的性能。

图1 检测结果比较

5 结语

该算法充分考虑了空间数据的特点，根据空间关系确定空间邻域，减少了用户指定参数，特别是在非空间属性的处理上，通过计算每个属性去一划分信息熵增量来确定属性权值。进而确定非空间属性的离群程度。此算法是对SLOF算法的改进，且易于解释，去除人为因素的干扰。实验表明，该算法在减少用户依赖度、提高检测精度上具有明显的优势。

［1］Hawkms D.Identification of Outliers［M］.London：Chapman and Hall，1980.

［2］Han Jiawei，Kamber Micheline.Datamining：concepts and techniques［M］.San Francisco：Morgan Kaufmann Publishers，2001.

［3］Gulukota K，Sidney J，Sette A，et a1.Two complementary methods for predicting peptides binding major histocompatibility complex molecules［J］.Journal of Molecular Biology，1997，26：1258-1267.

［4］Brusic V，George R，Margo H，et a1.Prediction of MHC class II-binding peptides using an evolutionary algorithm and artificial neural network［J］.Bioinformatics，1998，14：121-130.

［5］薛安荣，鞠时光，何伟华，等.局部离群点挖掘算法研究［J］.计算机学报.2007，30（8）：1457-1458.

［6］Claude E S.A mathematical theory of communication［J］.Bell System Techical Journal，1948（27）：623-656.

〔编辑 高海〕

SLOF based on Weighted Attribute of the Improved Algorithm for Outliermining

ZHAO Xiang-bing1，2
（1.School of Computer Science and Technology，Taiyuan University of Science＆Technology，Taiyuan Shanxi，030024； 2.School of Mathematics and Computer Science，Shanxi Datong University，Datong Shanxi，037009）

SLOF algorithm uses spatial properties and spatial relationships of spatial objects to determine spatial neighborhood and combined with the weight of non-spatial attributes to calculate the object＇s outlier in its neighborhood.However，the attribute weights are still determined by the neighborhood experts in the calculation，there are human factors.For each object，calculating leave-one division information entropy increment of each non-spatial attribute is introduced in this article when determining the right value of non-spatial attribute.This value can reflect the contribution of stray objects by the various attributes and furthermore an improved SLOF algorithm is given.Experimental results show that the algorithm has high computational efficiency and the advantage of less dependence on the user.

high dimensional data；entropy；entropy increment；attribute weights；deviation factor

O211.7

A

1674-0874（2011）03-0011-03

2011-02-06

赵向兵（1978-），男，山西大同人，在读硕士，助教，研究方向：数据挖掘。