最小失真点位在噪声监测布点中的应用研究

赵利民，李雅丹，苗玉英，王双维

（1.长春市环境监测中心站，长春 130022；2.东北师范大学 物理学院，长春 130024；3.北华大学 物理学院，吉林 132013；4.长春市双阳区环境监察大队，长春 130060）

1 噪声地图的构建

噪声地图（noise mapping）是运用现代计算机技术，将噪声源数据、地理信息、建筑物分布、公路和铁路交通资料等进行综合、分析和计算后生成的反映城市噪声状况的数据地图，它既是评估噪声污染防治措施有效性的重要手段之一，也是环境规划和环境管理过程中的一种有效决策工具。

目前，很多国家都开展了噪声地图方面的相关研究，已形成完整的技术规范和计算方法。英国的伯明翰市是制作噪声地图最早的城市之一，2000年由伯明翰市议会服务部邀请环境声学专家利用专业软件绘制完成该项目，并于2004年再次更新。德国已经绘制噪声地图的城镇有500个，并已经将噪声地图用于环境噪声污染控制工程和工厂的选址。在意大利，许多城市已经建立了噪声地图与GIS相结合的城市噪声管理系统。葡萄牙将城市规划与噪声地图密切联系起来，将噪声纳入城市建设规划，在现有城区管理和新区规划中都有所应用。我国的香港特别行政区构建了基于互联网的噪声地图，公众可在网上浏览三维噪声地图，深入了解和参与城市环境管理。英国在所制定的城市发展环境保护战略中提出，政府要在2010年完成整个伦敦市的噪声地图，建立噪声地图查询网站，并将城市噪声环境和房地产开发密切联系起来。《北京市“十一五”时期环境保护和生态建设规划（草案）》提出，在2010年前建立由城市区域环境、道路交通噪声、铁路噪声、机场噪声自动监测子系统组成的全市声环境自动监测系统，编制城市噪声地图。实践证明，噪声地图的应用有利于噪声控制管理、环境噪声规划和环境评价过程中的公众参与［1-8］。

现有噪声地图的构建过程，是根据环境监测数据应用相应的算法并考虑到建筑物的反射、绿化地声衰减、交通流量等地理信息数据，通过数值计算求出研究区域各点的声评价量。由于GIS系统的快速发展，地理信息数据获取已不再是噪声地图构建的瓶颈，应用计算机也可以方便地进行数值运算。影响噪声地图与实际情况很好吻合的重要原因之一就是监测点位的布设，它包括自动监测点位和用以修正数据的人工监测点位的数量和布设方式。环境噪声监测点位不达到必要的数量并进行合理布设，再充足的地理信息数据、再好的运算模式也得不到与实际情况吻合很好的精确的噪声地图，并非所有情况下都需要高精确度的噪声地图。根据我国的具体国情，本文提出用较少的优化监测点位构建噪声地图的方法。

2 最少支撑点位和最小失真点位的确定

最少支撑点位是指支撑声评价量曲面的必须点位，对于某区域，允许存在一定误差范围内的噪声状况描述，客观上存在着最优监测点位布局，即最少支撑点位，本文采用加法优化的方法确定最少支撑点位［10，11］。

由于经济支撑能力的限制和不同描述程度的需求，要对自动监测点位的个数进行人为设定，而人为设定的监测点位个数常常少于最少支撑点位的个数。用这些人为设定数量的监测点位得到的声评价量曲面相对于最少支撑点位形成的声评价量曲面将会产生失真，在m个最少支撑点位中选n个点位，一定有一组n个点位，用这组监测点位得到的声评价量曲面失真程度最小，将这样一组监测点位命名为最小失真点位。

2.1 最小失真点位个数确定

最小失真点位是在多个失真曲面中确定与原曲面最接近的曲面，即失真程度最小的曲面，是多方案中确定最佳方案的决策问题。由于涉及到布设自动监测点位的经济支撑能力和声环境描述程度等管理因素，自动监测点位个数并不是越多越好。管理因素具有模糊性，会使点位个数的确定随意性太大，不规范。本文以计算机图形学的贝济埃理论为基础，用曲面的贝济埃点作为自动监测点位最小失真点位候选点，使点位数量确定规范化。

“贝济埃模型”用Bernstein多项式逼近曲线或曲面，Bernstein多项式的次数越高，逼近程度也越高。Bernstein多项式的次数决定了贝济埃曲面定义点—“贝济埃点”的个数。把用不同次数Bernstein多项式的贝济埃曲面逼近实际噪声曲面（如区域噪声描述）或实际噪声曲线（如交通线噪声描述）称为对声环境的分级描述，其级次即为贝济埃曲面的Bernstein多项式次数。采用这种描述方式，可以使最小失真点位个数的确定规范化，减少随意性。例如，0级描述需要且仅需要一个监测点位（即平均值点位）；1级描述需要且仅需要3个点位或2个点位；2级描述对于曲面需要且仅需要9个点位，对于曲线需要且仅需要5个点位；……，描述级次根据经济支撑能力和描述目的确定。

2.2 最小失真点位的选择

确定最小失真点位个数n后，可从m个最少支撑点位中选取n个点位作为贝济埃曲面的定义点。选取方案有个，即可以有个同次贝济埃曲面对声环境进行某个级次的描述。本项目将应用灰色关联度分析，比较个同次贝济埃曲面中哪个贝济埃曲面代替最少支撑点位时失真最小。

3 实例研究

3.1 交通噪声最小失真点位选择实例研究

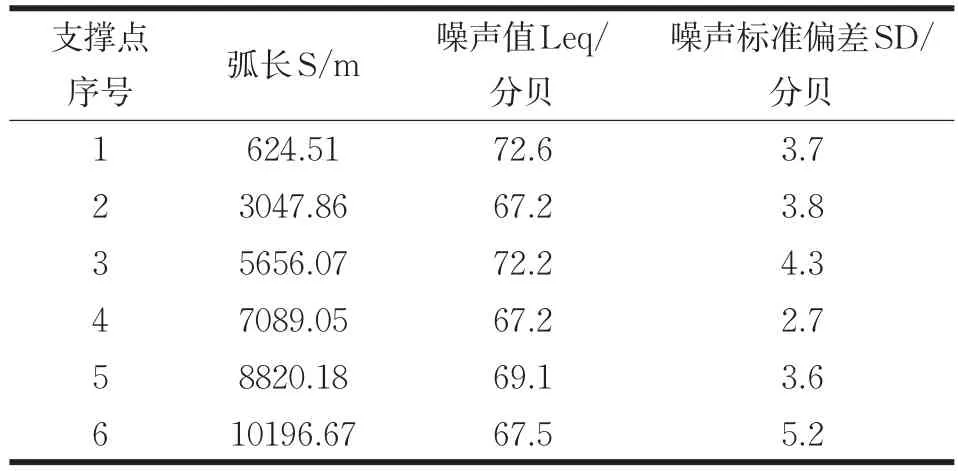
表1 最少支撑点数据Tab.1 Least support point data

将最小失真点位的确定方法应用于交通线噪声监测点位的选择，本文选取吉林省长春市人民大街的交通噪声作为测量样本。人民大街全长13.7km，北起长春火车站，南至高速公路入口，南北方向贯通市区中心，是长春市市区最长的街道；除火车站站前至胜利公园的路段为36m宽外，其余路段宽为54m，整条大街可以近似看成为一条直线型的公路。通过加法优化，确定该交通线共有6个最少支撑点位，其中，弧长以站前广场为起点，最少支撑点数据见表1。

如果6个最少支撑点位选取4个，则依照排列组合原理，可以有15种方式。分别按这15种排列方式取点，运用神经网络进行曲线拟合，可到15个拟合后的序列。将这些序列与6个最少支撑点位拟合的序列进行综合关联度的运算，计算结果如表2。

表2 不同最少支撑点位拟合曲线的灰色关联度Tab.2 Grey relational grade of different fitting curves to minimum support points

由表2看出，组合1、2、5、6关联度最大，所以选择点1，2，5，6为最小失真点。

3.2 区域噪声最小失真点位选择实例研究

通过对吉林省长春市南关区进行区域研究，图1中的区域为解放大路、人民大街、自由大路、吉顺街所包围的区域为小区域，经过加法优化得到最少支撑点位20个。在对该区域进行最小失真点位选择时，采用灰色矩阵关联度理论来分析［9］。

图1 研究小区域的Google earth纬片地图Fig.1 Research on Google earth latitude map in small region

由表3可知，151号点被剔除后，拟合曲面矩阵与20点拟合曲面矩阵的灰色绝对关联度最大，这就说明，剔除点151后，拟合曲面的失真度最小，即151号点位为最小失真点位。同理，再从剔除151点位后的19个点中依次选取18个点，进行多次拟合曲面，进行相同的运算，计算结果如表4，可确定153号点位为最小失真点位。

由表3、表4可知，在剔除151号点位和153号点位后拟合的曲面矩阵与原有20个点位拟合的曲面矩阵的灰色绝对关联度最高，说明剔除这两个点后，所拟合的曲面与原有曲面相比，失真度最小。最小失真点位的个数，可采用计算机图形学的贝济埃理论为基础，用曲面的贝济埃点作为自动监测点位候选点的思路，使点位数量的确定规范化。

表3 剔除不同点位后矩阵绝对灰色关联度Tab.3 Absolute grey relational grade of matrix after eliminating different points

表4 去除151号点位后第二次剔除不同点位后的矩阵绝对灰色关联度Tab.4 Absolute grey relational grade of matrix after second elimination of different points which excluded 151 point

4 结论

经实践验证，本文所采用的优化方法，具有一定的可行性、科学性。既保证了失真度最小，又减少了监测点位的个数，是在空间上对噪声评价量曲面进行对比和优化，为建设适合我国国情的噪声地图生成平台奠定了基础。

［1］刘嘉林，徐谦.北京城市声环境自动监测系统监测点位布设方法初探［J］.中国环境监测，2008，24（2）：17-21.

［2］李红星，王雪平.GIS技术在城市环境噪声中的应用研究［J］.环境科学与管理，2007，32（3）：42-44.

［3］杨光.关于城市环境噪声自动监测工作的思考［J］.环境监测管理与技术，2009，21（4）：9-11.

［4］李红星，赵军.基于GIS的区域环境噪声评价方法研究［J］，遥感技术与应用，2006，21（4）：363-367.

［5］秦勤，张斌，段传波.环境噪声自动监测系统研究进展［J］，中国环境监测，2007，23（6）：38-41.

［6］Noronha Castro Pinto，F A，Moreno Mardones，M D.Noise mapping of densely populated neighborhoods-Example of Copacabana，Rio de Janeiro-Brazil ［J］.Environmental Monitoring and Assessment，2009，155（4）：309-318.

［7］Lee Shi-Won，Seo Chang，Park Young-Min.Utilizing noise mapping for environmental impact assessment in a downtown redevelopment area of Seoul，Korea［J］.Applied Acoustics，2008，69 （8）：704-714.

［8］王寄凡.用声环境地图法改革我国城市声环境质量评价体系初探［J］.噪声与振动控制，2006，（12）：92.

［9］王双维，张莎，赵利民.矩阵灰色绝对关联度及其意义［J］.东北师范大学学报：自然科学版，2009，12（4）：73-78.

［10］赵利民，李雅丹.区域噪声监测点位的“噪声岛”地形布点法应用初探［J］.噪声与振动控制，2011，12：142-146.

［11］赵利民，李雅丹，王双维.城市“噪声岛”模型及其在交通噪声监测点位优化中的应用［J］.声学技术，2009，28（6）：102-105.

［12］马玉芹，贾春明，李文慧，等.基于GIS的长春市NO_X时空分布规律研究［J］.长春理工大学学报：自然科学版，2003，26（2）：92-94.