基于自适应滑模的变质心再入飞行器控制律设计

魏鹏鑫,高长生,荆武兴

(哈尔滨工业大学 航天学院,黑龙江 哈尔滨 150001)

0 引言

变质心控制通过质心偏移实现控制。与通过改变力的方式影响作用在飞行器上控制力矩的方法(如气动舵等)不同,变质心控制是通过调整内部滑块与弹体间相对位置使系统质心发生变化,改变了力臂,从而产生附加稳定力矩控制飞行器姿态运动。虽然变质心机动控制技术有诸多优点,但实现其工程应用仍面临多种问题,飞行控制系统即为其中之一。由于活动质量块在弹体内频繁往复运动,变质心导弹姿态活动质量块动力学模型属于典型的快时变多体系统,大量耦合因素严重影响了系统的动态品质。因此,设计有效的飞行器控制系统是目前变质心飞行器研究的热点。

传统飞行控制律设计主要采用线性控制理论,线性化飞行器模型,针对各种飞行条件对控制系统进行综合,再用增益调度方法获得满意的控制性能[1]。但对具参数不确定性和外部扰动及强非线性的系统,传统设计方法难以确保飞行器获得满意的控制性能。近年来,滑模控制(变结构控制)理论已成功地用于飞行控制系统设计,为具参数不确定性和外部扰动的线性或非线性系统提供了一种强力设计工具[2]。其重要特征是当系统状态到达状态空间的某个流形时,控制器结构发生变化,最主要优点是能通过选择适当的滑动流形而事先确定系统的瞬态性能,系统状态一旦进入并沿滑动流形运动,则对参数摄动和外界干扰具某种不变性。近年来,对滑模控制与自适应控制组合设计飞行控制系统的方法进行了研究,但用于有快时变、强耦合及严重非线性的高超声速变质心飞行器时,实现对姿态的控制仍有很大的挑战性[3]。

针对置有纵向单滑块的侧滑转弯(STT)变质心飞行器,俯仰通道控制采用布置在飞行器纵向的滑块完成,并认为偏航与滚转通道已通过某种控制方式达到稳定。考虑气动力系数等不确定因素,本文对其自适应滑模控制律进行了研究,同时从Lyapunov稳定性角度对系统的不确定性进行自适应估计,以抵消实际系统中不确定项的影响[4-7]。

1 动力学模型建立

1.1 运动学模型

纵向单滑块变质心再入飞行器内部结构如图1所示。系统由本体B和内部滑块1组成。图中：O1为质心;S*为任一时刻系统质心;δy为滑块运动的位置;l1为滑块轴向配置位置。

图1 系统结构Fig.1 Configuration sketch of system

定义坐标系如下。

a)再入坐标系e-xyz：原点e为再入时刻地心与质心O1连线在地球表面的交点;ey轴在地心与质心O1的连线上,指向点O1为正;ex轴在过点e的子午面内垂直于ey轴,指向飞行器运动方向为正;ez轴与ex、ey轴构成右手坐标系。

b)体坐标系O1-xbybzb：原点为质心O1;O1xb轴与再入飞行器的纵轴重合,指向头部为正;O1yb轴在再入飞行器纵向对称平面内垂直于O1xb轴,指向上为正;O1zb轴与O1xb、O1yb轴构成右手坐标系。单位矢量b=[b1b2b3]。

c)速度坐标系O1-xvyvzv：原点为质心O1;O1xv轴与速度方向重合;O1yv轴在再入飞行器纵向对称平面内并与O1xv轴垂直,指向上为正;O1zv轴与O1xv、O1yv轴构成右手坐标系。

d)地心惯性坐标系Oe-xIyIzI(I)：初始时刻与再入坐标系重合,在惯性空间定向。

飞行器的惯性角速度和点O1的惯性速度可分别表示为

式中：(ωTx1,ωTy1,ωTz1),(vx1,vy1,vz1)分别为飞行器的惯性角速度和惯性速度在各弹体轴上的分量。活动质量体在弹体内的位置为

式中：rbx,rby,rbz为r1在各弹体轴上的分量。在O1-xbybzb系中作用于飞行器的气动力Faero可分解为轴向力X、法向力Y和横向力Z,有

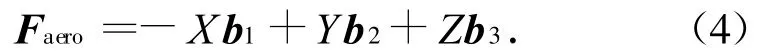
定义气动力对质心O1的矩

式中：T1,T2,T3分别为气动力在各弹体轴上的分量。则,气动力对系统质心S的矩和引力加速度分别为

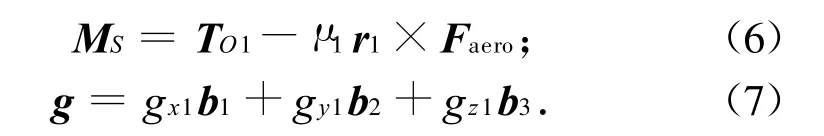
式中：gx1,gy1,gz1分别为引力加速度在弹体轴上的分量;μ1=m1/ms。此处：m1为活动质量体质量：ms为系统质量,且ms=m1+mB。其中：mB为弹体质量。

由牛顿第二定律和动量矩定理,可得在O1-xbybzb系中表示的动力学方程为

式中：JB/O1为弹体对质心O1的惯量张量,且JB/O1=diag[JxJyJz];上标“～”表示反对称阵[8]。此处：Jx,Jy,Jz为惯量张量在弹体轴上的分量。

1.2 动力学方程简化

式(8)、(9)表示的飞行器动力学模型是一复杂的非线性系统,设计控制器时需对两式作必要的简化：忽略重力的影响;不考虑控制量的一阶、二阶项;不考虑滑块偏移引起的惯性主轴偏移项。则可得

式中：α,β分别为飞行器的攻角和侧滑角;Cx1为轴向气动力系数;分别为法向气动力系数和气动力矩系数对攻角的偏导数;为阻尼力矩系数对角速度ωz的偏导数;q为飞行器的动压头;S,L分别为再入飞行器的特征面积和特征长度;v为弹体相对e-xyz系的速度;ωx,ωy,ωz分别为飞行器相对e-xyz系的角速度在O1-xbybzb系中的分量;δy,δyv分别为滑块运动的位置和速度;u1为作用于活动质量体的驱动力[8]。

由式(10)、(11),定义状态向量x1,x2∈R1,控制输入δ∈R1,则有

式中：R为矢量。这样,飞行器姿态运动可表示为

定义式(15)为变质心飞行器的名义模型,基于该模型考虑不确定因素的影响。不确定因素一般分为结构和非结构两类,其中结构不确定性由参数不确定性引起,非结构不确定性包括未知扰动、未建模动态等。则式(15)可进一步表示为

式中：Δf1为由参数不确定性引起的摄动项;ΔB1为姿态角测量误差对系统的影响;ΔB2为由执行机构动态特性引起的输入不确定项;γθ,θ分别为已知平滑函数和不确定参数矢量;d1,d2分别为未建模误差项、未知干扰等非结构不确定项。其中,部分参数不确定项可用光滑函数γθ表示,且存在未知系数θ。γθ,θ的具体表达式为

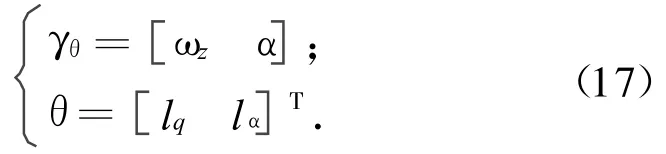
2 控制器设计

将内回路控制问题分为两部分：一是姿态跟踪控制回路,完成对制导指令输入的跟踪,采用滑模控制和自适应控制方法进行设计;二是活动质量体位置伺服控制回路,完成对姿态角控制所需活动质量体位移的跟踪,采用滑模控制方法进行设计。综合两个回路构成完整的俯仰通道飞行控制系统,控制流程如图2所示。

图2 俯仰通道姿态控制原理Fig.2 Attitude control principle for pitch

2.1 姿态自适应滑模控制律

采用滑模控制设计鲁棒控制系统,先需设计一滑模面(切换函数)。通过此滑模面选定控制律,使系统的状态轨迹在此滑模面上具期望的运动特性。为实现系统输出的无静差跟踪,设计滑模面为

式中：e为状态输出跟踪误差,且e=yc-y=yc-x1;c1,c2为正定对角阵。此处：yc为所设计的期望输出。通过选择合适的c1,c2可使输出跟踪误差具有期望的动力学特性。

对x1求时间的二阶导数,得

采用滑模控制的闭环系统运动包括两个阶段：一是滑模到达阶段,系统从任意初始状态向滑模面s=0运动,且在有限时间内到达;另一是滑模运动阶段,状态轨迹沿设计的滑模面s=0运动,且收敛至期望的状态。

设计产生滑模运动的控制律时,为满足自适应滑模设计要求,忽略ΔB1,ΔB2,微分式(18),并代入式(19),有

式中：

为保证趋近过程的运动品质,采用指数趋近律,设计的滑模控制律为

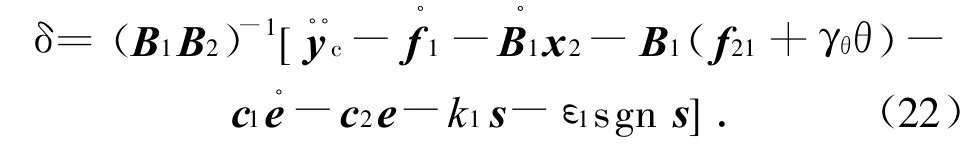
式中：k1＞0;ε1＞0。

对单纯滑模控制要求知道不确定参数矢量的有界性,且当系统面临大的不确定性时,为获得好的跟踪性能需增大控制增益,这常会导致控制颤振的进一步加剧;自适应控制对参数不确定性无界限要求,通过参数自适应补偿可抵消不确定性的影响,降低控制增益,在获得跟踪性能的同时有效解决颤振问题。在式(22)的滑模控制律中考虑对不确定项的补偿,则控制律为

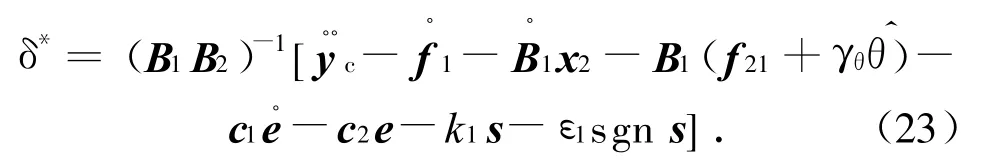
此处：Γθ为正定对角阵。

假设在状态轨迹包含的领域Ω1内满足关系式

令Lyapunov函数

将式(26)代入式(27),并由式(25)可得

若取

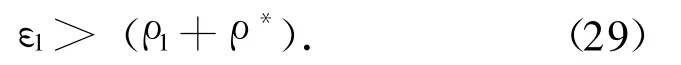
式中：ρ*为一大于零的正数。则有

2.2 滑块伺服控制回路控制律

根据活动质量体控制模型式(12)、(13),定义状态变量x3,x4∈R1,控制输入u∈R1,则有

式中：x3,x4分别为活动质量体偏移量和偏移速度。由此活动质量体控制模型可表示为

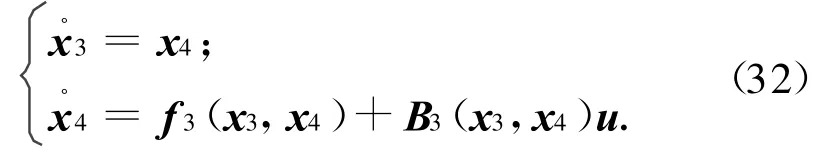
式中：|B3|=;|f3|=((ωx)2+(ωz)2)×δy-l1ωxωy-。

对输出状态x3微分两次,可得输入输出间关系为

设计滑模面为

微分式(34),并将式(33)代入,可得

令

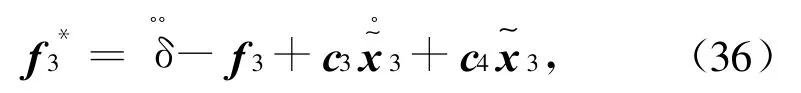
考虑系统存在不确定因素,式(35)可进一步表示成更一般的形式

式中：Δf3,ΔB3分别为模型和输入不确定项。

设计Lyapunov函数

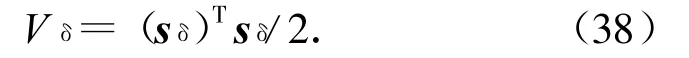
微分式(38)可得

因det B3≠0,设计滑模控制律为

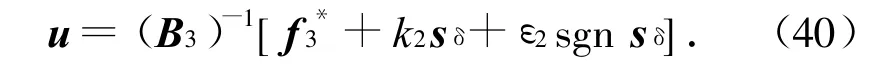
式中：k2＞0,ε2＞0。

假设在状态轨迹包含的领域Ω2内满足关系式

式中：ρ2,ρ3为正数。式(41)的第一个不等式限制了输入矩阵的不确定性应很小,通过适当的估计可确定ρ2,ρ3的值。

将式(40)代入式(39),则有

由式(41)可得

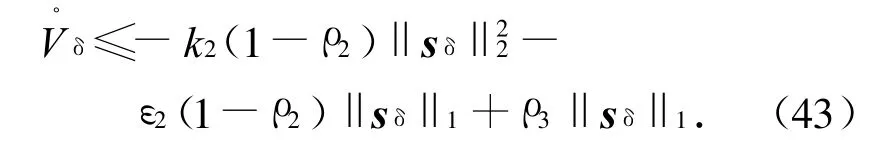
将

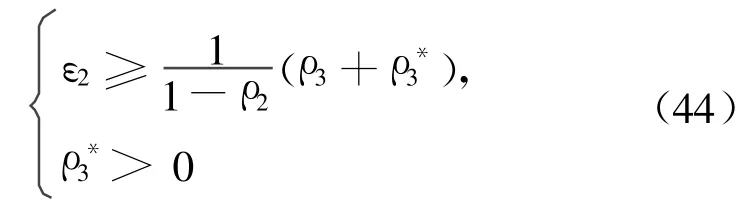
代入式(43),可得

式(45)表明状态轨迹沿着设计的滑模面趋近至零,即x3→δ。

至此,活动质量体伺服回路控制系统设计完成。

为消除不连续函数产生的控制颤振,可将控制式中符号函数sgn换成连续函数sat,即

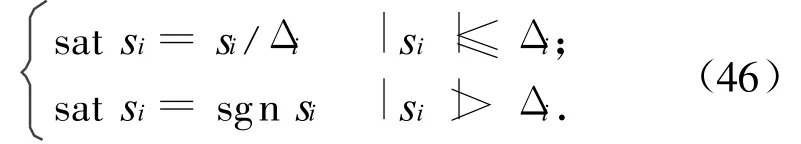
式中：i=1,2;Δ1,Δ2分别为在滑模线s=0,sδ=0附近设置的边界层厚度。

3 仿真

为验证所设计控制律的有效性,将本文滑模控制律式(40)和自适应滑模控制律式(23)、(24)用于式(8)、(9)表示的系统。设置仿真参数为：飞行高度h=10 km,飞行马赫数Ma=8：初始姿态角(γ,α,β,θ,ψv)=(0°,0°,0°,-40°,0°);初始姿态角速度(ωx1,ωy1,ωz1)=(0,0,0)(°)/s;指令姿态角(γc,αc,βc)=(0°,1°,0°);ms=1 000 kg;飞行器特征长度lk=4 m;特征面积SM=0.5 m2;弹体惯量张量

JB/O1=diag[(100 1 000 1 000]kg◦m2;l1=0 m;滑块最大偏移量δymax=±0.2 m。名义模型的滑模控制仿真结果如图3～5所示。其中：相关系数为c1=5.5,c2=0.2,c3=25,c4=0.01,k1=7,k2=40,ε1=0.1,ε2=0.01,Δ1=0.5,Δ2=0.01。

图3 标称模型仿真所得αFig.3 Simulationαfor nominal model

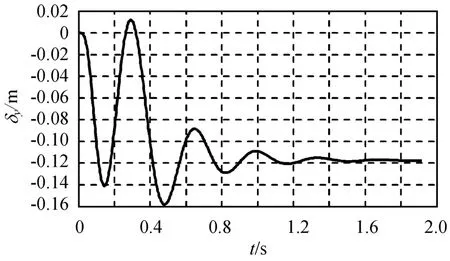
图4 标称模型仿真所得δyFig.4 Simulationδyfor nominal model

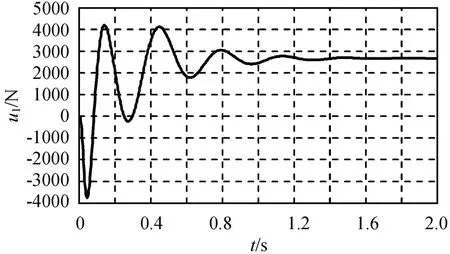
图5 标称模型仿真所得u1Fig.5 Simulation u1for nominal model

由图3～5可知：设计的控制律的控制效果较佳,攻角响应快速,约0.35 s即可达到期望的指令状态,同时超调较好,整个动态响应过程良好;滑块在初始阶段经历较大幅度的振荡,随后平稳过渡,同时发现对指令位移能实现较理想的跟踪;伺服驱动力保持在小于4 k N,且过渡平滑,未出现大幅振荡,保证了跟踪效果。仿真结果表明本文设计控制器能有效消除跟踪误差,同时保证过渡过程的动态品质。

基于标称系统模型,考虑气动参数不确定性影响,设轴向力、法向力相对标称值有10%的偏差,确定参数初始估值较真实值亦有10%的偏差。俯仰通道单纯采用滑模控制时的仿真结果如图6～8所示。

图6 含不确定干扰的滑模控制器仿真所得αFig.6 Simulationαfor sliding modecontroller with uncertain disturbance

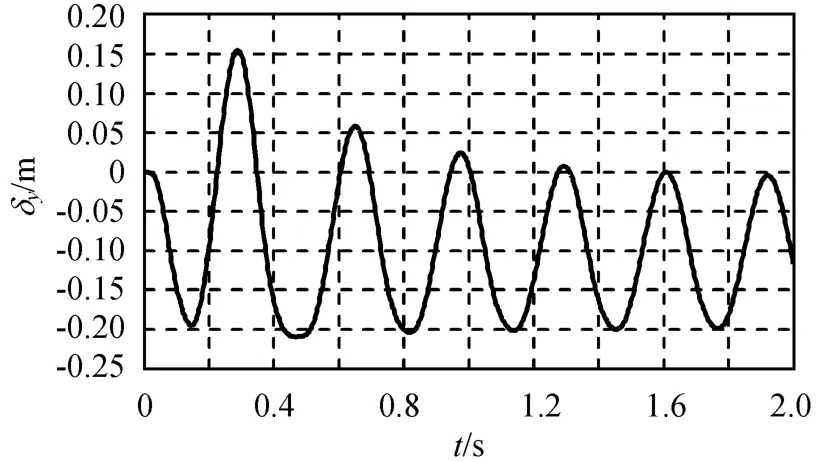
图7 含不确定干扰的滑模控制器仿真所得δyFig.7 Simulationδyfor sliding mode controller with uncertain disturbance

由图6～8可知：单纯依靠滑模控制克服参数不确定性效果很不理想。为消除参数不确定产生的稳态误差,仿真中控制参数c1=15(增大),但由图可发现仍存在颤振,活动质量体经历了大幅度的切换。这将导致执行机构消耗的能量过多,是工程实现中所不允许的。

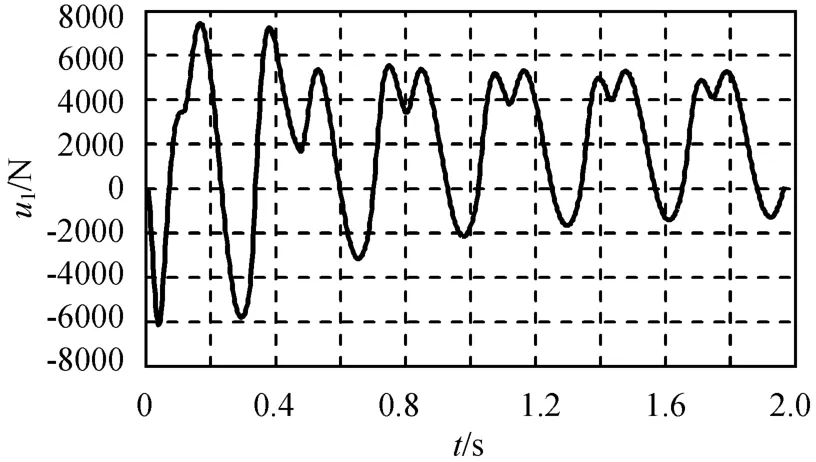
图8 含不确定干扰的滑模控制器仿真所得u1Fig.8 Simulation u1for sliding mode controller with uncertain disturbance

加入对不确定参数自适应估计后的仿真结果如图9～11所示。仿真中c1=5.5(恢复为图6～8水平),控制参数的减小降低了滑块的伺服驱动力。由图9～11可知：虽然存在较大超调,但控制颤振消除,并最终实现对指令的跟踪。

图9 含不确定干扰的自适应滑模控制器仿真所得αFig.9 Simulationαfor adaptive sliding mode controller with uncertain disturbance

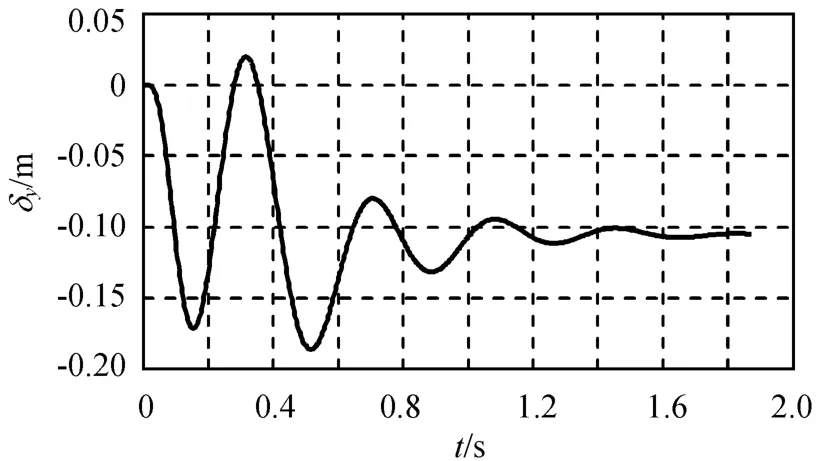
图10 含不确定干扰的自适应滑模控制器仿真所得δyFig.10 Simulationδyfor adaptive sliding mode controller with uncertain disturbance

图11 含不确定干扰的自适应滑模控制器仿真所得u1Fig.11 Simulation u1for adaptive sliding mode controller with uncertain disturbance

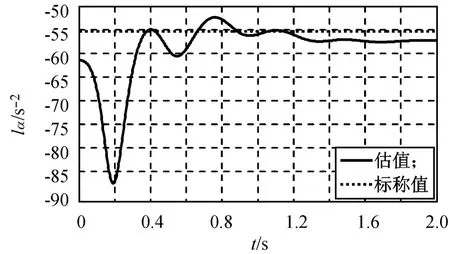
图12 lα的估计结果Fig.12 Uncertain disturbance estimation of lα

自适应滑模过程中对不确定参数的估计过程如图12所示。本文仅考虑法向力系数的不确定性,故仅需对lα[式(15)]进行估计即可。设真实系数较标称系数小10%,当lα的标称值为-61.428 1 s-2时,真实值为-55.285 3 s-2。令初始时刻lα的估值等于标称值,则最终的估值为-57.281 5 s-2,表明采用自适应估计后有效补偿了参数不确定性的影响。

4 结束语

本文基于动力学分析,建立了一适于姿态控制系统设计的模型。将俯仰通道的飞行控制系统设计分解成活动质量体位置伺服控制系统和姿态角跟踪控制系统两部分,用滑模控制理论设计控制律,设计中引入自适应项补偿参数不确定性的影响。在考虑参数不确定性条件下对综合单通道的飞行控制系统进行了仿真。结果表明：系统输出对指令的跟踪性能良好,自适应项能有效补偿参数不确定性的影响,具较强的适应能力,伺服驱动力保持在合理的范围之内。

[1]ROBINETT R D III,STURGIS B R,KERR S A.Moving mass trim control for aerospace vehicles[J].Journal of Guidance,Control,and Dynamics,1996,19(5)：1064-1070.

[2]BYRNE R H,STURGIS B R,ROBINETT R D.A moving mass trim control system for reentry vehicle guidance[R].AIAA,96-3438.

[3]BA LARAM J B.Sherpa moving mass entry descent landing system[C]∥International Design Engineering Technical Conferences&Computers and Information in Engineering Conference.Long Beach,California：[s.n.],2005,DETC2005-85283：63-79.

[4]BYRNE R H,ROBINETT R D,STURGIS B R.Moving mass trim control system design[R].AIAA,96-3826.

[5]BYRNE R H,STURGIS B R,ROBINETT R D.A moving mass trim control system for reentry vehicle guidance[R].AIAA,96-3438.

[6]PETSOPOULOS T,REGAN F J,BA RLOW J.Moving-mass roll control system for fixed-trim re-entry vehicle[J].Journal of Spacecraft and Rockets,1996,33(1)：54-60.

[7]周凤岐,崔利明,周 军.弹道式导弹弹头变质心机动控制[J].宇航学报,2000,21(增刊)：107-110.

[8]李瑞康.变质心控制与预测制导在飞行器再入机动中的应用研究[D].哈尔滨：哈尔滨工业大学,2009.