防空导弹弹性振动抑制

许 龙,余祖铸

(上海精密仪器研究所,上海 200233)

0 引言

防空导弹的弹体结构常有细长的外形并采用气动力控制其机动,其弹性振型的频率相对较低。在控制力和惯性力作用下,弹体被激励产生弯曲模态,通常称为弹体的弹性振动。弹体的弹性变形经安装在弹上的陀螺等传感器感受并传递至伺服机构后,会导致控制舵面的附加输出,激发产生更大的弹性变形,使振动加剧,从而导致控制回路失去稳定,弹体结构被破坏。因此,在设计飞行控制系统时,需考虑对弹性振动进行抑制,在实测弹体弯曲频率处须获得适当的回路衰减。在防空导弹控制系统设计中,通常考虑弹体的一阶振动。本文对防空导弹弹性振动的抑制进行了研究。

1 弹体运动特性

有轴对称气动外形弹体的导弹,其俯仰和偏航方向的气动特性相同。如忽略滚动交链的影响,弹体的运动特性可用刚体和弹性体描述。

1.1 刚性弹体

在小扰动和线性化条件下,刚性弹体在俯仰和偏航方向的运动可用微分方程描述为

式中：ϑ0,θ,α分别为刚性运动的姿态角、弹道倾角和攻角;δ为舵偏角;n,v分别为刚性运动的过载和速度;a1～a5,为气动参数;g为重力加速度。

整理式(1)～(4),可得姿态角速度对舵偏角的传递函数

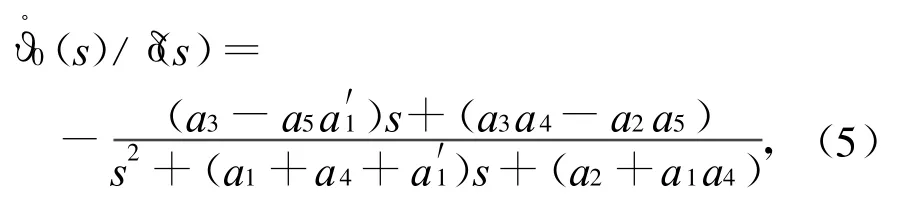
或表示为

式中：KC为弹体的传递系数;TC,ξC分别为弹体的时间常数与相对衰减系数;T1C为弹体的转弯时间常数;s为拉氏算子。

1.2 弹性弹体

弹体沿纵轴的弹性振动可用不同阶次的正弦振型描述,其参数由弹体的结构特性确定。防空导弹通常用一、二阶的振型,其中一阶振型的微分方程为

式中：q1为弹体一阶振型的广义坐标;ϑ1,n1分别为弹性振动引起的弹体姿态角的过载;D11,D21,D31分别为弹体阻尼、法向力及控制力弹性气动系数;ξ1,ω1分别为一阶振型的阻尼系数和角频率;,w1分别为一阶振型的斜率和位移。

在速率陀螺的安装处,由一阶弹性振型引起的弹体姿态角

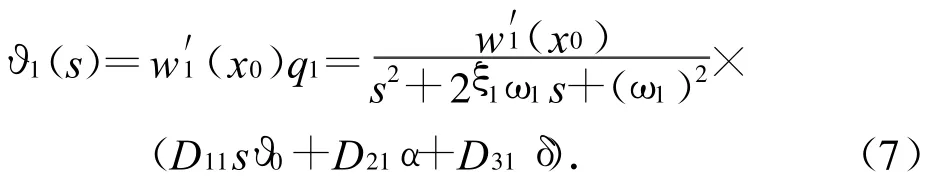
考虑弹体的弹性振动,则其姿态角满足关系

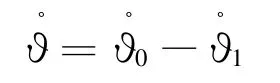
若忽略姿态变化对弹性振动的影响,则陀螺所敏感的弹体姿态角变化如图1所示。

图1 弹体姿态角Fig.1 Block diagram of body attitudeangle

2 飞行控制系统结构

采用无线电寻的制导的防空导弹多有角速率和加速度反馈的飞行控制系统,其组成如图2所示[1-2]。图中：WN(s)为结构滤波器的传递函数;KA为加速度反馈增益;KB为复合反馈增益;KE为角速率反馈增益;KI为积分控制增益。

飞行控制系统由角速率反馈、复合反馈和加速度反馈组成。角速率反馈构成的阻尼回路,其作用主要是增加弹体运动的阻尼,抑制弹体的弹性振动,从而稳定弹体的姿态运动;对速率陀螺输出进行积分提供复合姿态稳定反馈,主要用于对静不稳定的弹体进行稳定;加速度反馈的作用是使弹体的过载对控制指令的传递保持稳定的增益,同时改善过载的动态响应。

上述控制回路中,积分器对高频信号衰减很快,复合反馈和加速度反馈对弹体的弹性振动均不敏感。因此,对弹性振动的抑制主要研究阻尼回路的稳定性。

图2 飞行控制系统Fig.2 Flight control system

3 弹性弹体稳定性

在图2所示的结构中,阻尼回路的结构可简化成图3所示。图中：KW,TW,ξW分别为伺服机构的传递系数、时间常数和阻尼系数;KG,TG,ξG分别为速率陀螺的传递系数、时间常数和阻尼系数。弹体的频率特性如图4所示。

图3 阻尼回路Fig.3 Damping loop

由图4可知：弹体弹性振动的频率远高于刚性运动的自然频率。由于弹体弹性振动的阻尼一般很小(ξ1≤0.01),在一阶振型的频率处,其幅频特性有很高的峰值,相频特性则有-270°的相移。

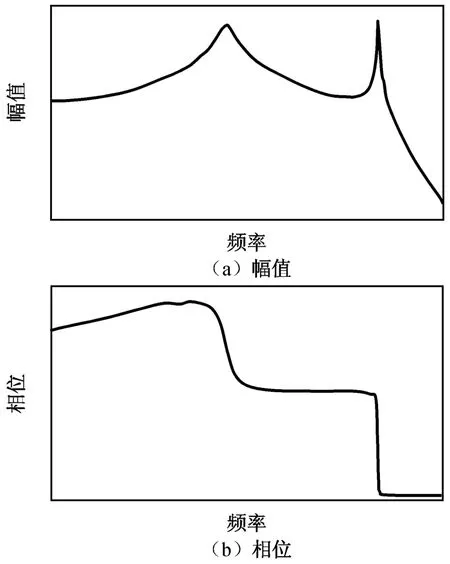
图4 弹体对数频率特性Fig.4 Bode plot for missile body

在设计控制系统时,为命中近界目标,希望增加阻尼回路的带宽,但带宽增大会引起弹体弹性振动的交链。如弹体弹性振动的频率小于阻尼回路带宽的6～10倍,就易使系统出现振动不稳定。

在图4所示的频率特性中,因弹性振动的峰值很高,故阻尼回路仅采用刚性反馈无法使弹性振动获得稳定。

设计阻尼回路时,可分别处理刚体运动控制和弹性振动抑制,即回路能按低频和高频两部分分别设计。刚性弹体姿态运动的稳定,主要是合理确定频带的宽度,对弹性弹体的稳定则可采取以下方法。

3.1 陷波补偿

在抑制弹体弹性振动的设计中,常用方法是在传感器与伺服系统间设计一有带阻滤波特性的校正网络,通常称为结构滤波器。结构滤波器为一深陷的“漏斗形”网络,在回路幅频特性一阶振型频率处产生大幅衰减,显著减小一阶振型频率处的峰值,使回路的幅频特性降低至零分贝线以下,在该频段上的正弦信号不能通过滤波器,从而实现抑制弹性振动。

理想结构滤波器网络的传递函数为

式中：ωN,ξN分别为二阶微分环节的角频率和阻尼系数;ωD,ξD分别为二阶惯性环节的角频率和阻尼系数。可选网络参数ωN=ωD=ω1,ξN=ξ1,ξD=0.5。此处：ω1,ξ1分别为一阶弹性振型的角频率和阻尼系数。

实际工程设计中,弹体的模型参数有不确定性,网络参数也可能随之而变,这些误差均会对回路的稳定产生影响。因此,设计滤波器时阻带须保持一定宽度,常取

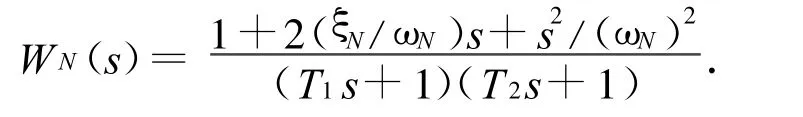
式中：T1,T2为时间常数。可选择合适的T1,T2以调整网络宽度,使回路对弹体弹性振动频率的变化有一定的适应能力。

对如图4所示的经结构滤波器衰减后弹体频率特性,其阻尼回路的频率特性如图5所示。

图5 阻尼回路对数频率特性Fig.5 Bode plot for damping loop

采用陷波补偿,使回路的幅频特性在一阶振型频率处产生大幅衰减,因而能使系统稳定。为适应弹体参数的变化,结构滤波器的设计有一定的频带宽度,但这会引入低频的相位滞后(图5中,采用的结构滤波器使回路的频率特性在剪切频率附近产生的相位滞后约20°),由此将会影响刚性运动的稳定性。为补偿低频的动态响应,可对回路的频率特性作适当校正。

3.2 相位稳定

根据经典控制理论的稳定性判据,闭环系统稳定的条件是系统开环幅频特性在大于零分贝的频率范围内,相频特性对-180°线的穿越应相差N/2次。此处：N为系统位于右半平面的实根数。

相位稳定的方法是通过选择系统的部件特性(如伺服机构),将回路的开环幅相特性产生一定的旋转,使其离开临界稳定的位置。这样,回路的相频特性在振型频率前快速下降并穿越-180°线,使-180°处对应的幅值处于零分贝线以下。

弹体与伺服机构的幅相特性如图6所示。

图6 弹体与伺服机构的幅相特性Fig.6 Nyquist plot for missile body with actuator dynamics

相位稳定的实质是改造弹体的频率特性。在幅相特性平面上,将系统的幅相特性沿顺时针方向旋转一定的角度,将其在-180°处的穿越转移到-270°处,从而使其在穿越过-180°线时相应的幅频特性位于临界点之内。

相位稳定的方法相当于增加补偿器的极点,使系统的根轨迹在引起一阶振型的极点处向左移动,增大对弹性振动的阻尼,从而稳定振幅的模态。

采用相位稳定进行回路设计,要求回路的剪切频率为转接频率的约1/3,且系统的相位裕度应大于30°。

3.3 增益稳定

增益稳定是通过在系统控制带宽外的频段设置额外的增益,减小对振动模态的激励。

采用的增益稳定方法是在执行机构与传感器间串联有低通滤波的校正网络,对振型频率处的幅值进行衰减,使伺服机构对弹性振动的信号不引起响应。典型低通滤波器的传递函数

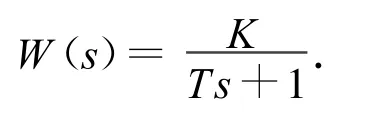
式中：K,T分别为滤波器的传递系数和时间常数。

引入滤波器后,阻尼回路频率特性的变化如图7所示。

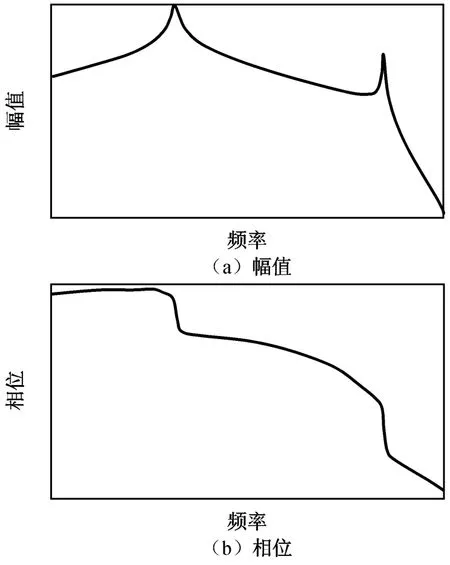
图7 引入滤波器的阻尼回路对数频率特性Fig.7 Bodeplot for rate loop with structural filters

滤波器的参数选择,应使峰值获得必要的衰减。

回路引入滤波器后,使高频部分的幅频特性得到了衰减,但同时也会使系统产生相移,影响系统的稳定裕度,在设计回路时需引入一定的相位超前。

高频部分的衰减降低了回路的增益,限制了回路的带宽,可使回路有较强的鲁棒性,并能防止高频噪声进入系统的工作频带,但同时会使系统的动态响应受到影响。

系统的反应时间与弹体特性和飞行状态有关。导弹在高空飞行时,空气动力变小,过载能力较低,同时弹体受激励后引起的弹性变形也相对较弱。因此,采用低通滤波器能衰减高频的峰值。

4 结束语

本文对防空导弹弹性振动的抑制进行了研究。采用频率响应分析,对系统的稳定性设计可用陷波补偿、相位稳定和增益稳定等方法,也能采用组合的方式。陷波补偿能有效衰减弹性振型的峰值,但参数的变化对回路的稳定性会产生影响;相位稳定可使回路有足够的频带;增益稳定有较强的鲁棒性,并能防止高频噪声进入系统的工作频带,但会使动态响应受到影响。设计回路时,应根据弹体的气动特性、飞行状态,以及回路的结构综合考虑。传感器的安装位置影响速率陀螺对弹性振动的响应。对一阶振型而言,选择靠近中间位置安装,可降低对弹性振型的灵敏度。

[1]NESLINE F W,NESLINE M L.Phase vs gain stabilization of structural feedback oscillations in homing missile autopilots[C]//1985 American Control Conference,Boston：AACC,1985,1：323-329.

[2]NESLINE F W,WELLS B H,ZARCHAN P.A combined optimal/classical approach to robust missile autopilot design[R].AIAA,79-1731.