基于改进AHP的低轨星座传感器调度方法
2011-09-18薛永宏
薛永宏,王 博,安 玮,徐 晖
(国防科学技术大学 电子科学与工程学院,湖南 长沙 410073)
0 引言
低轨星座能有效弥补高轨星座的不足,实现对目标的持续跟踪。但由于卫星和目标高速运动且传感器视场有限,通常单个传感器无法实现对目标的全程持续跟踪,因此需要使用高效传感器调度技术对传感器资源进行合理分配。传感器调度的目的是在合适的时候选择合适的传感器对合适的目标提供合适的服务[1]。传感器调度是在系统特定的约束前提下,根据一定的优化准则,对有限的传感器资源进行科学合理分配,以达到系统的最佳性能。
层次分析法(AHP)通过量化供选择的各因素进行排序的一种决策方法[2]。随着AHP的广泛应用,其中依据人主观经验构造判断矩阵的非一致性问题逐渐成为关注的焦点。为消除判断矩阵非一致性,提出了多种判断矩阵构造方法的改进措施[3-4]。针对低轨星座对目标持续跟踪这一特殊应用背景,文献[5]应用AHP法,通过计算传感器对目标的配对权值向量,对传感器资源进行调度,但该方法需对判断矩阵进行一致性检验,同时还存在调度时间间隔短、调度频繁等缺点。为此,本文通过改进AHP判断矩阵的构造方法,建立相应的优化准则,提出了基于改进AHP(IAHP)的传感器调度方法。
1 优化目标分析
传感器调度的主要目的是依据一定的准则,科学合理地分配传感器资源,以期实现对目标的高精度持续跟踪,因此跟踪精度是主要的优化目标之一。在传感器调度过程中,由于不能预知未来一段时间内跟踪精度的变化趋势,当前时刻选择的传感器组合可为短时最优,但不一定是长时最优的选择,故将跟踪精度变化率也作为传感器调度的优化目标,以使当前选择的传感器组合有长时较优的效果。另外,考虑传感器资源的使用效率,本文将传感器组的预期跟踪时间也作为调度的优化目标。
1.1 目标跟踪精度
对目标进行立体跟踪定位至少需要2颗卫星,而求取双星对目标的跟踪精度需要卫星对目标跟踪误差的协方差阵,计算过程复杂。文献[6]分析了2颗卫星与目标间的几何关系对定位误差的影响,文献[7]将双站测角定位的误差作为多传感器调度的优化目标。为简化跟踪误差的计算,本文将目标与卫星间的几何关系转化到二维平面,整个系统可抽象为一个只测角定位系统。如图1所示。

图1 二维平面测角定位Fig.1 Two-dimensional angle measurement and location
二维平面内建立位置坐标系,设M(x1,y1),N(x2,y2)为两颗卫星所在位置,E(x,y)为目标位置;两颗卫星相对目标的观测角分别为θ1,θ2,则目标位置的估值
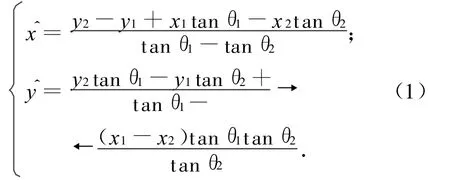
窄视场跟踪传感器的像平面与欧拉角测量误差在二维平面内均可等效为测角误差[8]。若仅考虑测角误差,则有
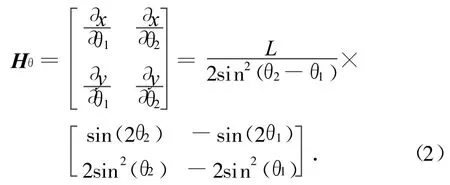
设两颗卫星的测角误差均为σθ,则跟踪协方差阵

而跟踪精度
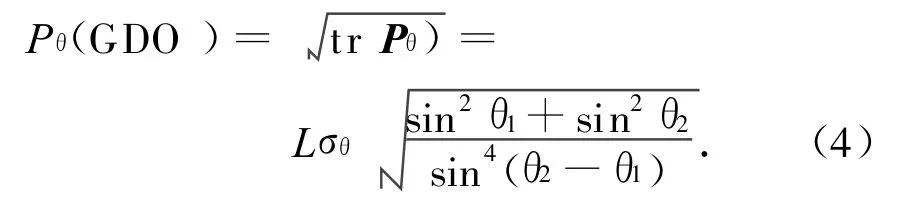
1.2 目标跟踪精度变化率
由式(4)可知:跟踪精度的变化依赖于L及2颗卫星对目标的观测角θ1,θ2。这3个参数都随目标、卫星相对位置而变,为时变参数。由其对时间的导数,可知跟踪精度的变化与目标、平台的速度有关,因此通过当前时刻平台、目标的位置及其运动速度就能获得跟踪精度的变化趋势。
在图1的二维平面坐标系中,设M(x1,y1)=M(0,0)为坐标原点,N(x2,y2)=N(x2,0),则L=x2,

另假设L2=,则跟踪精度的变化与E(x,y),N(x2,0)的移动速度相关。设E(x,y),N(x2,0)的移动速度分别为(vx,vy),(,0),可得θ1,θ2,L对时间的导数分别为

进而得跟踪精度变化率
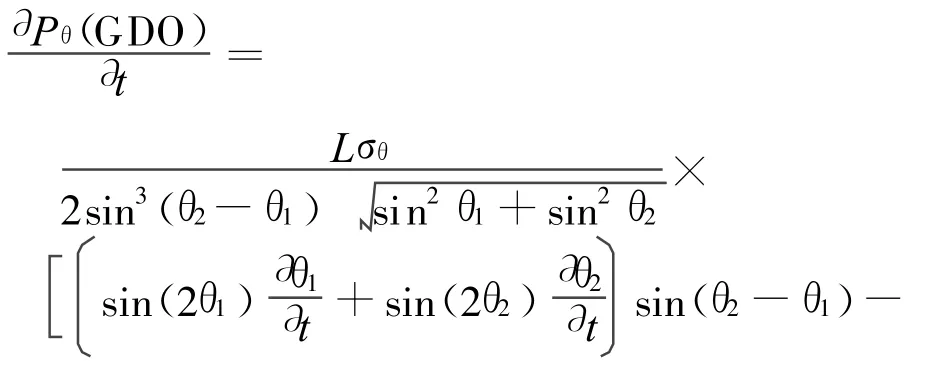

1.3 预期跟踪时间
预期跟踪时间tp是指从当前时刻起,可实现有效覆盖的传感器组合(亦称伪传感器)对目标持续跟踪的最大时长[9]。伪传感器的预期跟踪时间与其对目标的覆盖有关,一定程度地反映了伪传感器的跟踪能力,伪传感器的预期跟踪时间越长,表示其跟踪能力也越强;传感器交接过程中将优先选择跟踪能力较强的伪传感器对目标进行跟踪。由于过短的预期跟踪时间可能导致系统频繁的传感器交接,这显然不利于系统的实时实现,因此本文设定伪传感器的tp满足tp≥tmin(tmin为系统容许最小预期跟踪时间)。若某一伪传感器的tp<tmin,则不作为备选伪传感器。
2 改进AHP传感器调度方法
2.1 判断矩阵构造方法改进
根据层次分析法的一般步骤建立低轨星座传感器调度的层次结构如图2所示。

图2 层次结构Fig.2 Hierarchical structure
判断矩阵构造是层次分析的关键步骤。通常依据SATTY的九标度法建立判断矩阵,见表1[10]。
理想的判断矩阵应具备性质:aii=1;aij=1/aji;aij=aik×akj。但由于认识事物存在主观性和模糊性,使判断矩阵一般不满足第三条性质,即不具备完全一致性。尤其对四阶以上的判断矩阵,该现象出现更频繁。这时,需检验判断矩阵具备一致性的程度(CR)[10]。当CR小于0.1时,可认为判断矩阵具满意的一致性,否则就需对原判断矩阵重新进行调整。在低轨星座的传感器调度过程中这种调整意味的是增加无效计算而极大影响计算结果的实时性,严重时会导致目标丢失,因此要对其进行改进。

表1 1~9标度定义Tab.1 Definition of 1~9 scale
设所分析的元素集W=[w1w2… wn]T,首先依据W各元素相对上一层的重要性赋予相应的初值:若W中各元素具有一定的数值大小且具有相同的量纲,则每个元素的数值大小反映了相应元素的重要性,其初值用元素的数值大小表示;若W中各元素不具有相应的数值大小或相同的量纲(如图2中准则层各元素间不具有相同的量纲),则依据各元素对上一层的重要性递减顺序赋予从大到小的初值。
判断矩阵的构造步骤如下:
步骤a)找出最大值wmax=max{W}和最小值wmin=min{W},计算γtab=。
步骤b)计算第n个元素wn的贡献值

式中:符号[]表示取整。
步骤c)按步骤b)计算W中每个元素的贡献值,得到W对应的贡献矩阵C=[c1c2… cn]T。
步骤d)构造判断矩阵aij=ci/cj。
显然,对任意的i,j,k,aij==aik×akj,完全满足一致性要求,因此由本文方法求取的判断矩阵无需检验一致性。
2.2 调度准则及流程
当传感器的空间分布较分散(传感器间距与传感器目标距离相当)时,不同传感器调度算法优化结果的目标跟踪精度差异很小,仅仅追求跟踪精度最优会导致传感器交接过于频繁,不利于对目标的稳定跟踪[11]。实际应用中,针对不同的目标,传感器对目标的跟踪精度只需满足其特定的任务需求即可。设定完成目标跟踪任务所需的跟踪精度门限Plim(GDO),规定只有当传感器对目标的跟踪精度大于此门限时才进行传感器的调度交接,否则维持上一时刻的调度结果,这样可显著减少传感器交接次数,同时也缩短了调度所需时间。本文传感器调度方法的步骤如图3所示,具体如下。
步骤a)判断时刻t跟踪传感器组St对目标的跟踪精度PGDO是否满足其任务需求,若不满足,则转步骤c),否则转步骤b);
步骤b)判断St的预期跟踪时间tp是否小于tmin,若是则转步骤c),否则得到时刻t+1的跟踪传感器组St+1=St,调度结束;
步骤c)应用层次分析法,重新选择时刻t+1的跟踪传感器组St+1,得到的St+1可与St相同,也可不同。

图3 传感器调度步骤Fig.3 Sensor scheduling steps
3 仿真
取星座轨道参数36/9/1/1237.5/77.5(包含分布在9个轨道面相位因子为1的36个卫星,卫星轨道高度1 237.5 km,倾角77.5°)[5]。目标发射点为东经125.91°、北纬39.40°,落点为东经120.60°、北纬43.00°,目标远地点高度2 100 km,发射120 s后进入中段飞行。通过50次Monte-Carlo仿真,分别用AHP,IAHP传感器调度方法对传感器资源进行调度,仿真所得整个过程目标跟踪的位置误差和速度误差分别如图4、5所示,详细结果见表2。注:定义速度收敛时间为速度误差首次小于2 m/s的时间,位置收敛时间为位置误差首次小于100 m的时间。
仿真结果表明:改进AHP方法有效减少了目标跟踪位置误差和速度误差的收敛时间;最小调度间隔也满足调度任务需求,且在整个交接调度过程中,传感器调度次数较少,保证了系统对目标的稳定跟踪。

图4 两种方法对应的跟踪误差(调度全程)Fig.4 Tracking error of two different methods(wholeprocess)
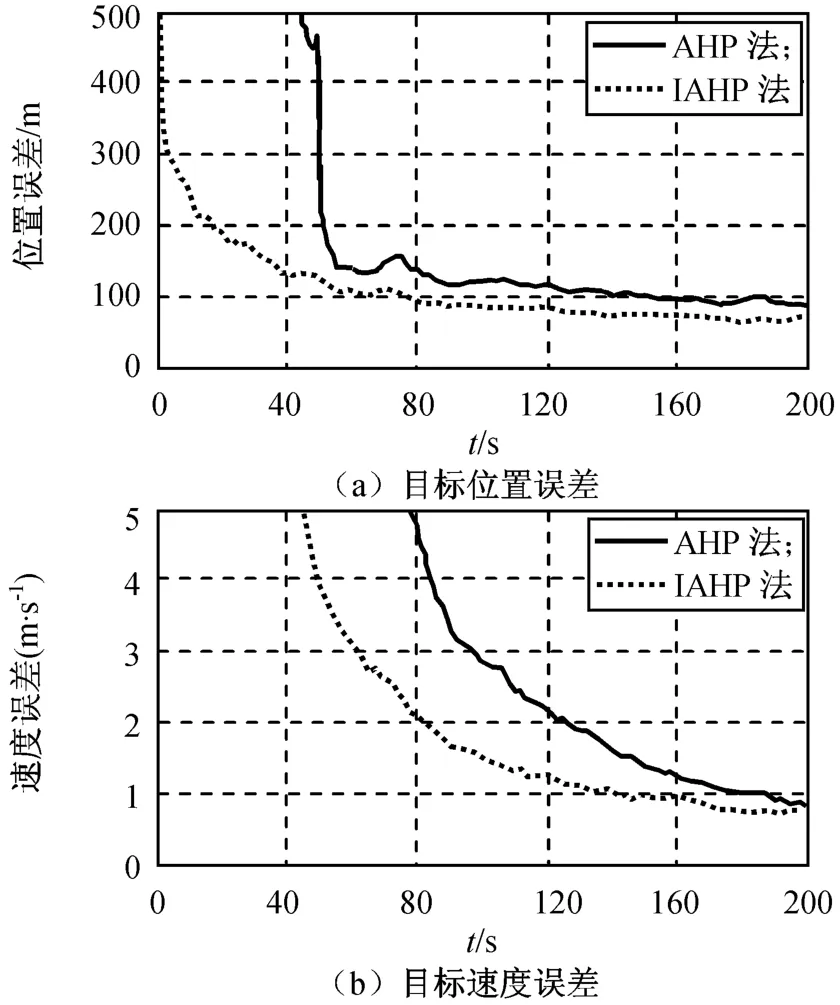
图5 两种方法对应的跟踪误差(初始200 s)Fig.5 Tracking error of two different methods(initial 200 seconds)

表2 两种方法调度结果对比Tab.2 Results confrontation of twodifferent methods
对多目标的传感器调度需考虑传感器资源冲突的解决机制,因此该方法不适于对多目标的传感器调度。
4 结束语
本文分析了影响低轨星座传感器调度的因素,引入参数跟踪精度变化率以克服传感器调度的结果仅满足短时最优的缺点;通过改进判断矩阵的构造方法,避免了传统层次分析中判断矩阵非一致性;通过建立调度的优化层次结构和优化准则提出了基于改进AHP的传感器调度方法。典型场景的仿真结果表明:本文的IAHP传感器调度方法能对低轨星座的传感器进行有效管理调度。
[1]XIONG N,SVENSSON P.Multi-sensor management for information fusion:issues and approaches[J].Information Fusion,2002,3(2):163-186.
[2]SATTY T L.The analytic hierarchy process[M].New York:McGraw Hill,1980.
[3]WANG T C,CHEN Y H.Someissues on consistency of fuzzy analytic hierarchy process[C]//Proceeding of the Fifth International Conference on Machine Learning and Cybernetics.Dalian:[s.n.],2006:1818-1822.
[4]BAO Y D,WU Y P,HE Y,et al.An improved AHP method in performance assessment:The Fif th World Congress on Intelligent Control and Automation[C].2004:177-180.
[5]鲁建华,程洪玮,王 博,等.基于层次分析的STSS系统传感器管理算法[J].飞行器测控学报,2009,28(1):85-89.
[6]谢 恺.天基红外低轨星座对目标的定位与跟踪[D].长沙:国防科学技术大学,2006.
[7]KAMATH S,MEISNERE,ISLERV.Triangulation based multi target tracking with mobile sensor networks[C]//IEEE International Conference on Robotics and Automation.Roma:IEEE,2007:3283-3288.
[8]HE X,WANG Y,XIU G H,et al.Constellation of multisensors in bearing-only location system[J].Radar,Sonar and Navigation,IEE Proceedings,2005,152(3):215-218.
[9]卢 迪.基于交叉熵度量的传感器管理方法研究[D].哈尔滨:哈尔滨工业大学,2004.
[10]吴 翊,吴孟达,成礼智.数学建模的理论与实践[M].长沙:国防科技大学出版社,2002.
[11]谢 恺,韩裕生,薛模根,等.天基红外低轨星座的传感器管理方法[J].宇航学报,2007,28(5):1331-1336.
