低轨红外观测星座时空观测漏洞分析
2011-09-18易东云
刘 冰,李 冬,易东云
(国防科学技术大学 理学院,湖南 长沙 410073)
0 引言
低轨红外观测星座可用于观测空间中的低温目标。如美国正在研制的天基红外预警星座(如SBIRDS-Low,STSS)能对导弹的全程弹道进行跟踪,弥补了高轨预警卫星系统和雷达系统不能观察导弹中段的缺点[1-7]。对卫星星座覆盖率的传统研究多是对地观测的覆盖率,但因为低轨红外观测星座观测的是低温空间目标,需将太空作为背景,故应考虑对地面一定高程以上对空的覆盖率[8-9]。目前,对这种观测条件下的研究报道较少。文献[10]以SBIRS-Low星座为研究对象,对地平面以上一定高程球壳网格采点,判断每个点的可见性,通过统计仿真时间内可见点数,将可见点出现的总次数除以网格点总数和时间采样点数,计算了不同高程处的平均覆盖率,发现此星座仅在高程250 km以上的空间才能实现全覆盖。对我国上空高程100 km覆盖的研究表明,仿真时间内覆盖率为85%~100%。文献[11]提出了一种基于视函数的跟踪传感器覆盖率计算方法,各纬度采点数与纬度余弦成比例的方法进行采点,改进了等经度采点方法,使采点更均匀,但其本质与文献[10]中计算平均覆盖率相同。该文讨论了卫星轨道高度、轨道倾角、升交点赤经等参数对各星座的平均覆盖率、最大覆盖间隙和平均覆盖间隙等覆盖率指标的影响,认为对所研究的星座在高度500 km以上能实现全覆盖。上述研究均将对一定高程空域的平均覆盖率作为评价星座指标的基础,其优点是可评价星座整体覆盖性能,关注重点是星座的设计,在尽可能低的高程上实现全覆盖,但对不能全覆盖的空域,无法对其观测漏洞给出较精细的描述和研究,不利于描述星座在特定时间段内出现的具体观测漏洞(即在特定时域、特定空域出现的观测盲区)。在特定条件下,这些观测盲区可能成为制约系统性能的关键因素。为此,本文分析了空间观测漏洞的成因、形状、分布规律和时间域的变化规律,并基于具体星座计算了漏洞的大小、生命周期、分布范围和数量。
1 时空漏洞成因
1.1 跟踪传感器中段目标可见性模型
中低轨卫星的跟踪凝视传感器能以太空为背景观测空间中的低温目标。本文中讨论的可见性指关注空域中的某点和星座中的某个或某些卫星几何上具有可观测到的条件。
由文献[12]可建立模型:设预警卫星的观测模式如图1所示。图中:H为卫星轨道高度;Re为地球半径;E为跟踪传感器俯仰方向活动范围,水平方向可360°旋转;γ为俯仰范围的下边沿切地角;L为传感器最大成像距离;l为卫星至目标的距离;S为卫星;M为目标位置;O为地球球心。则卫星可见的条件可表示为
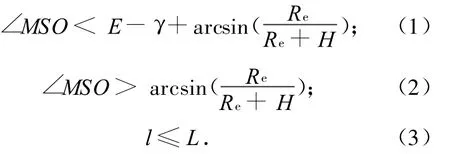
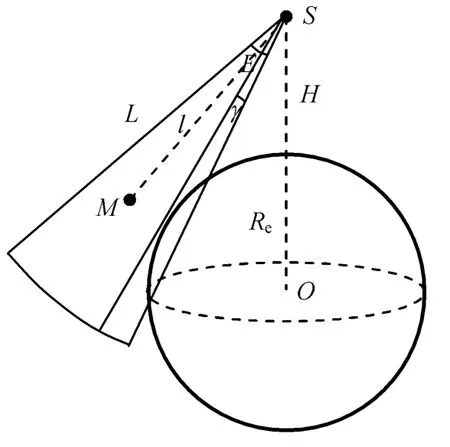
图1 可见性判断模型Fig.1 Visibility determination model
1.2 单星漏洞与星座漏洞
跟踪传感器针对低温空间目标观测时只能以太空为背景,因此某时段内,关注空域中存在某些区域对观测星座中的卫星是不可见的,即所谓漏洞。在传感器对目标的可视距离无限制的条件下,单星S的覆盖区域为图2(a)中阴影部分绕SO一周所得旋转体。
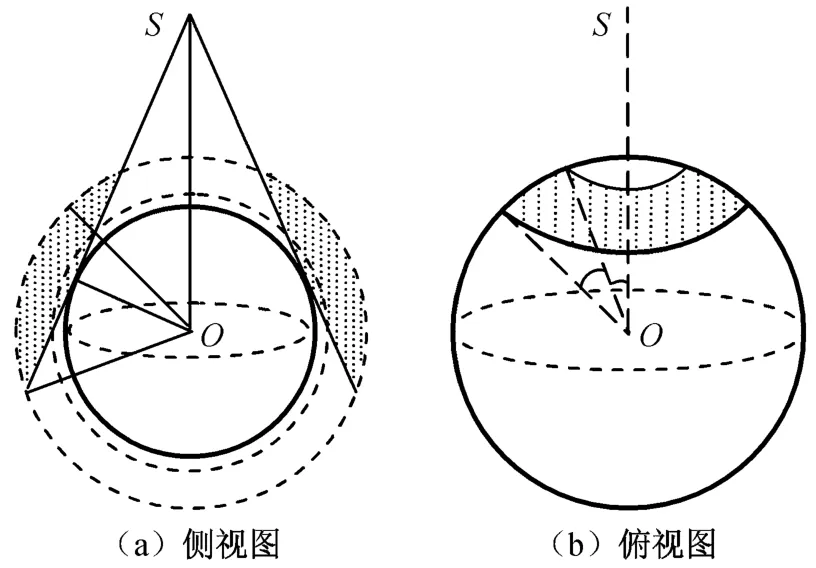
图2 单星覆盖区域Fig.2 Coverage of singlesatellite
由图2可知:单星的漏洞区域包含两部分,一是本星下方以地球为背景的区域(星下黑),另一是视线被地球遮挡的部分。星座的漏洞是所有卫星漏洞区域的交集。如图3中S下方的部分即是由这三颗星形成的漏洞区域。
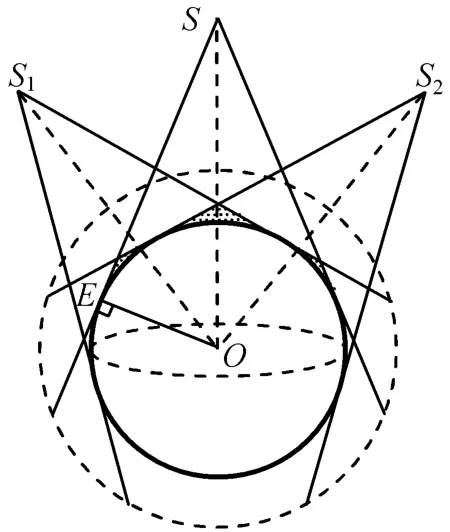
图3 多星形成漏洞Fig.3 Gaps due to multi-satellite observation
2 漏洞特性定性分析
2.1 漏洞体形状
漏洞体是星座中每颗星按图2(a)进行覆盖时各阴影区均未覆盖的部分。漏洞体是一个上小下大的类锥体,其底部为星座中所有星[如图2(b)]的覆盖圆环均未覆盖的部分,顶部为多条弧线棱形成的顶点或多个弧面交成的脊线,如图4所示。
由仿真计算可得某时刻36/3/1的Walker-δ星座的漏洞高程分布如图5所示。由图可知:漏洞分布如同山峰。
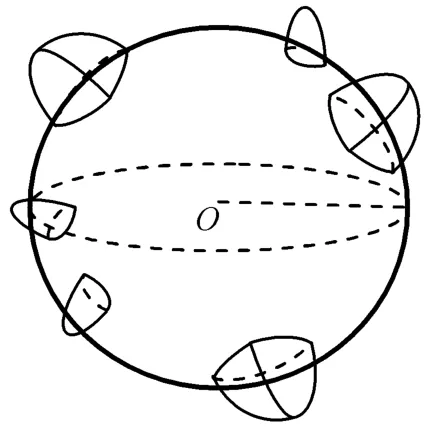
图4 漏洞示意Fig.4 Rough sketch of gaps
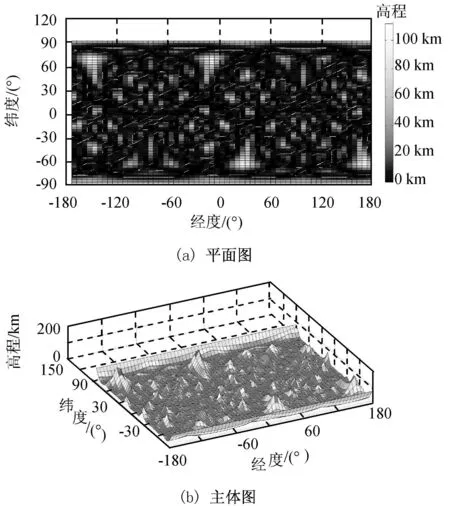
图5 仿真计算的漏洞Fig.5 Computed gapsby simulation
2.2 漏洞变化周期
因为卫星的运动,漏洞在不断产生、消失、变形和移动。如忽略地球自转,漏洞体的变化主要源于异轨星间相对距离的变化。因此,整个星座的漏洞时空分布变化周期应即为星座几何构型的变化周期
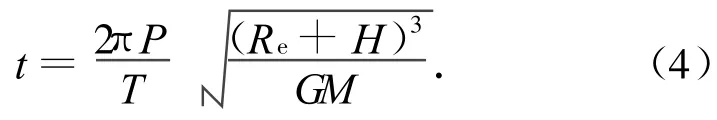
式中:P为轨道数;T为卫星总数;G为万有引力常数;M为地球质量。
3 漏洞指标定量分析方法
3.1 漏洞活动范围
对一个特定高程球壳上的点作离散化,如用天球的经纬度网格取点,就可不考虑地球的自转,则可见性可用矩阵A(t)=[aij(t)]表示。此处:aij(t)为时刻t某点的可见性,不可见时aij(t)=1,可见时aij(t)=0。漏洞活动范围可用矩阵表示。此处:t为1个重复周期内的离散化时间,且t=1,…,n。其中:n为在重复周期内时间采样点数。则B中每个元素的数值表示该点在1个周期内不能被观测的时间长度占周期的比例,不为0的点表示有漏洞经过,为0的点表示无高程高于关注空域下限的漏洞经过。
3.2 漏洞数
计算漏洞随时间变化规律时,对所有被判定为不可见的点进行聚类,将处于相同漏洞中的点归为一类,从而获得漏洞数。
本文采用作者设计的基于线性相关性的聚类方法。在特定时刻,若有n个空间采样点被判断为不可见,则每个采样点可用n维向量ηi(i=1,2,…,n)表示。聚类步骤如下。
步骤b)检查所有不可见点在空间位置上是否相邻,若不可见点i,j相邻,则令
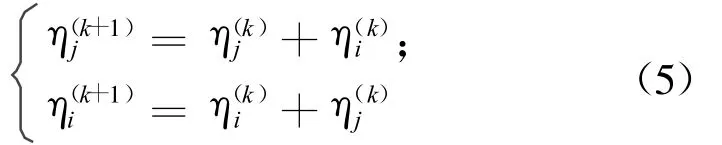
以更新ηi,ηj,迭代N次(k=1,2,…,N),相邻的不可见点对应的向量被更新为线性相关的向量。
步骤c)计算向量间的线性相关性
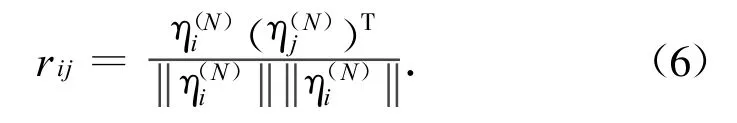
式中:||||表示取向量的模。
步骤d)设定适当的关联性检测阈值r,若rij>r,则判断不可见点i,j在同一漏洞区域中;若小于阈值,则表明两点不相邻,不在一个漏洞区域中。从而可对所有不可见点聚类,算出漏洞个数。
3.3 漏洞大小
因漏洞形状并不规则,故漏洞大小可用漏洞在关注空域下限的底面积粗略衡量。将各离散点的可见性判断结果进行聚类,将属于同一漏洞的点放在一起,每点对应经度和纬度两个数值。设纬度和经度的采样间隔分别为δB,δL,则漏洞中的采样点(Bi,Li,Hi)可代表纬度为(Bi-δB,Bi+δB)、经度为(Li-δL,Li+δL)的一漏洞区域,该区域的面积
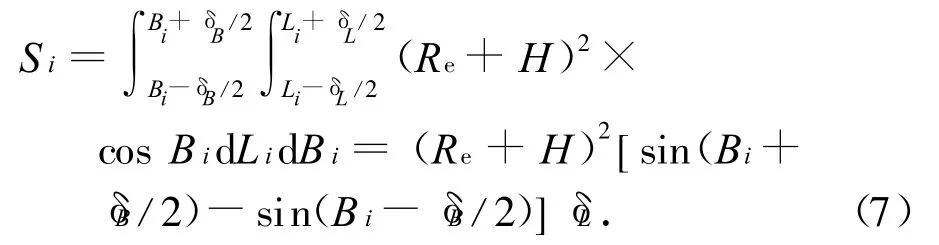
漏洞面积

4 仿真与分析
因星座中卫星数,卫星轨道高度、倾角,跟踪传感器作用距离,星座构型对时空漏洞均有影响。考虑前四个因素与星座部署成本密切相关,故选用构型不同但前四项参数相同的星座(星座部署成本相近),而时空漏洞特性仅受星座构型的影响。设卫星总数为36颗,选择较有代表性的轨道面数3,4,6作为研究示例,即选用A星座(36/3/1)、B星座(36/4/1)、C星座(36/6/1)三个Walker-δ星座进行仿真。
4.1 漏洞活动范围
仿真所得三个星座高程75 km以上漏洞的活动范围分别如图6~8所示。图中的亮色区域为漏洞经过处,颜色越亮表示漏洞在此处驻留时间越长。由图可知:每块亮色区域不相交,均孤立存在,说明漏洞的活动区域有限,且不会移动到其他漏洞曾占据的空域;漏洞的分布在南北半球呈现一定的对称性分布;以上星座在中纬度地区都出现了大块的漏洞区域,且大块漏洞的高程上限也较大;可出现大块漏洞的区域数量为卫星轨道数的2倍;图5(a)仅是某时刻的漏洞分布图,南北半球各出现2个大漏洞,图6表明在1个周期内,南北半球会出现3个大漏洞,说明这些大块的漏洞区域并非同时出现或达到最大,而是交替出现。
4.2 漏洞数
仿真所得三个星座的漏洞数见表1。由表可知:从高程50~75 km,漏洞数急剧减少,高程50~75 km范围为漏洞多发区域,而高程大于100 km的漏洞是部分星座的主要大漏洞;根据漏洞数评价星座,A星座优于B星座,而B星座优于C星座。

图6 A星座高程75 km以上漏洞变化范围Fig.6 Activeregions of gaps higher than 75 km for constellation A
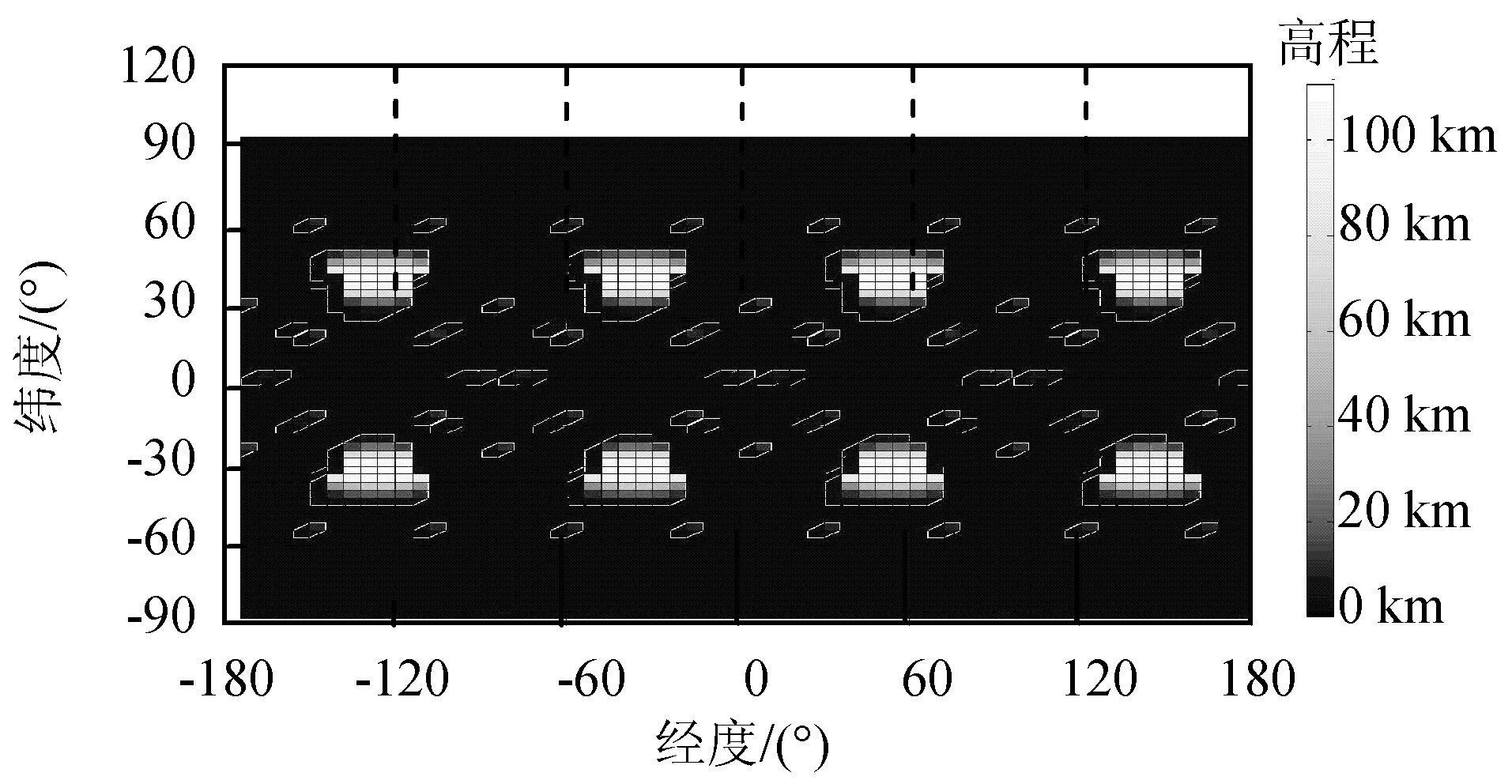
图7 B星座高程75 km以上漏洞变化范围Fig.7 Activeregions of gaps higher than 75 km for constellation B
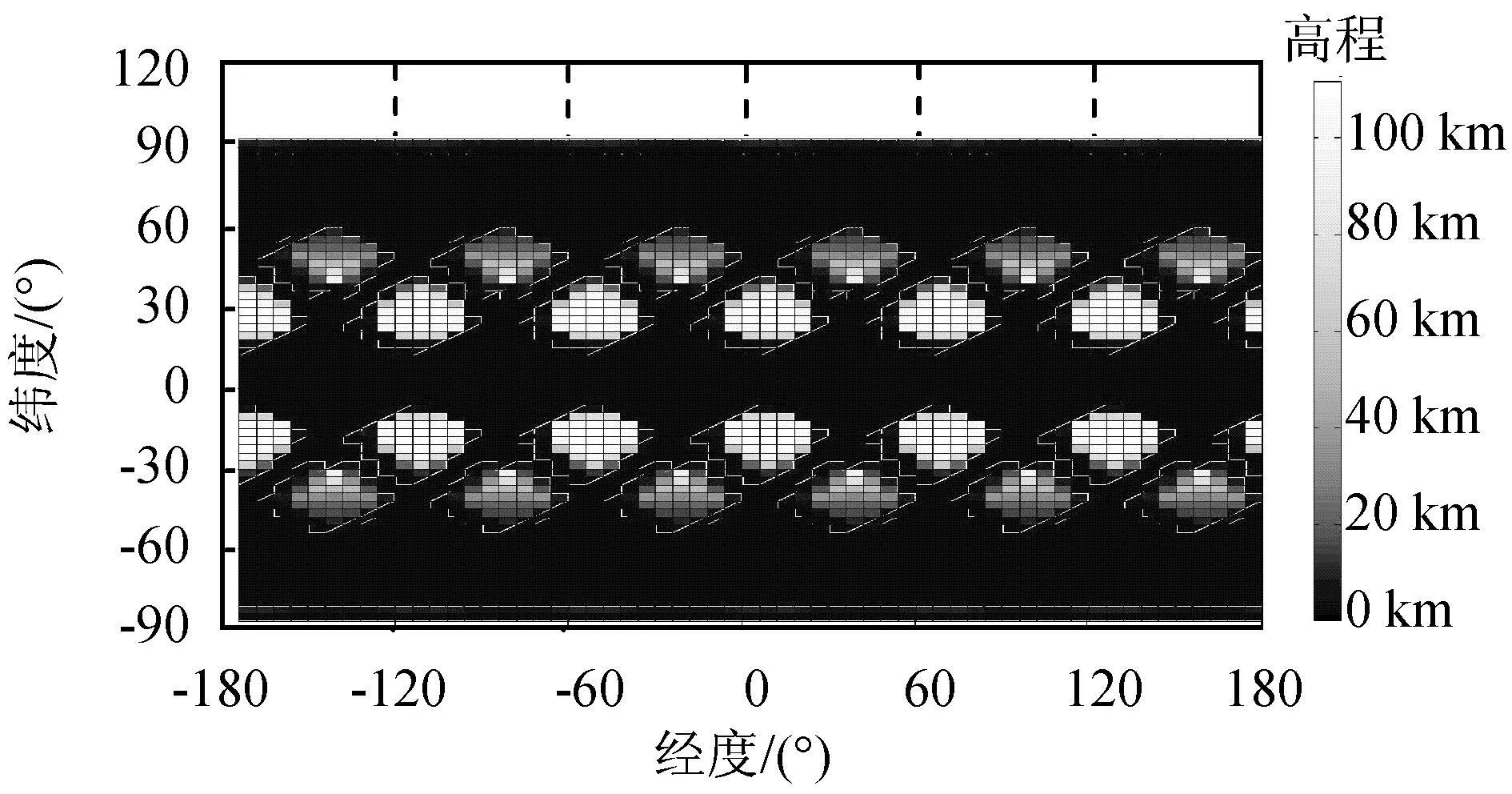
图8 C星座高程75 km以上漏洞变化范围Fig.8 Activeregions of gaps higher than 75 km for constellation C
4.3 漏洞大小
仿真所得不同时间三星座的漏洞面积分别如图9~11所示。由图可知:A,B星座的单个大漏洞的活动周期小于轨道重复周期,C星座的大漏洞活动周期基本等于轨道重复周期;星座A的漏洞小于星座B,星座B的漏洞小于星座C。
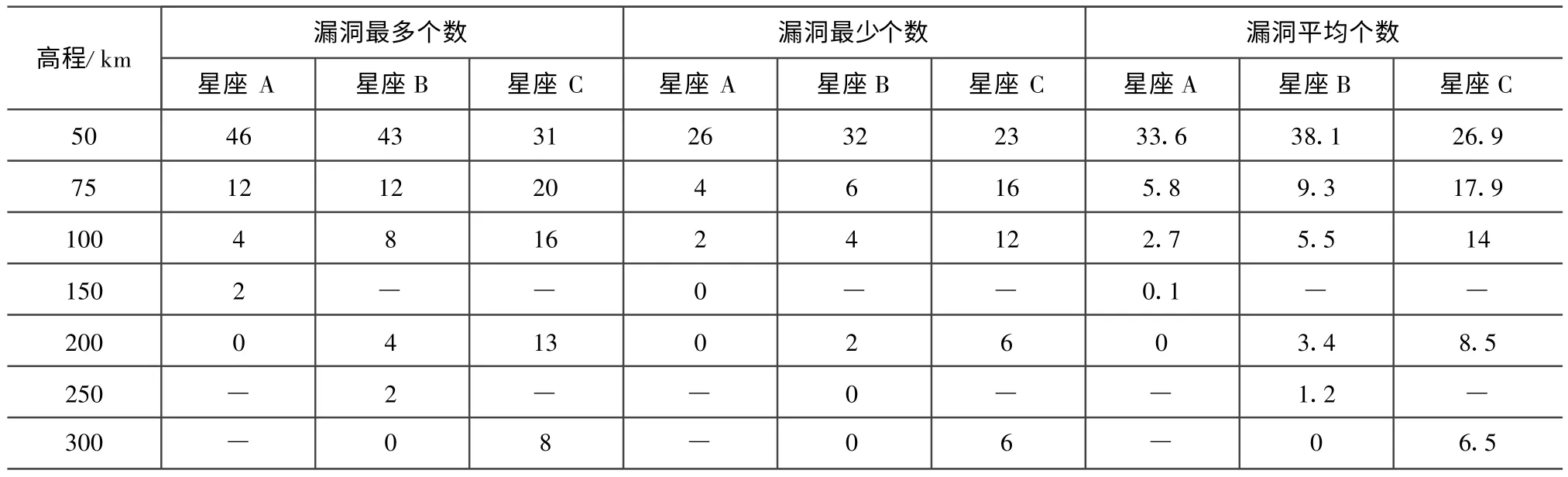
表1 仿真所得不同高程处三星座漏洞数Tab.1 Number of gaps abovedifferent altitude of constellation A,B and C
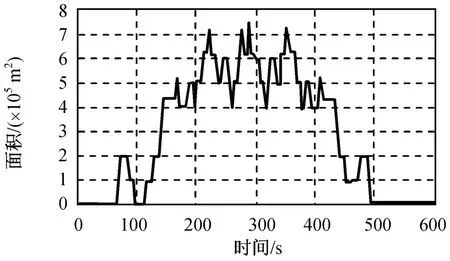
图9 高程75 km处A星座漏洞面积Fig.9 Area variation of a papitular gap higher than 75 km of constellation A
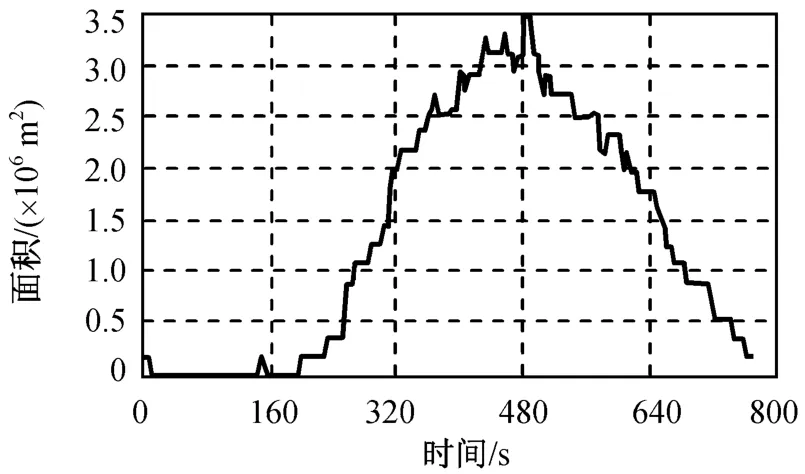
图10 高程75 km处B星座漏洞面积Fig.10 Area variation of a papitular gap higher than 75 km of constellation B
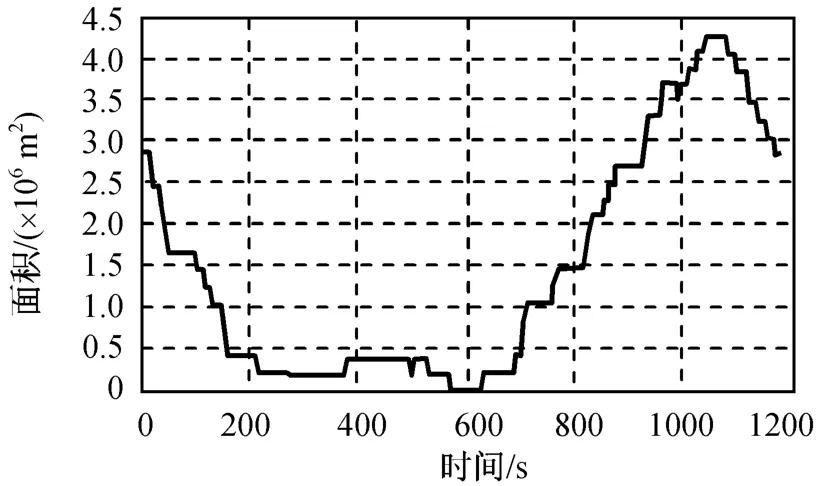
图11 高程75 km处C星座漏洞面积Fig.11 Area variation of a papitular gap higher than 75 km of constellation C
综合仿真结果,根据漏洞数、漏洞大小和漏洞活动范围,三个星座的从优到劣的排列顺序为A,B,C。
5 结束语
本文提出了低轨观测星座观测漏洞概念,分析了漏洞的成因、形状和变化周期,给出了漏洞活动范围、数量和大小的计算方法。仿真发现不同漏洞的活动范围不会交叠,漏洞活动范围的分布呈现南北对称,大型漏洞的个数是Walker-δ星座轨道数的2倍。可用漏洞数、漏洞活动范围、大型漏洞的活动周期及大小等对特定星座的性能进行评价。本文研究对低轨红外观测星座的设计有一定的指导意义。
[1]ANDREAS N S.Space-based infrared system(SBIRS)system of systems[C]//Proc of 1997 IEEE Aerospace Conference.New York:IEEE Press,1997:429-438.
[2]SLATTERY J E,COOLEY P R.Space-based infrared satellite system(SBIRS)requirements management[C]//Proc of 1998 IEEE Aerospace Conference.New York:IEEE Press,1998:223-232.
[3]BUDIANTO I A,OLDSJ R.A collaborative optimization approach to design and deployment of a space based infrared system constellation[C]//Proc of 2000 IEEE Aerospace Conference.Piscataway:IEEE Press,2000:385-393.
[4]WATSON J,ZONDERVAN K.The missile defense agency's space tracking and surveillancesystem[C]//Proc of Sensor,Systems,and Next-Generation Satellites XII.Bellingham:SPIE Press,2008:24-28.
[5]TANG S X,YI X Q,LUO X S.Research on earlywarning detecting tasks re-scheduling and sensor resource allcotion strategy of mid-course maneuverable ballistic targets[C]//Proc.of 2010 Fourth International Conference on Sensor Technologies and Applications.Venice/Mestre,Italy:[s.n.],2010:357-362.
[6]CLEMONST MⅢ.Improved space target tracking through bias estimation from in-situ celestial observations[D].Washington DC:George Mason University,2010.
[7]侯振宁.美国天基红外系统SBIRS的发展现状[J].现代军用仪器与技术,光机电信息,2002(8):30-33.
[8]吴 瑕,周 焰,崔 健,等.导弹防御系统中红外光电识别技术分析[J].红外与激光工程,2009,38(5):760-766.
[9]崔金辉,张 伟.美国天基低轨红外系统中段目标探测方法分析[J].光电工程,2010,37(6):54-57.
[10]程伟民,程建民,吴世义,等.天基红外低轨系统覆盖性能分析:中国空间科学学会空间探测专业委员会第十八次学术会议论文集(上册)[C].中国空间科学学会空间探测专业委员会,2005:186-190.
[11]王 博,安 玮,周一宇.跟踪传感器空域覆盖性能分析[J].航天控制,2009,27(6):90-95.
[12]赵 砚,易东云,潘晓刚,等.基于天基光学观测的空间目标可见性分析[J].飞行器测控学报,2007,26(3):5-12.
