基于混合蚁群算法的掩星星座优化设计

崔红正,韩 潮

(北京航空航天大学 宇航学院,北京 100191)

0 引言

无线电掩星技术最早起源于天文学研究,20世纪60年代美国将此技术用于行星大气和电离层探测等研究[1-2]。GPS无线电掩星技术作为一门新型技术始于20世纪90年代初。掩星探测技术是指利用安装在低轨道卫星上的双频全球导航卫星系统(GNSS)无码接收机接收GNSS信息(现阶段是GPS信号,以后可能是Galileo信号或北斗二代导航信号),观测穿过地球大气和电离层的GNSS信号特征,用数字技术反演大气参数(大气折射率、大气密度、大气湿度、压力和温度垂直廓线等)和电离层参数(电离层电子密度、电离层闪烁)的技术。国内外关于掩星观测的研究主要集中于掩星观测数据的反演方法和精度的改进[1-3]。国外对掩星任务轨道设计的报道较少,国内对掩星任务的单颗卫星和星座的轨道设计研究仅是简单的单变量分析,且未对轨道参数和星座构型参数进行优化设计和合理分析[4-5]。

在LEO掩星计划中,整个系统的评价必须建立在有效的模拟设计基础之上。本文利用LEO轨道模拟系统,在考虑LEO与GPS的卫星几何关系以及掩星观测天线视场的条件下,对全球范围内的掩星事件进行了模拟。用变量分离法分别调整轨道高度h、轨道倾角i、升交点赤经Ω和近地点幅角ω,分析了单个轨道要素对掩星数和时空分布分辨率的影响,并依此确定变量取值范围,以全球或区域掩星数量以及时空分布分辨率为评价指标,并针对本优化任务改进的混合蚁群算法对轨道要素进行优化,另外研究了分离变量法和混合蚁群算法综合方法以获得优化的LEO星座。

1 掩星模型

1.1 掩星事件判据

掩星事件的判定,主要由掩星事件定义和用户方需求而定。按GPS无线电掩星技术原理,本文定义LEO,GPS卫星为可见,穿越大气层的行为发生了一次掩星事件。但在实际应用中,还需考虑用户方的需求,如发生在地表至高度80 km的掩星探测数据主要用于计算大气温度、湿度、密度等参数,发生在100～500 km的掩星探测数据主要用于反演电离层的相关参数。此外,对特定的低轨卫星还需考虑星载天线方向等约束,对LEO,GPS卫星则只考虑地球摄动力的影响[3]。

考虑工程实际,本文假定掩星事件发生的有效高度为地表至80 km或100～500 km,LEO卫星天线有水平40°和俯仰7.5°的角度限制。

1.2 掩星判据简化与几何模型

根据掩星事件的判定条件,作相应的工程简化。设其数学模型如下。

a)δmin为LEO到地面切线与地心矢量连线的夹角,δmax为LEO至高度80 km轨道切线与地心矢量连线的夹角,δ为RL2G与地心矢量的交角,且满足δmin≤δ≤δmax。

b)VL为低轨卫星的速度矢量方向,RL2G(V)为RL2G在平面VL上的投影,为RL2G(V),VL的夹角,GPS天线水平40°满足约束≤40°[4]。

c)俯仰角λL2G在地平为基准上仰15°范围内,即15°。

当同时满足条件a)、b)、c)时,即发生一次掩星事件。如图1所示。

图1 掩星判据的几何模型Fig.1 Geometry model of occultation criterion

1.3 掩星探测系统评价指标

掩星探测系统的评价指标主要由两部分。一是掩星事件发生的总次数,是评价掩星探测卫星星座的关键指标。考虑卫星轨道参数对掩星次数的影响,用卫星星座可大幅提高掩星事件的数量,因此寻求掩星事件次数最多的星座构型成为星座优化的主要目标。另一是掩星事件发生的时空均匀性。保证掩星事件在所观测区域上时间及空间的分布均匀,能有效提高观测效率,降低观测成本。其中主要考虑掩星事件随时间的分布在同一天的均匀性,并对全球的纬度带和经度带的位置分布具均匀性。

2 混合蚁群算法

蚁群算法(ACS)已被许多研究证明是一种有效的离散优化,其中求解许多问题的结果都优于遗传算法、退火算法等启发式随机搜索算法[6]。本文采用一种可优化离散变量和连续变量的混合蚁群算法。

对有约束的优化可用罚函数法将其转为无约束问题。任何一个连续变量优化都可通过变换而成为一个在[0,1]上的函数优化。

将变量分层,离散变量有bm个,则离散变量分为bm层,每i层有节点bimax-bimin个。连续变量有xn个分量,并要求自变量的每个分量均精确到小数点后d位,则变量可由xn×d+xn+1层的节点组成,且第1,d+2,2d+3,xn×d+xn+1层由1个标号为0的节点组成,其余层均由标号为0～9的10个节点组成。其中：第(k-1)×(d+1)+2至k×(d+1)层表示自变量的第k个分量(k=1,2,L,xn),其余层均为辅助层。解码时,对各分量对应的层分别解码。这样,每个变量分量的最后一位与下一个分量的第一位间都有辅助层隔开,故前一分量的末位不会影响后一分量首位,并实现了离散变量与连续变量的混合优化。

用本文改进的混合蚁群算法进行掩星单颗卫星轨道参数和星座构型参数优化的流程如图2所示。

图2 混合蚁群算法掩星优化流程Fig.2 Flowchart of optimization of occultation events

3 单颗卫星轨道优化

根据变量分离法逐个优化变量原则,本文取LEO卫星轨道参数为轨道高度、轨道倾角、近地点幅角和升交点赤经,同时还将比较中性大气层和电离层所发生的掩星事件结果[5]。

3.1 中性大气层和电离层的全球掩星次数比较

中性大气层的高度为距地表0～80 km,电离层的高度为距地表100～500 km。LEO卫星轨道参数的设置见表1。表中：e,M分别为偏心率和平近点角。轨道要素的变化对全球掩星事件数量的影响如图3～6所示。

由图3可知：全球掩星事件数随轨道高度增加而减少。因为轨道高度增加,轨道周期增大,LEO卫星与GPS卫星星座可见次数减少。轨道高度每增加100 km,全球掩星事件数减少约20次,且变化平稳。由图4可知：当i在0°～160°范围内增大时全球掩星事件数呈上升趋势,大于160°的i增大时全球掩星事件数逐渐下降,其中i≈90°时掩星事件次数变化较大。由图5可知：同一天内的全球掩星次数随升交点赤经增加而有增有减,属短期效应。由于摄动的影响,升交点赤经的长期效应为持平。由图6可知：近地点幅角变化对全球掩星次数的影响较小,且同一天内的全球掩星次数亦随近地点幅角增大而有增有减,但幅度小于升交点赤经的影响。总体而言,轨道要素对大气层、电离层掩星事件数的影响一致,因此本文仅讨论大气层内掩星事件。

表1 LEO卫星轨道参数Tab.1 LEO satelliteorbit parameters

图3 不同轨道高度的全球掩星事件数量Fig.3 Number of global occultation events with various orbit height

图4 不同轨道倾角的全球掩星事件数量Fig.4 Number of global occultation events with various orbit inclination

图5 不同轨道升交点赤径的全球掩星事件数量Fig.5 Number of global occultation events with various orbit longitude of ascending node

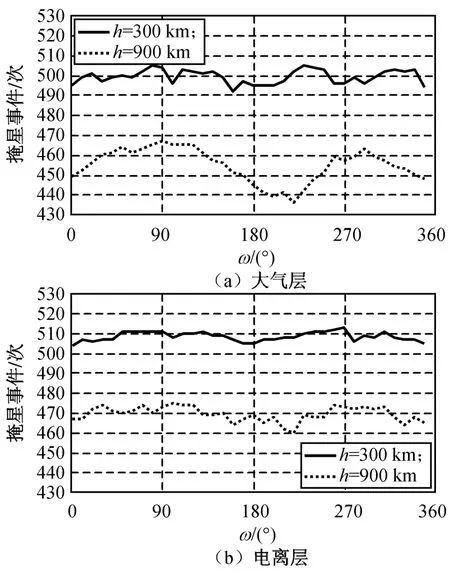
图6 不同轨道近地点幅角的全球掩星事件数量Fig.6 Number of global occultation events with various orbit perigee argument

3.2 轨道要素对全球掩星事件空间分布的影响

本文选取的LEO卫星轨道参数为轨道高度、轨道倾角、近地点幅角和升交点赤经,具体数值见表1。由同样方法,可得分析结果为：轨道高度、升交点赤经、近地点幅角对全球掩星事件沿纬度的分布影响较小;i=30°时掩星事件主要分布在纬度±30°的纬度带之间,i=60°时掩星事件主要分布在纬度±70°的纬度带之间,i=90°时掩星事件分布在全球,但低纬度地区分布较少,i=120°时掩星事件与i=60°类似,而i=150°与i=30°类似(仅掩星事件数略增);轨道高度、轨道倾角、升交点赤经和近地点幅角对全球掩星事件沿经度分布的影响较小。

3.3 轨道要素对全球掩星事件时间分布的影响

本文选取的LEO卫星轨道参数为轨道高度、轨道倾角、近地点幅角和升交点赤经,具体数值见表1。由同样方法,可得分析结果为：全球掩星事件时间分布呈波动趋势,且波动范围不大,波峰、波谷的位置与仿真开始时刻有关;轨道要素的变动对全球掩星事件时间分布的影响较小。

3.4 用蚁群算法优化

根据上述分析用蚁群算法进行优化时,对掩星事件次数考虑轨道高度和轨道倾角的影响;对掩星事件空间分布均匀性考虑轨道倾角对沿纬度带分布的影响;不考虑轨道要素对时间分布均匀性的影响;对全球掩星事件考察纬度-90°～90°纬度带;对中国区域的掩星事件考察纬度0°～55°的纬度带。

将纬度按间隔为5°分成纬度带,统计每个纬度带内的掩星事件次数NLatitude,计算各纬度带内掩星事件次数的方差D(NLatitude)。建立优化目标函数数学模型

式中：t为掩星时间;w1,w2为权重。取优化变量x=[h i],掩星事件参数优化的取值范围和结果见表2。

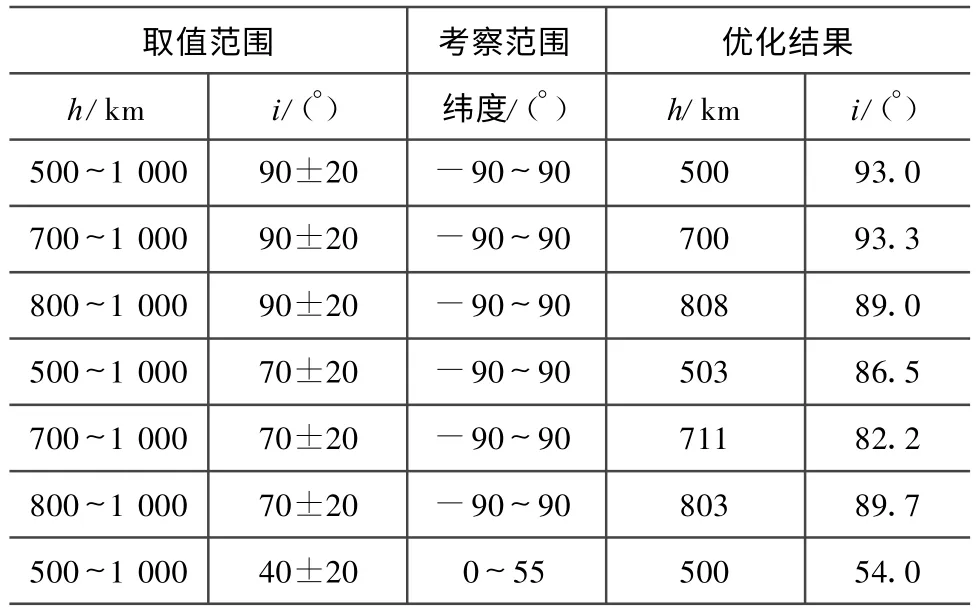
表2 LEO卫星优化结果Tab.2 Optimum result of LEO satellite

h=711 km,i=82.2°时,掩星事件在全球分布如图7所示;h=701 km,i=50.5°时,掩星事件在中国区域纬度带的分布如图8所示。

图7 全球掩星事件(h=711 km,i=82.2°)Fig.7 Global occultation events(h=711 km,i=82.2°)

图8 中国区域掩星事件(h=701 km,i=50.5°)Fig.8 Global and regional occultation events(h=701 km,i=50.5°)

4 卫星星座优化

满足一定任务要求的卫星星座构型设计是一个复杂的高不确定性寻优过程。除对卫星星座优化设计建立准确模型外,还需分析优化模型对寻优空间中各变量的敏感度,以降低寻优过程的不确定性和复杂度。由于掩星探测信号源GPS卫星星座采用对称的Walker星座,掩星任务轨道采用LEO圆轨道,则掩星星座的轨道采用LEO轨道,且掩星事件数量与时空分布均匀性仅受h,i变化的影响显著,据此,不失优化模型和方法的一般性,用Walker星座组成LEO掩星星座。确定Walker星座的构型参数为T,P,F,h,i,Ω0,θ0[7]。其中：T为卫星总数;P为轨道平面数;F为轨道平面间的相位因子;Ω0为第一个轨道面的升交点赤经;θ0为第一个轨道面的第一颗卫星的真近点角。又由于掩星事件的数量和分布特性受Ω,θ影响甚微,LEO星座与GPS星座间构型对称且具周期性的相对运动。因此,可将LEO掩星星座的Ω0,θ0设为常数。本文取星座卫星颗数Q=6(与COSMIC系统对比,COSMIC系统为玫瑰型星座,1个轨道平面仅有1个卫星)。

a)用分离变量法分析发现P,F对掩星事件数量以及在整个仿真时间内的空间分布均匀性和时间分布均匀性的影响甚微;

b)考虑掩星事件在同一时刻空间分布的均匀性以及星座的整体性能,选择P=6。

综上所述,本文采用的掩星星座优化模型满足约束

混合蚁群算法优化的初始参数、权值选值和优化变量的取值范围见表3[5]。研究区域分为全球和中国区域(纬度为0°～55°的纬度带),全球掩星优化结果与COSMIC系统接近。仿真发现：GPS接收天线的水平角和俯仰角约束对掩星产生次数的影响较小,仅影响单次掩星事件的持续时间。因此,本文优化结果可与COSMIC系统掩星次数统计结果比较。

表3 LEO掩星星座优化初始参数和优化结果Tab.3 Optimum initial parameters and result of LEO occultation constellation

仿真时间1 d,全球和中国区域的优化LEO掩星星座的掩星事件分布如图9、10所示。

由优化结果可知：优化方法可行,所得优化结果合理;全球优化结果与COSMIC系统的倾角取值有异,主要是因为COSMIC系统对南北两极的掩星观测需求不高。

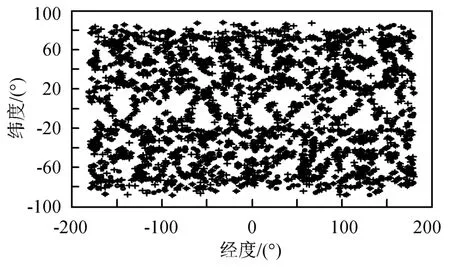
图9 全球掩星事件(F=1,h=813 km,i=84.3°)Fig.9 Global occultation events(F=1,h=813 km,i=84.3°)

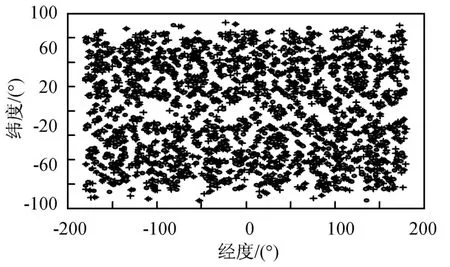
图10 中国区域掩星事件(F=2,h=802 km,i=54.1°)Fig.10 Global and regional occultation events(F=2,h=802 km,i=54.1°)

5 结束语

为服务于大气层和电离层探测,LEO卫星轨道和LEO星座设计要求实现掩星观测全球或区域分布均匀且数量尽可能多。本文用分离变量法研究了轨道参数对掩星事件的数量和时空分布的影响,用所得结论确定优化参数和取值范围;用混合蚁群算法获得了性能较优的轨道参数和星座构型参数。优化的结果与现有的掩星探测计划的轨道参数接近,表明本文研究方法正确。但本文尚存在局限性：掩星探测卫星一般具多用途,应考虑更多的约束进行优化设计;针对未来如Galileo,BeiDou-2等构型不对称的卫星导航星座,应进行构型不对称的非Walker星座进行构型优化设计;对掩星事件要进行更多的仿真计算,以发现更多规律。

[1]KUO Y H,ROCKEN C,ANTHES R A.Applications of GPS radio occultation data to weather and climateand theCOSMICmission[C]//Space200 4：Conference and Exhibit.San Diego,CA：[s.n.],2004：1-9.

[2]周义炎,吴 云,乔学军,等.GPS掩星技术和电离层反演[J].大地测量与地球动力学,2005,25(2)：29-35.

[3]肖业伦.航天器飞行动力学原理[M].北京：宇航出版社,1995.

[4]刘 琳.掩星探测系统卫星星座优化研究[D].北京：北京航空航天大学,2006.

[5]徐晓华,李征航,罗 佳.单颗LEO卫星轨道参数对GPS掩星事件分布和数量影响的模拟研究[J].武汉大学学报(信息科学版),2005,30(7)：609-612.

[6]陈 烨.用于连续函数优化的蚁群算法[J].四川大学学报(工程科学版),2005,36(7)：117-120.

[7]WERTZ J R,LARSON W J.Space mission analysis and design[M].Hawthorne：Microcosm Press,1999.