双参数威布尔分布在核电站数据处理中的应用

刘方亮，刘井泉，刘 伟

（1.清华大学 工程物理系，北京 100084；2.国家核电技术公司，北京 100029）

自1991年12月15日秦山核电站首次并网发电以来，我国核电已有近20年的运行经验。随着运行时间的增加，电站的系统、构筑物和关键部件（SSCs）等出现不同程度的老化退化问题，需制定相应的电站维修更换策略，以保证电站能长期安全、经济地运行。设备部件失效数据的处理是制定以可靠性为中心的维修（RCM）和寿期管理（LCM）等维修策略的基础。通过数据处理得到更准确的可靠性参数，是保证维修策略安全性和经济性的一个重要途径［1］。

国内电站设备的可靠性参数一般通过行业通用数据和电站自身失效信息的融合处理来得到。由于核电站的非能动机械部件具有较长的设计寿命，在对运行积累的故障记录进行处理的过程中会面临一些问题，例如失效样本过少、设备检查信息不能直接被利用、维修引起的可靠度变化等。目前采用的统计学处理方法会带来明显的系统误差，需要一种更为科学的方法进行处理。

本工作针对核电站失效数据处理过程中出现的问题，引入可修复系统模型和贝叶斯小样本方法，综合给出一种更为科学的处理核电站失效数据的流程。

1 核电厂常见设备失效数据

以国内某核电站定子冷却水泵机械密封为例，通过整理某核电站4个机组8台设备的工作票记录，结合设备投运时间等信息可得到表1所列的失效统计结果［2］。

同传统的可靠性试验数据相比，核电站运行积累的失效数据有以下3个特点：1）每次故障记录的起始时间不同、包含未发生故障的时间数据，单独通过故障间隔时间来处理会丢失一部分信息；2）某一设备可能记录到多次故障，需考虑故障间维修操作引起的可靠度变化而导致的数据分布不再独立；3）失效次数较少，表1共记录到9次故障，传统统计学方法可信度降低。

实际上，对于核电站大多机械部件，由于设计可靠度较高，现阶段运行积累到的失效数据均面临以上3个问题。

首先，为保留截止时未发生故障的时间信息，采用定时截尾试验的格式对失效数据进行整理；其次，为考虑维修带来的可靠度变化，引入可修复系统非齐次泊松过程（NHPP）模型［4］来处理数据的非独立性问题；最后，针对失效样本普遍较少的情况，采用目前较为成熟的贝叶斯方法进行处理［3］。进而综合给出了一种解决核电站失效数据中上述问题的方法。

2 失效数据的处理

2.1 定时截尾试验

定时截尾试验是可靠性试验的一种，失效信息可表述为 （n，r，t1，t2，…，tr，ts），其中：n为试验总体个数；r为发生失效的个数；t1，t2，…，tr为次序排列的失效时间；ts为试验截止时间。

由于核电站大多部件失效数据较少，采用定时截尾数据的格式可利用到截止时间信息，一定程度上扩大了样本容量。

将核电站现场失效数据按照定时截尾试验的格式来处理，需做以下近似：1）将每次失效作为单独的1次记录，认为这些数据服从同一寿命分布；2）假设每次故障起始时间相同，每次失效时间从零时刻开始到发生故障为止；3）合理选择1个截止时间，使其包含所有故障记录，同时认为运行时间大于它的记录未发生失效。

以表1中数据为例，观察其时间信息，取截止时间ts＝30 000h，此时有两组数据（30 504、31 368）大于30 000h，认为未发生失效，这样n＝11，r＝9。

同单独故障间隔时间信息相比，在上述假设条件下，样本大小由发生故障的9个扩充到11个（2个未发生失效），一定程度上利用原始信息扩大了样本容量。

2.2 可修复系统与数据趋势分析

某一部件运行过程中可能发生多次故障，进行维修或更换后部件的可靠度同初始相比会发生变化，故障间隔时间的分布不再独立。这时不满足修复如新的假设，通常采用的不可修复系统模型不再适用，需引入可修复系统模型进行处理。

常见的可修复系统模型包括：RP（Renewal Process）模型、HPP（Homogeneous Poisson Process）模型、BPP （Branching Poisson Process）模型、SRP（Superposed Renewal Process）模型和NHPP（Non－Homogeneous Poisson Process）模型。

D.M.Louit等［4］给出了一种采用数据趋势分析方法选择可修复系统模型的流程。针对表1中的数据进行趋势分析，得到的总试验时间曲线如图1所示。横坐标为第k次失效与总失效次数r的比值；用p（u）表示u时刻已发生失效的次数，则T（t）＝p（u）du为从0到t时刻总的试验时间。图1表明，失效率随时间的增加而增加，进而可确定定子冷却水泵机械密封失效数据服从NHPP模型。

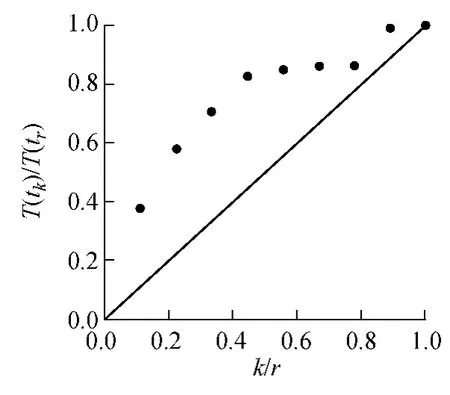
图1 机械密封故障数据总试验时间曲线Fig.1 Total time on test plot of mechanical seal failures

NHPP模型可用来描述设备的维修或替换未引起明显的设备可靠性变化（图2a）或发生单调变化（图2b、c）的情况。定子冷却水泵机械密封故障数据属失效率增加（图2b）的情况。

图2 3种常见失效时间分布趋势Fig.2 Three kinds of trends in time between failures

NHPP模型两种常见的失效率表达方法是幂率失效率（也叫威布尔失效率）和对数线性失效率［4］。

幂率失效率的表达式为：

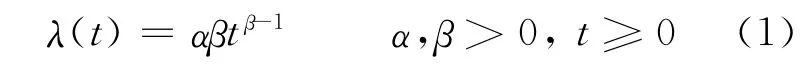
对数线性失效率的表达式为：

其中：α、β为待定值。

幂率失效率形式符合大多情况，其形式上等同于双参数的威布尔分布的失效率，因此，下面的计算采用双参数威布尔分布作为寿命分布来处理核电站失效数据。需指出的是，威布尔分布考虑了老化的影响，更符合机械部件发生老化退化的实际情况。

对于双参数的威布尔分布，其故障概率密度函数为：

其中：m为形状参数；η为尺度参数。

2.3 贝叶斯方法

由于核电站失效数据普遍较为缺乏，需考虑小样本的处理方法。小样本问题的特点是样本容量较少，传统的统计学方法不再适用。目前，国内外已发展许多解决小样本数据问题的方法，如由金字塔式方法延伸出的矩拟合的方法、Huang等提出的用于解决多元正态分布的多重替代法、基于贝叶斯原理的延伸算法、基于计算机仿真的Bootstrap和蒙特卡罗方法等［6］。其中，贝叶斯方法是处理小样本问题较为成熟的一种算法，可有效地综合多种来源、多种形式的先验信息，并根据电站运行情况进行数据更新。本工作选用贝叶斯方法来解决小样本问题。

贝叶斯公式是贝叶斯理论的基础，它可表示为：

记X＝（x1，x2，…，xn）为样本信息，θ为分布参数，上式中，f（x）＝∑f（x／θ）g（θ），为给定参数θ下xi的条件概率分布，称为似然分布。g（θ／x）为给定x时参数θ的概率密度分布，即后验分布。

对于服从威布尔分布失效数据，采用贝叶斯公式计算难以解析求解，考虑采用数值算法，计算过程如下。

1）根据失效数据和似然估计方程，得到Weibull分布参数的点估计和，参数极大似然估计的方程［5］为：

2）获取先验分布

对上步确定的威布尔分布参数和进行抽样，产生M组样本容量为n的Bootstrap再生样本［6－7］。对M组样本分别求解分布参数mj和ηj，然后假设mj和ηj相互独立，得到m和η的离散先验联合概率密度的M×M矩阵：

可得到，m＝mi，η＝ηj的概率为：

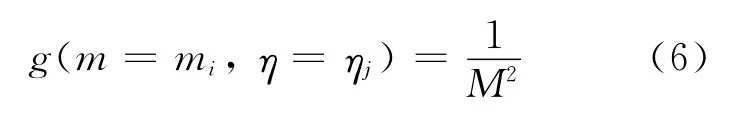
令其作为贝叶斯公式的先验分布g（θ）。

3）根据贝叶斯公式进行计算

条件下，样本的似然函数可表示为：

根据贝叶斯公式，经现场失效信息修正后的m和η得离散的联合验后分布：

根据式（8）可得到关于m和η离散的联合验后分布，求其全概率可得到所求的部件寿命可靠度分布函数：

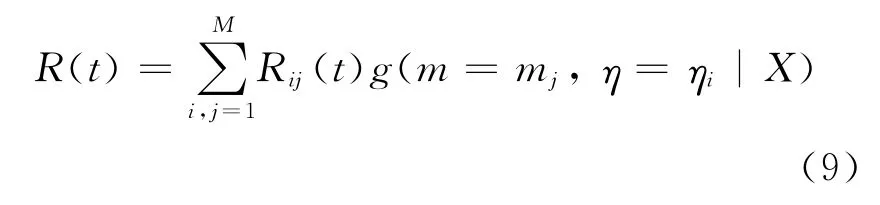
其中：Rij（t）＝

平均失效前的工作时间为：

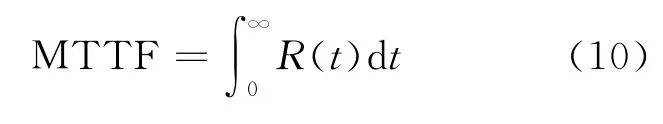
3 结果分析

定子冷却水泵机械密封的失效数据为：n＝11，r＝9，ts＝30 000h。失效时间由小到大依次为：3 312、6 432、7 224、7 896、12 288、15 216、17 664、17 736、18 048h。

由于双参数威布尔分布不存在共轭分布，原先假定的威布尔型寿命分布经贝叶斯公式修正后不再是威布尔分布的形式。其解析表达式较为复杂，用可靠度随时间的变化曲线表述，如图3所示。同文献［2］中结果的比较列于表2，MTTF可通过公式算出。

图3 可靠度函数曲线Fig.3 Plot of reliability function

表2 同拟合结果的比较Table 2 Comparison with data fitting

采用指数分布拟合得到的平均故障前的工作时间明显小于后两种方法的结果，这是因为指数分布的模型未考虑失效率的增加，直接拟合得到的失效率为某种意义上的均值，这使得评估结果在初期较为保守，而在末期可能出现危险。同时贝叶斯方法可看作是对失效数据抽样分布的修正，因此较直接采用威布尔分布拟合结果更接近电厂实际。同时本方法具有更好的适用性，可解决核电站数据处理过程中经常面临的样本较少、不能直接拟合的问题。

4 结语

本文给出了一种实用的处理核电站失效数据的流程，可用于解决失效数据处理过程中面临的分布不独立、样本容量少等问题。该方法通过将失效数据处理成定时截尾格式以保留部分检查信息，以双参数威布尔分布作为寿命模型从而避免了维修带来的可靠度变化的影响，最后通过引入Bootstrap抽样作为贝叶斯先验分布来处理威布尔分布小样本的问题，得到数值结果。

［1］SLITER G，CAREY J.Nuclear plant life cycle management implementation guide［R］.Palo Alto，USA：Electric Power Research Institute，1998.

［2］高纬光，刘井泉，刘鹏，等.发电机定子冷却水泵可靠性数据处理及分析［J］.原子能科学技术，2009，43（9）：828－833.GAO Weiguang，LIU Jingquan，LIU Peng，et al.Processing and analysis of reliability data on stator cooling pump［J］.Atomic Energy Science and Technology，2009，43（9）：828－833（in Chinese）.

［3］周法清.核电厂概率安全评价［M］.上海：上海交通大学出版社，1996：146－153.

［4］LOUIT D M，PASCUAL R，JARDINE A K S.A practical procedure for the selection of time－to－failure models based on the assessment of trends in maintenance data［J］.Reliability Engineering and System Safety，2009，94（10）：1 618－1 628.

［5］金星，洪延姬，沈怀荣，等.可靠性数据计算及应用［M］.北京：国防工业出版社，2003：42－45.

［6］金星，洪延姬.系统可靠性评定方法［M］.北京：国防工业出版社，2004：27－77.

［7］段晓军，王正明.小子样下的Bootstrap方法［J］.弹道学报，2003（3）：1－5.DUAN Xiaojun，WANG Zhengming.Applicability of Bootstrap method in small sample case［J］.Journal of Ballistics，2003（3）：1－5（in Chinese）.