几种典型车辆在斜拉桥桥面行驶的临界风速研究
2011-09-17韩万水刘健新李加武
马 麟, 韩万水, 刘健新, 李加武
(1.河海大学 土木系,南京 210098;2.长安大学 桥梁系,西安 710064)
21世纪的世界桥梁工程步入了建设跨海联岛工程的新时期,中国也开始了跨海工程建设。跨海大桥的建设带来交通便捷的同时,也带来了强侧风作用下桥面行车安全的问题。近年来,关于强侧风环境下桥面行车安全及其临界风速和车速的研究已有不少报道。桥面行车安全的研究涉及内容广泛,属于交叉学科:①复杂的风-汽车-桥梁耦合振动分析系统;② 驾驶员行为的数学模型;③ 行驶汽车的气动力测试。风车桥耦合振动的问题在铁路方面较早地进行了研究[1~3]。在公路方面,Guo、Xu[4],Chen、Cai[5],韩万水、陈艾荣[6],周立、葛耀君[7]都建立了风 -汽车 -桥梁耦合系统分析框架,但又各有侧重点。
在以往已经建立的风-汽车-桥梁耦合系统研究中,对车-桥的竖向耦合关系已考虑比较完善,但对桥面汽车的侧滑研究还不够完善。桥面汽车侧滑的研究需要在风-汽车-桥梁系统中考虑汽车的侧向自由度以及驾驶员行为的影响。在以往的相关研究中一些精细的车辆模型已经考虑了车轮的侧向自由度,但对驾驶员行为关注不够。Chen、Cai[5]率先对该问题进行了研究,采用了先整体后局部的分析方法,即在风-汽车-桥梁耦合分析时先不考虑驾驶员行为和汽车侧偏,将分析得到的汽车竖向和滚动等自由度方向的振动加速度时程作为激励,对考虑侧向自由度和驾驶员行为的汽车模型作独立的分析。本文在以往风-汽车-桥梁耦合振动分析程序[7]的基础上,增加汽车的侧向自由度,将驾驶员行为数学模型嵌入到整体的风-汽车-桥分析系统中,使风-汽车-桥系统能够直接分析振动桥面上汽车的车轮侧偏、支撑力响应,为分析桥面行车安全及临界风速提供分析工具。并以此研究和比较桥面典型车辆的临界风速。
1 考虑驾驶员行为的风-汽车-桥梁耦合振动
车辆和桥梁之间的耦合关系使得车-桥系统成为相互影响的耦合系统,侧风对桥梁结构和行驶汽车的作用,及结构振动对流场的影响又使得风-汽车-桥梁成为一个大的系统。
1.1 两轴车辆的动力学模型和运动方程
在研究车和桥梁的相互作用时,汽车被模型化为弹簧、阻尼装置相连的几个刚体和质量块[5,6]。对于两轴四轮车辆,整个车辆可以分成5个刚体部件:1个车体、4个车轮,刚体之间通过弹性元件和阻尼元件相互连接。车体具有五个自由度:横移、浮沉、侧滚、点头及摇头。每个车轮具有2个独立的自由度:横移和竖移。为了研究车辆突然受到侧风引起的驾驶方向偏离,车辆轮胎与地面之间的侧向位移作为独立自由度。车辆的总的独立自由度个数为17,表示如下:
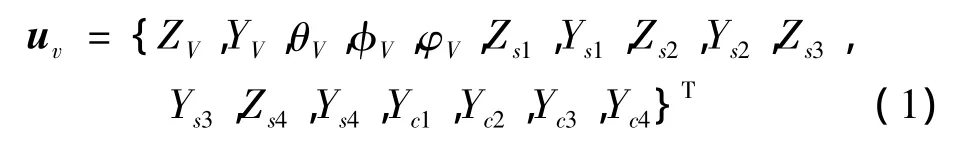
其中 ZV,YV,θV,φV,φV分别表示车体的浮沉振动、横摆振动、点头振动(绕Y轴)、侧滚振动(绕X轴)、摇头振动(绕 Z 轴);Zsi,Ysi(i=1,2,3,4)表示四个车轮浮沉振动、横摆振动;Yci表示车轮与路面接触点侧向相对滑动。
车辆子系统车体部分和车轮的运动方程[4]在此不再赘述。要分析车辆在桥上的侧偏,这里需要特别关注车轮与路面接触点的运动方程。轮胎在Y方向运动平衡方程为:
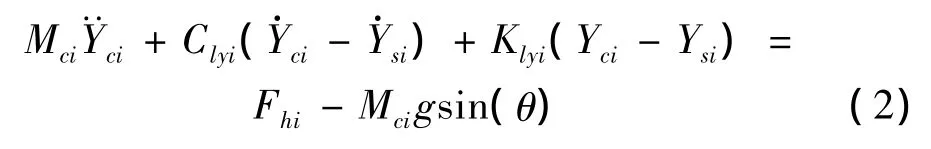
其中Fhi(i=1,2,…,4)为第i个轮胎与路面的侧向接触力,即轮胎侧滑力。根据轮胎的侧偏方程,侧滑力一般可以线性地表示为:
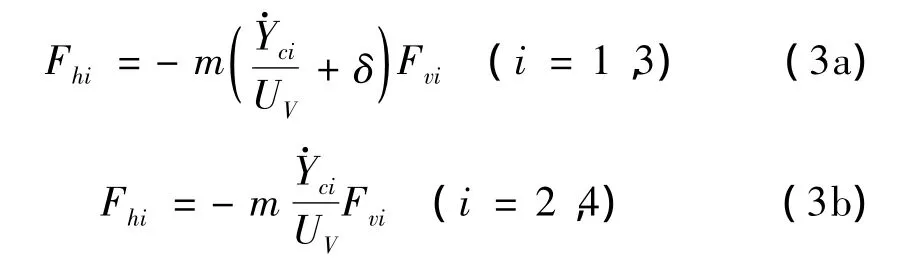
其中m为侧滑摩擦系数;负号表示侧滑力始终抵抗轮胎相对于路面的侧向运动;Fvi为第i个轮胎与路面的竖向接触力。δ是前轮转向角,由驾驶员行为调整。将式(3)代入式(2)可得:

综合车体、车轮运动方程及车轮与路面接触点的运动方程,可以得到车辆运动方程的矩阵形式,具体表达式见文献[8] 。
1.2 侧风作用下的驾驶员行为模型
汽车在侧向风作用下,驾驶员不断调整转向盘以保持车辆平衡。Baker曾经提出一个适用于风环境下的转向角模型,这个模型与汽车的侧向干扰运动和侧向速度有关。Cai、Chen[5]提出了一个与 Baker模型相类似的驾驶员行为模型。但Chen认为驾驶员行为模型不应仅以车体重心处的侧向位移为控制目标,还应控制汽车的偏航角,因此以前轮的侧向滑动为控制目标更加合理。模型的数学表达式为:
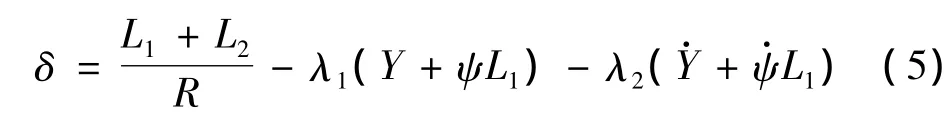
其中δ为驾驶员控制的前轮转向角,R为旋转半径,L1和L2分别是车辆质心处到前轮和后轮的距离,λ1和λ2为与驾驶员行为有关的参数,Y和为车辆质心的侧向位移和侧向速率,ψ和为车体部分的偏航角和偏航角速率。
跨海大桥桥面高、风速大,在侧风作用下车辆将发生较大的偏航角,由于车轮的侧滑力总是垂直于车轮所在平面,而车轮是随车体偏航角转动的,汽车运动方程所处坐标系也是随着偏航角转动的,所以由汽车运动方程解析出来的侧滑位移是垂直汽车车身方向的。显然,驾驶员行为调整的是车辆对于车道的侧偏,驾驶员行为模型中的侧滑位移和速率应该是垂直车道方向的。为此,日本学者Yoshimoto[9]曾提出了驾驶员行为的二阶预测修正模型,该模型的合理性正在于它考虑了偏航角对运动方程坐标系的影响。
本文拟采用与式(5)形式相似的驾驶员行为模型,但其中的侧滑位移和速率项将考虑偏航角的影响。此外,在侧风作用下,桥面也会发生侧向振动,所以,在计算汽车相对桥面的侧偏时,还应该考虑桥面的侧摆。经分析,汽车重心与桥面相对滑移速度在垂直车道中心线方向的投影为:
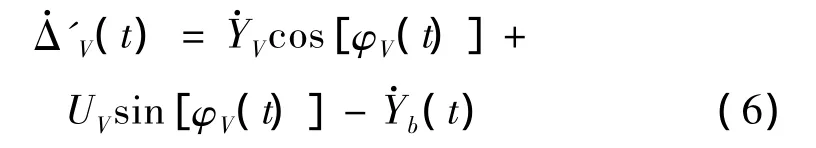
其中第一项为车体侧滑速度在垂直车道方向的投影,第二项为车速的投影,第三项为桥面振动的侧向速率。φv为汽车的偏航角为车辆刚体部分重心的侧向速率为车辆重心处桥面的侧向速率。对式(6)进行积分,得到汽车与桥面的侧向相对位移在垂直桥面方向的投影为:

其中Yb为车辆重心处桥面的侧向位移。有了相对位移和速度的投影以后,可以将式(5)的驾驶员行为模型修正为:
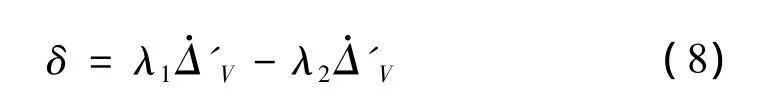
其中λ1和λ2可参考文献[5] 的取值。
式(8)用汽车重心的侧滑计算转向角,即驾驶员行为以控制重心侧滑为目标。当驾驶员行为模型以控制前轮侧滑为目标时,只要将式(6)~式(8)中的置换为前轮的侧滑和速率即可。另外,驾驶员调整方向盘的频率也是驾驶员行为特征的重要方面。驾驶员长时间高频率地转向是不现实的。当风速小于15 m/s时,转角调整频率采用1 Hz;风速大于15 m/s时,频率采用 2 Hz[5]。
1.3 考虑驾驶员行为的风-汽车-桥梁耦合振动
风荷载作用下,桥梁结构动力学方程为:

其中KbT表示桥梁的切线刚度矩阵,它包括弹性刚度矩阵、初应力刚度矩阵及大位移刚度矩阵;阻尼矩阵Cb用正交瑞利形式。Fb(t)表示桥梁结构上外荷载产生的等效节点力:

其中 Fbg、Fstb、Fbub、Fseb分别表示自重、静风力、抖振力、自激力产生的节点力。
综合侧风作用下的汽车子系统运动方程、桥梁子系统的运动方程,以及车辆和桥梁竖向的几何和力学耦合关系[9],联立式(8)所示的驾驶员模型,得到完整的考虑驾驶员行为的风-汽车-桥梁耦合分析系统。在系统的求解策略上,采用分离迭代法:即分别求解车辆与桥梁的运动方程,以车与桥的位移协调为收敛条件。相应的分析程序是在文献[7] 的基础上进一步完善的。
1.4 车辆的事故标准
Baker等曾经对交通事故认定提出一些指导方针:当其中一个轮胎的支反力为零时,认为发生侧倾事故;车辆的侧滑响应超过0.5 m时认为发生侧滑事故;偏航角超过0.2 rad时发生打转事故。理论上,只有当车辆重心抬高到一定高度才可能导致翻车,有经验的驾驶员在一个车轮已经离开地面后能够稳住汽车,汽车越过车道也只是潜在的不安全因素,然而设定较为保守的事故评价标准对普通驾驶员有重要意义。
随着风-汽车-桥梁耦合振动研究的逐步精细化,车辆动力学模型已经能比较好地仿真,可以详细计算出车辆重心、前轮、后轮的侧向位移及偏航角,因而,可以直接用前轮、后轮侧滑响应来判断汽车是否越过车道。在高速公路上,车宽一般不超过2.5 m,标准的车道宽是3.75 m,又侧风作用下汽车前、后轴的垂直车道线方向位移相反,拟设置侧滑临界值为0.5 m。这样的设置对于小汽车来说是偏安全的。于是,将侧滑事故和打转事故都归属为侧滑事故。与侧滑事故相关的侧滑位移称为侧滑事故相关响应,侧倾事故相关的支撑力称为侧倾事故相关响应。
2 数值算例
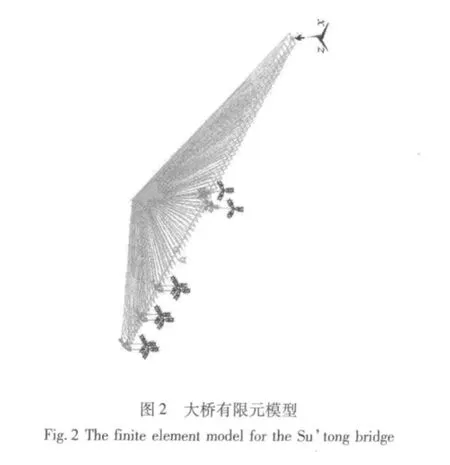
以苏通大桥为工程背景。苏通大桥是一座现代化桥梁,是目前世界上最大跨度的斜拉桥。大桥采用倒Y型桥塔、斜索面和闭口钢箱梁主梁断面,其跨径组成100.00+100.00+300.00+1088.00+300.00+100.00+100.00 m,主梁高 4.00 m,宽 41.00 m,倒 Y型桥塔高300.40 m。大桥主梁断面见图1,图2为大桥的有限元模型,大桥是对称结构,这里给出了一半结构的模型。大桥的气动力系数采用文献[10] 中高雷诺下的结果。

2.1 系统激励的随机模拟
风-汽车-桥梁系统的激励为脉动风和桥面粗糙度。现场的风观测只能得到少数几个观测点的风谱参数及相关性。在桥梁风工程中,大桥的风场需要采用随机模拟的方法得到。桥面的粗糙度也可采用谐波合成法模拟得到。目前谐波合成法是模拟大桥风场最常用的方法,但由于大跨桥梁的跨度很大,风场的空间相关性导致风场模拟的计算量很大。快速傅里叶变换技术(FFT)及用拉格朗日插值减少风谱矩阵的分解次数都可以大大增强谐波合成法的计算效率[11]。图3给出了插值法改进后的谐波合成法得到的苏通大桥平均风速为10 m/s、20 m/s、30 m/s时主梁跨中的横桥向脉动风速时程。路面粗糙度取好的情况时(粗糙度系数Ar取20×10-5m3/cycle),模拟得到的样本及其导数如图4所示。限于篇幅,其它的结果不再列出。
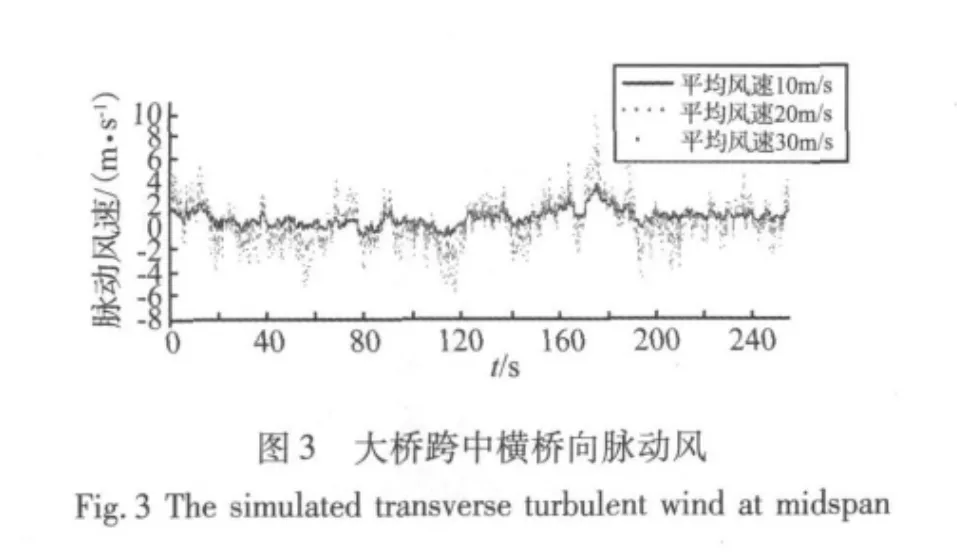
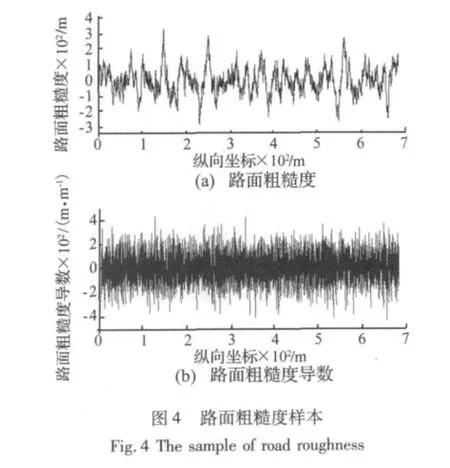
要求解大桥桥面的行车临界风速,需要计算不同风速和车速下系统的响应,但即便是用改进以后的方法模拟大桥的风场仍要耗费大量的机时,所以在求解临界风速时,在每个平均风速下都重新模拟风场是不现实的。本文在模拟10 m/s、20 m/s、30 m/s三个平均风速下的风场时采用了同一个随机相位角序列,所以图4中三个脉动风时程有完全一致的相位角,且经计算,20 m/s下的脉动风与10 m/s和30 m/s下脉动风的平均值相差很小。这些特点使得平均风速在10 m/s~30 m/s时,脉动风场能够通过对平均风速进行插值运算得到。
2.2 行车事故相关响应特征
Baker采用的驾驶员行为模型是控制车辆重心位移,Chen倾向于采用控制前轮位移的驾驶员模型。根据常识经验,实际的驾驶员行为介于两者之间。此处最关心的是驾驶员行为模型的不同控制目标是否会显著影响临界风速的计算结果。为此,以箱式货车为分析对象,研究侧风环境下汽车在桥面行使时事故相关响应的特征,并对控制车体重心侧滑时的车辆响应和控制前轮的进行比较。该箱式货车尺寸参数、力学参数和气动参数参照文献[6] 的实验结果。驾驶员模型中的参数采用 λ1=0.3、λ2=0.2[5]。车速采用 60 km/h,风速为20 m/s(10 m高风速,换算到桥面高程为27.05 m/s)。得到的行车事故相关响应如图5-图8所示。
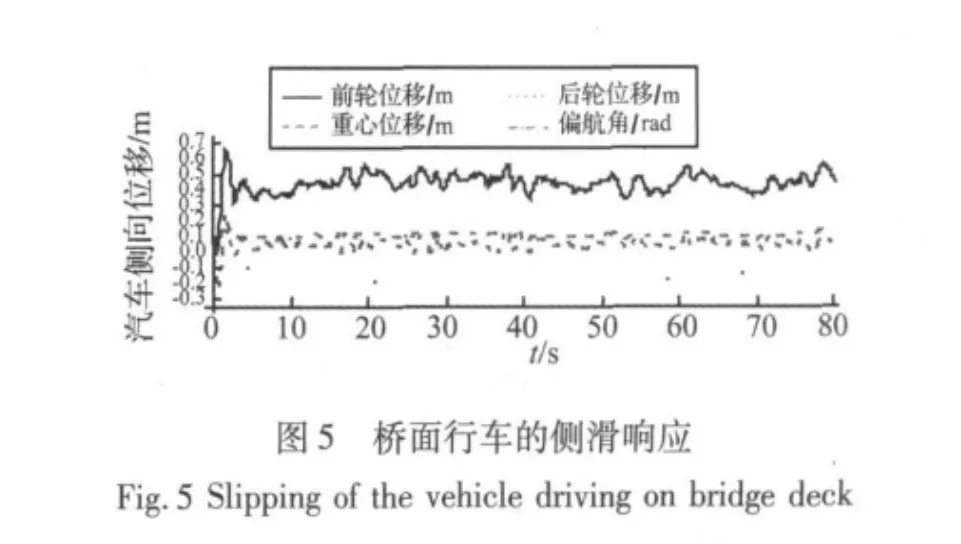


图5、图6给出了驾驶员行为控制车体重心侧偏时桥面行使车辆的侧滑响应和支撑力响应,图7、图8给出了驾驶员模型控制前轮侧偏时的情况。比较可见,控制重心侧偏或前轮侧偏时,得到的侧倾事故相关响应没有明显差别,但侧滑响应有很大不同。
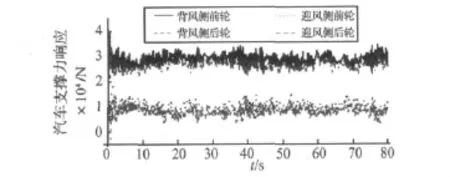
图8 桥面行车的车轮支撑力响应Fig.8 Contact force of the vehicle driving on bridge deck
从图5可见,在侧风作用下桥面汽车的侧滑响应在不足2 s时间内完成突变,之后围绕平均值脉动。前轮朝气流的上游偏移,后轮朝下游偏移,汽车重心位移也不是在车道中线摆动,而是朝气流上游方向有小的偏移。偏航角不是在零附近波动,即侧风作用下汽车总以保持一定偏航角的姿态行使。这说明驾驶员行为可以控制车辆侧偏,但不能消除车辆的偏航角,这是由于在侧风作用下汽车气动力的合力作用线并不通过汽车重心。
从图6和图8可见,迎风侧支撑力的比背风侧的小很多,说明侧风为20 m/s时对汽车已经有比较大的影响。汽车前轮的支撑力比后轮要大,是由于汽车的重心靠近前轴,前轮分担的重力大于后轮。只有当车速非常高时,气仰力矩才会使前轮支撑力小于后轮。
比较图5和图7可见,采用控制重心的驾驶员模型时,前轮侧滑位移较后轮大,前轮最大值约0.65 m,后轮最大值不足0.3 m。采用控制前轮位移的驾驶员模型时,前轮的位移最大值约0.3 m,但后轮位移最大值达0.65 m。可见,尽管采用两种不同的驾驶员模型会得到完全不同的侧滑响应,但侧滑位移最大值却相差不大。因此,采用这两种驾驶员模型得到的临界风速差别不大,即驾驶员行为控制对象的不同不会显著影响临界风速。后面的分析将采用控制重心侧偏的驾驶员模型。
2.3 典型车辆的桥面行使临界风速
求解临界风速步骤如下:选定车速和路面粗糙度样本,初步拟定平均风,通过平均风插值运算得到脉动风场,用耦合分析程序得到汽车的事故相关响应,逐级增加平均风,直到出现侧滑或侧倾事故的临界状态,即得到相应的临界风速。以此方法可以得到不同车速和路面粗糙度情况下的临界风速。

图9 箱式货车的临界风速Fig.9 Critical wind velocity for box-type truck
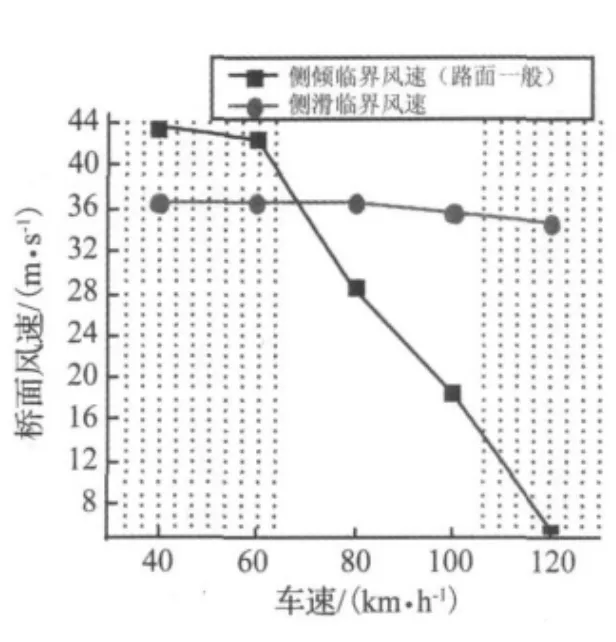
图10 桑塔纳的临界风速Fig.10 Critical wind velocity for Santana
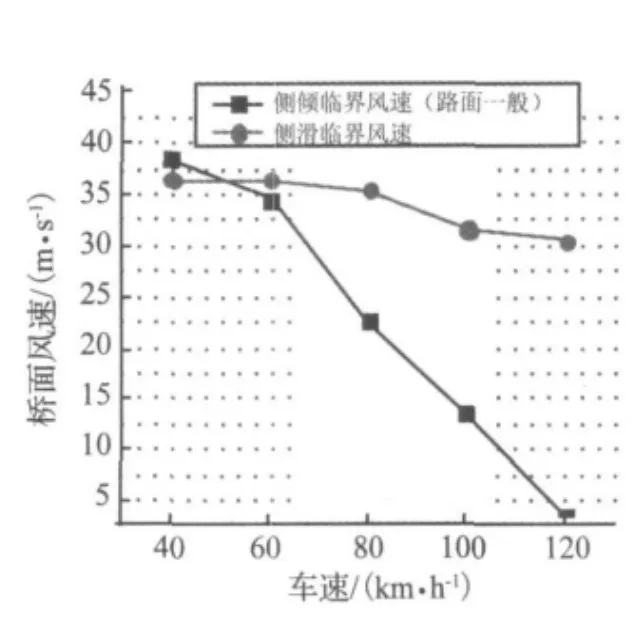
图11 一汽佳宝的临界风速Fig.11 Critical wind velocity for Jia-ba
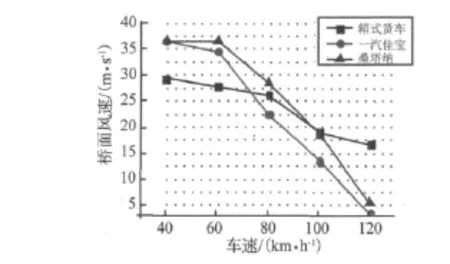
图12 典型汽车临界风速比较Fig.12 Comparison of critical wind velocity for three kind of typical vehicles
图9~图11分别给出了苏通大桥桥面上箱式货车、桑塔纳和一汽佳宝的侧倾、侧滑临界风速。图9显示,对于箱式货车,侧滑临界风速低于侧倾临界风速,侧滑事故起控制作用。这是因为箱式货车的车身长、车体重。对于桑塔纳和一汽佳宝,图10、图11显示,车速低时,侧滑事故起控制作用;车速度高于50 km/h或70 km/h后,则侧倾事故起控制作用,即在强侧风环境下小汽车高速行驶引起的交通事故是最严重的翻车。因为分析模型假定车辆和桥梁接触,所以比侧倾临界风速大的侧滑临界风速实际上已经没有意义。图12比较了三种典型车辆的桥面行驶临界风速(取侧倾和侧滑临界风速中较小的)。从中可见,低车速时,大车的临界风速比小汽车的要低;高车速时,小汽车的临界风速比大车低,说明强侧风下小汽车更不易高速行驶。图12还显示,一汽佳宝的临界风速略低于桑塔纳,说明还在强侧风环境下佳宝汽车的行驶稳定性还略逊于桑塔纳。
3 结论
本文深入分析了汽车运动方程的随动坐标特性和桥梁抖振对汽车相对桥面侧偏的影响,在以往风-汽车-桥系统研究的基础上,考虑了汽车在桥面的侧偏和驾驶员行为的作用,实现了相应的程序模块。以某斜拉桥为背景,分析了三种典型车辆在桥面行驶时的临界风速,得到了如下结论:
(1)汽车运动方程的坐标系是随着汽车的偏航角而转动的,因此由运动方程得到的侧滑位移不是驾驶员行为要直接控制的对象。应以车轮与桥面接触点的相对速度和位移在垂直车道方向的投影为控制目标,并考虑桥的侧向振动的影响,得到适合强侧风环境的驾驶员行为数学模型。
(2)不同类型车辆的事故类型不同。对于箱式货车,侧滑事故起控制作用;对于桑塔纳和一汽佳宝,车速低时侧滑事故起控制作用,车速度高于50km/h或70km/h后,侧倾事故起控制作用。
(3)低车速时,货车的临界风速比小车低,因为货车更容易越过车道;高车速时,小汽车的临界车速比货车低,说明在有强侧风作用时小汽车更不易高速行驶。一汽佳宝的临界风速略低于桑塔纳。
桥面行车安全的研究涉及很多方面的内容,如汽车经过桥塔时,其周围流场发生剧烈变化,其气动力的测试需要专门的风洞试验支撑,驾驶员行为数学模型的参数测定也需要专门的研究。本文对风-汽车-桥梁分析体系的完善是重要的方面,所得结论具有参考价值。
[1] 夏 禾,徐幼麟,阎全胜.大跨度悬索桥在风与列车荷载同时作用下的动力响应分析[J] .铁道学报,2002,24(4):83-91.
[2] 李永乐.风-车-桥系统非线性空间耦合振动研究[D] .成都:西南交通大学,2003.
[3] 李雪冰,侯传伦,张曙光,等.高速列车交会时的风致振动研究[J] .振动与冲击,2009,28(7):81 -84,94.
[4] Guo W H.Dynamic analysis of coupled road vehicle and longspan cable-stayed bridge systems under cross winds[D] .Department of Civil and Structrual Engineering of the Hong Kong Ploytechnic University,2003.
[5] Chen S R.Dynamics performance of Bridges and vehicles under strong wind[D] .Louisiana State University and Agriculture and Mechanical College,2005.
[6] 韩万水.风-汽车-桥梁系统空间耦合振动研究[D] .上海:同济大学,2006.
[7] 周 立.大跨度桥梁风振和车辆振动响应及其疲劳性能研究[D] .上海:同济大学,2008.
[8] 马 麟.考虑驾驶员行为的风-汽车-桥梁系统空间耦合振动研究[D] .西安:长安大学,2008.
[9] Yoshihisa K.Simulation of driver-vehicle systems using a predicable model of driver’s steering[J] .Journal of Japanese Society Mechanics Engineering.1968,596(71):93 -107.
[10] 刘健新,崔 欣,李加武.桥梁断面表面压力分布及Strouhal数的雷诺数效应[J] .振动与冲击,2010,29(4):146-149.
[11] 丁泉顺,陈艾荣,项海帆.大跨度桥梁空间脉动风场的计算机模拟[J] .力学季刊,2006,27(2):184 -189.
