非线性振动方程多重解求解方法

钱征文，程 礼，陈 卫，李应红

(空军工程大学 工程学院，西安 710038)

非线性振动分析中一个重要方面是研究系统的周期解及其稳定性。一般说来，借助于数值方法可获得系统的稳定周期解，但由于其解曲线敏感依赖于初值的选择，将很难获得多解及其不稳定解，因而需要借助于各种近似方法。

对于简单的具有多重解的振动方程，如Duffing振子，许多作者［1－7]已利用谐波平衡法分析了其稳定响应，即假定振动响应可被表示成简单的截断傅里叶级数，从而将Duffing振子方程化为一个非线性代数方程组。但对于一些复杂的具有多重解的振动方程，其对应的非线性代数方程组非常复杂，可能依赖于不同的初值存在多重解，并且不稳定解支的收敛域往往都很小，很难去直接求解。常用的求解非线性代数方程组的方法，如:牛顿迭代法、梯度下降法、拟牛顿法等对初值的选取是敏感依赖的，在求解多解问题时效果不能令人满意。此外，当追踪参数变化下系统的振动响应时，传统的方法是在给定的初值下重复迭代求解过程，效率较低，初值选取不当不仅浪费很多计算时间，甚至有可能造成求解失败。

针对上述问题，考虑到同伦算法可以扩大迭代格式的收敛域，将其引入到方程的求解中。同时为避免重复迭代求解效率低的问题，采用预测校正算法来追踪解曲线，从而确定非线性方程的稳定周期解和不稳定周期解。

1 求解方法推导

对于非线性振动方程，一般表示为:

由谐波平衡法可以得到关于n个谐波系数以及外激励频率ω的非线性方程组:

式中，u=(a1，a2，…，an)，ai为第 i个谐波系数，n 的取值与选取的近似解的阶数有关。

1.1 预测校正算法［8]

将非线性方程组(2)的解曲线问题转化为常微分方程的柯西问题:

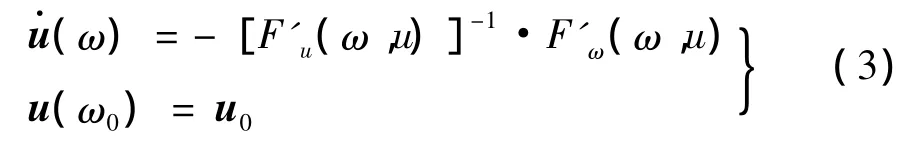
这样，采用欧拉法或者其他更高阶数值方法求得一条通过(u0，ω0)的积分曲线就是方程组(2)的解曲线，得到了谐波系数就可以确定非线性振动方程(1)的近似解。

采用欧拉型积分公式，则有:

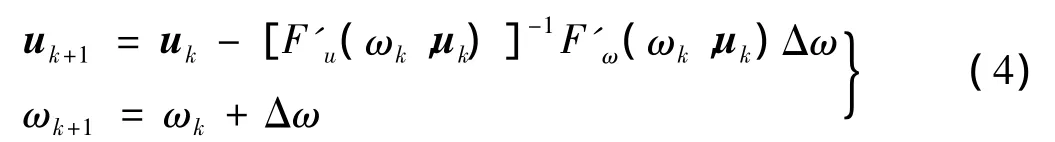
在式(3)的一步步求解过程中，可以不时地利用式(2)进行一般牛顿迭代的修正:

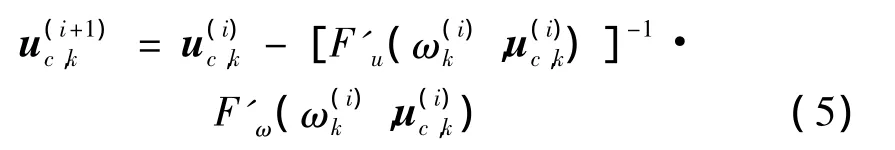
使近似解点充分逼近解曲线，误差满足精度要求。

上述算法的具体实施过程中，对于有多重解存在的情况，步长Δω的选取十分重要，较大的步长会造成解突然从一个解支跳到另一个解支。为避免这种情况发生，在保证计算效率的同时可以尽量选取较小的步长。

1.2 同伦算法

利用预测校正法求解非线性方程组(2)的过程中，需要确定初始值(u0，ω0)，通常情况下初始值的选取取决于计算者的经验，并无特殊考虑，因此，初始值选取是方程求解的关键。而当非线性方程组存在多解的情况时，初始值的选择就更为困难。

同伦算法［9]是一种有效的方法，在扩大迭代格式收敛域方面起着关键作用，理论上对迭代初始值的选取没有任何限制。将同伦算法引入非线性方程组的求解中，就可以利用其全局搜索能力来提高解的收敛性。

为求非线性方程F(u，ω)=0的解，构造一个带有参数 t的映射 H∶［0，1] × Rn→Rn，使得:

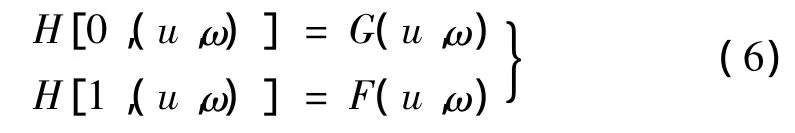
其中，方程 G(u，ω)=0的解已知，这个映射H［t，(u，ω)] 就称为同伦映射。

通过同伦映射，把求解方程F(u，ω)=0转化为求解同伦方程H(t，(u，ω))的解。如果同伦方程对任何0≤t≤1有解u(t)存在，那么对应于Rn中的解曲线u(t)，起点为u(0)，终点为u(1)，且有:

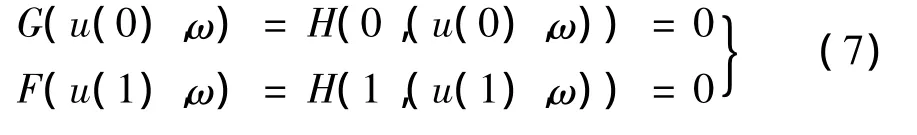
由式(7)可以看出，终点u(1)就是所求的方程F(u，ω)=0的解。

由于方程G(u，ω)=0的解是已知的，也就是解的初始点已知，追踪解曲线的过程可以运用前面的预测校正算法，从初始点起追踪曲线u(t)直到终点u(1)，就可以得到原方程F(u，ω)=0的解。

常见的同伦映射有以下三种形式:

(1)不动点同伦映射:H(t，x)=tF(x)+(1－t)·［x－x(0)] ;

(2)牛顿同伦映射:H(t，x)=F(x)－(1－t)F·［x(0)] ;

(3)线性同伦映射:H(t，x)=tF(x)+(1－t)·G(x)。

本文采用牛顿同伦映射算法。

1.3 计算步骤

将同伦算法与预测校正算法相结合，求解外激励参数变化下非线性振动方程(1)周期解的步骤如下:

① 对方程(1)用谐波平衡法得到关于n个谐波系数以及外激励频率ω的非线性方程组F(u，ω)=0;

② 构造同伦映射，方程G(u)=0的解即是迭代初始值;

③ 在ω=ω0下，借助预测校正算法，利用式(4)和式(5)，以t作为外激励参数，追踪解曲线u(t)，终点u(1)就是所要求的方程F(u，ω0)=0的解;

④ ω=ω0+Δω，以u(t)为迭代初始值，以ω作为外激励参数，借助预测校正算法，得到方程组F(u，ω)=0的解;

⑤ 改变ω，重复上一步，得到每一个ω下方程组F(u，ω)=0的解 u(ω);

⑥ 将u(ω)的带入相应的谐波系数得到方程(1)的周期解。

对于有多解存在的情况，在构造同伦映射时，可以通过改变方程G(u)=0使迭代初始值在大范围内变化，从而搜索得到不同的解。

2 计算验证

一般地，工程结构中梁的非线性振动问题以及许多电路模型均可表示为非线性Duffing振子的形式，其振动方程为:

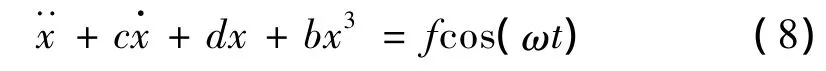
式中，c为阻尼系数，d为线性刚度系数，b为非线性刚度系数，f为外激励载荷，ω为外激励频率。

取方程(1)的一阶近似解为x=A cos(ωt+φ)，则其理论解［10]为:

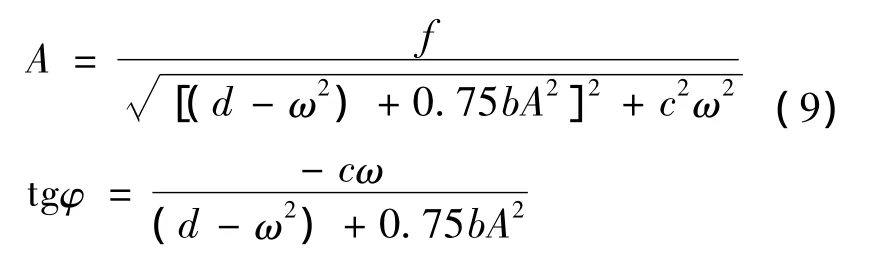
取系统参数如下:c=0.28，d=1，b=2.5，f=0.82。由式(9)可得非线性Duffing振子(式(8))的幅频曲线如图1所示。

运用本文的算法对方程(8)进行求解，假设其一阶近似解为 x=A1cos(ωt)+A2sin(ωt)，幅值利用谐波平衡法可得:

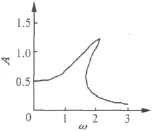
图1 非线性Duffing振子的理论解幅频曲线Fig.1 Amplitude-frequency curve of nonlinear Duffing oscillator

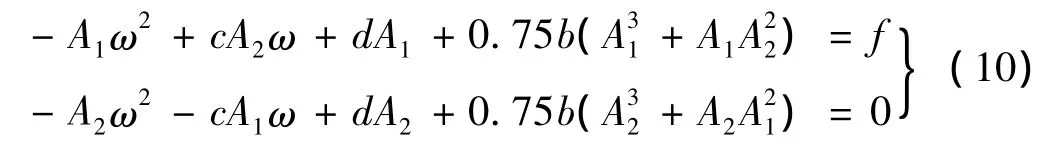
通过初值搜索可以得到非线性Duffing振子的三个解支，如图2所示。

三个解支中，虚线所表示的解支是不稳定的周期解，两外两个解支则为稳定的周期解。从图中可以看到，采用本文的方法计算得到的结果与理论近似解(图1)是吻合的。

将四阶龙格－库塔法求得的周期解与使用本文方法求解的结果进行对比，如图3所示。系统参数取值为:c=0.28，d=1，b=2.5，f=0.82，ω =2.0。

从图中可以看出，对于幅值较小的周期解，两种方法的结果非常接近［图3(a)] ;对于幅值较大的周期解，两种方法的结果有一定的差距［图3(b)] ，这主要是因为一阶近似解中忽略了高阶信号，存在阶段误差。实际上，使用本文方法求解时，近似解中考虑的阶数越高，两者的误差就会越小。图3(c)是用本文方法求得的不稳定周期解的相图，而龙格－库塔法无法求得不稳定周期解，只能得到稳定的周期解。

3 算例

拉杆转子是各类航空发动机及大型燃气轮机中常用的一种转子结构形式，由于盘与盘之间靠拉杆螺栓连接，并不是一个连续的整体，其转子振动特性非常复杂。本文通过合理地简化，构建转子的运动方程，利用上述方法对其振动特性进行研究。简化后转子的力学模型如图4所示。

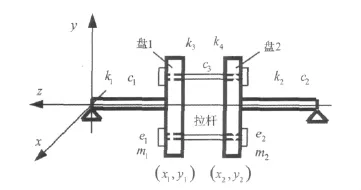
图4 简化后转子力学模型Fig.4 Sketch of simplified mechanical model

盘简化为质量分别是m1、m2的两个刚性圆盘，偏心量分别为e1、e2，两盘质量偏心矢量夹角为φ。拉杆结构简化为等效的抗弯弹簧，不计弹簧的质量，具有非线性的刚度特征，其弹性回复力可表示为p(x)=k3x+。两端分别与不计质量的弹性轴相连，轴的弯曲刚度分别为k1、k2。轴、抗弯弹簧的阻尼系数分别为c1、c2、c3。

只考虑该转子模型在x－y平面内的弯曲振动，忽略圆盘重力的作用，则圆盘的质心运动方程可表示为:

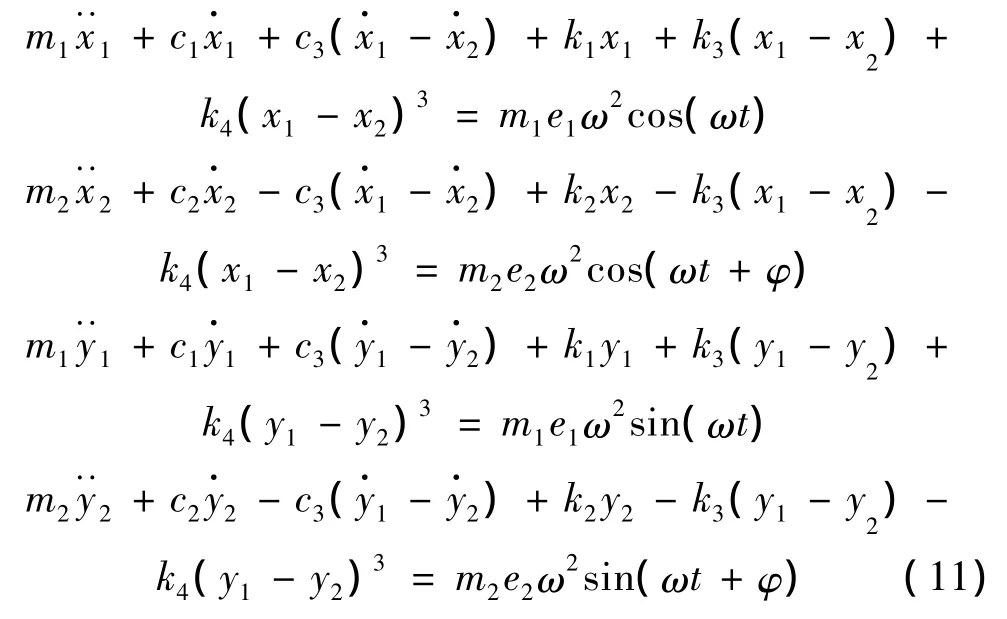
由于转子在x和y方向的刚度、阻尼相同，不考虑重力作用时两个方向的振动相同，本文只考虑x方向的振动。

设方程(11)的稳态近似解为:x1=A1sin(ωt)+A2cos(ωt)，x2=A3sin(ωt)+A4cos(ωt)，y1=A5sin(ωt)+A6cos(ωt)，y2=A7sin(ωt)+A8cos(ωt)。

其中，A1、A2、A3、A4、A5、A6、A7、A8为待定系数。将近似解代入方程(11)中，平衡正弦和余弦函数系数后可得:

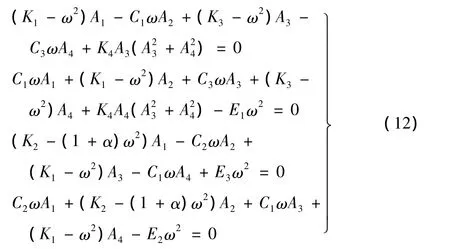
其中:

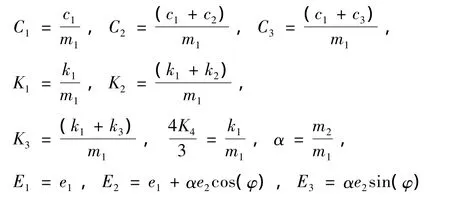
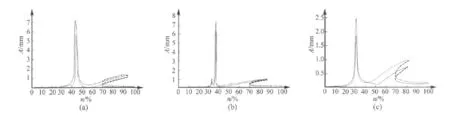
图5 不同参数下的振幅随转速变化曲线Fig.5 Vibration curve with different parameters

分别取不同的系统参数，对拉杆转子的双稳态特性进行仿真计算和分析，计算中，参数取值如下:

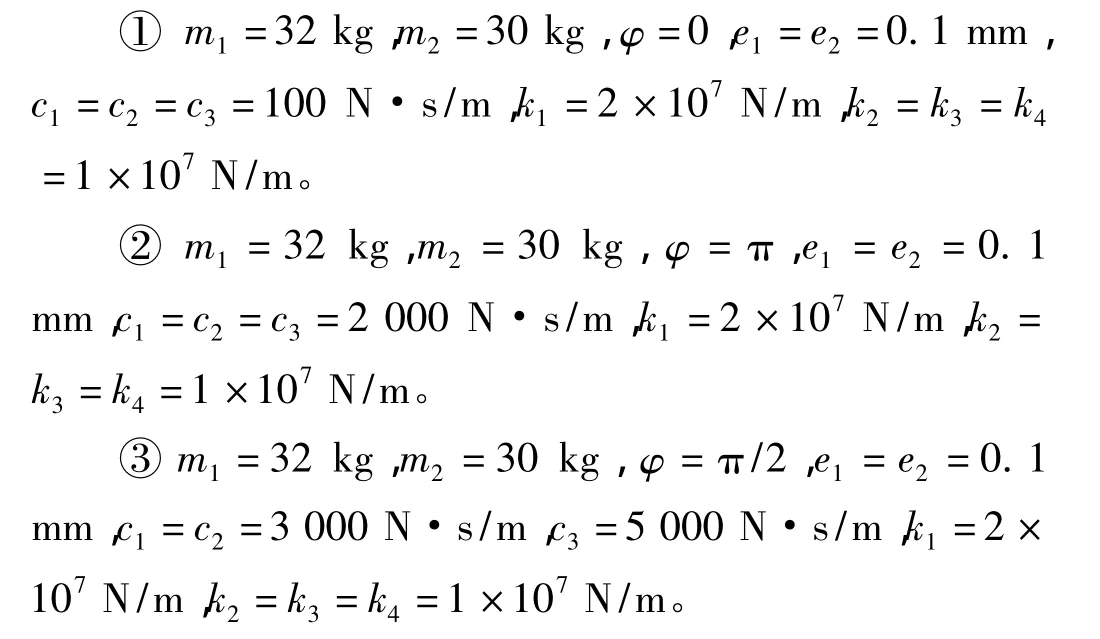
图5是转子x方向振动幅值随转子转速变化的曲线图。红线和蓝线分别是盘1和盘2质心的振幅曲线，横坐标表示的是相对转速，100%时转速为2 000 rad/s。

通过计算可知，不稳定解的收敛域很小，常用的求解微分方程的方法无法得到不稳定解。利用本文提出的求解方法，可以快速地求出两个稳态解(图5中实线所示);对于不稳定的解(图5中虚线所示)，通过同伦算法扩大收敛域后，可以准确追踪不稳定的解曲线。仿真计算验证了该方法的有效性。

4 结论

本文提出的方法可以解决迭代初值难以确定的问题，有效地求解非线性振动方程的多重解。由于迭代初值的选取没有限制，通过全局搜索，不但可以计算稳定的周期解，而且不稳定的周期解也可以求出。通过使用预测－校正算法，可以快速求解外激励参数变化下的周期解。此外，由于该方法减少了迭代求解的计算量，在使用谐波平衡法时，可以选取任意阶数的谐波，因此该方法可以求解任意精度的周期解。本文的研究成果可进一步推广于求解其他类型的非线性方程。

［1] Ickens R E M.Comments on the method of harmonic balance［J] .Journal of Sound and Vibration，1984，94:456 －460.

［2] Hamdan M N，Burton T D.On the steady state response and stability of non-linear oscillators using harmonic balance［J] .Journal of Sound and Vibration，1993，166(2):255 －266.

［3] 李鹏松，吴柏生.达芬－谐波振子的改进解析逼近解［J] .振动与冲击，2004，23(3):113 － 116.

［4] 李银山，张善元，董青田，等.用两项谐波法求解强非线性Duffing方程［J] .太原理工大学学报，2005，36(6):690－693.

［5] 胡 辉，郭源君，郑敏毅.一个非线性奇异振子的谐波平衡解［J] .振动与冲击，2009，28(2):121 － 123.

［6] 高 阳，王三民，刘晓宁.一种改进的增量谐波平衡法及其在非线性振动中的应用［J] .机械科学与技术，2005，24(6):663－665.

［7] 杨绍普，申永军，刘献栋.基于增量谐波平衡法的齿轮系统非线性动力学［J] .振动与冲击，2005，23(4):40 －42.

［8] 虞 烈，刘 恒.轴承－转子系统动力学［M] .西安:西安交通大学出版社，2000.

［9] 何哲明，李 赞.同伦算法的常微分方程数值解法及在机构学中的应用［J] .机床与液压，2003，1:214 －216.

［10] 郝亦清，李翠英.非线性振动分析［M] .北京:北京理工大学出版社，1996.