基于自适应蚁群优化的Volterra核辨识算法研究

李志农，唐高松，肖尧先，邬冠华

(1.南昌航空大学 无损检测技术教育部重点实验室，南昌 330063;2.郑州大学 机械工程学院，郑州 450001)

蚁群优化(Ant Colony Optimization，ACO)算法是20世纪90年代意大利学者Dorigo［1]提出的一种新型模拟进化算法。它具有较强的鲁棒性、良好的搜索性能和并行运算能力。其研究已经渗透到许多应用领域，为多维动态优化问题提供了一种新的智能方法。基于Volterra级数模型的非线性系统辨识已经成为当前非线性研究领域的一个热点，该模型的辨识实质上是一个优化问题，基于此，我们把蚁群优化引入到非线性Volterra级数模型辨识中，提出了一种基于蚁群优化的Volterra核辨识方法［2]，该方法与传统的基于最小二乘算法的Volterra级数模型辨识方法相比，它克服了传统方法要求目标函数连续可导，对测量噪声很敏感，且需要利用梯度信息等缺陷。

然而，随着研究不断深入，我们发现，基于蚁群优化的Volterra级数模型的非线性系统辨识方法存在一些不足，如在算法，蚁群中多个个体的运动是随机的，当群体规模较大时，要找出一条较好的路径需要较长的搜索时间，另外，在算法中采用了正反馈机理，正反馈过强，很容易使优化过程陷于局部极小，正反馈强度过小，则使运行速度过慢，要得到最优解，往往需要很长的寻优时间。

针对基于蚁群优化的Volterra级数模型的非线性系统辨识方法存在的以上不足，本文将自适应的蚁群算法引入到非线性系统的Volterra时域核辨识中，提出了一种基于自适应蚁群优化的Volterra核辨识算法。通过自适应地改变记忆因子、挥发因子以及状态转移概率，使得本算法在搜索前期具有较大的随机性，提高全局搜索能力，在搜索后期，降低随机性，使算法能快速收敛。仿真结果表明，与传统蚁群优化Volterra核辨识算法对比，本文提出的算法的收敛速度与鲁棒抗噪性能有了明显提高，并具有同样好的收敛精度。

1 非线性系统Volterra级数模型的建立

Volterra级数模型已成为研究非线性系统的强有力的模型之一，它是线性系统脉冲响应函数模型对非线性系统的直接扩展，能够描述一大类非线性系统。非线性系统的Volterra时域、频域核属于非参数模型，它不依赖于系统的输入，因而完全反映了系统的本质特性。

设非线性系统可用记忆长度为M的N阶Volterra级数模型近似描述，其离散截断形式的Volterra级数模型可以描述为［3，4]:

其中，hn(m1，…，mn)称为非线性系统的 n阶 Volterra时域核，又称为广义脉冲响应函数。hn(m1，…，mn)具有对称性，且对称性是唯一的，利用Volterra核的对称性，可大大减小用Volterra级数模型描述非线性系统所需的参数数目，从而可大大减小计算量。

式(1)可以写成以下形式:

式中，Y为输出观测向量，U为输入矩阵，H为非线性系统Volterra核向量。Y，U，H的表达式如下;

由式(2)可知，Volterra核向量的辨识实质是一个最优参数估计问题，利用系统的输入输出数据可以辨识Volterra核向量。在此，我们采用自适应蚁群优化算法来求解Volterra核向量。

2 自适应蚁群优化算法

普通蚁群算法是通过增加行经路径上的信息素的办法来强化较好的解。搜索开始时，信息素的分布是分散的，在算法进化一定的迭代步数后，信息素会集中到少数边上，搜索方向也随之基本上确定下来。当某些边上的信息素强度明显高于其余边时，导致在搜索时，总是在少数几条边上进行，这样就会使解的结构过于相似，搜索过程也会停顿下来，算法容易陷入局部最优解而无法跳出。

为了解决这个问题，提出了自适应蚁群算法(Adapt ant colony optimization，简称 AACO)，根据解的搜索情况，动态地自适应调整信息素以及状态转移因子。

在进化前期，设定较大的信息素挥发因子及较小的状态转移因子，使蚁群搜索的随机性增加，使其可以充分搜索到全局最优解的方向。进化一定代数后，蚁群得到最优解的大致方向，此时自适应调整挥发因子及转移因子，减少搜索的随机性，蚁群就可以充分地展开局部搜索，得到最优解。

假设要求Volterra核的有效位为a位，第i个核向量hi可以用a个十进制数来近似表示，就可以构造如下a×i×10+2个“城市”。城市一共有a×i+2层。第一层和最后一层分别仅含一个城市。中间a×i层，从上往下分别表示核向量hi的第一位有效数字、第二位有效数字，…，这些城市中，只有n－1与n层(n∈［2，a+2] )之间的各个城市有连接通路。设n－1层中代表十进制数p的城市与n层代表十进制数q的城市之间的连接上残留的信息量为蚂蚁k在一次循环中的第n层所在的城市用E(k，n)表示。当蚂蚁k由当前所在城市E(k，n－1)=p移动到下一步到达的城市时，根据如下公式选择［5]:

其中，f是［0，1] 区间内的随机数，F0(t)称为为状态转移因子，Srand表示用随机选择来确定下一步要移动到的城市，即根据式(7)计算第n层中每个城市的概率，然后用轮盘赌选择法确定要移动到的城市:

其中，v(p，q)表示从当前层的城市p转移到下一层的城市q的概率。

在式(6)中，状态转移因子F0(t)是一个非常重要的参数。在基于蚁群优化的Volterra核向量辨识方法中，F0(t)是一个［0，1] 上的常数，缺乏自适应。在本文的算法中，F0(t)的选择如下:

其中，ε是正参数，控制F0(t)的上升速度。F0(t)从0逐渐升高到Fmax。

算法初期，F0(t)较小，f有较大概率大于F0(t)。有很大概率选取式(6)的下半部分，即计算转移到每个城市的概率，然后用轮盘赌选择法确定要移动到的城市，体现了随机性。算法后期，F0(t)较大，f有较大概率会小于F0(t)。因此有很大概率选取式(6)的上半部分，即哪条路径上的信息素最大，就选择哪条路径，体现了确定性。

在蚂蚁经过的路径上，按下式进行信息素的更新。

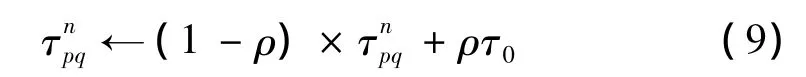
其中，τ0为信息素的初始化值，ρ为信息素的挥发因子。

信息素挥发因子ρ也是一个非常重要的参数，在基于蚁群优化的Volterra核向量辨识方法中，ρ是一个为［0，1] 上的常数，缺乏自适应性。而在本文的自适应算法中，ρ的自适应调整如下［6]:

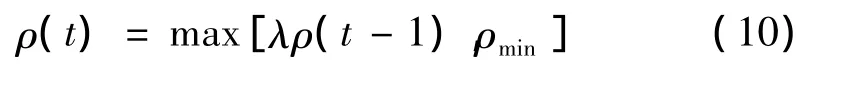
其中:ρmin是预设的ρ的最小值，以防ρ太小导致信息素过度堆积;λ是预设的衰减常数.通过式(10)，信息素挥发因子ρ从最大值随着进化代数的增加，慢慢变小，但又不会低于ρmin，导致信息素过度堆积。与基本蚁群优化算法中的挥发因子选择方法对比可以发现，ρ在进化初期取较大值，增加了搜索的随机性，利于找到全局最优解的大致方向，ρ在进化后期逐渐变小，降低算法随机性，利于局部搜索。显示了本文算法的独特优势。

当所有蚂蚁都走完一遍时，就开始信息素的全局更新。首先根据蚂蚁的行经路径，以及式(5)，计算出蚂蚁k得到的核向量:

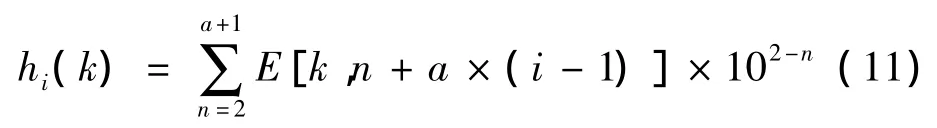
根据目标函数，找出对应函数值最小的最优蚂蚁:

其中，H(k)为第k只蚂蚁的行经路径解码得到的核向量;D［H(k)] 为所求解问题的目标函数。

然后对最优路径上的信息素按式(12)进行全局更新:

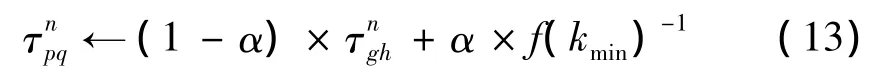
其中 g=E(kmin，n －1)，h=E(kmin，n)，n∈［2，a+2] ，α为信息素的累积速度。它为［0，1] 上的常数。

重复以上步骤直到设定的循环次数或得到的解在一定的循环次数后没有得到进一步的改善为止。

3 基于AACO的Volterra核辨识步骤

由式(2)可以看出，利用式(2)求解Volterra级数核，实际上就是寻求一组n维的核向量使得y－最小。构造如下目标函数:

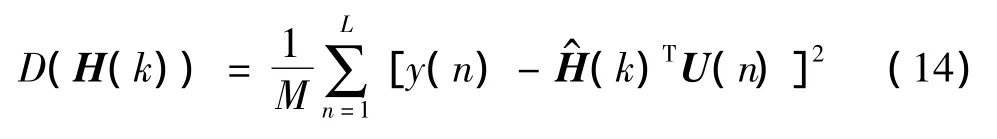
其中，L表示系统的输入输出的数据长度。当目标函数D［H(k)] 取得最小时，即为最优蚂蚁。算法具体步骤如下:

(1)初始化:用一个较小的值τ0初始化所有的

(2)将所有蚂蚁置于第一层唯一的一个城市。即令E(k，1)=0(k=1，2，…，K0)，其中，K0为蚂蚁总数。

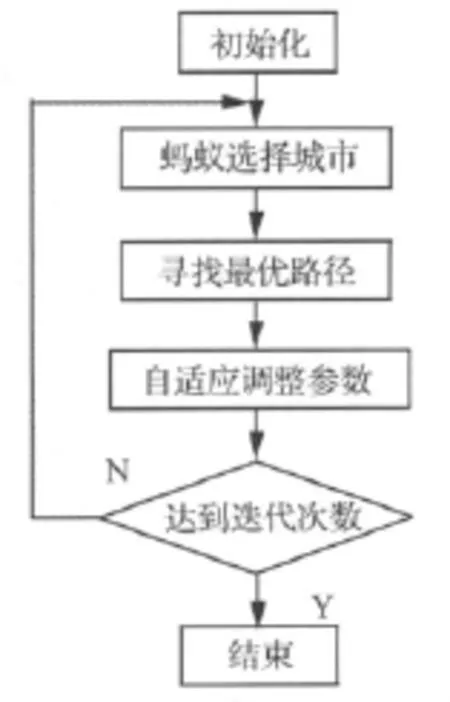
图1 基于AACO的Volterra核辨识算法Fig.1 Volterra kernel identification method based on the AACO

(3)根据式(6)和式(7)得到蚂蚁k在第n层到达的城市E(k，N)。

(5)对每只蚂蚁执行步骤3和步骤4，直到每只蚂蚁都到达最后一层。

(6)根据式(12)找出最优蚂蚁kmin，并用式(13)进行最优路径的信息素浓度更新。

(7)根据式(8)，式(10)自适应调整信息素挥发因子ρ(t)和状态转移因子F0(t)。

(8)判断是否达到设定的迭代次数，达到则输出结果，否则转向步骤2。

4 仿真研究

考虑如下的二阶非线性模型:

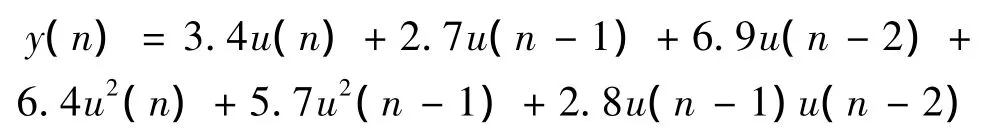
由Volterra理论得，该非线性系统的核矢量H=［3，4，2.7，6.9，6.4，0，0，5.7，2.8，0]

在本文的算法中，选取的参数为 α=0.8，λ=0.95，ε =0.5，a=3，Fmax=0.9，τ0=0.01，K0=40，循环次数为200次。

输入信号为方差为1的白噪声信号。输入、输出叠加不同程度的噪声干扰，采用二阶Volterra级数模型对该非线性系统进行建模。

首先，我们来考察本文算法的辨识精度和抗噪性能，表1给出了无噪声情况下，本文提出的辨识方法得到的Volterra核参数的估计值，为了比较，也给出了基于传统蚁群算法所得到的Volterra核参数的估计值。

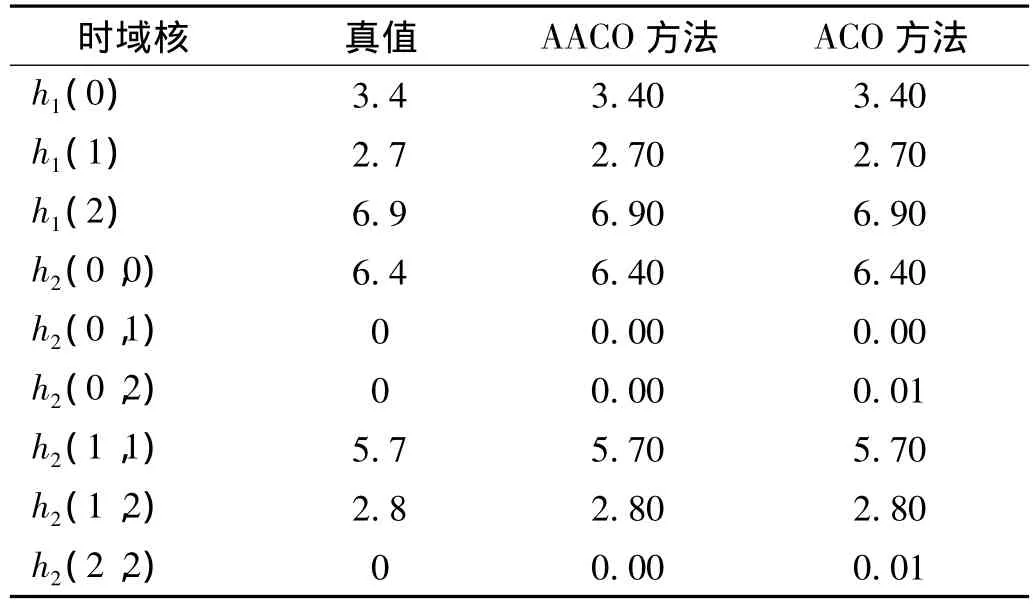
表1 无噪声情况下Volterra核参数的估计值Tab.1 The Volterra kernel estimation under the free-noise environment

由表1可知，在无噪声的干扰下，不论是本文的辨识方法，还是基本蚁群辨识算法，Volterra核参数的估计值和实际真值都完全一致，自适应蚁群辨识算法与基本蚁群辨识算法一样，都得到了非常高的辨识精度。

同时，我们也考察了输入输出端加入不同程度干扰下的Volterra核参数的辨识精度和该算法的抗噪能力，表2给出了信噪比20 dB下，自适应蚁群优化辨识方法和基本蚁群优化辨识方法得到的Volterra核参数的估计值。

由表2可知，在输入、输出端加入20 dB噪声干扰下，Volterra核参数的估计值与真值之间的误差非常小，并没有因为噪声的干扰而对辨识精度产生影响，不论是自适应蚁群辨识算法，还是基本蚁群辨识方法，Volterra核参数的辨识结果还是非常满意的。体现了本文提出的算法具有较强的鲁棒抗噪性。

表2 SNR=20 d B时Volterra核参数的估计值Tab.2 The Volterra kernel estimation(SNR=20 dB)

接下来，讨论本文提出的方法的收敛的稳定性和快速性。图2给出了无噪声的情况下，基本蚁群辨识算法和自适应蚁群辨识算法分别得到的一阶核参数h1(0)，二阶核参数h2(1，2)的收敛曲线。这两个参数的真值分别为 h1(0)=3.4，h2(1，2)=2.8。

图3给出了信噪比20 dB的情况下，基本蚁群算法和自适应蚁群算法分别得到的一阶核参数h1(0)和二阶核参数h2(1，2)的收敛曲线。

从Volterra核的收敛曲线来看，不论是在无噪声环境下，还是在有噪声干扰下，本文算法和基本蚁群算法都具有很好的收敛性和稳定性。而本文方法的收敛速度明显快于基本蚁群算法。其他参数的收敛曲线，同样能反映出AACO算法的优势。这是因为基于蚁群优化的Volterra级数模型的非线性系统辨识方法中，蚁群中多个个体的运动是随机的，当群体规模较大时，要找出一条较好的路径需要较长的搜索时间，另外，在算法中采用了正反馈机理，正反馈过强，容易使优化过程陷于局部极小，正反馈强度过小，则使运行速度过慢，要得到最优解，往往需要很长的的寻优时间。

图2 无噪声时h1(0)，h2(1，2)的收敛曲线Fig.2 The convergence curves of the volterra kernel vectorh1(0)，h2(1，2)under the free-noise environment

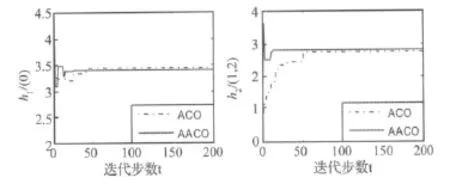
图3 SNR=20dB时h1(0)，h2(1，2)的收敛曲线Fig.3 The convergence curves of the volterra kernel vector h1(0)，h2(1，2)(SNR=20dB)

而基于自适应蚁群优化的Volterra级数模型的非线性系统辨识方法能动态地自适应调整信息素以及状态转移因子，减少搜索的随机性，从而，很好地克服了基本蚁群优化的Volterra核向量辨识方法的不足。

5 结论

本文将自适应蚁群算法引入到非线性系统的Volterra核辨识中，提出了一种基于自适应蚁群优化的Volterra核辨识算法，并与基于蚁群优化的Volterra级数模型的非线性系统辨识方法进行了对比分析，仿真研究表明，不论是在无噪声的干扰下，还是在有噪声的干扰下，基于自适应蚁群优化的Volterra核辨识算法与基于蚁群优化的Volterra核辨识算法都能得到非常好的辨识精度和鲁棒抗噪性能，从收敛曲线来看，即使在噪声的干扰下，两种辨识方法的收敛过程平稳，然而，相对来说，本文提出的基于自适应蚁群优化的Volterra核辨识算法的收敛速度快于基于蚁群优化的Volterra核辨识算法，这是因为本文提出的方法能动态地自适应调整信息素以及状态转移因子，减少搜索的随机性，很好地克服了基本蚁群优化的Volterra核向量辨识方法中因群体规模较大而运行速度过慢的不足。本文的研究为非线性系统辨识提供了一种新的有效方法，具有重要的理论价值和实际应用价值。

［1] Dorigo M，Caro G D，Gambardella L M.Ant algorithms for discrete optimization［J] .Artificial Life，1999，5(3):137 －172.

［2] 唐高松.基于蚁群优化的Volterra级数模型的非线性系统辨识及在故障诊断中应用［D] .郑州:郑州大学，2010.

［3] 魏瑞轩.基于Volterra级数模型的非线性系统辨识及故障诊断方法研究［D] .西安:西安交通大学，2001.

［4] 李 湧.非线性频谱分析理论及其在故障诊断中的应用研究［D] .西安交通大学，1999.

［5] 陈 烨.用于连续函数优化的蚁群算法［J] .四川大学学报，2004，36(6):117－120.

［6] 王 颖，谢剑英.一种自适应蚁群算法及其仿真研究［J] .系统仿真学报，2002，14(1):31－ 33.