分数阶Ver Del Pol-Duffing 系统的非线性动力学行为分析

李媛萍，张 卫

(1.重大工程灾害与控制教育部重点实验室(暨南大学)，广州 510632;2.暨南大学 力学与土木工程系，广州 510632;3.暨南大学 信息科学技术学院电子工程系，广州 510632)

经典的Duffing及van der Pol振子虽然在表达形式上很简单，但是由于具有丰富的动力学特性而极具代表性，它们常常被用来模拟系统的非线性特性。分数导数本构模型由于具有良好的记忆功能，并能在较大频率范围内描述材料的力学性能而成为备受重视的本构模型［1，2]，近年来，用分数导数本构模型描述的分数阶Duffing振子及分数阶van der Pol振子的力学行为已受到科学家们的广泛关注［3－5]，但是关于分数阶 Van der Pol-Duffing耦合振子的动力学行为的研究目前还未见报道。基于此原因，本文构造了一类由分数导数本构模型描述的同时含有Van der Pol系统维持自激振动的非线性阻尼项以及Duffing系统的三次非线性恢复力项的分数阶Van der Pol-Duffing振子，推导了求解分数导数的数值计算方法，结合Runge-Kutta法对非线性振子方程进行数值求解，探讨了该分数阶振子在不同类型荷载作用下的动力学特性。

分数阶Van der Pol-Duffing振子的状态空间描述为:

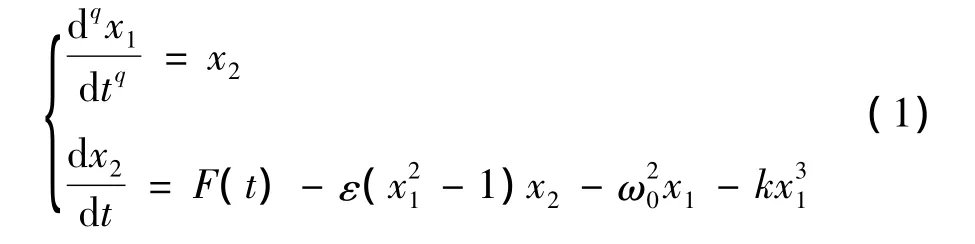
其中，ε，k＞0为非线性控制参数;ω0为自由系统的固有频率;F(t)为外部激励分别为系统任意时刻的位移、速度和加速度;分数导数阶值0＜q＜1。当q=1时，系统(1)即为经典的Van der Pol-Duffing系统。

1 数值计算方法

根据Riemann-Liouville分数导数的定义可知，函数f(t)的 q阶分数导数为［6]:

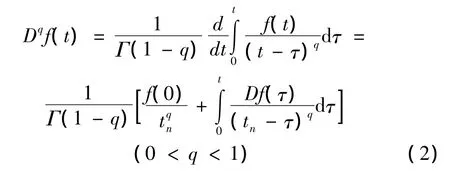
设Riemann-Liouville分数导数在tn=n·Δt时刻的值为 Dqf(t)，取等距积分步长 Δt，则 tn=n·Δt，由于被积函数在积分上限τ=tn=n·Δt时有奇性，导致式(2)不能直接求积。当tn足够大时，如果我们可以把积分区间分成两部分:

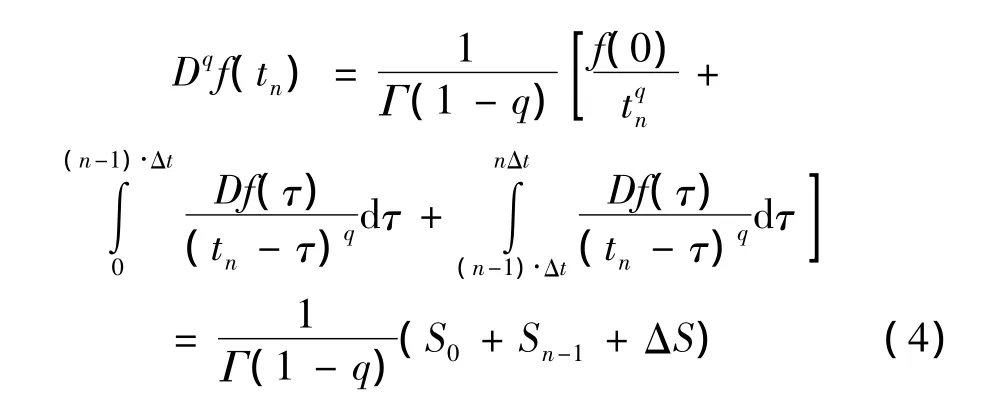
由于ΔS在积分上限处被积函数奇异，需要进行特殊处理，这里采用等距高斯积分法进行线性化处理，设权重函数为，则:

至此分数导数Dqf(t)即可求出。结合Runge-Kutta法即可对方程(1)进行数值求解。

2 自治系统的动力学特性

首先分析自治系统，即F(t)=0。取初值x1(0)=0.3，x2(0)=0.2，并固定系数 ε =5，ω0=1，k=1，改变分数导数阶值q，可以得到不同分数导数阶值下系统的时程曲线、功率谱图及自振周期，分别如图1和图2所示。从中可以看出:随着分数导数阶值的变化，系统的振动周期明显改变，但振幅都趋于极限值2，说明该分数阶振子与经典Van der pol振子一样有极限环存在也伴有自激瞬态过程，无论分数导数阶值如何改变，当t→∞时，振动将趋于定常振动;从功率谱图可以看出:该自治系统存在多个振动频率，假如系统振动的基频以(0＜q≤1)表示，那么在基频的奇整数倍kωq1(0＜q≤1，k=3，5，7，…)处将出现多个谱峰，这说明系统的非线性特性非常明显;同时，随着分数导数阶值的变化，这些谱峰的个数和峰值大小也随之改变，反映了系统的非线性强弱与分数导数阶值密切相关。结合图2可以看出:系统的振动周期随参数q的改变而改变，但并非单调递增或单调递减的关系，当q=1时系统的自振周期最大，而在分数阶区间，自振周期的变化范围很大，其中q=0.4时系统的自振周期最小，仅为q=1时的45%，在q∈(0.3～0.5)区间，系统的自振周期比较接近，都比q=1时的最大值小了50%以上，由此可见，通过改变分数导数阶值的大小可以调节系统的自振特性，而且调节的范围还很大，这一特点正体现了分数导数本构模型的优越性。由于分数导数阶值的变化实质上反映了系统阻尼特性的改变，从上面的分析可知，在参数q∈(0.3～0.5)范围内系统具有较好的阻尼性能。

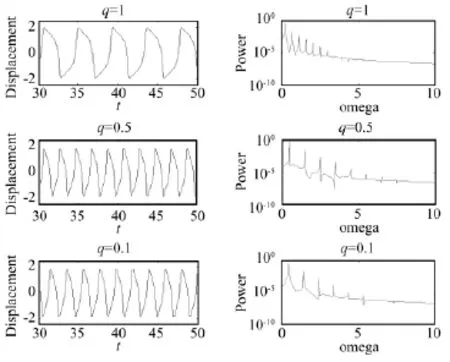
图1 q=1，0.5，0.1 时自治系统的功率谱Fig.1 Power spectra for autonomous system with fractional order q={1，0.5，0.1}

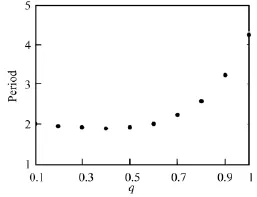
图 2 q=0.1∶0.1∶1 时自治系统的振动周期Fig.2 period for autonomous system with fractional order q=0.1∶0.1∶1

维持初值 x1(0)=0.3，x2(0)=0.2 及系数 ε =1，ω0=1，q=0.5不变，改变非线性刚度系数 k，经数值计算可得到不同非线性刚度系数k下自治系统的相图、时域曲线和功率谱，见图3。从图中可以看出，随着非线性刚度系数的增大，极限环的形状和大小均发生了明显改变，同时系统的振动周期逐渐减小，但振幅仍限定在极限值2以内，说明无论非线性刚度系数k如何增大，系统始终能趋于定常振动且该定常振动是非常稳定的;同时，从功率谱图可以明显看到，随着非线性刚度系数k的增大，系统除在基频和少数奇数倍频处有尖峰外，还出现了分频成分，而且k值越大分频成分越多，反映了系统的非线性特性随k值的增大而显著增强。

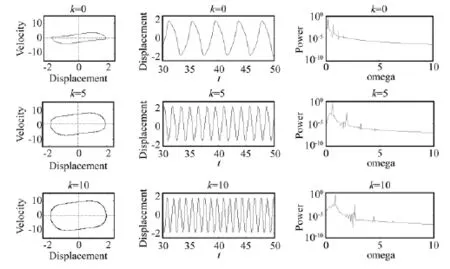
图3 k=0，5，10时自治系统的相图、时域曲线和功率谱Fig.3 Phase diagram(left)and time domain(middle)and power spectra(right)with cubic nonlinear resilience coefficient k={0，5，10}

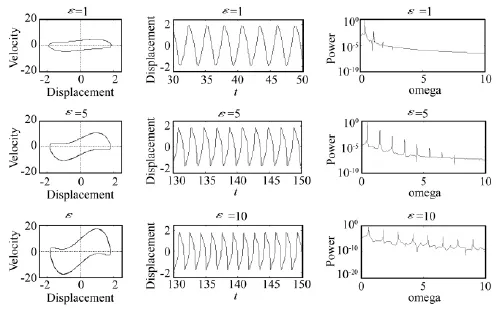
图4 ε=1.5，10时自治系统的相图、时间位移曲线和功率谱Fig.4 Phase diagram(left)and time domain(middle)and power spectra(right)with damping coefficientε =1.5，10

维持初值 x1(0)=0.3，x2(0)=0.2 及系数 ω0=1，q=0.5，k=1不变，改变阻尼系数ε，可得到系统自振特性随阻尼系数的变化规律，如图4所示。从图中可以看出:随着阻尼系数的增大，极限环围绕的面积增大且形状逐渐变得歪扭，功率谱曲线上显示系统振动的倍频分量逐渐增多，同时时间位移曲线的波形逐渐由简谐振动变为张弛振动，但振幅始终限定在极限值2以内，反映系统的非线性特性随着阻尼系数的增大而增强，但无论阻尼如何变化，当t→∞时，系统都将趋于定常振动，这些正是该分数阶振子与经典Van der Pol-Duffing振子的相似之处。

3 周期载荷下的动力学特性

考虑外部激励为简谐荷载F(t)=p cos(ωt)的情形。取参数 ω =1.2，ε =0.1，q=0.5，k1=1=1，同时取系统的初始条件为x1(0)=x2(0)=0，经数值计算可得到系统的位移随外激励幅值变化的分岔图，如图5所示。从图中可以看出:随着外激励幅值的增大，系统将由拟周期振动(见图6)变为周期三振动(见 图7)，最后发展为单周期振动(见图8)。在该范围内未发现混沌现象。

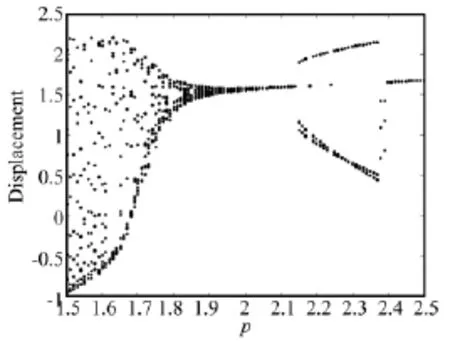
图5 系统的位移随参数p变化的分岔图Fig.5 bifurcation diagram of displacement with varying of parameter p at scope of(1.5，2.5)

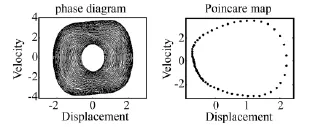
图6 外激励幅值p=1.6时系统的相轨迹和Poincare截面Fig.6 Phase portrait and Poincare map at p=1.6

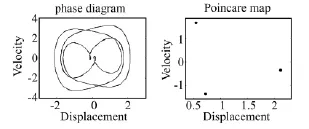
图7 外激励幅值p=2.3时系统的相轨迹和Poincare截面Fig.7 Phase portrait and Poincare map at p=2.3

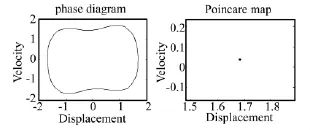
图8 外激励幅值p=2.5系统的相轨迹和Poincare截面Fig.8 Phase portrait and Poincare map at p=2.5

当外部荷载为简谐荷载时，在系统中尽管存在着非线性的影响，但在一定条件下其定常解仍近似于简谐的，基于此，我们可以利用傅里叶变换对其谐波成分进行定量分析。图9是在外激励幅值p∈(1.5，2.5)区间内各次谐波分量的幅值随外激励幅值的变化曲线，计算中共取了五次谐波加以分析，其中0次谐波表示a0的值，从图中我们可以清楚地看出:在拟周期振动区间，前三次谐波为主要成分且幅值波动很大;在单周期振动区间，主要成分为一次谐波;在周期三振动区间，前三次谐波分量均占有较大的比例且波动较小。从图中还可以看出，在整个变化区间，第四、五次谐波分量的幅值均比较小，说明其所占的比例很小，为了简化计算，我们完全可以只取前三次谐波加以分析。

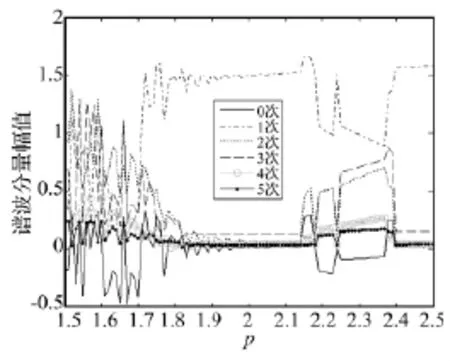
图9 各谐波分量的幅值随外激励幅值的变化曲线Fig.9 Change of harmonic component with excitation amplitude

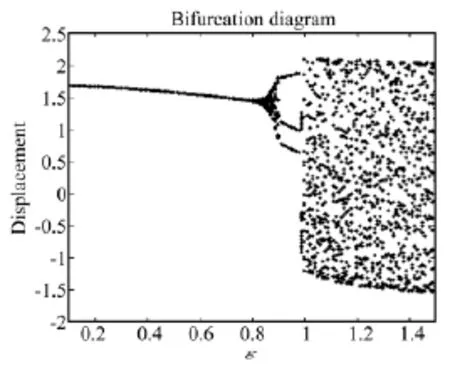
图10 系统的位移随阻尼系数ε变化的分岔图Fig.10 Bifurcation diagram of displacement with varying of damping coefficient at scope ofε

下面探讨在简谐激励下阻尼系数的变化对系统振动特性的影响。假设外激励的幅值和频率分别为p=2.5，ω =1.2，同时假设系统的初始状态为 x1(0)=x2(0)=0，固定参数 q=0.5，k1=1=1，可得到系统位移随阻尼系数ε变化的分岔图，如图10所示。从图中可见，随着阻尼系数的增大，系统将由单周期振动(图11)变为周期三振动(图12)最后发展拟周期振动(图13)。在该范围内未发现混沌现象。

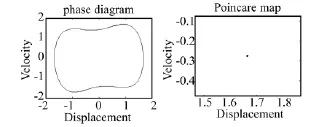
图11 阻尼系数ε=0.15时系统的相轨迹和Poincare截面Fig.11 Phase portrait and Poincare map atε =0.15

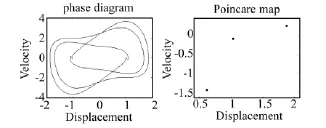
图12 阻尼系数ε=0.95时系统的相轨迹和Poincare截面Fig.12 Phase portrait and Poincare map atε =0.95

图13 阻尼系数ε=1时系统的相轨迹和Poincare截面Fig.13 Phase portrait and Poincare map atε =1

4 地震荷载下的运动特性

最后分析系统在地震荷载作用下的振动特性。地震波的实质是一种非平稳信号，因此在地震作用下结构的反应无疑也是非平稳的，从而使得在非线性分析中普遍采用的相图、Poincare截面以及分岔图等分析方法已不再适用，本文采用信号处理中常用的快速傅里叶变换法进行处理。选取EL－centro地震波的南北分量作为输入(加速度峰值为341.7 m/s2，取样时间为前30 s，取样频率为50 Hz)，其加速度时程曲线和相应的功率谱见图14，从其功率谱图可看出，其能量主要分布在0 Hz～5 Hz的范围内。

固定参数 ε =0.1，k1=1=1，并设系统的初始状态为x1(0)=x2(0)=0，改变q，可得到系统在不同分数导数阶值下的动力反应特征。为节省篇幅，本文仅示意出分数导数阶值分别为 q=0.1，0.5，0.9 时系统动力反应的时域曲线和功率谱，见图15。从图中可以看出:EL－centro南北波经过该系统之后，输出信号的频率范围和幅值均大大减小且主要集中于0.5 Hz～1 Hz范围内，说明大部分的输入能量被消耗;其中，当q=0.5时系统输出信号的功率谱的幅值最小，同时其位移幅值随着时间的增加逐渐衰减，说明q=0.5时系统输出的动力反应最小，究其原因正是因为当q=0.5时系统的阻尼较大，从而消耗掉更多的能量。

图14 EL-centro地震波时程曲线及功率谱Fig.14 Time domain and power spectra of EL-centro wave

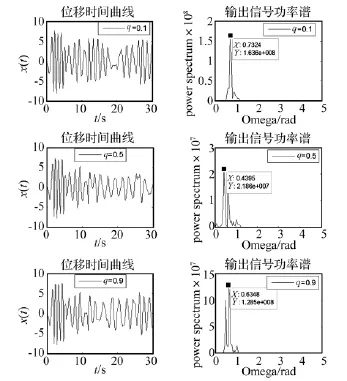
图15 q=0.1，0.3，0.5，0.7，0.9 时系统动力反应的时域曲线和功率谱Fig.15 Time domain and power spectra with fractional order q=0.1，0.3，0.5，0.7，0.9 under seismic load

5 结论

本文引进分数导数本构模型模拟系统的阻尼特性，构造了一类同时含有Van der Pol系统维持自激振动的非线性阻尼项以及Duffing系统的三次非线性恢复力项的分数阶Van der Pol-Duffing振子，通过数值计算探讨了该系统在不同荷载作用下的振动特性，可以得到如下结论:

(1)该非线性振子具有与经典Ver Del Pol系统相似的自激振动特性，同时分数导数阶值的变化能改变系统的自振周期;在q∈(0.3～0.5)区间，系统的自振周期比整数阶系统减小一半以上。

(2)随着阻尼系数和非线性位移系数的增大，系统的非线性增强。

(3)在简谐荷载作用下，随着外荷载幅值的增大，系统由拟周期振动变为周期三振动最后发展为单周期振动。

(4)在简谐荷载作用下，随着阻尼系数的增大，系统由单周期振动变为周期三振动最后发展为拟周期振动。

(5)在地震荷载作用下，通过调节分数导数阶值可以改变系统的阻尼性能从而改变输出的能量。

［1] Ge Z M，Ou C Y，Chaos in a fractional order modified duffing system［J] .Chaos Solitons ＆ Fractals，2007，34(2):262－291.

［2] 李根国，朱正佑，程昌钧.非线性粘弹性Timoshenko梁动力学行为的分析［J] .力学季刊，2001.22(3):346－352.

［3] Gao X，Yu J B.Chaos in the fractional order periodically forced complex Duffing's oscillators［J] .Chaos Solitons ＆Fractals，2005.24(4):1097 －1104.

［4] Cao J，Xie H，Jiang Z.Nonlinear dynamics of duffing system with fractional order damping［J] .Hsi-An Chiao Tung Ta Hsueh/Journal of Xi'an Jiaotong University，2009，43(3):50－54.

［5] Barbosa R S，Machado J A T，Ferreira I M.Dynamics of the fractional-order van der pol Oscillator［C] .IEEE Transactions on Industrial Electronics:373－378.

［6] 张 卫，徐 华，清水信行.分数算子描述的粘弹性体力学问题数值方法［J] .力学学报，2004，36(5):617－622.