线性剪切模量地基的地震响应分析

侯凯贤，葛广全

(西安建筑科技大学土木工程学院，陕西西安710055)

由于地震激发引起地基振动，从而使地基产生随时间变化的位移、速度、加速度、内力和变形等，统称为地基的地震响应。地基上的质量因加速度的存在而产生的惯性力称为地震作用。地基的地震响应取决于地震特性和地基特性，特别是地基的动力特性(如自振周期与阻尼)。

本文的目的是研究线性剪切模型地基的地震响应问题。确定其自振频率、振型函数、参与系数及稳态动力响应的封闭型解析表达式，进而计算得出地基土的相对位移、剪应变、剪应力以及绝对加速度响应表达式。并且利用数值算法结合计算机求得其在基岩输入下的最大反应。

1 基本理论

1.1 建立模型［1］

当土层的物理力学性质在水平上为均匀时，在基岩面上水平地震动¨ug(t)的作用下，可以认为土层沿整个高度的质量密度ρs是均匀的，且土层只受水平方向地震动的影响，不考虑竖直方向地震运动。土层的位移也只受水平方向的剪切位移，没有弯曲位移，这样就可以将土层作为一个具有非均匀剪切模量的剪切梁，如图1所示。从图1(a)中取出一单元薄土层dz，如图1(b)所示，由作用在单元体上的力的平衡关系，得:

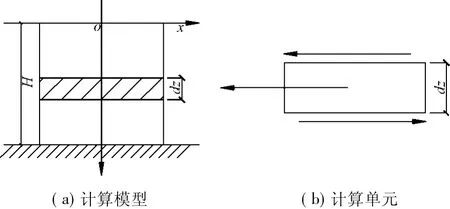
图1 土层计算模型

1.2 动力学方程推导及定解条件

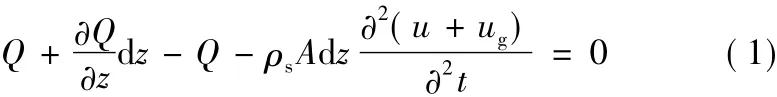
式中:Q为土层间的剪力;u为土层的位移。

将式(3)代入式(2)得:

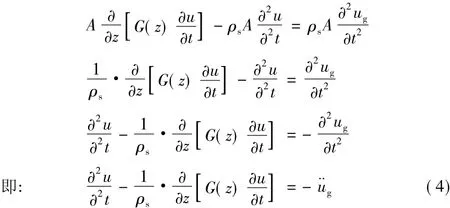
如果在上述计算中考虑土层的粘滞阻尼力，则可将式(4)进一步写为:

式中:cs为土的粘滞阻尼力。

式(5)就是场地土地震时的动力基本方程，它的解答应满足以下定解条件。

初始条件:

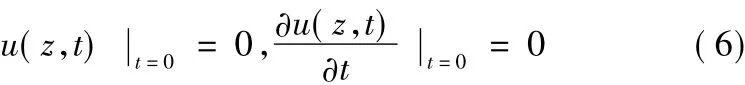
边界条件:

2 地基解的求解

2.1 频率方程建立和求解及振型函数的获得

利用分离变量法，设:

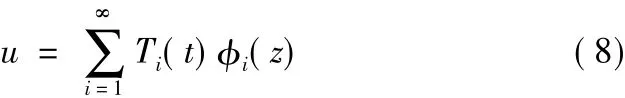
式中:ηi为振型参与系数。

将式(8)代入式(5)，进行变量分离，两边除以φi(x)得:

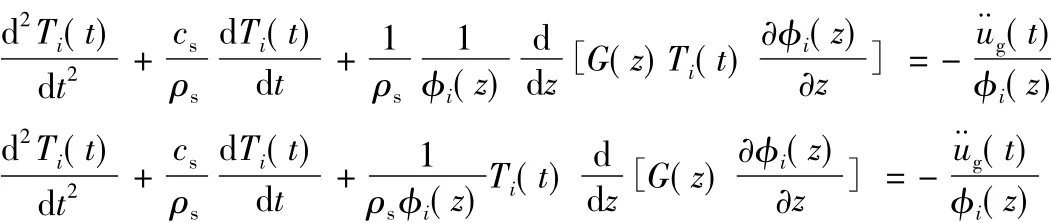
即:

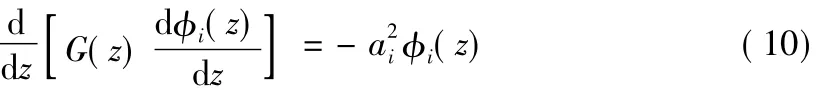
式中:a2i为待定常数。

由式(6)和式(7)可得其定解条件为:

当已知剪切模量的表达式以后，代入以上方程就可以得到相应的解答。

下面求解式(10)。为此将式 G(z)=G0+mz代入式(10)，得:

代换x=G0+mz，则式(14)成为:

令αi=ai/m，于是上式可进一步写成

式(15)为二阶常微分方程，即:

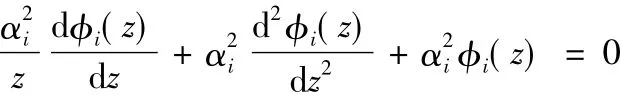
(两边除以α2i，再乘以 z2)

此式是n为零的贝塞尔(bessel)方程，其通解可以表示成为:

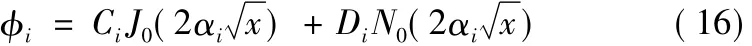
式中:J0和N0分别是零阶第一类贝塞尔函数和零阶第二类贝塞尔函数。

将式(16)代入边界条件式(13)可得:

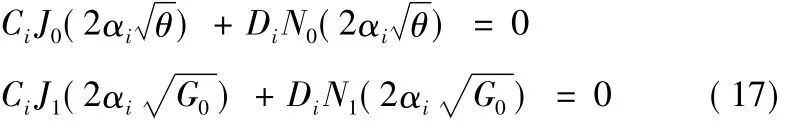
式中:θ=G0+mH;J1和N1分别是一阶第一类贝塞尔函数和一阶第二类贝塞尔函数［9］。

由式(17)中的系数行列式等于零，得到确定ai的方程为:

若令:

则

于是式(18)可写为:

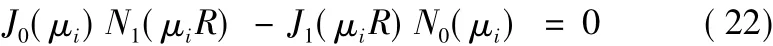
式(22)的根μi可以从相应的手册中查出或通过计算机解出。当μi确定后，ai即可由下式解出:

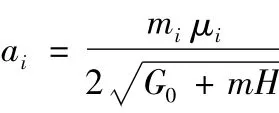
其次，从式(17)中的第二式得:

将其代入式(16)中可进一步得到:

式中:

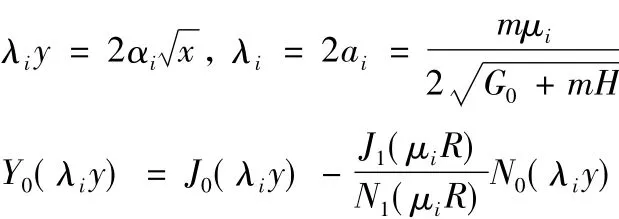
2.2 确定振型参与系数ηi

贝塞尔函数正交性:

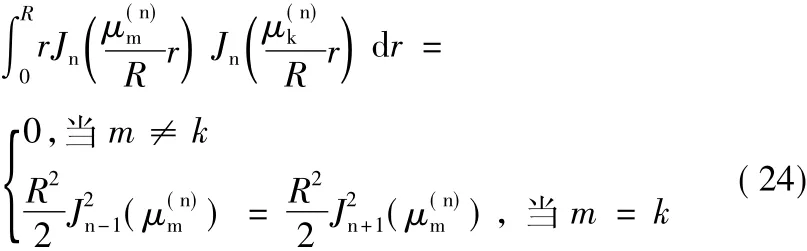
η的求解:将式(9)两端同乘以 λyY(λy)，并对 y

ij0j从0到1进行积分。根据贝塞尔函数的性质，右端可得:

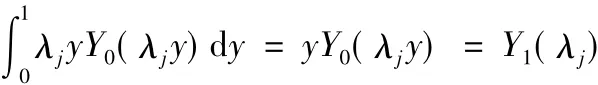
左端

当i=j时

当 i≠j时

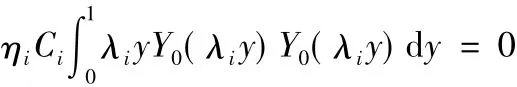
从而可得

2.3 相对位移反应的计算

2.3.1 Ti(t)函数的求解

求解式(11)，将其改写为:

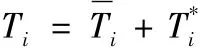
于是式(11)的通解为:

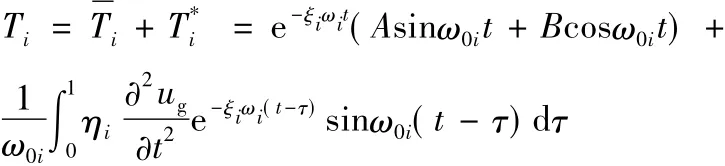
将其代入定解条件式(12)中，得A=B=0。所以该问题的解答为:

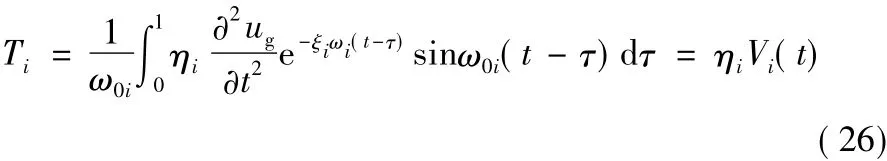
式中:

综合以上各式，得到式(8)的解为:

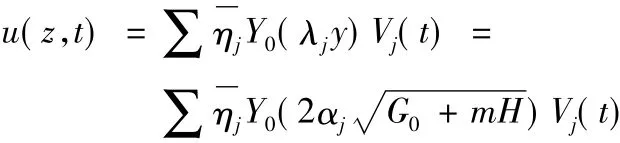
式中:

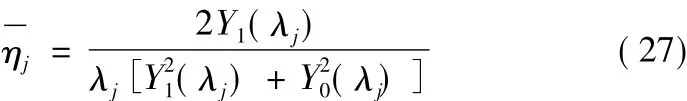
式(27)即为剪切模量随深度均匀变化时场地土相对位移反应的计算公式。

其中对应的齐次解为:

式中:ω0i=ωi√1－ξ2i为第i振型自振圆频率。

特解T*i可以根据杜哈梅(Duhamel)积分求得，即:

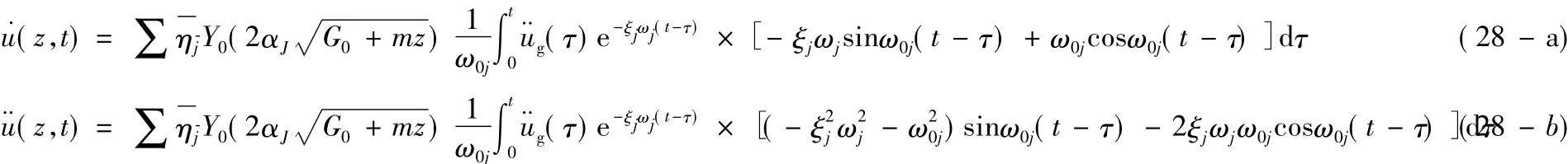
当阻尼较小时，式(28)可以近似写为:

式中:ηaj=－ω2jηj称为绝对加速度振型参与系数。

由式(27)可得到土层的剪应变为:

2.3.2 地震反应

由于地面水平运动¨ug(t)不是一个规律的函数，要把真实的强震记录¨ug(t)不加处理地放入公式进行积分几乎是不可能的。因此，多采用另一种途径，即用数值分析的方法来计算地震反应。特别是计算机技术的发展，为这一方面提供了极其有利的条件。目前用的较多的有线性加速度法、威尔逊(Wilson)－θ法及龙格－库塔(Runge－Kutta)法。

2.3.3 龙格－库塔法及算例［7］

龙格－库塔法:在逐次积分法中，龙格－库塔法是最简单的，它把动力方程化为两个一阶微分方程组求解，计算的精确度也比较高。

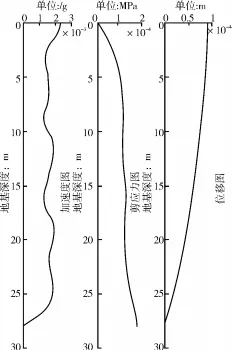
算例:某场地土层厚度H=28 m，土层的密度ρs和s波速¨ug(t)都是实测值，剪切模量G由G=G0+mz算出，该场地土的G0和m分别为G0=25.5 MPa，m=0.52857 MPa，土的密度取平均值ρs=1 600kg/m3，地基土的阻尼比为ξ=0.01，利用上述数据算得的土层最大期望反应(相对位移、相对剪力和绝对加速度)见图2。计算前8阶频率为(单位rad/s):

3 结论

本文选择地面上一点作为坐标原点，建立了线性剪切模量地基响应的计算模型，把基岩输入地震化作为边界条件静止不动而在计算域各点上作用着惯性力的问题进行计算，在给定的时间域中得到了基岩在任意输入地震作用下的解析解。利用数值方法，通过对一算例的计算得出在土层剪切模量为线性变化的情况下，地基土的最大反应图(相对位移、绝对加速度和剪应力)。

［1］黄义，门玉明．结构－地基相互作用系统可靠性分析［M］．西安:陕西科学技术出版社，2000

［2］张为民，黄义，王春玲．成层地基一维土层地震反应解析［J］．西安建筑科技大学学报，2003，35(2)

［3］王春玲，黄义．剪切模量是幂函数的成层土的地震随机反应［J］．应用力学学报，2004，21(2):21－26

［4］高玉峰，金建新，谢康和，等．成层地基一维土层地震反应解析解［J］．岩土工程学报，1999，21(4):488－500

［5］栾茂田，金崇磐，林皋．非均质地基振动特性及地震反应分析［J］．大连理工大学学报，1992，32(1):81－87

［6］刘延柱，陈文良，陈立群．振动力学［M］．北京:高等教育出版社，2002

［7］朱伯龙，张琨联．建筑结构抗震设计原理［M］．上海:同济大学出版社，1994

［8］Ikuo Towhata．Seismic wave propagation in elasic soil with continuous variation of shear modulus in the vertical direction［J］．Soil and Foundation，1996，36(1):61－72

［9］汪德新．数学物理方法［M］．北京:科学出版社，2006

［10］吴湘兴．建筑地基基础［M］．广州:华南理工大学出版社，1997

［11］吴家龙．弹性力学［M］．北京:高等教育出版社，2001

［12］David G．Luenberger．Introduction to Dynamic Systems Theory，Models，and Applications［M］．United States:John Wiley ＆ Sonsc Inc，1979

［13］Ray·W·Clough，Jose ph·Penzien．Dynamicsof Structures［M］．United States:McGraw－Hill，1975