基于制造任务参数距离模型的协同制造链优化构建

程方启 叶飞帆

1.浙江工商职业技术学院，宁波，315012 2.宁波大学，宁波，315211

0 引言

在网络化制造环境下，产品制造的各个环节可能分布在不同的区域、企业，为保证产品制造的高效、低成本，获得制造任务的企业需要寻求能满足需求的协作企业的协同。这种跨地域、跨企业的协作，需要一种能够快速建立协同制造过程链的途径。网络环境下建立协同制造过程链的方法，大多是根据制造任务选择所需的资源[1]，分析制造资源所在企业的信誉、生产负荷等状况。制造任务的结构一旦确定，较少考虑通过调整改变制造任务的参数来适应市场上的制造资源情况，而主要关注承担制造任务的制造资源能够完成协同任务的完成时间、完成质量、完成成本等[2]。虚拟企业或虚拟联盟作为21世纪重要的生产经营与市场竞争的企业组织形式，将地理上和组织上分散的企业组织起来，通过企业间的有效协作而实现“共赢”的目标，以实现企业间制造资源的共享与优化配置[3]。Fischer等[4]提出了一种基于“能力单元”的虚拟企业模型——水平型区域制造网络，以改善并提高中小企业的竞争力，并根据制造任务寻找可适用的制造资源。Yao等[5]针对网络环境中复杂零件的制造问题，提出了物理制造单元与逻辑制造单元的概念，在制造任务与制造资源确定后应用遗传算法计算最优可执行加工路径。吉峰等[6]提出了一种应用UML建模语言描述的网络制造服务模式——协同制造链，利用蚁群算法对其优化问题进行求解。可见，协同制造过程的快速构建需要解决制造任务与制造资源的规划、过程优化模型的构建及优化方法的选择等问题。

构建虚拟企业或协作联盟是制造任务与制造资源之间相互协调、不断调整优化的演化过程。笔者在以上研究的基础上，从协同制造过程链的角度出发，提出了协同制造单元（collaborative manufacturing unit，CMU）、制造任务单元（manufacturing task unit，MTU）及协同制造链（collaborative manufacturing chain，CMC）的概念，从制造任务参数优化角度出发，基于制造任务参数距离建立了协同制造链的优化模型，应用自适应遗传算法进行优化计算，并对实例的结果进行了分析。

1 协同制造链相关定义

（1）协同制造单元。CMU是由同一个企业内的制造设备、工装附件以及相关软资源组成的、具有一定核心能力的制造单元，具有高度专业化及对外协作能力，在法律及经济上自治。一个CMU属于一个企业；而一个企业可以组建一个或多个CMU，处于网络中的所有CMU构成了一个制造能力库。

（2）制造任务单元。根据复杂零件的制造加工任务的制造特性及工艺规划可将其分解为多个MTU。一个MTU可以包含一个或多个制造加工工序，是对外协作任务的基本单位。由于制造工艺路线的多样性，因此一个MTU可以由不同的CMU来承担，这些CMU可以是不同类型的，也可以是同一类型的；一个CMU也可以承担一个或多个MTU。

（3）协同制造链。针对复杂零件制造任务分解得到的MTU分别由网络中合适的CMU所提供的制造服务完成，各MTU之间按照约束关系组合成一条整体的制造服务链，称之为CMC，可描述为

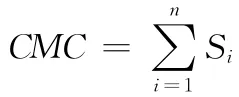
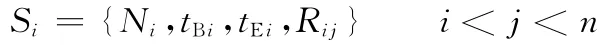
式中，Si为CMC中的第i个制造服务；Ni为制造服务Si的ID；tBi为制造服务Si的开工时间；tEi为制造服务Si的完工时间；Rij描述制造服务Si与下一个制造服务Sj的时序关系；n为制造服务的数量。

图1为CMC示意图。

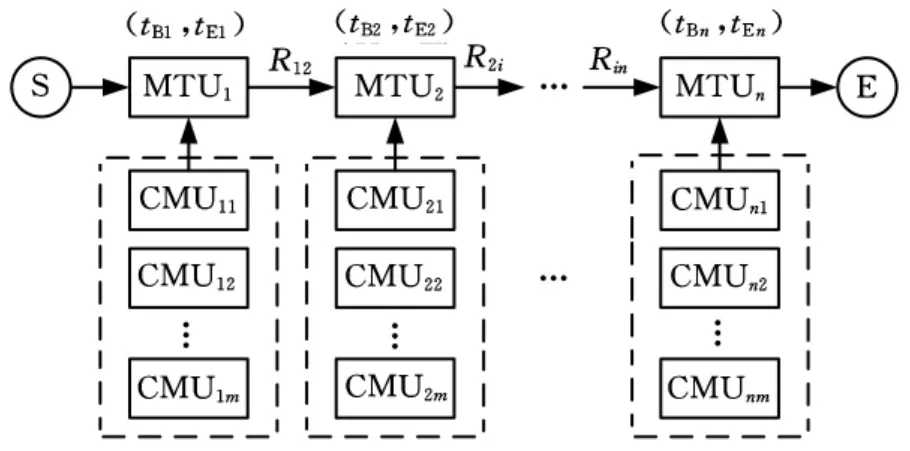
图1 CMC示意图

2 协同制造链优化过程的参数描述

CMC的优化过程涉及的影响因素较多，为深入研究其优化过程，对制造任务性能参数进行形式化的描述。

2.1 制造任务参数

制造任务性能参数（parameters of manufacturing task，PMT）描述制造任务属性，反映制造任务的性能指标，主要包括制造时间、执行成本、成品率等。如果CMC包括n个制造子任务，则制造任务性能参数可表示为

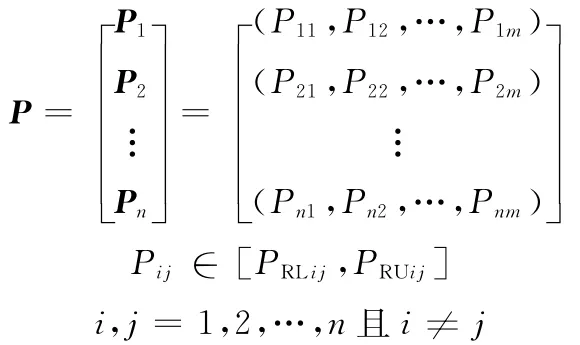
式中，Pj为制造任务的第j个参数；m为参数的数量；Pij为第i个制造任务的第j个参数；PRLij、PRUij分别为第i个制造任务的第j个参数取值区间PRij的下限和上限。

2.2 制造任务预期参数

在CMC的构建过程中，针对制造任务，盟主CMU经过市场调研，初步预先确定能够完成制造任务的参数指标，称之为制造任务预期参数（prospective PMT），它可表示为

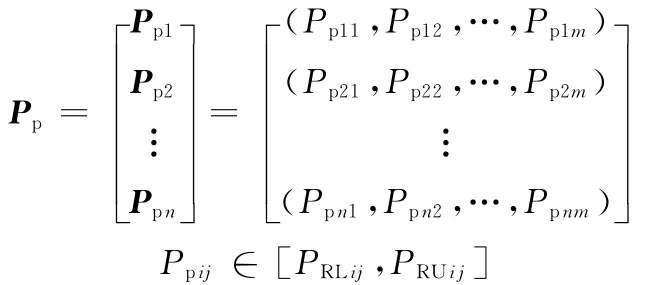
式中，Ppij为第i个制造任务的第j预期参数。

2.3 制造任务完成参数

在CMC的构建过程中，针对 MTU，候选CMU针对具体的制造子任务，结合自身制造资源的属性特征，提出的任务完成性能指标称为制造任务完成参数（completed PMT），它可表示为

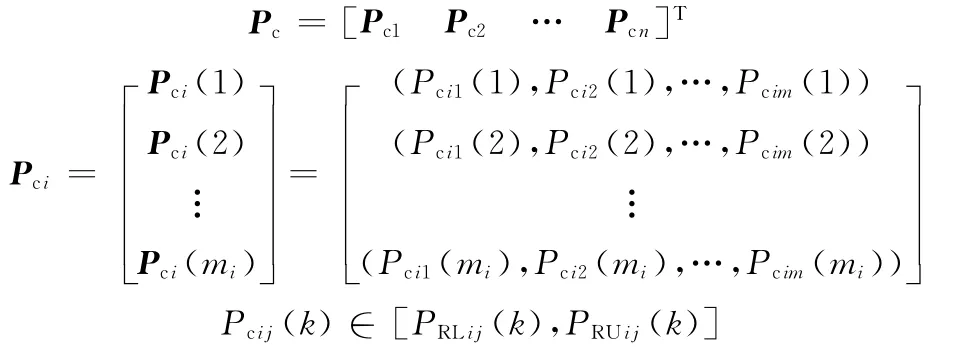
式中，Pcij（k）为第k个候选CMU的第i个制造任务的第j个完成参数，k＝1，2，…，mi。

2.4 最优制造任务参数

在CMC的构建过程中，针对制造任务，结合制造任务完成参数与预期制造任务参数，优化任务参数的最优解为最优制造任务参数（optimal PMT），它可表示为

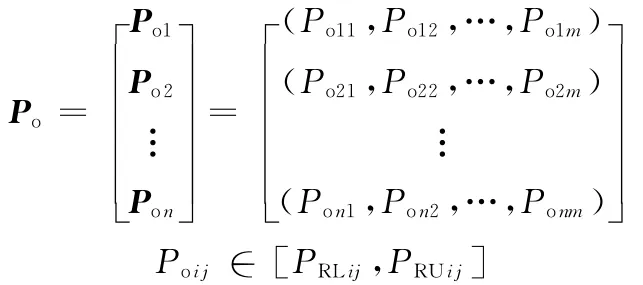
式中，Poij为第i个制造任务的第j个最优参数。

3 协同制造链优化建模

3.1 协同制造链优化构建过程分析

在构建CMC的过程中，盟主CMU在市场上寻求协作CMU来完成制造任务，并致力于CMC整体运行的最优化。盟主CMU根据产品制造任务的具体特性，考虑到自身制造资源的不足，寻找协作CMU来共同完成制造任务。盟主CMU对制造任务进行分解进而形成n个制造子任务，针对制造子任务i，盟主CMU提出完成制造子任务i的预期参数Ppij；市场中有mi个候选CMU对制造子任务i进行响应时，每个候选CMUk提出自己的制造任务完成参数Pcij（k）。CMC任务参数优化的目标就是根据盟主CMU与候选CMU双方的参数，建立适当的优化数学模型，得到适当的制造任务参数。CMC优化构建过程分析见图2。

3.2 协同制造链优化建模

在CMC的构建过程中，当盟主CMU提出制造任务完成参数Pc时，针对第k个候选协作CMU所提出的Pci，我们可以考察任一制造任务参数P与Pci之间的参数距离。参数距离描述两个多维参数指标的平均偏差。对所有候选协作CMU，计算P与Pc中每个Pc（k）的平均参数偏差。平均参数偏差表示制造任务完成参数Pc相对于任一制造任务参数P的分布情况，即Pc整体所表现出来的稳定与波动、集中与离散的程度。显然，该值越小，说明Pc相对于P的分布越集中，P所代表的制造任务参数值越接近于市场中实际制造资源的供给情况。

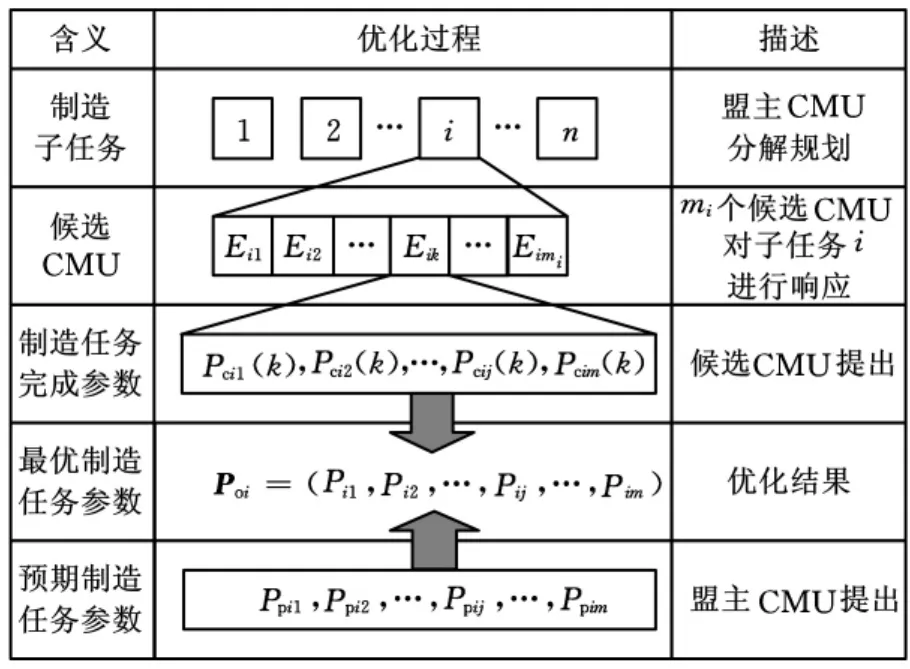
图2 CMC优化过程分析

为了便于CMC参数优化建模，这里引入向量、向量范数的概念。衡量两个多维向量之间的距离有多种方法，如街区距离、欧氏距离、明考夫斯基距离等。由于欧氏距离的概念清晰、简单，因此，本文应用欧氏距离来度量多维向量之间的距离。

3.2.1 制造任务参数向量的欧氏距离

在CMC的构建过程中，对于任一制造任务的参数Pi与第k个候选协作CMU所提出的制造任务完成参数Pc（k），如果将它们基于制造任务的序数展开为向量形式，那么可得到这两个向量之间的加权向量欧氏距离，记为di（P）。

令λj为第j个任务性能参数的权重系数，

则得到

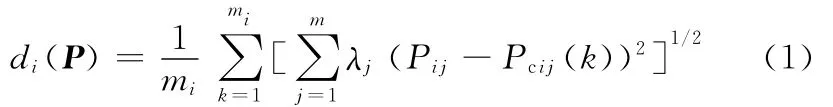
3.2.2 制造任务参数优化目标

在CMC的构建过程中，对于所有n个制造子任务的参数P与对应的每一个Pci中的di（P）的总和，设为制造任务参数优化目标，记为f（P）。根据制造任务参数、制造任务完成参数以及欧氏距离的概念，令wi表示第i个制造子任务的权重系数，则得到

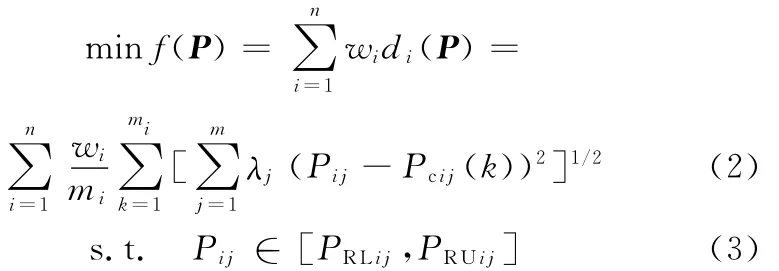
4 基于自适应遗传优化算法的求解

4.1 编码机制和模型转换

相对于二进制编码，实数编码直观性好，避免了位编码与实参数间的转换操作，以及由此引起的量化误差，并在理论上能以任意精度取得结果；同时实数编码形式可以使编码和问题的解具有明显的对应关系。因此，本文采用实数编码机制（见表1）。

表1 编码机制

对于包含n个MTU的制造任务，将从1到n所有MTU所对应的PMT按照升序展开，形成一条染色体。每条染色体就代表一种选择，可以表示如下：

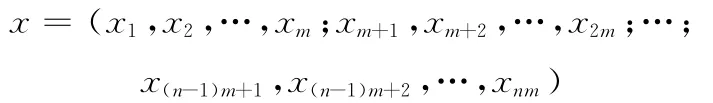
则在约束条件（式（3））下，目标函数（式（2））可表述为优化函数：

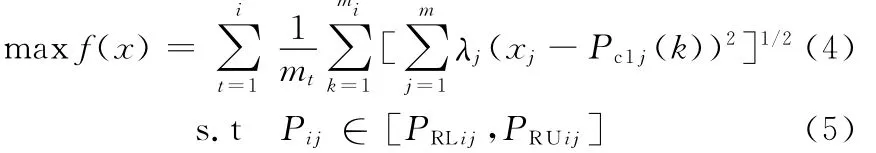
通过模型转换，得到的式（4）与式（5）比原来的式（2）与式（3）更清晰、更具体。对于较大规模的组合优化问题，传统的数学方法难以获得优化解，但是应用遗传算法却相对容易。

4.2 遗传算子设计

标准遗传算法采用固定的交叉算子与变异算子，这严重影响了算法的收敛性，易陷入局部最优。为了提高算法的收敛速度。本文采用根据适应度值自适应改变交叉算子与变异算子的机制。进行选择操作时，按适应度值大小，保留本代最优个体进入下一步操作（交叉或变异），而不是直接进入下一代，其余个体按轮盘赌进行随机选择。

遗传算法解的搜索是在适应度值的引导下进行的，所以应该根据适应度值的大小动态调整交叉与变异算子，加快收敛速度。交叉概率pc越大，产生新个体的速度就越快；然而，pc过大时遗传模式容易被破坏，适应值高的个体不容易保持，但是pc过小，搜索速度会变慢。如果变异概率pm过小，就不容易产生新个体；过大则搜索过程成了纯粹的随机搜索。如果用固定的交叉与遗传算子，对于给定的优化问题，需要不断调整来确定其值。基于此，本文提出自适应动态调整交叉与变异算子的机制。pc与pm按以下公式进行自适应调整：

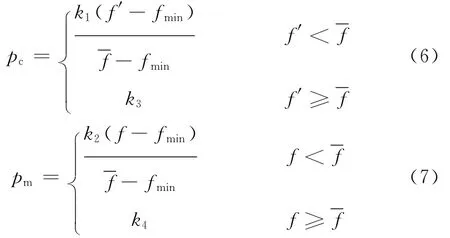
式中，fmin为种群中最小的适应度值；f为每代种群的平均适应度值；f′为要交叉的2个个体中较小的适应度值；f为要变异个体的适应度值；k1，k2，k3，k4∈ [0，1]。

本文采用的自适应遗传算法在群体收敛至局部极值附近时，增大变异概率，从而增加群体多样性，跳出局部解；当群体在解空间分散时，则增大交叉概率，加快收敛速度，这样既保证了向全局最优解逼近，又保证了一定的收敛速度。

5 协同制造链优化实例及结果分析

优化仿真试验以某金属制品公司一种产品的制造为应用实例进行分析，该产品为金属密封圈，试验中的数据来源于该企业的生产计划部门。盟主CMU分析产品制造过程，结合自身制造资源状况，需要寻找其他CMU构建CMC进行协作制造。

针对该产品CMC构建过程，盟主CMU将该制造任务分解为5个可以独立进行市场运作的MTU，它们分别是开模、精密铸造、热处理、精加工与检验，记为 （T1，T2，T3，T4，T5）。每 一 项MTU有3个性能参数：制造周期MT、制造费用MC、成品率MQ。

盟主CMU经过市场前期调研，分别就各MTU与有协作意向的CMU建立了联系。盟主CMU根据自身制造资源的综合条件，结合制造任务自身特性及需求，提出了对各MTU的完成指标参数。所有MTU对应的候选协作CMU及其完成参数Pc见表2。

盟主CMU根据制造任务的特性及需求，提出了制造任务参数值域（表3）和预期制造任务参数（表4）。

PMT的权重可以根据对CMC运行的风险及其影响来评价。MTU的权重应该根据具体的市场环境、任务的结构及参数来确定。本例中，制造协作CMU的权重与MTU的权重取值见表5。

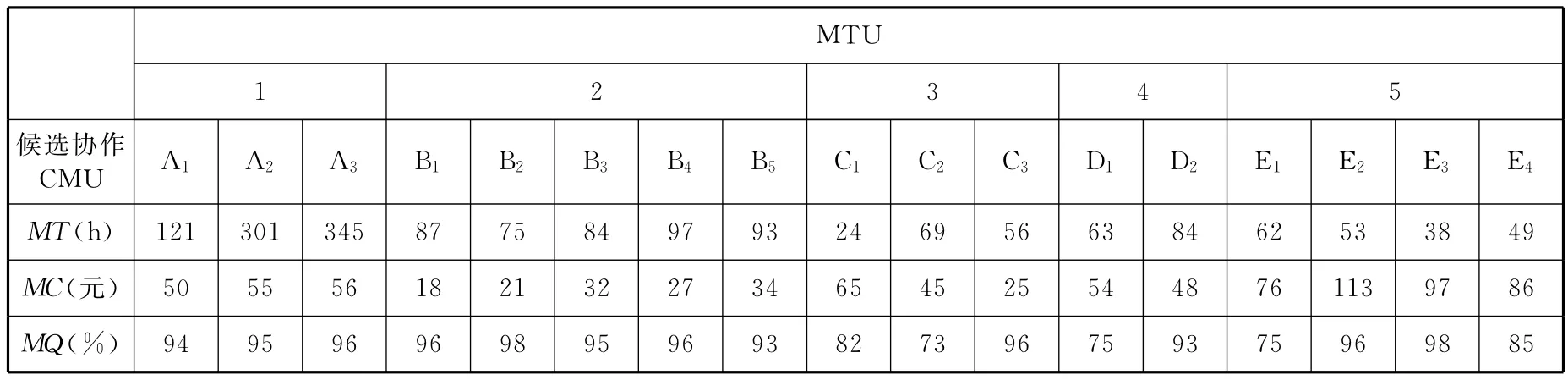
表2 候选协作CMU及完成参数Pc

表3 PMT的取值区间值域

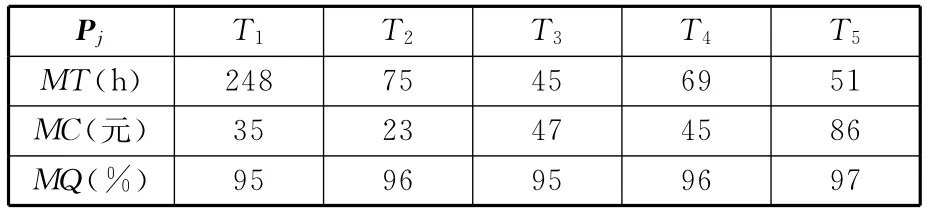
表4 预期PMT Pp

表5 权重值

根据遗传算法的染色体编码机制，确定

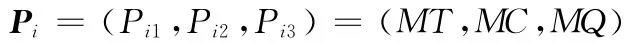
则由5个MTU构成的制造任务参数序列为

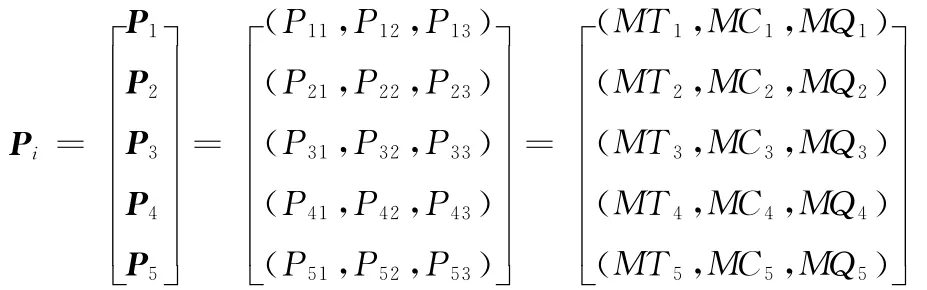
那么，染色体可以表示为

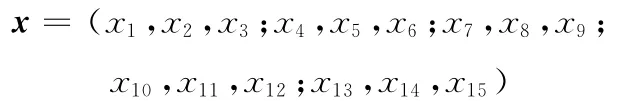
遗传算法的相关参数取值具体见表6。

表6 遗传算法参数取值

计算条件如下：Pentium 4主频2.66GHz的CPU、512MB内存、WinXP操作系统、MATLAB 7.0软件。采用实数编码的自适应遗传算法进行CMC性能参数优化，得到目标函数的最优值，即min f（P）＝4.5616。得到的最优解为

其CMC参数优化仿真曲线在迭代次数接近300时趋于稳定，见图3。

图3 自适应遗传算法迭代过程

预期制造任务参数Pp与获得的最优制造任务参数P＊的对比见表7。根据理想解（PIS）与负理想解（NIS）所确定的PMT的取值范围如图4中阴影所示，用折线连接的点表示最优解P＊。

表7 PMT Pp与P＊的对比

分析遗传算法计算过程的搜索空间，并与应用TOPSIS方法[7]的搜索空间相比较。TOPSIS法是一种常用的有限方案多目标（属性）决策分析法。然而，TOPSIS法有不容忽视的不足之处：与“理想解”欧氏距离更近的方案可能与“负理想解”的欧氏距离也更近，按相对欧氏距离对方案作排序的结果并不能完全反映出各方案的优劣性。

应用TOPSIS于本例中，理想解（PIS）表示

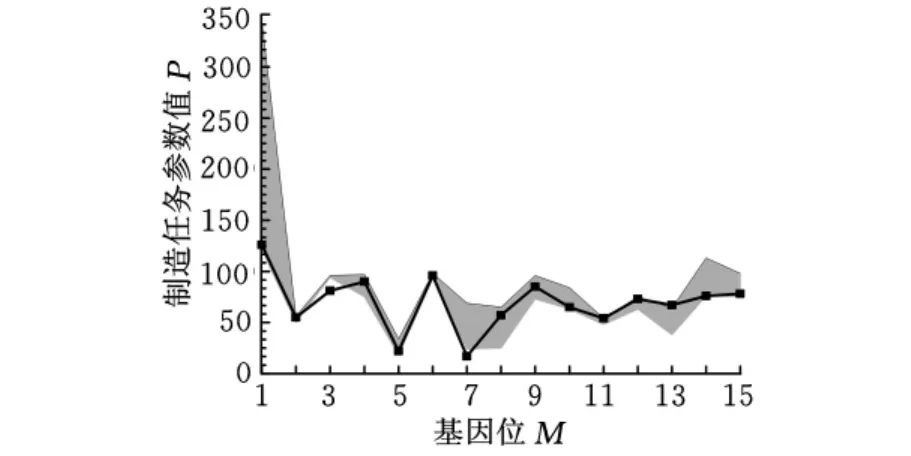
图4 TOPSIS中值域与P＊的对比

从而，根据理想解与负理想解所确定的PMT的取值范围如图4中阴影所示。用折线连接的散点表示最优解P＊，可以看出，基因位3与7处的取值并不在阴影区间内。表明CMC的协作双方可以通过协商，调整响应制造子任务的制造成本与制造周期。同时也表明自适应遗传算法扩大搜索区间的方法优于TOPSIS方法。

针对优化仿真结果，进行分析如下：

（1）对比表3与获得的最优解P＊，可以发现

（2）从表7可以看出，MTU1、MTU3与MTU4状况相似。最优解P＊的制造成本MC均高于对应的预期制造任务参数Pp的制造成本MC，而制造周期与成品率均低于预期制造任务参数Pp的对应参数值。这表明上述3个MTU可以在较短的制造周期内完成，但是制造成本较高。

（3）MTU2的状况与 MTU5相似。最优解P＊的制造周期MT均长于预期制造任务参数Pp对应的参数，但制造成本MC与成品率MQ却低于对应的预期制造任务参数Pp对应的参数。说明制造子任务MTU2与MTU5的完成技术难度较高，需要花费较长的制造时间。

（4）预期制造任务参数Pp与最优解P＊之间存在着差距，表明盟主CMU对制造任务的属性估计不准确，对市场调研不够深入，应该结合具体的市场协作制造资源环境，针对制造任务的参数需求进行重新调整。

6 结束语

本文提出了网络环境下协同制造链的概念，对制造任务参数进行形式化描述。详细论述了协同制造链的优化构建过程、基于制造任务参数欧氏距离的优化模型以及基于自适应遗传算法的制造任务与资源的优化配置。基于制造任务参数距离模型构建的协同制造链，能够有效地扩大搜索区间，便于获得最优解。对优化结果的分析表明，协同制造链构建过程是一个制造任务与制造资源相互协调演进的过程，应该结合具体的制造任务参数和市场协作制造资源环境，不断调整才能获得最佳的任务与资源的匹配，快速、及时地响应市场的需求变化。

[1]倪中华，江勇.面向网络化制造的动态自组织制造资源模型的研究[J].中国机械工程，2004，15（20）：1823-1826.

[2]王景峰，王刚，吕民，等.基于产品结构的制造服务链构建研究[J].计算机集成制造系统，2009，15（6）：1222－1230.

[3]Davulcu H，Kifer M，Pokorny O，et al.Modelling and Analysis of Interactions in Virtual Enterprises[C]／／Proceedings of the Ninth International Workshop on Research Issues on Data Engineering.Information Technology for Virtual Enterprises.Sydney，Australia，1999：12－18.

[4]Fischer M，Jahn H，Teich T.Optimizing the Selection of Partners in Production Networks[J].Robotics and Computer－Integrated Manufacturing，2004，20：593－601.

[5]Yao C F，Zhang D H，Peng W L，et al.Research on Resources Optimization Deployment Model and Algorithm for Collaborative Manufacturing Process[J].International Journal of Production Research，2006，44（16）：3279－3301.

[6]吉锋，何卫平，王东成，等.网络制造环境下面向复杂零件的协同制造链研究[J].计算机集成制造系统－CIMS，2006，12（1）：71－76.

[7]Hwang C L，Yoon K.Multiple Attribute Decision Making[M].Berlin：Springer－Verlag，1981.