多维密度核估计的渐进正态性及稳健渐进正态性研究

张 波，刘鹤飞，陈 兴，郭洪亮

(1.云南大学 数学与统计学院昆明 650031；2.曲靖师范学院 数学与信息科学学院，云南 曲靖 655011）

0 引言

多维密度核估计的渐进正态性及稳健渐进正态性是非参数密度估计的一个非常重要的研究方向，其中非参数概率密度核估计作为非参数密度估计的重要方法，受到越来越多的学者的重视。Hardel、Miiller、Silverman、Scott等都曾致力于多维密度核估计的研究，Schuster、Singh、Susan,Walter、陈桂景、赵林成、杨振海等人得到了较好的相合速度的结果。其中Loftsgarden和Qnesenberry提出了最近邻估计，Devroye和Wagner讨论了一种窗宽依赖于样本的核估计。Gasser、Mammitzsch和Granorsky对最优核理论做了广泛的发展，Falrell、Hasminskii和Stone对核估计的最优收敛速度做了研究，Loader、Hjort和Jones研究了核函数的局部似然估计，相依数据的核密度估计的早期工作者是Roussas和Rosenblatt，他们建立了局部渐近正态性，Claeskens和Hall研究了核密度估计的MISE、ISE。虽然非参数概率密度核估计的理论主要集中在大样本上，且在应用上需要大量的数据以及复杂的运算过程，但是随着计算机技术的发展，非参数密度核估计的应用也变的越来越广泛，其应用领域逐渐涉及社会学、物理学、生物学、以及各种工程技术领域。本文将讨论多维密度核估计的渐进正态性，以及在大样本情况下的稳健渐进正态性。

1 多维密度核估计的渐进正态性

1.1 多维密度核估计的渐进正态性的定义

1.2 几个相关引理

引理1[1]若K(u)和f(X)满足条件

引理2[1]若K(u)和f(X)满足条件

引理4若K(u)和f(X)满足条件

则对于多维密度核估计，具有如下公式：

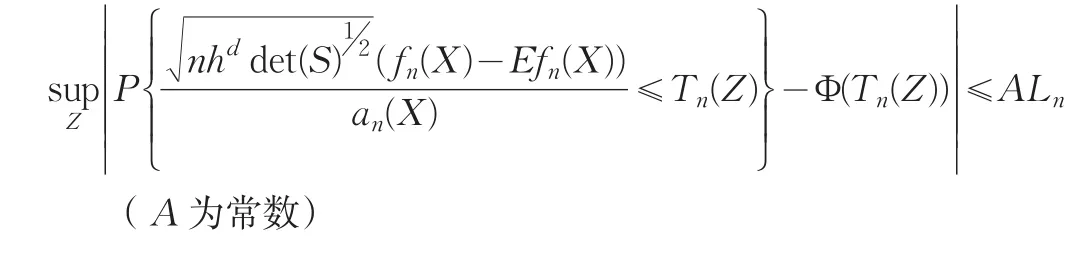
将Berry-Esseen不等式推广到n维则对于多维密度核估计有下式：

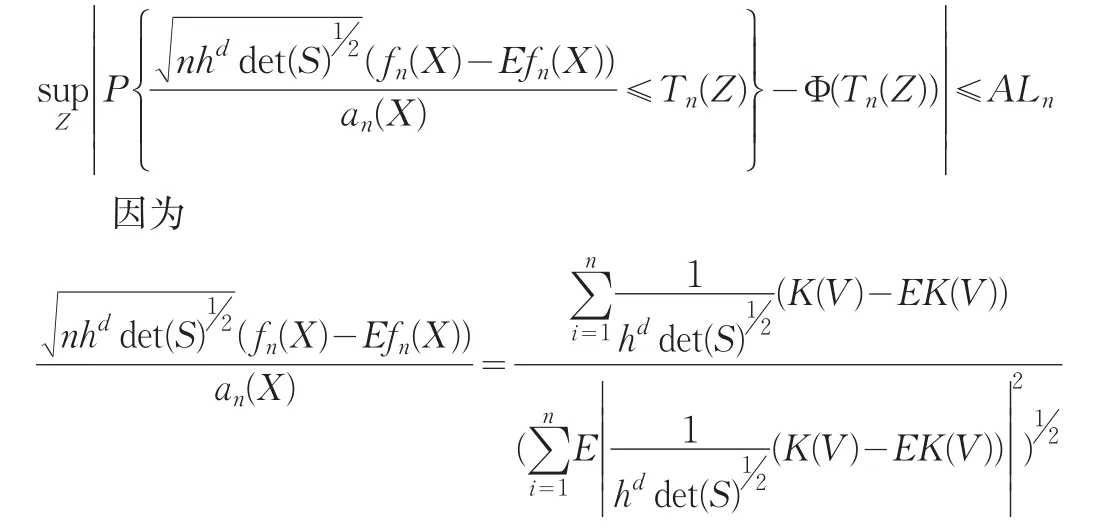
故引理得证。

1.3 多维密度核估计的渐进正态性定理及证明

定理1若K(u)和f(X)满足条件

2 多维密度核估计的稳健渐进正态性

本文将概率密度一维稳健渐进正态性的定义[3]推广到多维密度核估计中，在一定条件下我们给出多维密度核估计的稳健渐进正态性定理，并证明此定理。

定理2若K(u)和f(X)满足条件

则上式多维密度核估计是稳健渐进正态的。

证明：首先将一维概率密度核估计的均方相合性定义[1]推广到多维并应用到本文所提的多维概率密度核估计中，来证明多维密度核估计的均方相合性。即：

再利用稳健渐进正态性的定义及其在多维上的推广，并应用到多维密度核估计的稳健性渐进正态性的证明中，即

3 结语

本文基于非参数密度估计尤其是非参数密度核估计的基本原理和统计方法将以往多维密度核估计文献中的相关理论从一维推广到多维，并证明了多维密度核估计的渐进正态性和稳健渐进正态性。

[1]陈希孺.非参数统计[M].上海：上海科学技术出版社，1989.

[2]熊祖光，非参数核密度估计的空间聚类算法研究以及改进[J].吉林大学学报，2008.

[3]郑忠国.Bootstrap方法和稳健性[J].数学年刊，1986，7A(1).

[4]K.B.Athreya.Bootstrap of the Mean in the Infinite Variance Case[J].Ann Statist,1987,(15).

[5]匡继昌.常用不等式[M].济南：山东科学技术出版社，2003.

[6]B.Efron.More Efficient Bootstrap Computation[J].Ann Statist Ass,1989,(3).