复合LINEX对称损失函数下Burr分布参数的估计

李俊华

（郧阳师范高等专科学校 数学系，湖北 十堰 442000）

0 引言

Burr分布是精算师常用的八大分布之一，在社会科学、经济科学、环境科学、保险精算学等诸多领域内有着广泛的应用。所以对Burr分布性质进行深入的探讨，具有重要的现实意义，引起了越来越多的人的注意。本文将讨论复合LINEX对称损失下双参数Burr分布在参数α已知的情况下其状态参数的Bayes估计，多层Bayes估计。

考虑考虑双参数Burr分布的随机变量X，其密度函数为

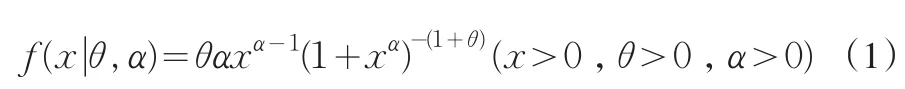
设(x1,x2,…,xn)为来自总体的i.i.d的样本，则在样本下的似然方程为

由于参数未知，人们使用各种方法对其进行估计。

1975年Varian提出了LINEX损失函数，定义为

其中，δ为参数θ的估计；a是该损失函数的尺度参数，a≠0，是一类非对称损失函数。

在文献[4]中提出了复合LINEX对称损失函数，表达形式为

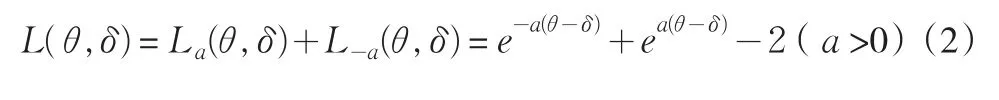
1 θ的Bayes估计

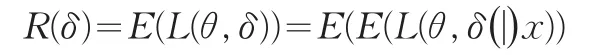
欲使R(δ)最小，只需E(L(θ,δ(|)x)几乎处处达到最小。

又因为h(δ)关于δ是严格凸函数，故δB(x)是其唯一的极小值点，进而得到Bayes估计是唯一的。

2 给定先验分布下，θ的多层Bayes估计

证明：取Γ(a,b)为θ的先验分布时，θ的后验分布为：

故在复合LINEX对称损失函数下θ的Bayes估计为

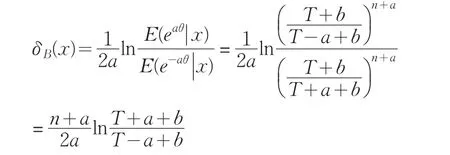
引理1在给定的Bayes决策中，对给定的先验分布π(θ)，θ的Bayes的δB(x)是唯一的，则它是容许的。

由于Burr分布可靠度估计在复合LINEX对称损失函数下是严格凸的,其Bayes估计必是唯一的，由引理可知该估计是可容许的。

在定理2中求出的参数θ的估计δB(x)中仍然含有超参数a,b，由文献[1]可知应选择a和b使得π(|λ a,b)为λ的减函数，再由Bayes估计的稳健性，可以确定超参数a和b的范围为0＜a＜1，0＜b＜c（c＞0为常数）。

若超参数a,b的先验分布为均匀分布，即π(a,b)=1/c，此时θ的多层先验密度函数为

定理3对双参数Burr分布，若θ的多层先验分布由（3）给出，则在复合LINEX对称损失函数下θ的多层Bayes证明:根据Bayes定理，θ的多层后验密度为

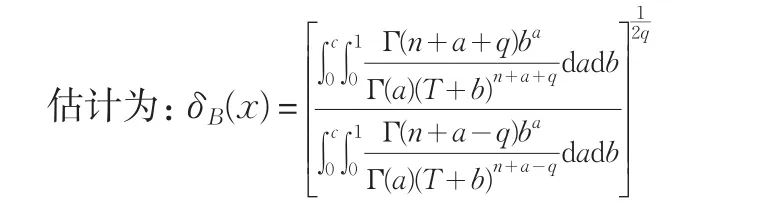
在复合LINEX对称损失函数下θ的多层Bayes估计为

[1]王学.Linex损失下Burr分布参数的Bayes估计[D].华中师范大学，2008,（5）.

[2]陈志强，韦程东，程艳霞.熵损失函数下Burr分布参数的Bayes估计[J].广西师范学院学报，2007,24（3）.

[3]韦程东，韦师，苏韩.复合LINEX对称损失下Pareto分布形状参数的E_Bayes估计及应用[J].统计与决策，2009,(17).

[4]张睿.复合LINEX损失下的参数估计[D].大连理工大学硕士学位论文，2007.