双样本尺度参数的四种非参数检验方法
2011-09-05王伏虎赵喜仓
王伏虎,赵喜仓
(江苏大学财经学院 统计系,江苏 镇江 212013)
0 引言
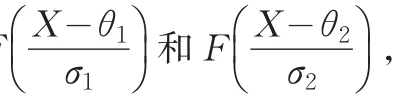
1 基本原理
使用非参数方法时,假设两个总体的位置参数θ1和θ2相等,则尺度检验的假设为

1.1 Mood检验

1.2 Ansari-Bradley检验

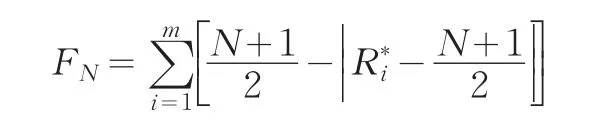
计算,见表1、2。
由于赋予极大和极小值的秩都很小,当FN的值较小,则样本X1,X2,…,Xm分布比较分散。如果FN的值较大,则样本X1,X2,…,Xm分布比较集中;对于双侧检验,给定的显著性水平α,样本容量较小时(m+n<20),可以查“Ansari-Bradley检验”表,得到临界值c1(P(FN≤c1)=1-α2)和c2(P(FN≥c2)=α2),若FN<c1或FN>c2,则拒绝原假设。当样本容量较大时,FN的渐近正态分布见表4。
1.3 Siegel-Turkey检验
将n+m个X和Y的混合样本按照大小排序,按照下表中方式重新定义混合样本中观测值的秩ai,见表3。
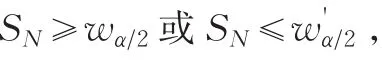
1.4 Klotz检验
在Klotz检验中,将n+m个X和Y的样本混合后按照升序排秩,然后将原始观测值的秩Ri转化为标准正态分布的Ri(N+1)分

表1 Ansari-Bradley检验中N为奇数时重新定义的秩

表3 Siegel-Turkey检验中重新定义的秩
2 实例分析
食品包装机器在包装食品时,每盒食品的平均包装量(单位:千克)必须稍微超出食品包装盒上所贴的含量,每台机器在包装食品时可能会造成不可避免的变化量,为了检验两台机器在包装食品时的变化量是否相同,测量得到如表5的数据。

表4 大样本渐近条件下4种尺度参数的非参数检验的统计量、均值和方差

表5 原始数据及计算表

表6 实例中四种检验统计量、统计量均值及方差
根据表3中计算得到的统计量,可以计算得到4种非参数检验的统计量、均值、方差及近似正态分布下的检验统计量,见表6。

3 结论
根据实例分析,可以发现4种检验方法中Ansari-Bradley检验、Siegel-Turkey检验和Klotz检验的结论一致,而Mood检验的结论和它们相反。由于实例选取的样本容量较小,在大样本情况下,这4种方法对相同数据的检验结论是一致的。
[1]W.J.Conver..实用非参数统计[M].崔恒建译.北京:人民邮电出版社,2006.
[2]王星,非参数统计[M].北京:人民大学出版社,2005.
[3]Jean Dickinson Gibbons,Subhabrata Chakraborti.Nonparametric Statistical Inference[M].New York:Marcel Dekker,inc,2003.
[4]施锡铨,范正绮.数据分析方法[M].上海:上海财经大学出版社,1997.
