尖卵形弹丸侵彻薄靶板数值模拟

2011-09-04郭秋萍焦志刚刘宗超

沈阳理工大学学报 2011年6期

郭秋萍，焦志刚，刘宗超，杨丽

(沈阳理工大学装备工程学院，辽宁沈阳110159)

现代海战中，大多数反舰导弹攻击方式为半穿甲内爆式，舰船内部结构一般设置为多层间隔靶板以保护内部设备和人员的安全，因此半穿甲弹剩余速度及靶板的破坏形式是弹丸完成作战任务的重要因素。舰船外板相对于弹丸头部长度属于金属薄板，尖头弹丸侵彻金属薄板在一定条件下发生穿甲机理较为复杂的花瓣型破坏。花瓣型破坏理论研究主要基于动量守恒［1］和能量守恒［2］，这些研究假设靶板破坏形式为单一的花瓣型，推导出弹丸的剩余速度和弹道极限。然而，实际花瓣型穿孔常伴随着几种模式同时发生，在这种破坏形式下，经验公式和理论分析具有一定局限性。本文依据某型半穿甲弹特点建立尖卵形弹丸侵彻金属薄靶的模型，运用ANSYS/LS-DYNA有限元软件进行数值模拟，分析不同情况下弹丸剩余速度及靶板破坏形式，为某型半穿甲弹丸的研制工作提供依据。

1 弹靶结构与材料模型

弹丸头部为尖卵形，尖拱曲率比CRH值为1.2，弹丸直径为7.6cm，质量 3.667kg，材料为35CrMnSiA。靶板半径为25cm，材料为装甲钢。应用LS-DYNA软件，单位制为cm-g-μs，建立弹体和靶板1/2有限元模型，选取solid164三维实体单元，采用单点积分，进行沙漏控制。计算模型使用拉格朗日网格，以映射方式划分为六面体单元(如图1所示)。弹体与靶板之间采用面-面侵蚀接触，靶板周围为固定约束，即考虑靶板边界的影响。

图1 靶系统模型

弹体和靶板材料模型均选取Johnson-Cook模型，其数学表达式为

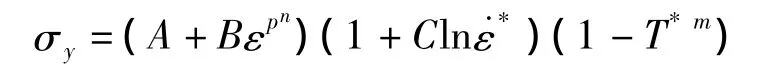
其中:εp为塑性应变;ε*=εp/ε˙0为无量纲的塑性应变率;ε˙0=1.0s-1;T*=为相似温度;Tm为材料的熔点;T0为参考温度(室温);A为静态屈服极限;B为应变硬化模量;C为应变率系数;m、n分别为热软化指数、应变硬化指数。

材料的失效判据采用最大失效塑性应变与最大静水压判据，数学表达式为

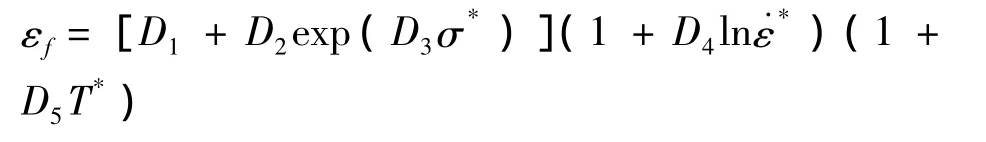
其中:σ*=p/σe;P为静水压力;σe为等效应力;D1、D2、D3、D4、D5为材料常数，由霍普金森杆实验测试得到。

材料重要参数如表1所示。

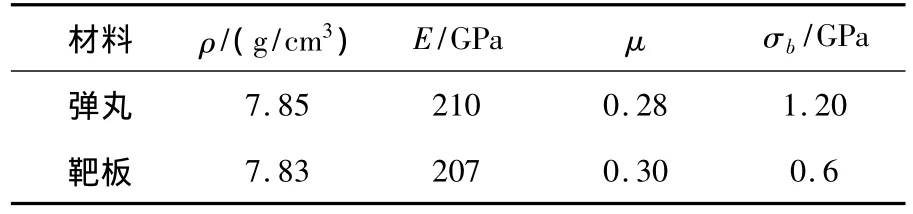
表1 弹丸、靶板材料参数

2 花瓣型破坏动量理论

尖卵形弹丸侵彻薄板发生花瓣型破坏，如图2所示。Zaid等［1］基于动量守恒原理考虑了靶板的花瓣型变形模式，认为靶板裂缝开始出现在弹尖处，当弹体前进扩大靶孔时，靶板裂缝向外发展，由于撞击很快，当弹体穿过靶板时，认为靶板内部受撞击的影响局限在半径为rA范围内，系统动量守恒定律为

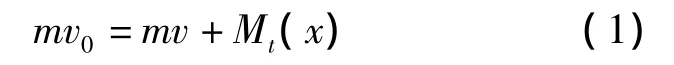
式中:m为弹丸质量;v0弹丸撞击速度;v为弹头穿过靶板后x处的弹体速度;Mt(x)为当弹头穿过靶板后至x时，靶板的动量。Mt(x)表达式为

式中:s为靶板质点在未变形前与轴线的距离;ρt、ht分别为靶板的密度和厚度;ξ为质点位移。

尖卵形弹头部尺寸几何关系(如图2所示)为

将式(3)代入式(1)、式(2)求解，可得尖卵形弹丸速度损失表达式为

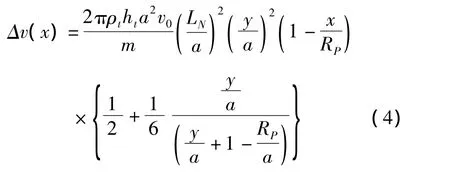
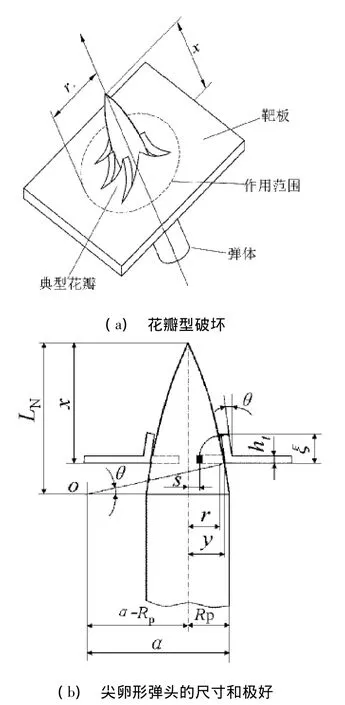
图2 花瓣型破坏模型及尖卵形弹头尺寸

3 结果分析

3.1 侵彻过程分析

弹丸以400m/s着速，侵彻1.5cm厚钢质靶板，侵彻应力云图如图3所示。弹丸在226μs时刻穿透靶板，剩余速度为359.916m/s，靶板破坏形式为花瓣型。仿真结果表明，弹丸侵彻靶板分三个阶段。第一阶段:弹丸逐渐侵入靶板，与弹尖部接触处的靶板产生屈服并出现局部隆起;第二阶段:弹丸头部扩出靶板，靶板产生盘型凹陷并受到较大的环向拉应力，出现缩颈，最终产生裂纹;第三阶段:弹丸头部穿过靶板，靶板整体塑性变形增大，径向裂纹扩大，形成花瓣，花瓣产生弯曲变形，最终飞离靶板。

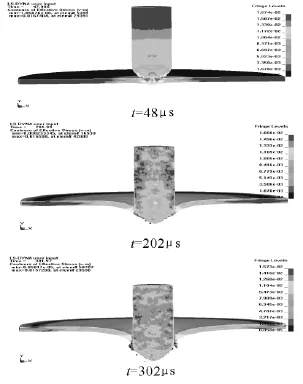
图3 侵彻应力云图

系统产生的滑移能和沙漏能随时间变化情况如图4a所示，均未超过系统内能的5%，仿真结果在可接受的范围内。弹、靶系统能量随时间变化情况如图4b所示，弹丸动能被消耗，分别转化为弹丸的内能、靶板动能和内能、侵蚀单元的动能和内能，226μs时系统各部分能量不变即侵彻结束。仿真结果表明弹丸的动能损失转化为靶板内能和动能，即靶板塑性变形能、弹性变形能、裂纹的传播和扩展以及波动效应能，其中以靶板的塑性变形能为主，包括靶板的盘型凹陷和局部隆起以及花瓣弯曲等损耗的能量［3］。

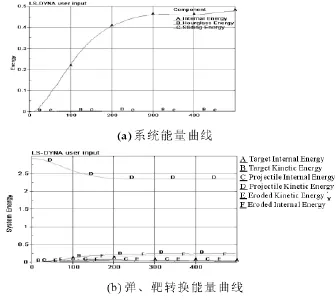
图4 能量曲线

3.2 头部形状分析

尖拱曲率比CRH为头部尖拱半径与弹丸直径的比值，为分析不同头部形状对侵彻的影响，分别对CRH为1.9、0.8、0.65弹丸以400 m/s着速侵彻1.5cm厚靶板过程进行数值模拟。CRH值为1.9，弹丸在211μs时刻穿透靶板，弹丸剩余速度为354.54m/s如图5所示，靶板破坏形式为花瓣型，如图6a所示;CRH值为0.8，弹丸在207μs时刻穿透靶板，弹丸剩余速度为360.26m/s，靶板破坏形式为花瓣型和冲塞型，如图6b所示;CRH值为0.65，弹丸在191μs穿透靶板，弹体剩余速度为361.86m/s，靶板破坏形式为冲塞型，如图6c所示。仿真结果表明CRH值增大，弹丸剩余速度降低，侵彻时间增加，靶板破坏形式由花瓣型转变为冲塞型。

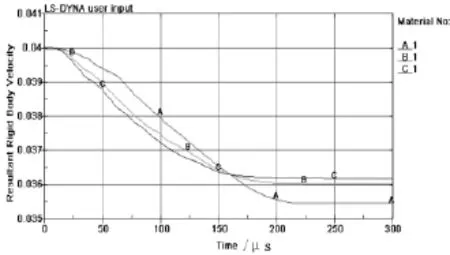
图5 不同CRH弹丸值剩余速度曲线

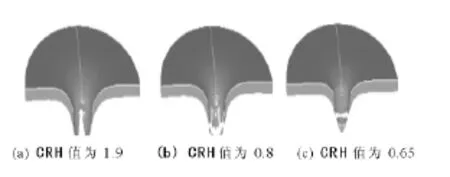
图6 不同CRH值靶板破坏形式

3.3 着速分析

当弹丸以400～800m/s着速侵彻1.5cm厚靶板时，弹丸剩余速度如表2所示。着速为800m/s，弹丸在100μs时刻穿透靶板，弹丸受到最大过载值为52698g(图7)，靶板产生较小的局部隆起，无盘型凹陷，孔洞边缘平整，靶板的最终破坏形式为花瓣型，花瓣最终飞离靶板(图8)。结果表明随着弹丸速度的增大，弹丸所受过载值增大，靶板的塑性变形减小，靶板最终的破坏形式均为花瓣型。

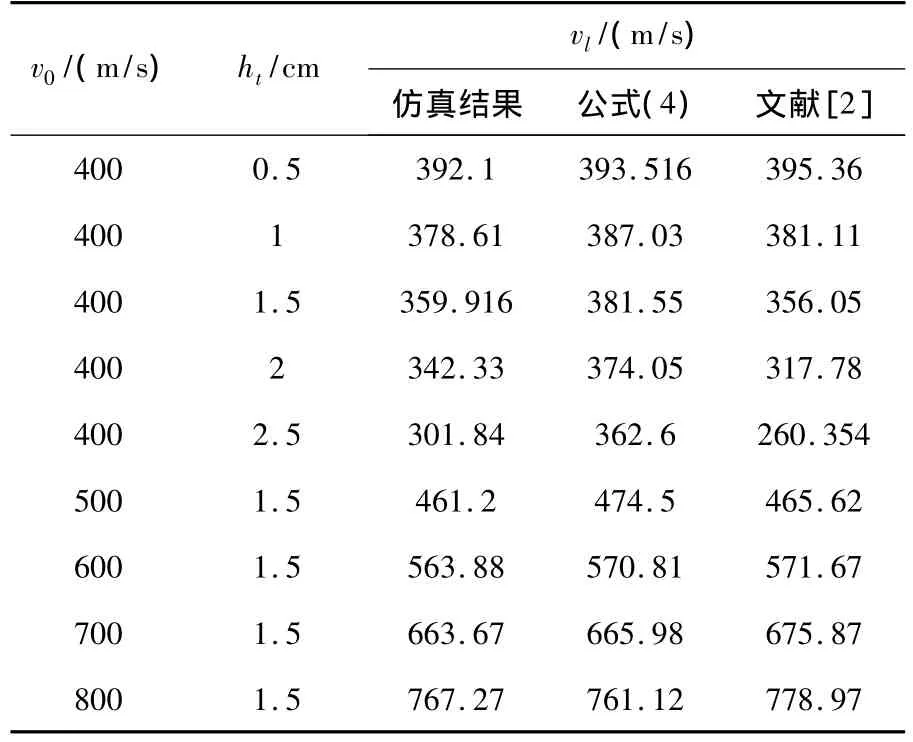
表2 弹体剩余速度值

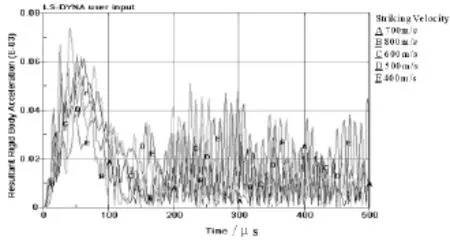
图7 不同着速下过载曲线

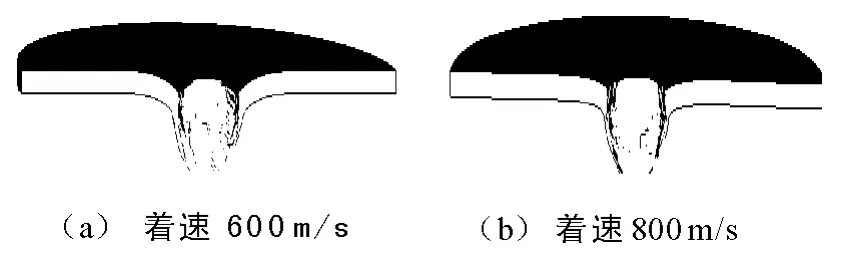
图8 不着速时靶板破坏形式

3.4 靶厚分析

当弹丸以400m/s着速侵彻0.5～2.5cm厚度的靶板时，弹丸剩余速度如表2所示。弹丸侵彻0.5cm厚度靶板，在178μs穿透靶板，弹丸剩余速度为392.1 m/s，最大过载值为10644g(如图9所示)，靶板产生较大的塑性变形，破坏形式为花瓣型和冲塞型，花瓣保持完好，如图10所示;弹丸侵彻1～2cm厚度靶板，靶板产生局部隆起与盘型凹陷，破坏形式为单一的花瓣型;弹丸侵彻2.5cm厚度靶板，在364μs时刻穿过靶板，剩余速度为300 m/s，最大过载值为85851g，靶板破坏形式为韧性扩孔和花瓣型，花瓣最终飞离靶板。结果表明，随着靶板厚度的增加，弹丸剩余速度降低，侵彻时间增长，弹丸受到的最大过载值增大，靶板的破坏形式由花瓣和冲塞型到单一的花瓣型再到韧性扩孔伴随着花瓣型。

图9 不同靶厚时弹丸过载曲线

图10 不同靶枝厚度时靶板破坏形式

4 仿真结果与理论计算对比

分别按公式(4)和文献［2］中的理论公式进行计算，靶板断裂应力取700MPa，得到理论计算结果与仿真结果对比值，如表2所示。弹丸着速为500～800m/s，公式(4)计算结果与仿真结果相吻合，低速范围内计算误差较大，原因是该公式忽略了靶板内部的应力束缚，弹丸在低速区撞击靶板时，塑性功占主导地位，结论与文献［1］吻合。靶板厚度为2.5cm时根据文献［2］中理论公式计算得到结果误差较大，原因是靶板破坏形式不是单一的花瓣型。