子母弹子弹落点散布模拟仿真

闫思江，乔相信，万仁毅

(1.青岛港湾职业技术学院机械系，山东青岛246604;2.沈阳理工大学装备工程学院，辽宁沈阳110159)

子母弹能大幅度提高炮兵的战斗力，其优越性表现为具有较高的瞬间火力密集度和较大的覆盖范围［1］，在一定程度上弥补了火炮弹药精确度不高的缺陷。子母弹子弹落点散布规律是影响其毁伤效能的重要因素，是火力运用方案制定和作战决策的依据。通常采用的方法是通过建立子母弹弹道模型，计算子弹弹道和落点散布，获得子母弹抛撒半径及母弹抛撒高度。因此，研究子母弹子弹散布规律的计算方法十分重要。基于Matlab的子弹落点散布仿真是实现这一目标的途径之一。

1 子弹落点散布统计计算模型

1.1 子弹落点散布中心计算

设子弹的落点坐标为(x1，z1)，(x2，z2)，……，(xn，zn)(n为子弹总数)，散布中心坐标为

1.2 子弹落点散布计算

根据子母弹弹道特性，当子弹落点散布为椭圆时的椭圆方程为

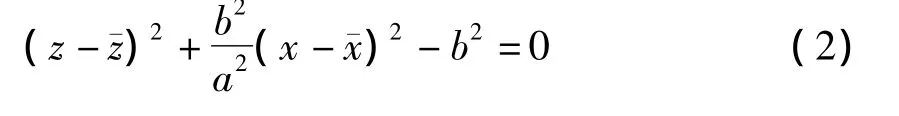
令:

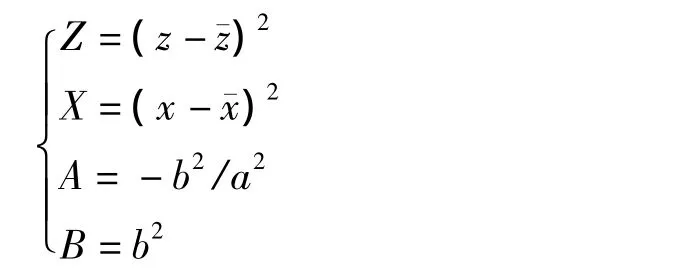
则式(2)变为

设:

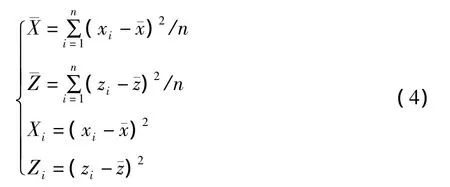
根据最小二乘法有

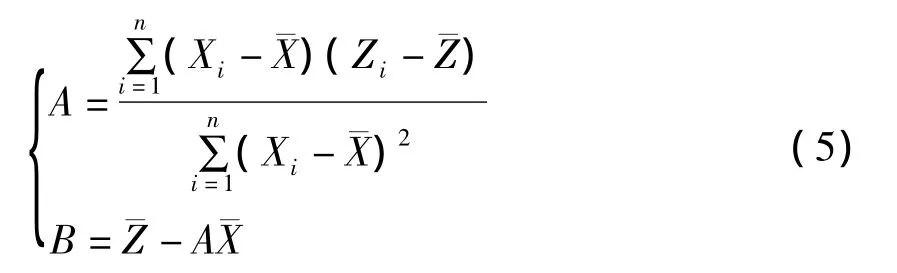
所以椭圆的长、短半轴分别为

2 子弹飞行外弹道计算

2.1 坐标系的建立

为描述子弹运动，建立三个坐标系［2］，其位置如图1所示。地面坐标系O-XYZ固连于地面，其中OX轴平行于水平面，指向射向，原点O为抛射时刻母弹的质心P点在地面的投影点。平动坐标系O1-X1Y1Z1的各轴平行于地面坐标系，O1为抛撒时刻母弹的质心。速度坐标系O2-X2Y2Z2与平动坐标系的原点重合，该坐标系由平动坐标系绕O1Z1轴顺时针旋转θ角得到，θ角是弹道倾角，O1X2轴与母弹飞行速度方向一致。

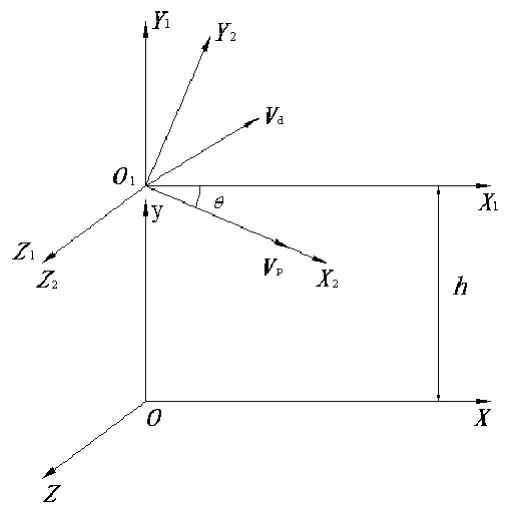
图1 子弹运动坐标系

2.2 子弹初始状态顺时针旋转

或

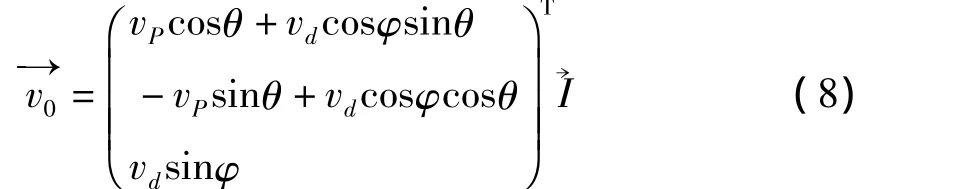
2.3 子弹运动方程［3］

［2］的阻力随高度变化关系

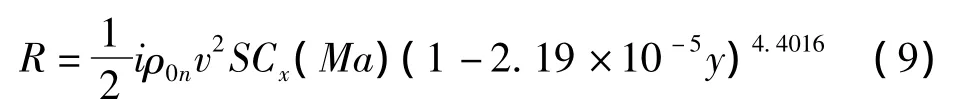
式中:ρ0n为地面空气密度，其值为1.206 kg/m3;S为子弹横截面积;Cx(Ma)为子弹随马赫数变化的阻力系数。

子弹运动方程为

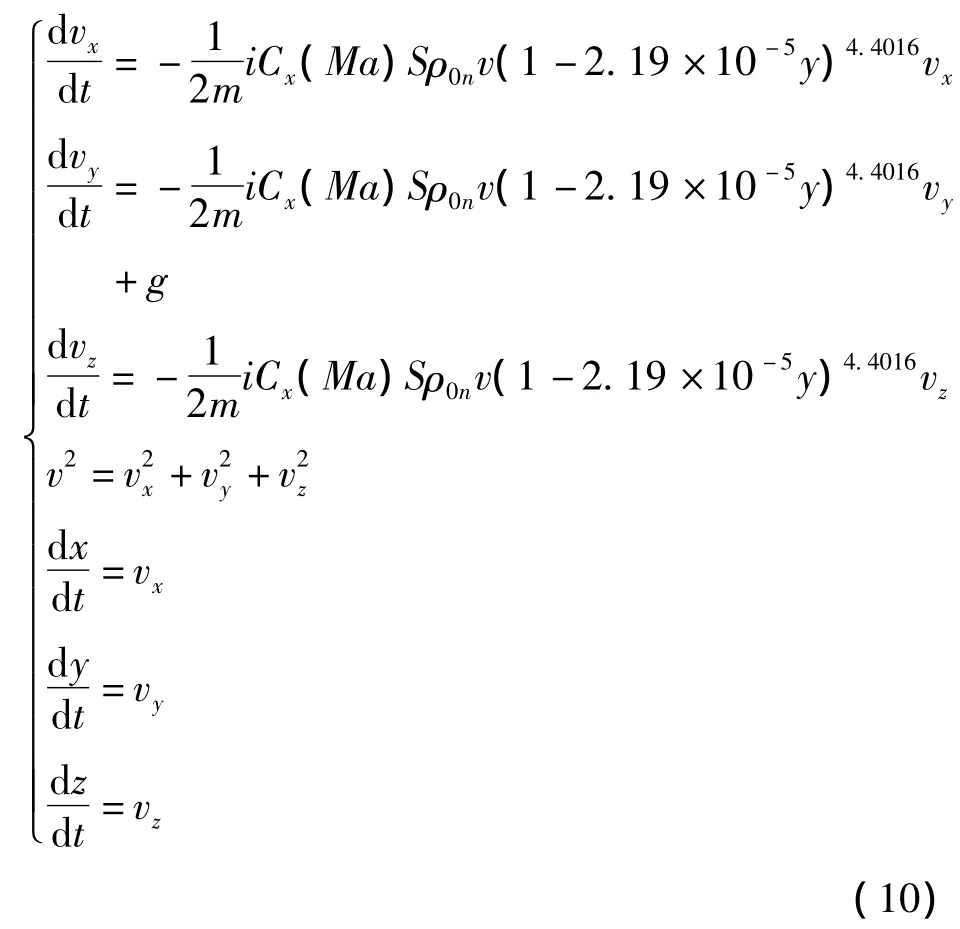
式中，m为子弹质量，g为重力加速度，取9.8m/s2。

在地面坐标系中，初始条件为x0=z0=0，y0=h，t0=0，终止条件为 y=0。

3 参数确定及计算实例

计算方程中的参数由子母弹的结构和母弹弹道决定［4］，φ角是质心在y2轴左边的第一枚子弹圆心与y2轴正向夹角，取值范围是［0，2π /N］(N为一圈子弹的个数)。按逆时针对子弹进行编号，质心在y2轴左端第一枚子弹为1号，依次为2、3、4、5，如图2所示。相邻两枚子弹夹角为

第ni枚子弹与y2轴正夹角为

计算条件为 N=5，m=0.231kg，i=1.0，Cx(Ma)=0.365，子弹直径为 0.0392 m，ρ0n=1.206 kg/m3，φ 分 别 为 36°，180°，324°。vP=307.56m/s，vd=53.02 m/s，母弹弹道倾角为 60°。

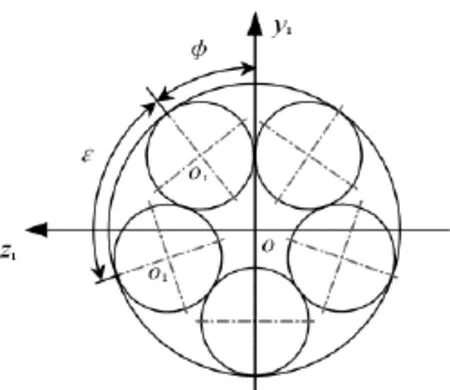
图2 子弹端面运动坐标系

4 Matlab/Simulink仿真

运用Simulink进行子弹飞行外弹道仿真，求出子弹落点在X轴和Z轴方向上的距离及子弹下落飞行时间。

4.1 Simulink模块简介

基于Matlab的子母弹子弹落点散布Simulink模拟仿真模块如图3所示。

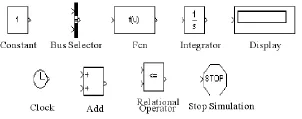
图3 Simulink常用模块

表2 模块功能

4.2 Simulink仿真模型

Simulink仿真模型如图4所示(见下页)。

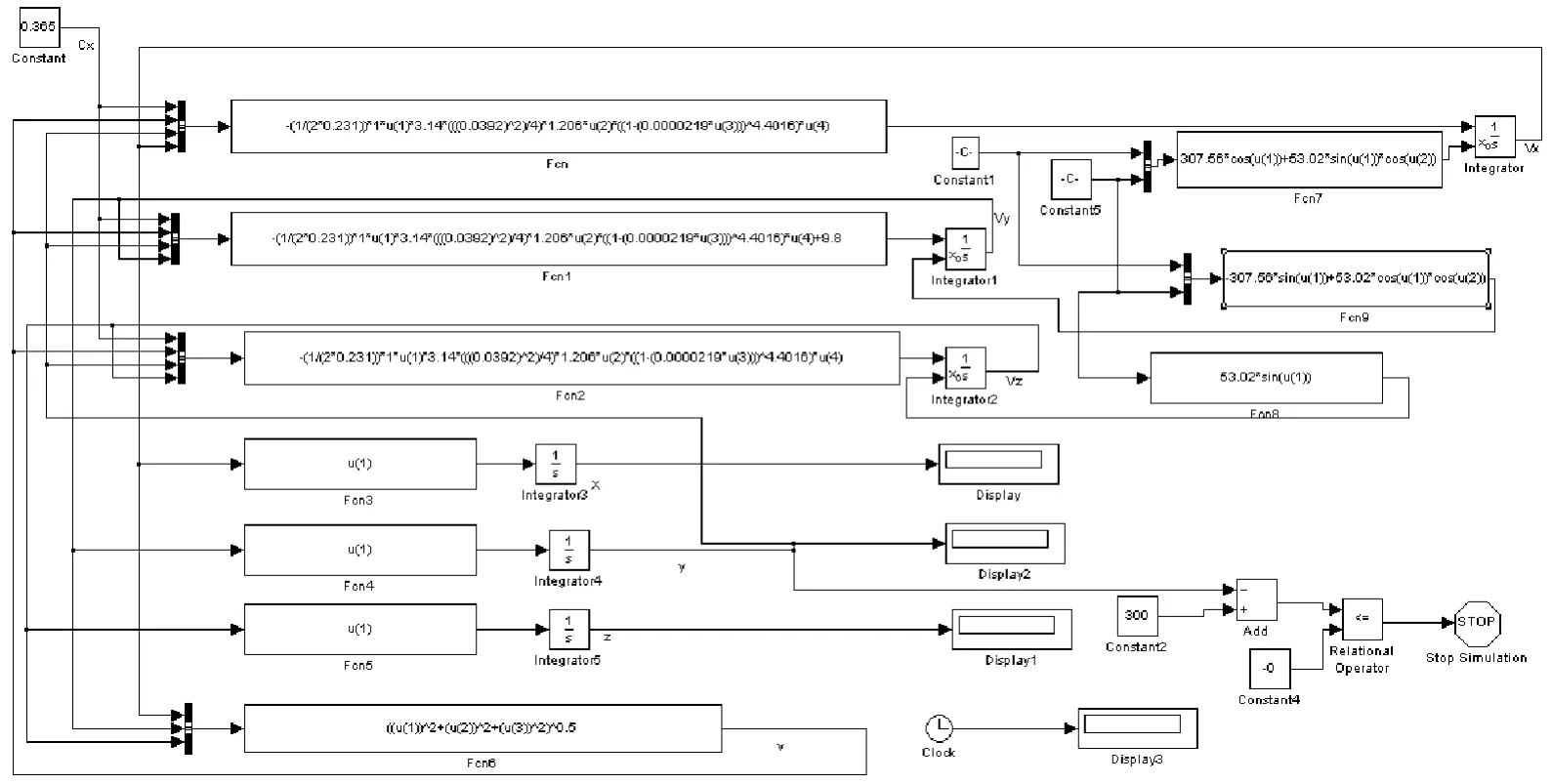
图4 Simulink仿真模型

4.3 仿真结果输出及分析

通过Matlab/simulink求解子弹运动方程，结果输出见图5、图6和图7。

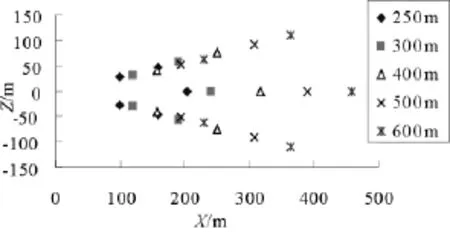
图5 子弹抛撒高度对散布的影响

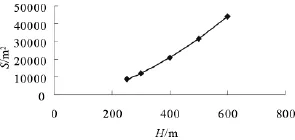
图6 子弹散布面积随抛撒高度的变化

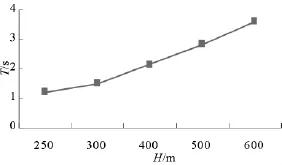
图7 子弹下落时间随抛撒高度的变化

由仿真结果看出:随着母弹抛撒高度增大，子弹落点散布半径、下落时间随之增大。在同一层上的五枚子弹，在地面形成的图形近似椭圆，椭圆的面积随抛撒高度升高而增大;同层子弹的下落时间不同，这是由于子弹从母弹中抛出的速度不同;子弹在地面散布所形成的椭圆关于X轴对称，在φ为180°的子弹落点最远。

5 结论

通过计算和建立Matlab/Simulink模拟仿真模型，实例模拟结果证明，利用Matlab软件能够准确模拟计算出子母弹飞行外弹道和落点散布，且与前人的理论计算和分析及试验结果具有较好的一致性。Matlab软件能使仿真结果更直观，更能提高计算效率，从而在子母弹外弹道计算时达到事半功倍的效果。

参考文献:

［1］孔维红，姜春兰，王在成.某型航空子母弹子弹地面散布研究［J］.航空兵器，2005，(4):43-46.

［2］李军营，张毅，马清华.弹道导弹子母弹落点散布分析［J］.飞行力学，2003，21(2):45-47.

［3］房玉军，蒋建伟.子弹药抛撒随机外弹道模型及蒙特卡洛解法［J］.北京理工大学学报，2009，29(10):850-853.

［4］游宁，马宝华.火炮子母弹抛撒段子弹运动规律初探［J］.兵工学报，1997，18(4):302-307.