灌溉用聚乙烯管道抢修节结构优化研究

余 龙，俞树荣，桂 芳，杨尚军

(1.兰州理工大学石油化工学院，甘肃兰州730050;2.兰州威立雅水务(集团)有限责任公司，甘肃兰州730050)

随着农业科技化的程度逐渐提高，农业耕种对灌溉用水的需求也越来越大。聚乙烯管道具有重量轻、耐腐蚀、管壁光滑、过流能力大、密封性能好、使用寿命长、运输安装方便及施工速度快等良好的使用性能，在农用埋地供水管网中开始广泛应用。聚乙烯属于柔性管材，与刚性管材相比，柔性管材刚性较小，敷设深度更大，因此聚乙烯供水管道破裂后抢修难度较大。

抢修节是聚乙烯供水管道堵漏抢修最有效的设备，但现有抢修节对于聚乙烯管道变形所导致的二次泄漏问题却未能根本解决。本文结合兰州威立雅水务(集团)有限责任公司开发的新结构聚乙烯管道抢修节，通过有限元计算得到聚乙烯管道抢修节密封位置的位移量，以减小最大位移量、提高密封比压作为优化目标，选取重点结构参数进行迭代运算，找到对密封性能影响较大的参数进行结构优化。

1 聚乙烯供水管抢修节泄漏的原因

聚乙烯供水管破裂后，经常会发生抢修节安装后依然泄漏的现象。导致抢修节堵漏失败的原因较多，与管道破裂情况、现场环境、施工安装以及管道与抢修节的变形不协调等因素均有关系。其中管道与抢修节变形不协调导致泄漏的现象较多，也较难处理，因此需要有针对性地进行分析和探讨。

在保障抢修节强度满足设计要求的前提下，对于由变形导致泄漏的情况，主要有两个原因:

(1)聚乙烯供水管道变形

灌溉用聚乙烯供水管道通径一般均超过300mm，管道结构刚度与管周土体刚度的比值αs＜1，因此属于柔性管道。聚乙烯管道的刚度相对较小，在静水压力以及自重的作用下，聚乙烯管道径向会发生变形。按照中国工程建设标准化协会标准《埋地聚乙烯(PE)供水管管道工程技术规程》之规定，在同样施工条件下，柔性管道敷设深度应为刚性管道的3～4倍，但具体施工中很难达到。

当破裂聚乙烯管道安装抢修节后，管道破裂位置的内外壁均充满水介质，使得管壁内外侧的压力相同，导致该位置缺少水压支撑，局部位置刚度减小，聚乙烯管道与抢修节的间隙增大发生泄漏。

(2)抢修设备变形

抢修节一般为碳钢材料，其刚度比聚乙烯管道高，但由于供水压力、螺栓预紧力以及聚乙烯管道的支撑力等因素共同作用，使得抢修节在密封面局部位置产生变形量过大，一旦密封比压低于必须比压则密封失效。实际工程中由抢修节受压变形导致的泄漏，是引起聚乙烯管道堵漏失败的主要原因。

改变抢修节某些参数并不能完全达到改善密封效果的目的，甚至有时会加剧泄漏，因此需要有针对性地进行分析研究。在众多的结构尺寸中合理选择和调整，才能有效止漏。

2 聚乙烯管道抢修节优化

研究聚乙烯供水管抢修节变形泄漏，可以借助有限元分析和结构优化方法。通过有限元分析抢修节密封位置的变形情况，并以减小变形量作为优化目标，对抢修节密封结构进行优化分析，找出合理密封的结构尺寸或变化规律，最终达到提高聚乙烯供水管抢修节密封性能的目的。

优化设计是一种寻找确定最优设计方案的技术。针对多目标优化问题，可以对要优化结构计算结果进行参数化处理，绘制设计空间，快速得到多项指标皆趋向于最好的设计方案［1］。

通过有限元法将每次重分析的结果传递给选择的优化目标，作为一个新的设计参数进行数据传递，根据规定格式进行寻优计算，通过反复迭代运算后，直至达到收敛条件获得最优解。有限元法在优化过程中可通过程序控制发散域，迭代逼近目标值得到合理精度的求解［2］。

2.1 建立优化初始环境

由于聚乙烯管道抢修节结构优化属于约束优化问题，因此可利用间接解法，将目标函数去约束化，以简化问题。对于本约束优化问题，可表示为

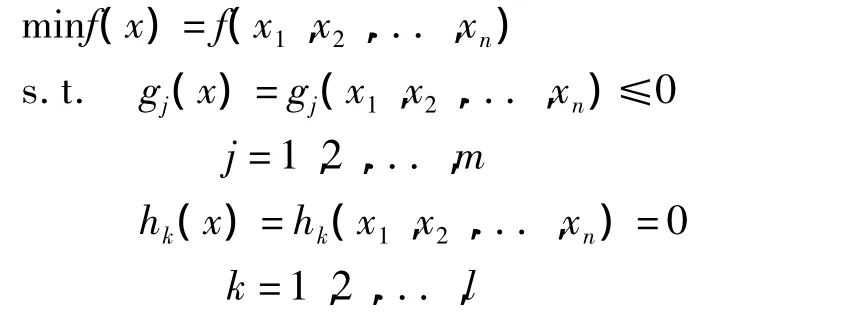
式中:f(x)为优化目标函数;x1，x2，...，xn为设计变量;n为设计变量数量;gj(x)为不等式约束条件;m为不等式约束条件数量;hk(x)等式约束条件;l为等式约束条件数量。

与聚乙烯管道抢修节实际结构相比，分析模型进行了一定的简化。对于一些不影响结果的特征，在建模过程中合理简化能够保证运算精度和速度［3-4］。根据施工情况，管道材料为聚乙烯材料，抢修节材料为Q235A，由于模拟管道破裂抢修工况，因此管道内部和抢修节内部均有水压载荷，取供水压力上限值1.6MPa施加并进行计算。

经过有限元分析，聚乙烯供水管抢修节的总变形量如图1所示，为了便于观察聚乙烯管道抢修节变型趋势，将聚乙烯管道隐去，抢修节变形趋势放大180倍。

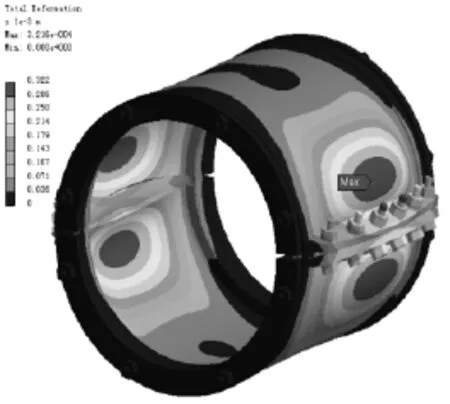
图1 聚乙烯管道抢修节变形量分布图

从图中可以看出，最大变形量为0.3216mm，在PE供水管抢修节靠近连接平台的中间位置对称分布，也因为变形量相对较大并有螺栓连接限制，所以该位置的应力值相对较大。由于聚乙烯供水管抢修节为两个半圆节并由螺栓连接，因此连接位置的变形量也较大，从管道的轴线方向进行观察，连接位置的变形使得聚乙烯供水管抢修节直边连接处有向两侧延展的趋势。

2.2 确定目标函数

聚乙烯管道抢修节结构优化的目的是减小密封面的局部变形量，使得变形协调，密封圈能够均匀回弹，使密封面密封比压稳定。首先需要通过有限元计算得到最初解，即密封面的变形量分布情况，以减小密封面变形量的最大值为目标函数，设置几个对密封性能相关度较高的结构参数作为设计变量，并设定结构参数的取值范围作为约束条件，令结构参数在取值范围内变换多次迭代运算，最终找到最优解，即可能产生密封面变形最小的结构参数，或者找到结构参数对目标函数的影响关系。

如图2所示，图中显示的是密封面法线方向上的位移量，可达0.255mm。根据抢修节的应力分布以及变形情况，结合抢修节的结构特点对特征参数进行优化。从变形图上可以看出，抢修节两侧的中间位置变形量较大，影响该位置的密封效果。

图2 聚乙烯管道抢修节密封面法向变形分布图

导致抢修节两侧中间位置变形量较大的原因是:抢修节左右两端有法兰与螺栓连接，对抢修节左右两端有固支;而抢修节两侧的中间位置只有螺栓连接，另外长度相对较大，故在该位置形成弯曲，导致变形量较大。因此选择密封面法线方向最大位移，即坐标密封面法向位移作为优化的目标函数。

2.3 确定设计变量

设计变量指在分析优化过程中可以独立改变的基本参数。抢修节上的每个尺寸参数均可作为设计变量，但由于抢修节结构尺寸较多，不可能对每个参数优化，因此需从中选取可能对抢修节的密封性能影响较大的参数。根据图2中目标位置的法向位移扰动的程度，选取翼边宽度L12、中心螺孔间距L8、螺孔开孔宽度V1以及翼边厚度FD1四个结构参数，作为优化过程中的设计变量，分布位置如图3所示(见下页)。

2.4 确定约束条件

针对聚乙烯管道抢修节密封面法向变形求极值时限制为约束条件Ω。每个设计变量在优化分析的过程中，需要有取值变化范围，作为参数的约束条件。本分析中的约束条件主要以设计变量初值10%上下范围内浮动，一些设计变量约束条件更具体，故数值变化范围更小，如翼边厚度FD1。

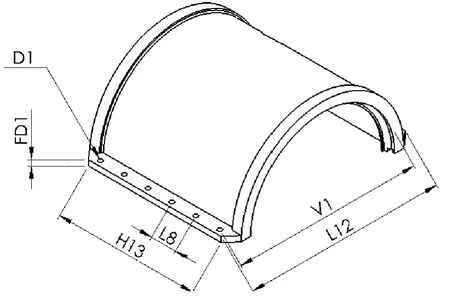
图3 聚乙烯管道抢修节设计变量分布位置图

每个参数的变换都会导致分析结果的变化，即密封面法向变形量分布的变化。同时改变多个参数，会使分析结果的样本数量迅速增加。样本数量增加能够提高计算精度，同时也导致运算量增大，延长计算分析时间。因此需要合理选择迭代次数，同时保证精度和运算时间。

按照迭代公式进行多次运算，直到求出满足准则方程的设计变量后，终止迭代运算。迭代公式如下:

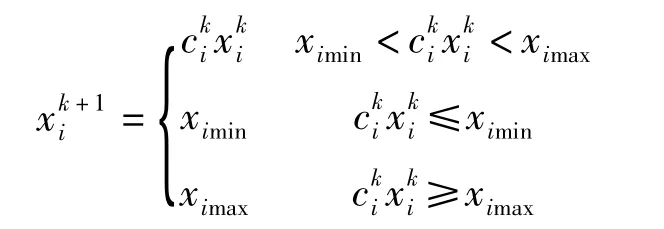
式中:xi为设计变量;ci为迭代乘子;k为迭代次数;ximin为设计变量下限;ximax为设计变量上限。

从上式可以看出，约束条件 Ω∈［ximin，ximax］。

本分析中各参数的迭代方向表示，在允许结构条件下，设计变量以及目标函数数值所期望的变化趋势，分别为Mean(平均值)、Max(最大值)和Min(最小值)，迭代运算次数为15次。设计变量与目标函数对应关系，如表1所示。

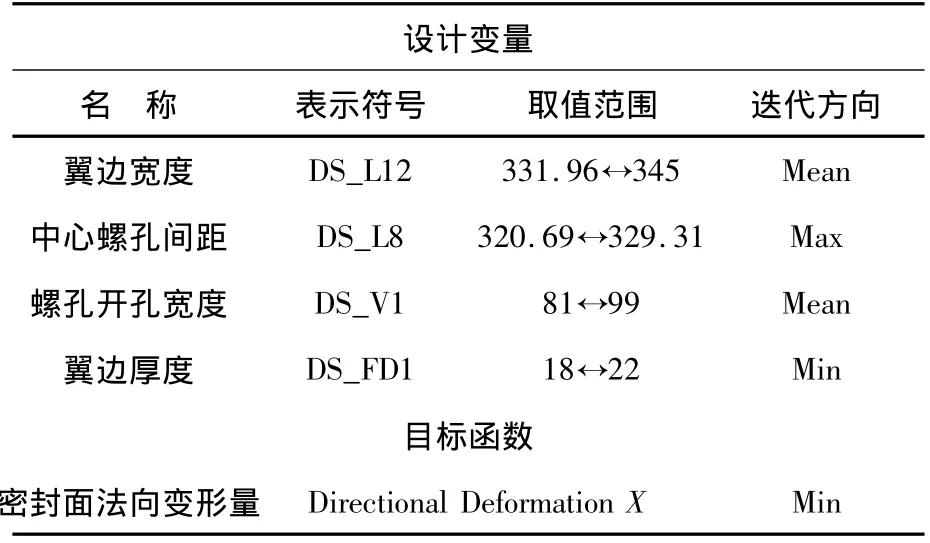
表1 设计变量与目标函数表

2.5 优化结果

通过优化迭代，找出四个结构参数在取值范围内变化时，与密封面法线方向变形量的对应关系，并生成三维响应图，云图由各对应关系的点域构成。

螺孔开孔宽度V1、翼边厚度FD1与密封面法向变形量的对应关系响应图如图4所示。

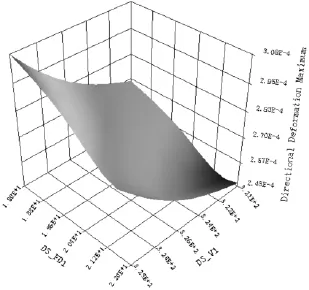
图4 FD1、V1与密封面法向变形三维响应图

螺孔开孔宽度V1越小，密封面法向变形量也越小;随着翼边厚度FD1的增大，密封面法向变形量减小，但在翼边厚度FD1为21.5mm时，密封面法向变形量最小。

中心螺孔间距L8、翼边厚度FD1与密封面法向变形量的对应关系响应图如图5所示。

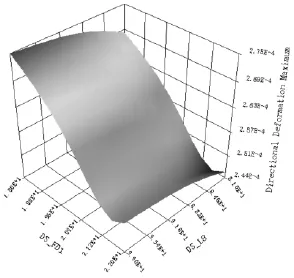
图5 L8、FD1与密封面法向变形三维响应图

随着中心螺孔间距L8的逐渐增大，密封面法向变形量也相应变大，但由于L8的取值变换范围较小，故形成的曲面斜率较小。

中心螺孔间距L8、翼边宽度L12与密封面法向变形量的对应关系响应图如图6所示。

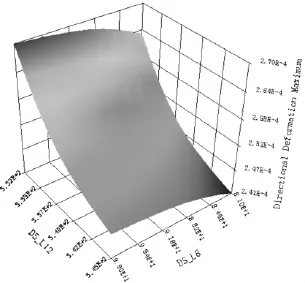
图6 L8、L12与密封面法向变形三维响应图

在取值范围内，随着翼边宽度L12增大，密封面法向变形量减小，但当翼边宽度L12增大到338mm后，增大翼边宽度L12的值，对密封面法向变形量的影响可忽略不计。

3 设计变量敏度分析

结构敏度分析是通过改变结构参数，将各参数的扰动对系统响应的影响程度进行评估的方法，是结构优化的重要基础［5］。对设计变量进行敏度分析的目的，是判断这些参数对密封性能影响程度的大小，找到对密封性能影响较大的参数。

得出设计变量与目标函数的关系，还需要确定这些参数对密封面法向位移的影响程度的大小，施工过程中可优先考虑对密封面法向位移影响较大的结构参数，对于影响较小的结构参数根据具体情况可以忽略。在敏度计算过程中，目标函数与约束条件均以一阶泰勒显示化表示，通过有限元迭代运算逼近收敛区域，得出目标函数对结构参数设计变量的响应敏度［6］。

根据位移型泛函敏度计算公式，抢修节密封面分布上的密封比压与应力相对应，可得到响应敏度 δψk，即可表达为［7］

式中:Γ为接触边界;φ为应力约束条件;n为外法线向量;V为设计速度场;σij()为应力张量;εij()为应变张量。

结合结构敏度分析，可合理选取与聚乙烯管道抢修节密封结构有关的主要参数，作为分析的设计参数，从中找出对聚乙烯管道抢修节密封性能影响较大的参数，得到导致聚乙烯管道抢修节密封失效的主要因素以及解决方案。由此得出结构参数对密封面法向位移的敏度响应图，如图7所示。

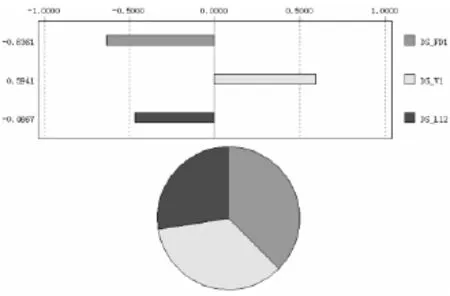
图7 结构参数敏度响应图

根据对聚乙烯管道抢修节结构优化结果，四个设计变量的变化规律如下:

(1)翼边宽度L12取值范围可在332～345mm之间，但翼边宽度过小会导致密封面间隙增大，翼边宽度达到338mm即可，再增大翼边宽度对密封效果影响不大。翼边宽度L12对密封面位移敏感度影响为-0.4667。

(2)螺孔开孔宽度V1取值范围可在321～329mm之间，螺孔开孔宽度越大密封面间隙也会越大。螺孔开孔宽度V1对密封面位移敏感度影响为0.5941。

(3)翼边厚度FD1取值范围可在18～22mm之间，翼边厚度增大密封面间隙会减小，翼边最佳厚度为21.5mm。翼边厚度FD1对密封面位移敏感度影响为-0.6361，因此在四个参数中翼边厚度影响对密封面位移最大。在实际施工中，如增大翼边厚度有困难，可考虑加筋。

(4)中心螺孔间距L8对密封面位移敏感度影响为0.075941，因此它的变动对密封面位移的影响可以忽略不计。

4 结论

兰州威立雅水务(集团)有限责任公司于2007年开始向榆中和平乡供水，共铺设Ф600mm聚乙烯供水管65公里，流速平均为1.2m/s。于当年采用兰州威立雅水务(集团)有限责任公司研发的新型聚乙烯管道抢修节，密封堵漏效果显著，共计34次维修记录中，未出现二次泄漏情况。本设备对使用聚乙烯供水管道节水灌溉应用，具有一定实用价值。

1)从抢修节有限元分析结果可以看出，在1.6MPa供水压力下，抢修节最大变形量为0.3216 mm，分布位置在抢修节靠近密封面的中间位置，对密封效果产生影响。

2)结构尺寸变化趋势对密封效果有影响。翼边宽度增大，螺孔开孔宽度减小、翼边厚度增大均能减小密封面法向位移，提高密封效果。

3)通过结构尺寸的敏度分析，找到对密封性能影响较大的结构尺寸，忽略对密封性能影响较小的参数，调整高敏度尺寸可明显改善密封效果，进而提高抢修效率。翼边宽度、螺孔开孔宽度和翼边厚度对密封效果影响较大，中心螺孔间距对密封的影响可忽略不计，故该参数可依据具体工艺确定，可调整性增大。

［1］李兵，何正嘉，陈雪峰.ANSYS Workbench设计、仿真与优化［M］.北京:清华大学出版社，2008.

［2］Alessandri C，Tralli A.Sensitivity analysis for unilateral contact problems:boundary variational formulations and BEM discretizations［J］.Comput Mech，2005，(15):287-300.

［3］胡海峰.基于实体的有限元建模技术［J］.机械，2003，30(5):78-80.

［4］王鹰宇，姚进，成善宝.基于ANSYS环境的参数化有限元建模［J］. 机械，2003，30(4):12-14.

［5］A.Tafreshi.Shape sensitivity analysis of composites in contact using the boundary element method［J］.Engineering Analysis with Boundary Elements，2009，(33):215-224.

［6］余龙，俞树荣.基于敏度分析的三偏心蝶阀密封特性研究［J］.化工机械，2010，37(4):428-432.

［7］孙靖民，梁迎春，陈时绵.机械结构优化设计［M］.哈尔滨:哈尔滨工业大学出版社，2004.