基于坐标变换的制导炮弹攻角侧滑角观测器

杨荣军，王良明，杨 桦

（1.南京理工大学能源与动力工程学院，江苏 南京 210094；2.中国北方工业公司，北京 100053）

0 引言

为提高制导炮弹的控制精度，近年来国内外相关学者将反馈线性化、状态依赖Riccati方程和滑模控制等非线性理论应用于飞行控制系统设计中，取得了较好的效果［1－3］。值得注意的是，这些高性能飞行控制系统需要反馈更多的系统状态变量信息。然而实际中受弹体空间、造价等条件的限制，制导炮弹的弹载测量设备有限，在应用非线性控制方法时所需的攻角、侧滑角等状态量是不易直接精确测量的，这样很自然地就提出了制导炮弹系统的状态观测（或状态重构）问题［4］。目前非线性系统的状态观测器设计还没有系统的方法，文献［5］利用输入输出线性化理论研究了非线性系统的拓展龙伯格观测器；文献［6］设计了基于高超声速飞行器纵向动力学模型的滑模观测器，但是制导炮弹纵向和侧向的耦合特性使得构造合适的滑模面较为困难；文献［7］提出了一种适用于具有分块矩阵形式多输入多输出系统的高增益观测器，而该方法要求系统具有严格的反馈形式，且繁琐的设计过程难以实际运用。为此，本文提出一种基于坐标变换的制导炮弹攻角、侧滑角观测器。

1 非线性系统坐标变换方法

制导炮弹是一个复杂的多输入多输出耦合的非线性系统，在观测器设计时难以运用常规的线性理论。微分几何理论的发展为处理该类问题提供了有效的方法，通过合适的非线性坐标变换，可以实现系统的精确线性化。

设状态向量x∈Rn，控制输入向量u∈Rm，输出向量y∈Rm，f、h为光滑向量场，考虑如下形式的m输入m输出非线性系统

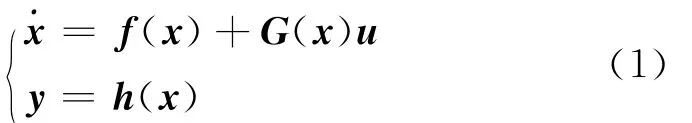
若系统的相对阶ρ1，…，ρm满足存在零动态，定义坐标变换向量

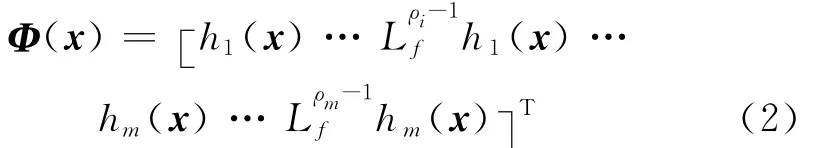
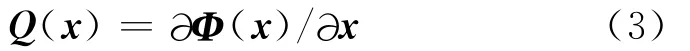
非奇异，则Φ（x）是系统的一个微分同胚，即可由式（2）的坐标变换将原系统等价转化成如下解耦的线性系统：

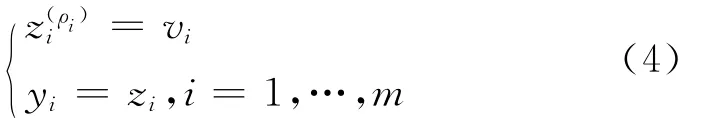
2 制导炮弹攻角侧滑角观测器

由于实际测量条件的限制，制导炮弹在应用先进的非线性控制方法时所需的攻角、侧滑角等状态是不易直接精确测量的，本文提出了一种基于坐标变换的状态观测器来估计飞行中的攻角与侧滑角姿态。该观测器采用了降阶的系统模型，针对该模型存在的非线性耦合问题，采用了坐标变换方法将其转化为解耦的线性系统，进而参考线性系统理论构造了利用角速度、加速度信息的攻角、侧滑角观测器，其增益矩阵可按期望的误差动态性能进行配置。

2.1 制导炮弹攻角、侧滑角观测系统模型

由制导炮弹角速度向量的转动关系可得

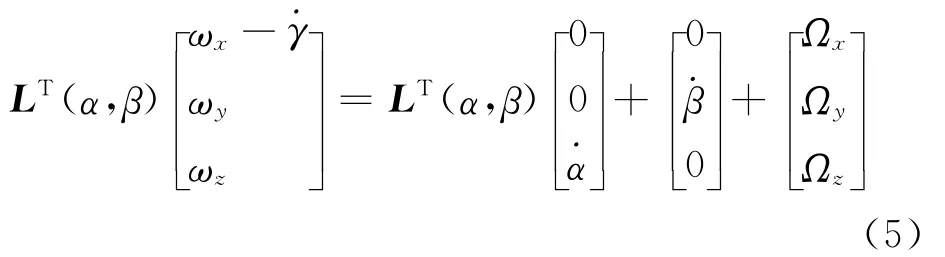
式（5）中，α、β为准速度与准弹体坐标系之间的攻角和侧滑角［1］；L（α、β）为相应的坐标系转换矩阵；ωx、ωy和ωz分别为弹体转动角速度在准弹体坐标系的投影为滚转角变化速率；Ω ＝ ［ΩxΩyΩz］T为准速度坐标系的转动角速度在准速度坐标系上的投影。

取观测系统的状态变量x＝［αβ］T，输入变量u＝ ［ωzωy］T，将式（6）展开并化简得到形如式（1）的攻角、侧滑角系统状态方程中各项

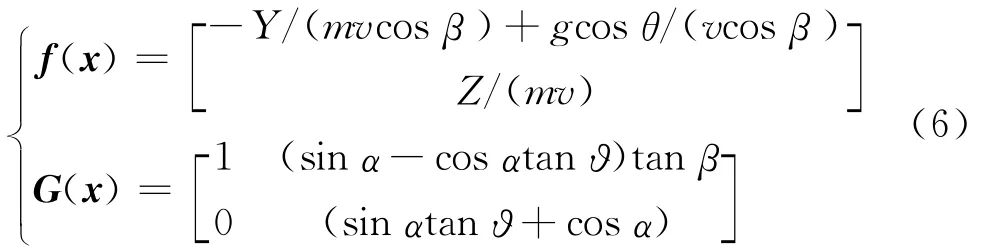
式（6）中，气动升力Y＝qSCy，侧向力Z＝qSCz，q为动压，S为弹箭特征面积，Cy、Cz分别为升力和侧向力系数，θ为弹道倾角，v为弹箭飞行速度。

由弹体所受力的投影关系可得到制导炮弹加速度的量测方程为：

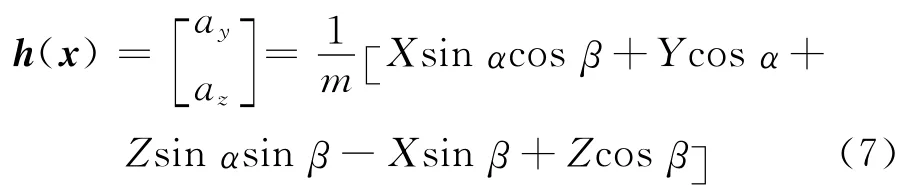
式（7）中，ay和az为视加速度在准弹体系下的投影，m为弹箭质量，气动阻力X＝qSCx，Cx为阻力系数。

在控制系统设计时，通常视舵偏为输入量，那么描述制导炮弹对象的攻角、侧滑角模型是耦合的四阶系统。这里假设可以通过加速度计、陀螺仪测得准弹体的加速度和角速度，并把角速度看成输入量，那么式（6）和式（7）便构成攻角、侧滑角的二阶观测系统模型，从而降低了观测器维数。

2.2 观测器结构与增益矩阵配置算法

由观测系统式（6）、式（7）可知相对阶ρ1＝ρ2＝1，与系统的阶数相同，不存在零动态。参考式（2）取Φ（x）＝ ［h1h2］T，将原非线性系统转化为式（4）的形式，然后参考线性系统的龙伯格观测器设计方法，可得到观测器动态方程［5］：

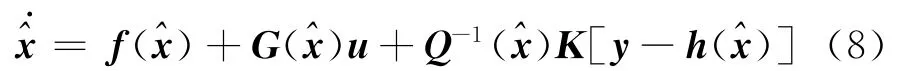
此观测器利用攻角与侧滑角动力学系统模型、弹体角速度和加速度测量预测误差等信息来重构制导炮弹的攻角、侧滑角。

观测器式（8）中的增益矩阵K反映了测量值对系统状态估计值的修正情况。设观测器误差~x＝x－＾x，则动态误差方程为

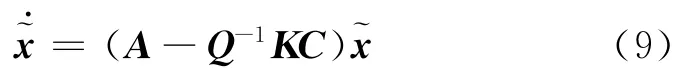
式（9）中，A＝∂f／∂x｜x＝＾x，C＝∂h／∂x｜x＝＾x。由式（9）可知，通过合理地调整增益矩阵K，可使动态误差系统稳定，从而实现对系统状态量精确重构的目的。考虑到本文建立了关于攻角、侧滑角的双输入双输出二阶观测系统的特点，若欲使动态误差按期望特性（~x＝eΛt~x0）快速收敛，对应的观测器增益矩阵K可按式（10）简单计算

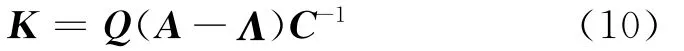
式（10）中，Λ ＝diag（λ1，λ2），λ1、λ2为期望的负实数。

3 非线性仿真与分析

设仿真初始条件：制导炮弹质量m＝40 kg，转速ωx＝11 r／s，初始速度v＝280 m／s，攻角α＝－5°、侧滑角β＝0.35°。同时假设含有较大的初始误差，观测器动态方程式（8）的初始值为＾α＝5.73°，＾β＝5.73°。为了考核观测器的性能，使等效舵偏δy按阶跃指令、δz按正弦指令偏转，图1、图2分别为该舵偏控制下产生的角速度变化和弹体视加速度测量曲线。

观察图1可知，在初始时刻与5 s时的阶跃偏航舵偏指令，将引起角速度的振荡，同时由于弹体的滚转使俯仰和偏航运动存在较强耦合，并引起图2所示的弹体受力情况。

观测器增益矩阵对攻角、侧滑角的重构效果有较大的影响。式（9）、式（10）可看出观测器指数矩阵Λ的对角元素绝对值越小，则观测器的时间常数越大，对真实值逼近的速度较慢，在对攻角重构时存在滞后，并且接受阶跃偏航舵控指令时，存在较大的动态误差。图3、图4为Λ＝diag（－15，－15）时的重构效果图，观测器估计值能快速逼近真实的攻角、侧滑角，改善了阶跃舵偏指令时的高频动态重构效果。值得注意的是，增大Λ虽可改善观测器的动态特性，但同时也降低了对噪声的抑制能力，因而在设计控制系统时应尽量避免控制律的阶跃突变。

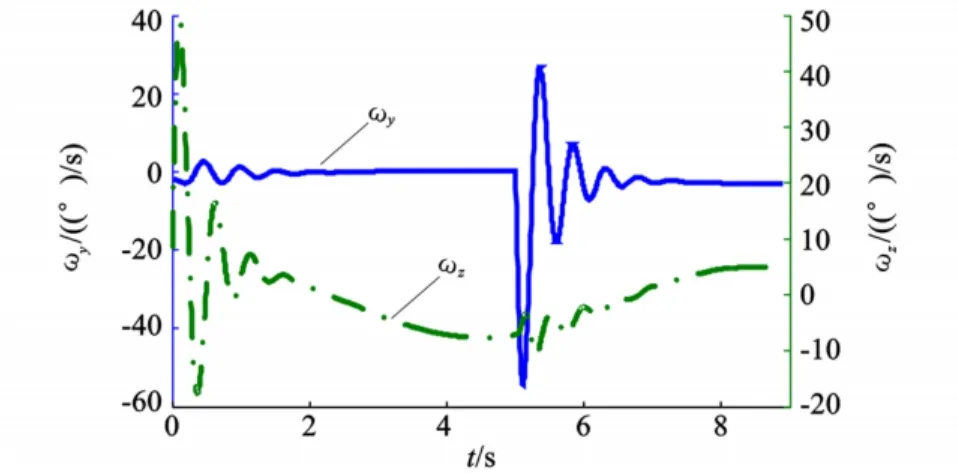
图1 弹体角速度曲线Fig.1 Curves of angle rate

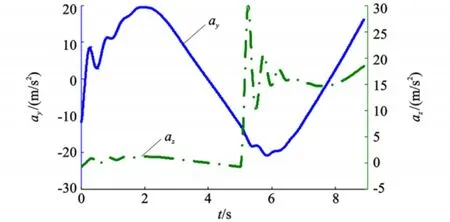
图2 弹体加速度曲线Fig.2 Curves of acceleration

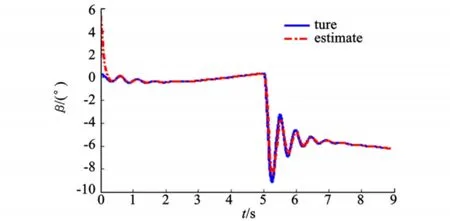
图3 侧滑角估计Fig.3 Side-slip angle esti mate

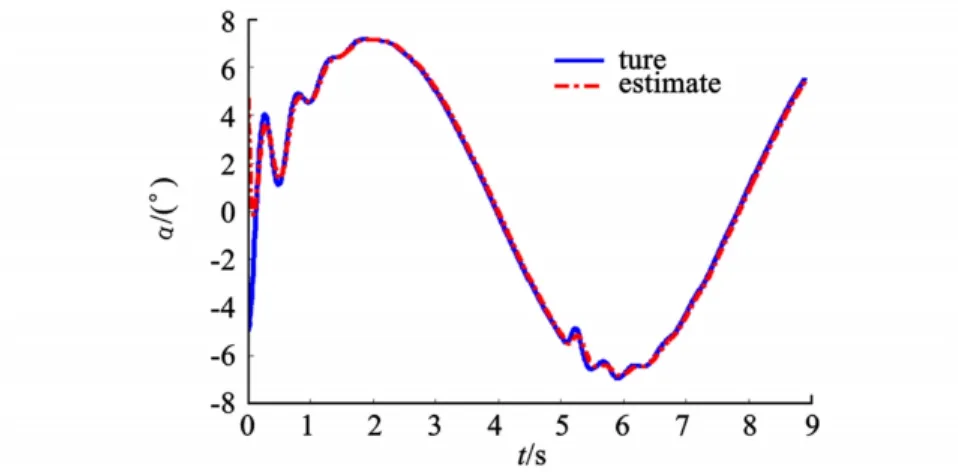
图4 攻角估计Fig.4 Angle of attack esti mate

4 结论

本文提出了一种基于坐标变换的制导炮弹攻角、侧滑角观测器。该观测器在采用了降阶的观测系统模型的基础上通过坐标变换的方法将系统解耦线性化，利用角速度、加速度信息实现对攻角侧滑角的估计，所对应的增益矩阵配置方法简便。数值仿真表明：该观测器能够有效地估计出制导炮弹的攻角与侧滑角，并且观测器结构简单，参数的物理意义明确，可合理调节使观测器具有期望的动态性能，易于工程实现。此外，考虑到通常制导炮弹的弹体频率较高，为较好地重构攻角、侧滑角，在控制系统设计时应尽量避免产生阶跃舵偏指令。

［1］韩晶，王华.基于反馈线性化的二维弹道修正控制系统设计［J］.弹道学报，2010，22（2）：27-31.HAN Jing，WANG Hua.Control system design f or 2-D trajectory corrector based on feedback linearization［J］.Jour nal of Ballistics，2010，22（2）：27-31.

［2］CLOUTIER J R，STANSBERY D T.Nonlinear，hybrid bank-to-tur n／skid-to-tur n missile autopilot design（AIAA-2001-4158）［C］／／2001 AIAA Guidance，Naviga-tion，and Control Conference and Exhibit.Montreal，Canada：AIAA，2001：1-12.

［3］MOON G Y，KI M Y D，CHO S B.Variable structure control with opti mized sliding surface for aircraft control system（AIAA2004-5420）［C］／／2004 AIAA Guidance，Navigation，and Control Conference and Exhibit.Rhode Island，USA：AIAA，2004：1-9.

［4］DAS A，DAS R.Nonlinear Autopilot and Observer Design for a Surface-To-Surface，Skid-To-Tur n Missile［C］／／Proceedings of the IEEE INDICON.Chennai，India：IEEE，2005：304-308.

［5］NAM H J，JIN H S.Input Output Linearization Approach to State Obser ver Design for Nonlinear System［J］.IEEE Transactions on automatic control，2000，45（12）：2 383-2 393.

［6］刘强，于达仁，王仲奇.高超声速飞行器的滑模观测器设计［J］.航空学报，2004，25（6）：588-592.LIU Qiang，YU Da-ren，WANG Zhong－qi.Sliding-mode observer design for a hypersonic vehicle［J］.Acta Aeronautica et Astronautica Sinica，2004，25（6）：588-592.

［7］LEE S，YEE Y，PARK M.An observer design for MI MO systems［J］.Transactions on control，automation and system engineering，2002，4（3）：189-194.

［8］SLOTINE J E，LI W.Applied nonlinear control［M］.Englewood Cliffs：Prentice Hall，1991.