基于幅度响应约束的稳健自适应宽带波束形成

陈明建，罗景青

（解放军电子工程学院电子对抗信息处理实验室，安徽 合肥 230037）

0 引言

自适应波束形成能增强期望信号并抑制干扰和噪声，已被广泛应用于雷达、声纳、语音处理和通信系统等领域［1－3］。当期望信号来波方向无误差时，传统自适应波束形成算法可以根据信号环境的变化，来自适应调整各阵元的加权因子，达到增强信号同时抑制干扰的目的［4－5］。但在期望信号来波方向存在偏差时，算法的性能会急剧下降，尤其在高信噪比时，有用信号会被当作干扰而受到抑制。如何提高自适应波束形成算法对波束指向偏差的稳健性一直是人们研究的热点问题。

目前存在多种有效的方法用来克服信号观察方向失配问题，最具有代表性的方法如：线性约束最小方差（LCMV）波束形成算法通过增加多个方向约束［6］和导数约束［7－8］，可减小算法对信号方向失配的敏感度，但同时要损失阵列的自由度。特征向量法采用信号子空间的信息估计权重向量，但是在低信噪比（SNR）条件下以及信号加干扰子空间的维数比较高时将会受到严重的制约和限制［9－10］。基于对角加载的波束形成算法是一种简单有效的方法［11－12］，但是加载量的确定一直是一个比较困难的问题。基于二次型不等式约束的稳健算法在本质上是属于可变对角加载的范畴，通过对权重向量所形成的空间指向性函数在阵列指向角附近小区域内的加权平方误差进行约束来提高阵列的稳健性［13－15］。

最近几年提出了基于模约束和不确定集约束的最差情况性能最优稳健算法［16－17］，该类算法的权矢量具有扩展对角加载的形式，根据导向矢量不确定集合可以确定最优加载量。基于波束响应幅度约束稳健算法在窄带情况下是一种简单有效方法［18］，对于宽带信号，该算法将增加许多的约束条件，不仅占用了系统的自由度，还增加了系统的复杂性。

针对以上问题，本文提出了一种基于幅度响应约束的稳健自适应宽带波束形成算法。

1 阵列模型与LCMV波束形成器

1.1 阵列模型

考虑D个宽带远场平面波入射到M元各向同性的均匀线阵上，阵元间距d为信号最高频率对于半波长，其中期望信号的波达方向为θ0，其余D－1个宽带以阵列的第0号阵元为参考阵元，每个阵元后有一个J阶FIR滤波器，每个节拍后的时延为Ts，Ts为时间采样周期。阵列结构如图1所示。

第m号阵元接收到的信号为：

式（1）中，s0（t），s1（t），…，sD－1（t）为期望信号与干扰信号在参考阵元上的实包络信号波形；τm（θ0），τm（θ1），…，τm（θD－1）为对应信源传播到第m号阵元相对于参考阵元的传播时延；nm（t）为第m号阵元上零均值高斯白噪声。若第m号阵元的样本数据记为xm（n）＝xm（t）t＝nTs，则该阵元其他各节拍数据为xm（n－ （k－1）） ＝ xm（t－ （k－1）Ts）t＝nTs，k ＝1，2，…J。假设wm，k是对应于第m号阵元第k个节拍的实权值，则波束输出信号时间序列可表示为：

1.2 LCMV波束形成器

线性约束最小方差（LCMV）算法是通过约束期望方向或干扰方向的响应并最小化阵列输出功率，以获得良好的干扰抑制性能，其等价为如下约束优化问题：

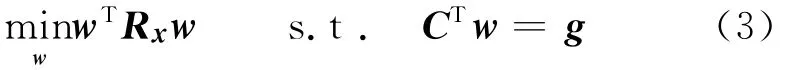
式（3）中，Rx为协方差矩阵，C为约束矩阵，可约束单个或多个方向，即由期望或干扰方向的导向矢量组成，g为相应的约束值矢量。其最优解为：

当期望信号的波达方向精确已知时，信号导向矢量无偏差，LCMV波束形成器能够提供无畸变的期望信号输出，同时能够最大程度地抑制干扰和噪声。但在期望信号波达方向估计不准确时，导向矢量将出现偏差，波束输出的性能会急剧下降。尤其在高信噪比时，有用信号会被当作干扰而受到抑制，造成信号相消问题，导致输出SINR值下降。

2 幅度响应约束和SRV约束的稳健宽带波束形成方法

该算法首先通过对阵列波束指向附近范围内的宽频段阵列响应与参考频率对应方位的阵列响应误差模值进行约束，使阵列波束图在主瓣区域内的信号畸变最小，其波束图近似保持频率不变特性，然后利用窄带波束响应幅度约束的稳健算法，在参考频率上对阵列波束指向附近范围内的波束响应幅度施加约束，同时增加对权矢量的范数约束，来克服信号方向失配的影响，提高自适应算法的稳健性，并以损失较少阵列自由度来改善波束输出性能。

2.1 幅度响应约束的稳健方法

首先考虑窄带情况，考虑阵列与目标源位于同一平面的情况，基阵对信号方向为θ的波束响应为P（）θ＝wTa（）θ，波束的幅度响应约束可以表示为：

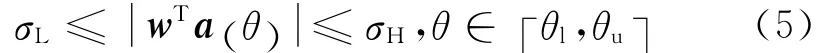
式（5）中，［σL，σH］为稳健方位区域 ［θl，θu］上波束的幅度响应抖动范围，a（θ）为窄带阵列的导向矢量。幅度响应约束的权矢量优化的准则是在满足一定方位区域的幅度响应约束条件下，同时使阵列输出功率最小，即w为下面优化问题的解：

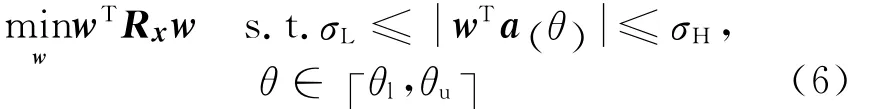
式（6）可以通过凸优化法求解权矢量。图2为窄带基于幅度响应约束的稳健波束形成的波束图。

图2 窄带幅度响应约束的波束图Fig.2 Narrowband beam-pattern withamplitude response constraints

基于上述讨论，可将窄带幅度响应约束思想推广到宽带情况，假定宽带信源的频段范围为Ω＝］，则波束响应幅度约束宽带稳健方法可表示为式（7）的约束优化问题：

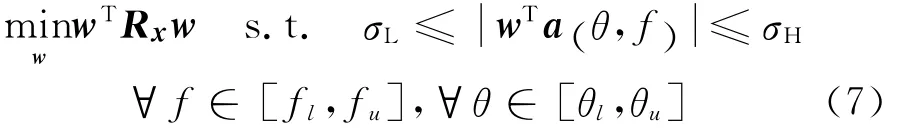
假设把宽带信源频段分为K个子带，并用fk表示为第k个子带的中心频率，即用K离散化的频率fk∈Ω，k＝1，2，…K来近似表示频率集合Ω。若直接运用窄带稳健算法，分别使K个子带的波束响应幅度约束，即满足式（7）的约束条件可实现宽带稳健算法。但上述基于子带划分的优化问题有2 K个约束条件，当信号带宽较宽，即子带划分个数K较大时，过多的约束将损失阵列的自由度，降低阵列输出SINR性能，且还会增加算法的复杂性和计算量。

2.2 本文方法

为了解决上述问题，本文提出了通过约束空间响应偏差，并利用频率不变技术结合窄带波束响应幅度约束的稳健算法，解决传统子带划分的宽带稳健算法中，过多约束条件而损失阵列自由度，导致波束输出的SINR性能下降的问题，同时减少了信号失真和优化算法的计算量和复杂度。

定义阵列空间响应偏差（Spatial Response Variation）SRV为在主瓣区域内（可设置为期望信号的波达方向偏差范围），频率范围Ω上的阵列响应与在某参考频率fr的阵列响应的误差模平方，即：

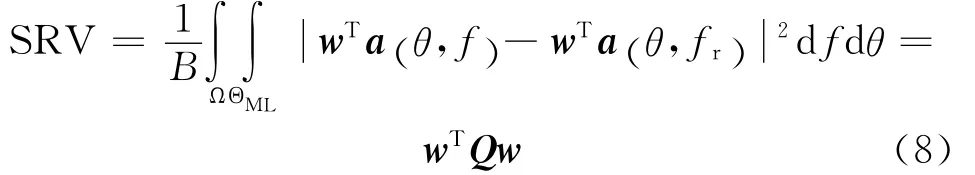
式中，B＝fu－fl，表示宽带信源的带宽，ΘML＝［θl，θu］为期望信号的波达方向偏差范围，Q为Hermite对称矩阵，

Re（）·表示取实部操作。

通过对式（8）分析可知，当SRV为零时，该波束器即满足频率不变特性，信号能够无失真输出，因此为了解决传统基于子带划分宽带稳健算法中，过多约束条件而导致波束输出SINR性能下降的问题，并尽可能的减少信号失真，可以通过控制主瓣区域的SRV值，使阵列波束图在宽频段内有近似恒定的主瓣响应，然后对参考频率fr处的波束幅度响应施加约束，并对权向量的范数进行约束，式（7）可以改写为如下约束优化问题：

式中，ε为非负实数，表示空间响应偏差的上限，δ为正实数，为加权矢量范数的上限。

由于式（10）中第三个约束条件的左边不等式为半无穷非凸问题，难以求解，因此可以将非凸问题近似转化为凸优化问题，即：

对矩阵Rx进行Cholesky分解，即Rx＝UT0U0，则得到

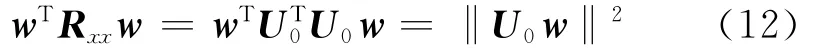
同理 可 得wTQw ＝ ‖U1w‖2。注 意 到 使‖U0w‖2最小化等价于使‖U0w‖最小化，引入一个非负标量β，并对方位区域离散化，式（10）可转化为如下凸优化问题：

3 计算机仿真

为了验证本文方法的有效性，分别采用以阵列输出信干噪比SINR、归一化信号失真NSD，以及归一化均方误差NMSE来衡量波束形成器的性能。

以下仿真实验若无特殊说明，均在各向同性的8元均匀线阵模型下完成，阵元间距为信号最高频率对应的半波长。空间存在一个期望目标信号和两个不相关的干扰信号，假设期望目标信号的入射方向为0°，而实际波达方向为3°，即存在3°的波束指向误差；干扰信号方位角分别为－40°和30°，功率均为30 d B。假定宽带信号的归一化工作频带考频率fr＝0.45，每个阵元后节拍阶数J＝18。此外，各通道噪声为不相关高斯白噪声，功率0 d B。其他参数设置如下：权矢量范数的上限δ＝0.6，主瓣区域的空间响应偏差上限分别为ε＝10－5，幅度响应约束的上限、下限值分别为σH＝10rdB／20、σL＝10－rdB／20，rdB为幅度响应抖动值，单位为d B。所有统计实验结果均由100次Monte-Carlo实验平均得到。

为方便讨论，将文献［18］中最坏情况下性能优化稳健自适应波束形成方法记为RB-WC算法，而本文所提基于幅度响应约束的稳健波束形成方法记为RB-CMR算法。

3.1 实验1

考察3种算法阵列方向图情况。

设输入信噪比SNR＝0 d B，干噪比JNR＝30 d B，rdB＝0.3 d B。图3（a）、图3（b）和图3（c）分别给出了信号方向存在偏差时3种算法的阵列方向图。

图3 三种算法阵列方向图Fig.3 Array patter ns of t hree algorith m

从图3中可以看出，LCMV算法在真实期望信号波达方向处波束指向出现偏差，且最大零陷位置偏离了干扰目标方向，其性能最差；RB-WC算法对系统的稳健性能有所改善，但无法控制稳健的方位区域宽度，而且干扰零陷位置也有所偏移；而本文所提的算法在信号方向存在偏差的情况下，波束增益最大方向与信号真实方向的偏差较小，且有一定的稳健的方位区域宽度，零陷位置准确对准干扰方向，有助于提高阵列的SINR性能。

3.2 实验2

考察本文算法在不同稳健参数情况下的波束图。

仿真条件不变，本文算法在不同稳健参数情况下的波束图如图4所示，该法可灵活控制稳健的方位区域宽度和相对应方位范围的波束幅度响应的抖动值。

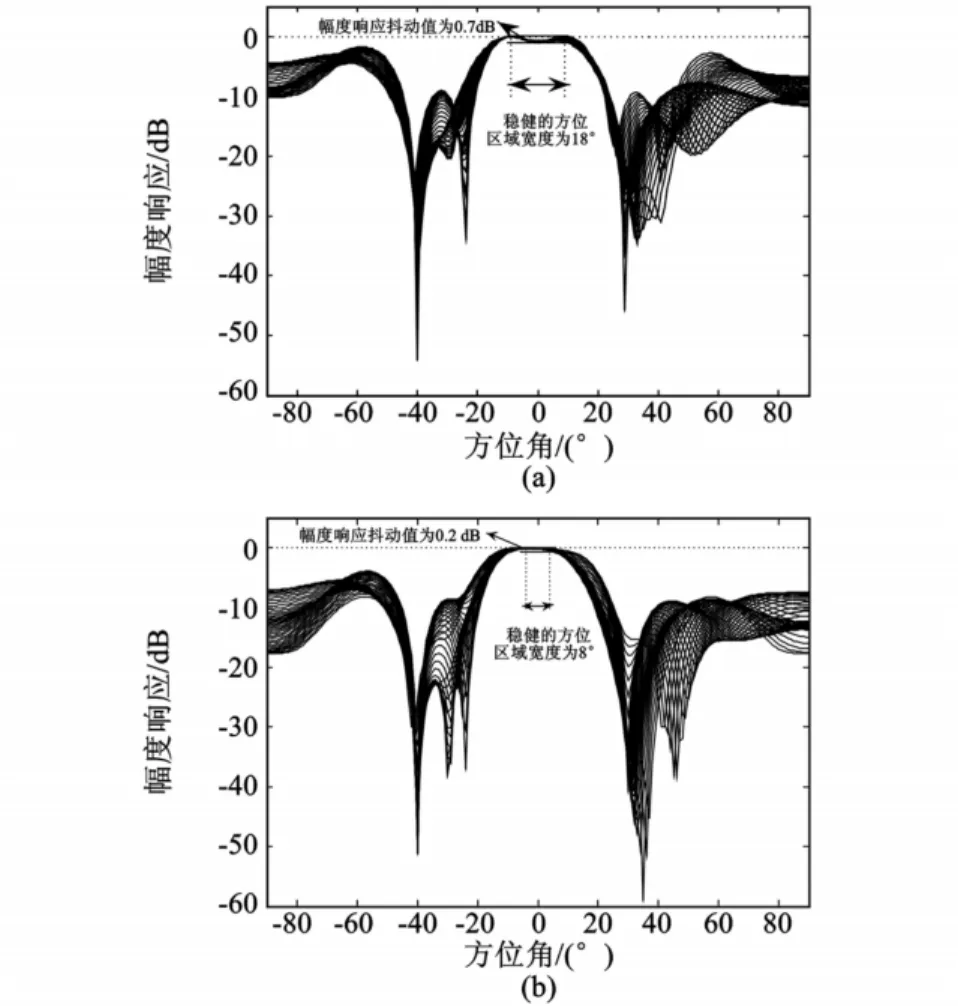
图4 不同稳健参数时的波束图Fig.4 Beam-patter n with different robust parameters

3.3 实验3

考察不同采样快拍数与输入SNR情况下的波束输出SINR性能。

3种算法波束输出SINR与采样快拍数N的关系如图5所示，其中SNR＝0 d B。图中3条曲线均随着快怕数N的增加迅速收敛并趋于平稳，其中常规的LCMV算法由于不具有稳健性能，收敛后的SINR值最小，而两种稳健算法的SINR性能较前者有较大改善，且本文算法优势更明显。这是由于通过增加空间响应偏差约束，减少约束优化模型的约束不等式个数，因此本文方法将有更多的阵列自由度用于改善SINR性能。

图5 输出SINR与采样快拍数的关系Fig.5 The relationship bet ween output SINR and the number of sample snapshots

图6 为3种算法波束输出SINR与输入SNR的关系曲线。由图6可知，本文算法波束输出的SINR性能要优于常规LCMV算法和RB-WC算法，尤其在高SNR时，这种优势更加明显。这是因为本文算法在提高阵列稳健性的同时，减少了优化模型的约束条件个数，从而有更多阵列自由度用于改善波束输出的SINR性能。

图6 输出SINR与输入SNR的关系Fig.6 The relationship bet ween output SINR and input SNR

3.4 实验4

考察在不同输入SNR情况下，波束输出期望信号失真NSD与归一化均方误差NMSE性能。

图7是阵列波束输出的归一化信号失真NSD随信噪比SNR的变化曲线。由图7可知，在信号方向存在偏差时，常规的LCMV波束输出信号有较大信号失真，随着输入SNR的增加，波束输出信号失真更严重，而两种稳健算法的NSD值对输入SNR不敏感，具有较强的稳健性，但由于本文算法增加了频率不变约束，其NSD值更小，降低波束形成对信号失真的影响。

图7 归一化信号失真NSD与输入SNR的关系Fig.7 The relationship bet ween NSD and input SNR

图8 为波束输出归一化均方误差NMSE随信噪比SNR变化曲线。由图8可知，与常规LCMV算法和RB-WC算法相比，本文算法的NMSE性能均优于上述两种算法，在输入SNR＞15 d B时，其NMSE几乎为零，由此可见，本文算法对信号方向误差有更强的稳健性，波束输出的总体性能最佳。

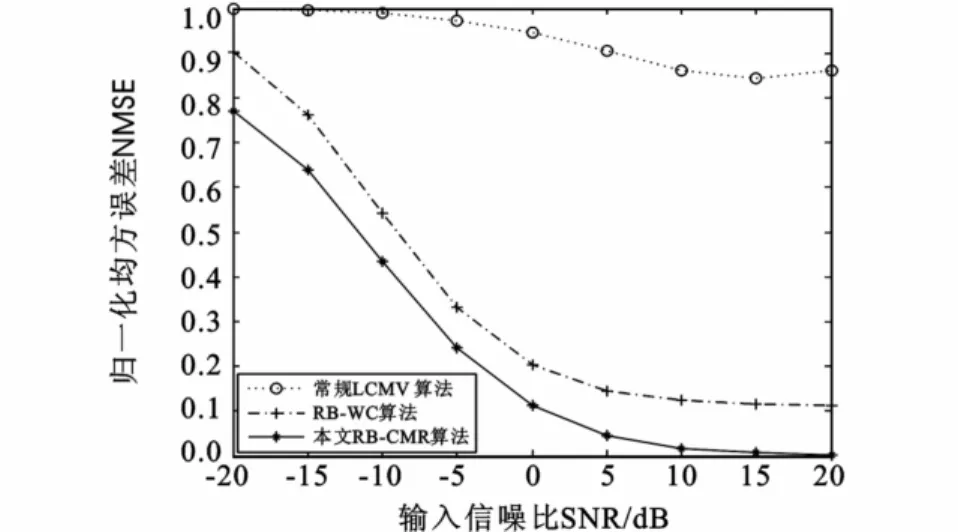
图8 归一化均方误差NMSE与输入SNR的关系Fig.8 The relationship bet ween NMSE and input SNR

4 结论

本文考虑期望信号方向存在偏差时，常规自适应波束形成算法的性能将会急剧下降的问题，提出了一种基于幅度响应约束的稳健自适应宽带波束形成方法。该方法通过对阵列波束指向附近范围内的波束幅度响应施加约束来提高阵列的稳健性，并增加阵列空间响应偏差约束与权重向量的范数约束，减少了约束优化不等式的个数，进一步提高该方法的波束输出SINR性能和稳健性，降低算法的计算量。计算机仿真结果表明：与稳健的RB-WC方法相比，本文方法对信号方向存在偏差有更强的稳健性，且能有效控制波束稳健区域宽度和幅度响应的抖动值，更加有效地抑制干扰信号，使阵列波束输出性能均优于稳健的RB-WC方法。

［1］Van Trees H L.Opti mu m Array Pr ocessing，part IV of Detection，Esti mation，and Modulation Theor y［M］.New Yor k：John ＆ Sons，Inc.Wiley，2002.

［2］Liu W，Weiss S.Wideband Beamfor ming：Concepts and Techniques［M］.U.K：Chichester，Wiley，2010.

［3］Do-hong T，Russer P.Signal processing f or wideband s mart antenna array application［J］.IEEE Microw Mag，2004（1）：57-67.

［4］Lin N，Liu W，R J Langley.Perfor mance analysis of an adaptive broadband beamfor mer based on a t wo-element linear array with sensor delay-line pr ocessing［J］.Signal Processing，2010，90：269-281.

［5］Yu L，Lin N，Liu W，et al.Band width perf or mance of linearly constrained mini mu m variance beamfor mer［J］.IEEE international workshop on antenna technology，2007：327-330.

［6］Frost III O L.An algorith m for linearly constrained adaptive array processing［J］.Proceeding of IEEE，1972，60（8）：926-935.

［7］Buckley K M，Yeh C C.Perfor mance analysis of derivate constraint adaptive arrays with pointing errors［J］.，IEEE Trans.Antenna Propag，1992，40：975-981.

［8］Zhang S，Thng I L J.Rubost prestreering derivative constraints for broadband antenna arrays［J］.IEEE Trans Signal Processing 2002，50：1-10.

［9］Feld man D D，Griffiths L J.A projection approach to robust adaptive beamfor ming ［J］.IEEE Trans on Signal Pr ocessing，1994，42（4）：867-876.

［10］赵永波，张守宏.基于特征空间的线性约束最小方差波束形成器［J］.电子与信息学报，2005，27（3）：423-426.ZHAO Yongbo，ZHANG Shouhong.Eigenspace-Based Liearly Constrained Minimu m Variance Beamfor mer［J］.Jour nal of Electronics ＆Inf or mation Technology，2005，27（3）：423-426.

［11］Carlson B D.Covariance matrix esti mation errors and diagonal loading in adaptive arrays［J］.IEEE Trans.on Aerosp Electron Syst，1988，24（7）：397-401.

［12］Van Veen B D.Mini mu m variance beamfor ming with soft response constraints［J］.IEEE Trans Signal on Processing，1991，39（9）：1 964-1 972.

［13］Duan H P，Boon P N，M S S Chong，et al.Applications of the SRV constraint in broadband patter n synthesis［J］.Signal Processing，2008，88：1 035-1 045.

［14］宋昕，汪晋宽，韩英华.基于二次型约束的鲁棒自适应波束形成算法［J］.电子与信息学报，2008，30（11）：2 662-2 665.SONG Xin，WANG Jinkuan，HAN Yinghua.Robust A-daptive Beamfor ming Algorith m with a Quadratic Constraint［J］.Jour nal of Electronics ＆Inf or mation Technol-ogy，2008，30（11）：2 662-2 665.

［15］Boon Poh Ng and Huiping Duan.Designing amplitude／phase respose of the frost bea mf oner［J］.IEEE Trans.on Signal Processing.2007，55（5）：1944-1949.

［16］Vorobyov S A，Gersh man AB，Luo Z-Q.Robust adaptive beamfor ming using worst-case perf or mance opti mization：A solution to the signal mis match problem［J］.IEEE Trans Acoust，Speech，Signal Processing，2003，51：313-324.

［17］Rubsamen M，Gersh man A B.Robust presteered br oadband beamf or ming based on worst-case perf or mance optimization［C］／／IEEE Workshop on Sensor Array and Multichannel Signal Processing.Dar mstadt：IEEE，2008：340-344.

［18］Yu Z L，Ser W，Er M H，Gu Z H，Li Y Q.Robust adaptive beamfor mers based on worst-case optimization and constraints on magnitude response［J］.IEEE Transactions on Signal Pr ocessing，2009，57：2 615-2 628.

［19］Stur m J K.Using Se Du Mi 1.02，a Matlab toolbox for opti mization over sy mmetric，Opti miz［J］.Meth，Software，1999，（11-12）：625-653.