基于公式近似的末敏弹扫描角计算方法

马凯臣，曹咏弘，范锦彪

（中北大学电子测试技术国家重点实验室，山西 太原 030051）

0 引言

末敏弹是一种灵巧弹药。末敏弹通过旋转减速伞或者弹翼使其保持稳定的落速和转速，进入稳态扫描阶段，同时用传感器对目标进行搜索，一旦发现目标就进行打击。因此，在末敏弹的研制过程中，需要测量末敏弹在稳态扫描阶段的下落速度、扫描角和扫描角速度等参数［1］。

目前国内测量末敏弹扫描角的主要方法有：基于地磁传感器的方法和基于角速度陀螺和加速度计组合的方法。根据文献［1］，基于地磁传感器的测量方法，优点在于解算扫描角时为直接计算，不存在累积误差；但是这种方法，由于其受周围磁场变化（如弹体自身剩余磁场）影响较大，在测量末敏弹的扫描角时误差较大［2］。传统的基于角速度陀螺和加速度计组合的测量方法，优点在于相关理论成熟，能够测出每一时刻的扫描角大小；但是在解算时需要初始姿态角，容易有初始误差，而且在解算过程中存在累积积分误差，此误差随时间增加不断增大［3］。

由于末敏弹在稳态扫描阶段扫描角速度能达到4～6 r／s，因此采用的角速度陀螺的量程也比较大，例如实验室采用的就是±2 000（°）／s的角速度陀螺；然而大量程的角速度陀螺，在测量精度上往往比较低，这样就更加大了累积积分误差。这一点在末敏弹扫描角的解算上体现得尤为明显。

利用角速度陀螺来测量末敏弹稳态扫描阶段的扫描角和扫描角速度，存在着一些问题。由于末敏弹在稳态扫描阶段扫描角速度能达到4～6 r／s，因此采用的角速度陀螺的量程也比较大，例如实验室采用的就是±2 000（°）／s的角速度陀螺；然而大量程的角速度陀螺，在测量精度上往往比较低。一般的解算方法是，在已知初始姿态角的情况下，将弹体上角速度陀螺测得的数据进行坐标变换，进行积分，从而得到姿态角。这样积分得到结果，误差会很大，这一点在末敏弹扫描角的解算上体现得尤为明显。为了克服这些缺点，本文提出了计算末敏弹稳态扫描阶段扫描角的方法。

1 积分计算原理

描述末敏弹运动的运动学方程，表述如下。定义惯性坐标系为Oxyz，弹体坐标系为Oxbybzb。通常，在描述末敏弹的运动特性时，是用3个欧拉角α，β，γ来描述［4］的：

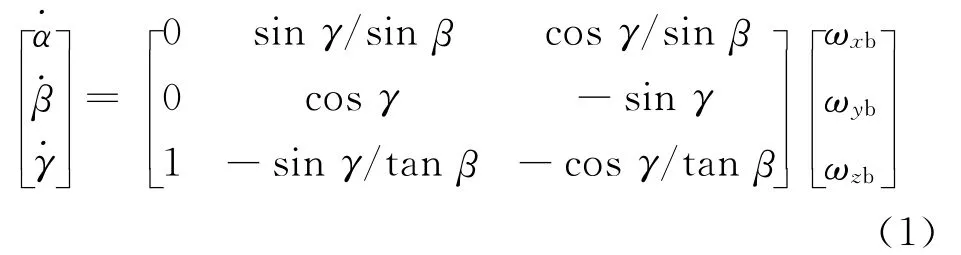
式（1）中，α为进动角；β为章动角，即弹轴与铅直轴的夹角；γ为自转角；ωxb，ωyb，ωzb分别为弹体在x，y，z方向上的角速度，由三维角速度陀螺直接测得。在末敏弹稳态扫描阶段中，扫描角速度就是进动角α的微分，扫描角就是章动角β。

积分解算方法就是在已知初始姿态角的情况下，根据式（1）进行积分，从而解算出来扫描角（即章动角）β。但是这种方法解算的误差比较大，而且误差会积累。

2 基于公式近似的计算方法

对于上述公式进行适当的变化和近似，就可以得到直接测量扫描角的方法。由式（1）可得：

从而可以得到：

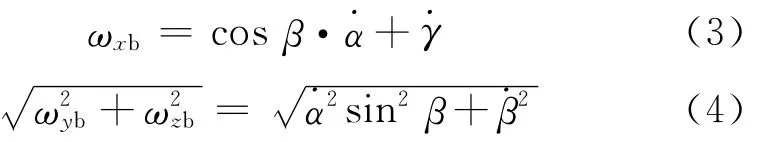
一般在末敏弹的稳态扫描过程中，进动角速度˙α通常在4～6 r／s。在末敏弹的稳态扫描阶段，扫描角的大小是比较稳定的，因此章动角即扫描角的变化率˙β很小，与进动角速度˙α相比，可以忽略。同时，在稳态扫描过程中，通过对实际数据观测，发现自转角的角速度˙γ几乎接近于0，也可忽略。因此可得：

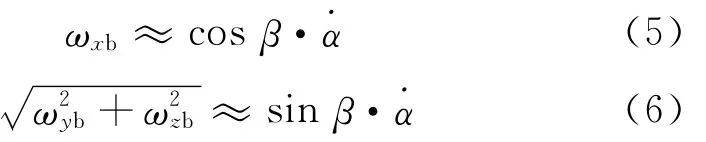
通过上面两式，可以得到扫描角β为：

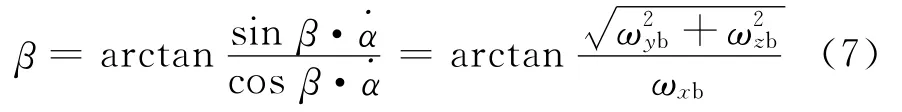
根据上述近似可以知道，当进动角速度˙α比较小的时候，测量的误差会很大；当进动角速度˙α较大的时候，就能够准确地测量扫描角β。

根据公式（1），影响积分法误差计算精度的有初始姿态角和角速度的误差。由于角速度误差的存在，随着时间的推移，姿态角α，β，γ的误差会越来越大［5］。设α，β，γ的初始值为α＝0°，β＝30°，γ＝0°，弹体角速度ωxb，ωyb，ωzb的值为末敏弹做扫描角速度为200（°）／s的扫描运动时的理想值，进行仿真，解得扫描角曲线如图1所示。

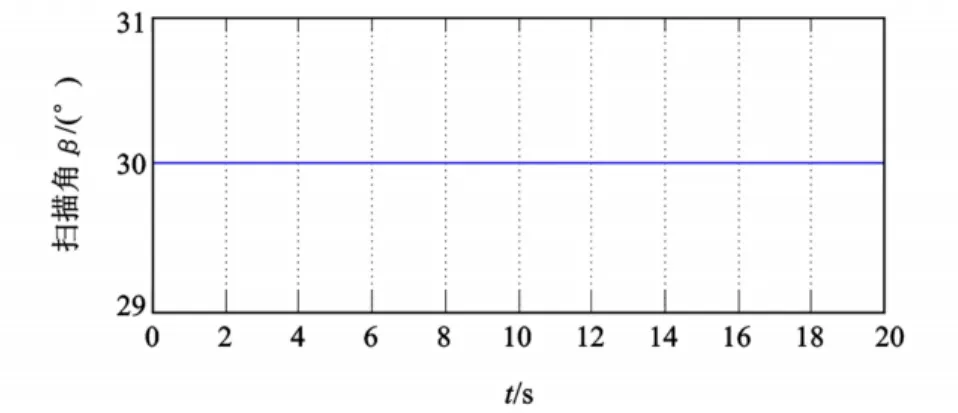
图1 理想情况仿真曲线Fig.1 Si mulation curve under ideal state

现在考虑初始值中存在误差的情况。将仿真值中的β的初始值改为β＝31°，即扫描角β存在1°的误差，其余仿真值不变，进行仿真，解得扫描角曲线如图2所示。

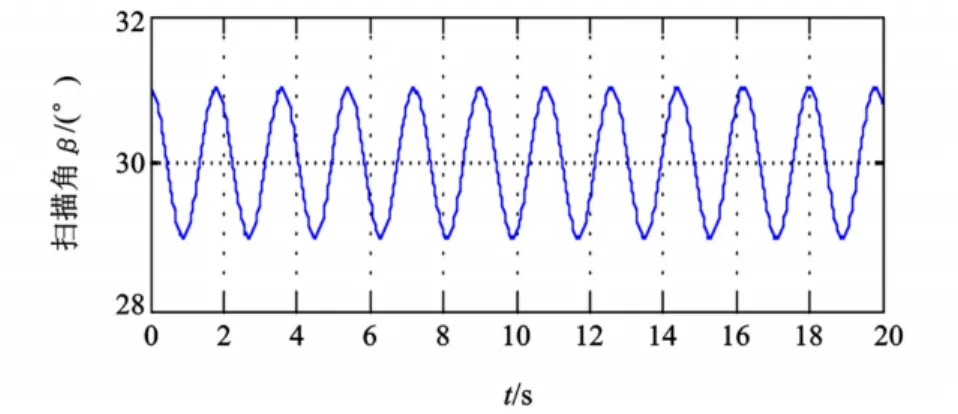
图2 初始值存在误差情况仿真曲线Fig.2 Simulation curve with initial error

可见，在其余值均为理想值的情况下，初始姿态角的误差在积分法中不会消失。也就是说，在积分法解算的过程中，一旦出现了误差，这个误差将一直存在，并将积累。

而对比上述分析，再根据公式（7），影响直接计算法精度的只有角速度ωxb，ωyb，ωzb的误差，并且直接计算法的误差不会积累，这说明了直接计算法的优势。

3 实验验证

3.1 转台模拟实验

为了比较传统积分方法和公式近似法在解算扫描角时的误差大小，我们设计并进行了转台模拟实验。实验所用的转台为高精度的三轴转台，其转速范围为±300（°）／s，误差小于1‰。我们设计的实验是模拟末敏弹以30°的扫描角进行稳态扫描运动的情况。将惯性测量单元固定到转台上，然后将转台绕y轴逆时针旋转30°，这样惯性测量单元的x轴就与竖直轴有了一个30°的夹角。然后启动转台，令转台以200（°）／s的转速绕竖直轴进行旋转。这样就模拟了末敏弹以30°的扫描角进行稳态扫描运动的情况。

固定在转台上的三维角速度陀螺采集到的数据如图3所示。

从图中可以看出，从惯性测量单元开始记录起，在大约不到8 s的时候转台开始加速，在大约14 s的时候达到了设定的转速值，之后开始匀速旋转。

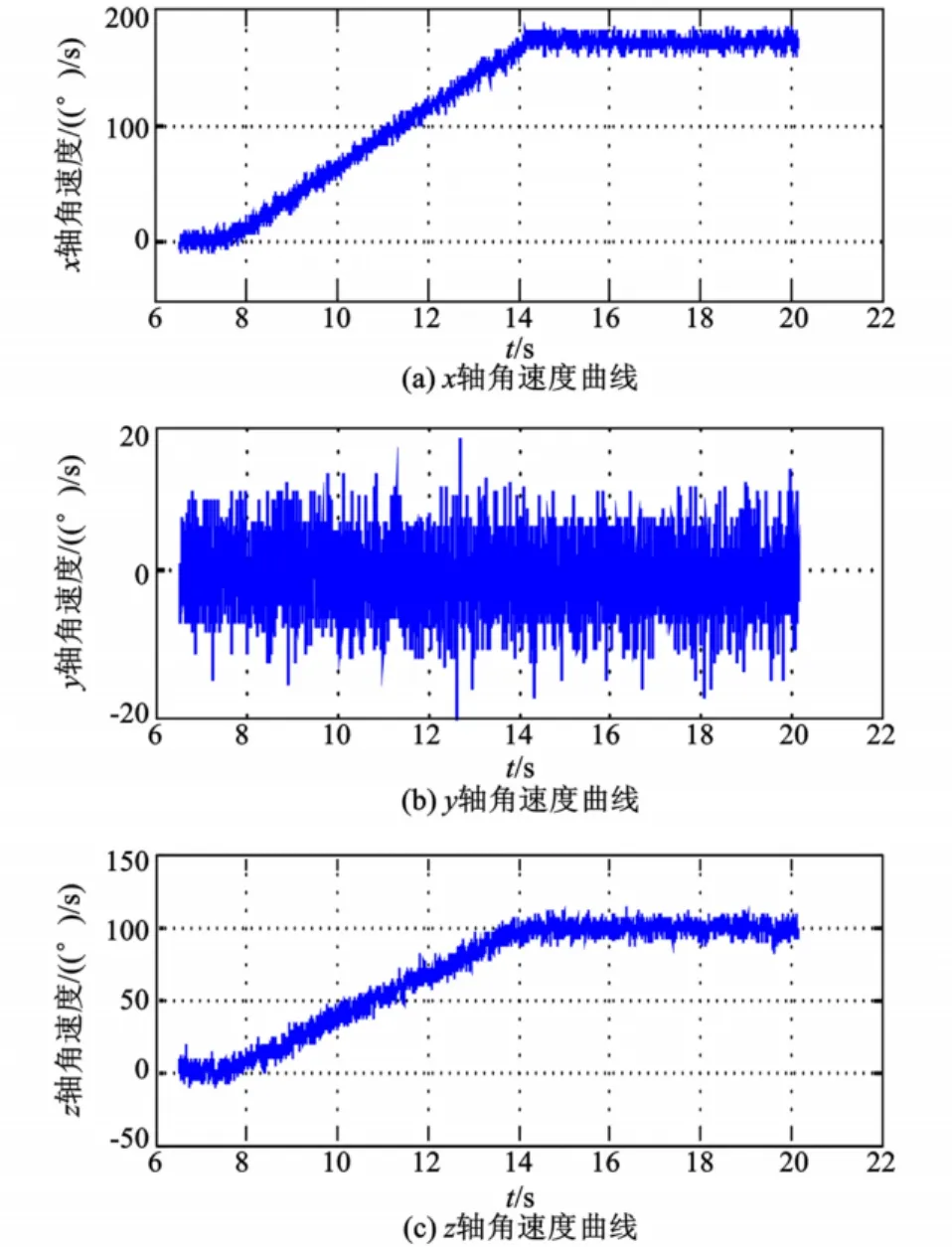
图3 转台实验三维陀螺数据Fig.3 Three-axis gyro data of tur ntable experi ment

用积分方法解算得到的结果如图4所示。

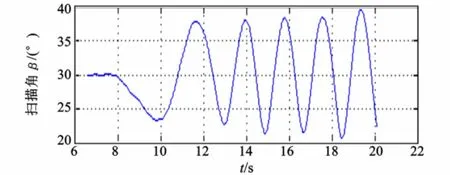
图4 转台实验积分法解算结果Fig.4 Result of integration method of turntable experi ment

利用上一节公式（7）所述方法，解算得到的扫描角曲线如图5所示。

从图5（a）中可以看出，大约在11 s之前，解算来的扫描角并不正确，这之前转台处于未启动或者转速较低的阶段。在这之后，能够解算出正确的角速度。符合上一节的推测。从图5（b）中可以看出，虽然由于陀螺的输出本身存在随机误差，解算结果有一定的随机变化，但是解算出来的误差在1°之内，要优于积分方法。

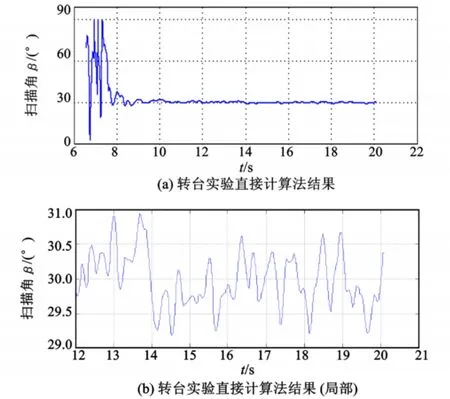
图5 转台实验直接计算法结果Fig.5 Result of directly calculating of turntable experi ment

3.2 仿真投弹实验

下面给出在实际末敏弹参数测量实验中，公式近似法解算的结果，并与传统积分解算方法的结果进行比较。在末敏弹的研制过程中，需要进行仿真投弹实验。高塔投弹实验就是一种仿真投弹实验。高塔投弹实验的过程是将实验用的末敏弹人工从高塔上投掷下去，末敏弹会出现一些大幅的摆动，然后再进入稳态扫描阶段，直到最后落地。在这一过程中弹体内的惯性测量单元会记录数据。本次进行的高塔投弹实验，塔高125 m，天气状况晴朗无风。图6是某型伞降末敏弹在高塔投弹实验中三维角速度陀螺测得的数据。

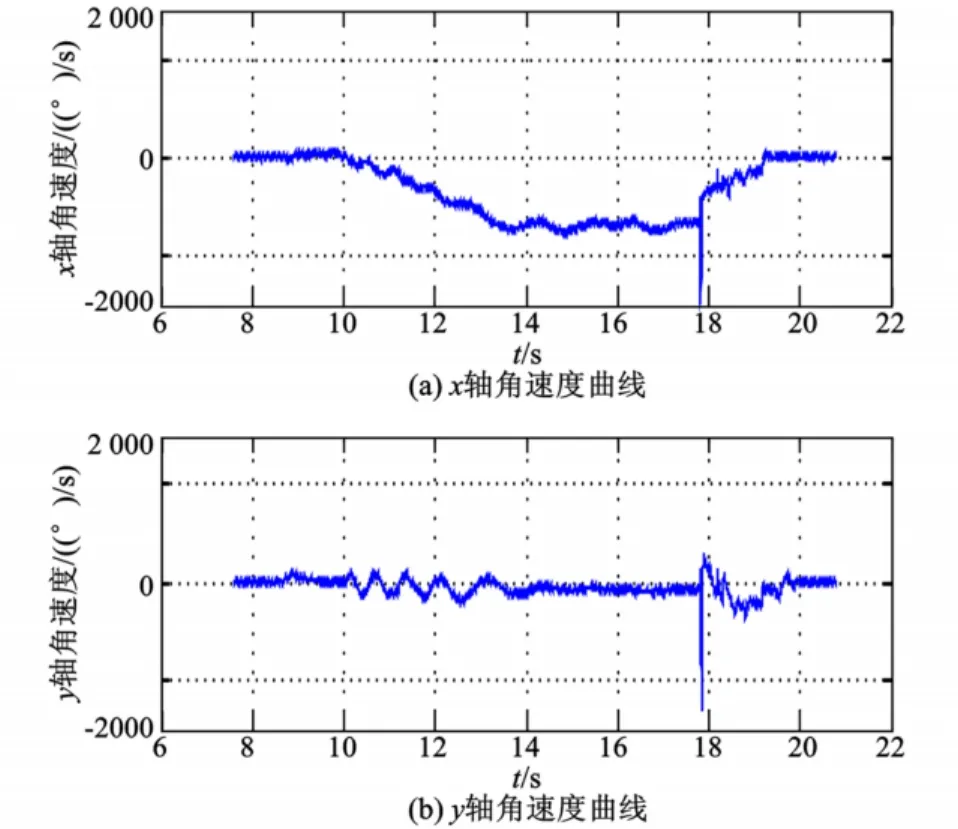
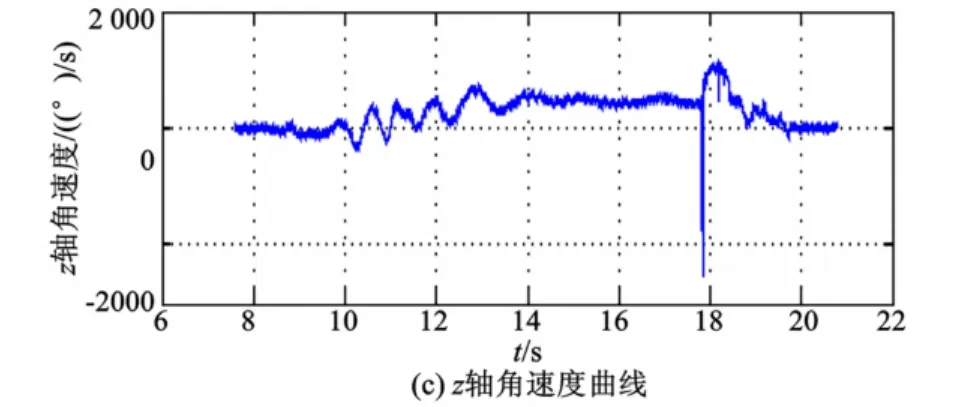
图6 仿真投弹实验三维陀螺数据Fig.6 Three-axis gyro data of si mulation bo mb-dropping test

从记录仪开始计时起，在10 s左右弹体开始产生旋转；在14 s左右，x轴的转速达到最大，并且保持相对稳定，进入了稳态扫描阶段；在18 s左右，弹体撞地。

图7是积分法解算得到的扫描角。在14 s以后，扫描角大体在20°左右，但是解算结果摆动的比较大。

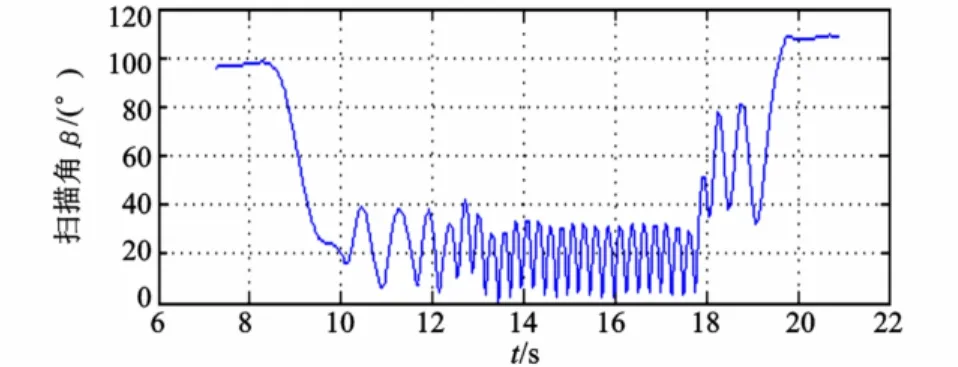
图7 仿真投弹实验积分法解算结果Fig.7 Result of integration method of simulation bo mb-dropping test

图8 是直接计算法解算得到的扫描角。由图8可知，在14 s后，即在稳态扫描阶段，解算出的扫描角稳定在18°左右，直到最后弹体撞地。图7、图8进行比较，可见解算精度优于积分法得到的结果。

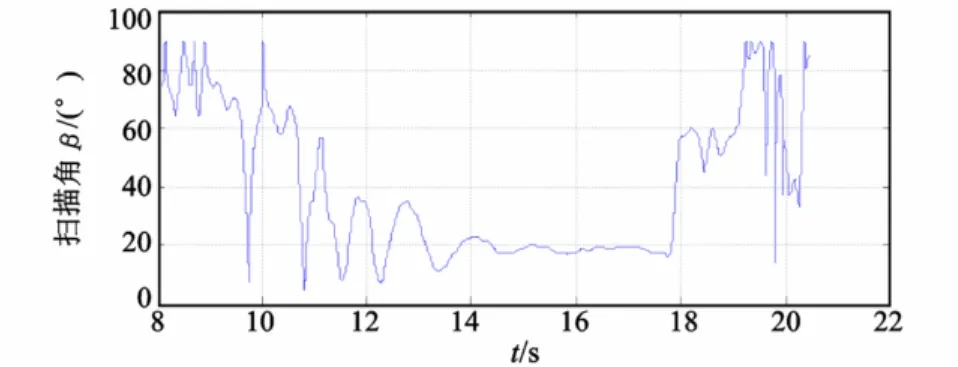
图8 仿真投弹实验直接计算法结果Fig.8 Result of directly calculating of si mulation bo mb-dropping test

4 结论

本文提出了一种利用三维角速度陀螺的数据来直接计算末敏弹的扫描角的方法，并且用实验证明了它的可行性和优越性。这个方法的创新点在于，根据末敏弹在稳态扫描阶段进动角速度很大而章动角变化很小的特点，利用弹体上的三维角速度陀螺来直接计算扫描角，提高了解算精度。直接计算法比积分计算法的精度要高，一是因为计算方法简单，引入的误差源少；二是因为积分计算法存在着累积误差。该方法可以广泛用于末敏弹扫描角的测量。

［1］李良华.无伞末敏弹稳态扫描运动参数的测量技术研究［D］.南京：南京理工大学，2009.

［2］刘晓娜，马铁华.地磁传感器及其在姿态角测试中的应用研究［D］.太原：中北大学，2008.

［3］David H Titterton，John L Weston.Strapdown Inertial Navigation Technology［M］.USA：AIAA，2004.

［4］刘怡昕，刘玉文.外弹道学［M］.北京：海潮出版社，1998.

［5］Mark Looney.A simple calibration f or MEMS Gyroscopes［J］.EDN EUROPE，2010（1）：198－201.