一题三解,各具特色

430223 武汉市光谷实验中学 沈占立

一题三解,各具特色

430223 武汉市光谷实验中学 沈占立

近几年来,武汉市中考题第12题是一道选择题的压轴题,亦是一道多结论判断型问题,题目涉及的知识点多,综合性强,解法灵活多样.兹以武汉市2011年第12题为例予以说明.

如图1,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H.有下列结论：

图1

其中正确的结论有

本题结论①显然成立,结论③也不难得证.很多考生却在结论②上失分较多.本文就此列举三种解法,供读者参考.

1 常规解法——构造全等

证明 延长 GB至K,使BK=DG,连接CK.如图1.∵四边形ABCD是菱形,AB=BD,∴△ABD和△BCD都是等边三角形,∴AD=BD,∠DAE=∠BDF=60°,又∵AE=DF,∴△AED≌△DFB,∴∠ADE=∠DBF,∴∠BGE=∠DBF+∠BDG=∠ADE+∠BDG=∠ADB=60°,∴∠BGD=120°,又∠BCD=60°,∴∠CBG+∠CDG=180°,又∠CBG+∠CBK=180°,∴∠CDG=∠CBK,∴△CDG≌△CBK.∴CG=CK,∠DCG=∠BCK,∴∠GCK=∠DCB=60°,

点评 上述解法不失一般性,虽然解法较繁,但易于理解.

2 标新立异——旋转变换

证明 如图 2所示,将△CDG以点C为旋转中心逆时针旋转60°,得到△CBM,

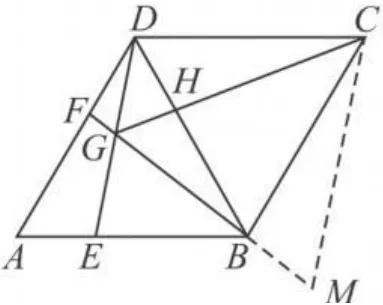
图2

点评 本种解法较简单,也较特殊,颇具创意.

3 巧思妙解——足够地退

证明 当E为AB的中点时,F亦为AD的中点,如图3,

图3

点评 本解法最简单,也最特殊(取E点为特殊点又不失题意),思维发散达到极点.

数学大师华罗庚曾经说过：“善于‘退’,足够地‘退’,退到最原始又不失重要性的地方去研究,是学好数学的一个诀窍！

20110807)