抓住特征,破解“抛物线牵手图形变换”问题
2011-08-25432131湖北省孝感市肖港初中徐金星
432131 湖北省孝感市肖港初中 徐金星
抓住特征,破解“抛物线牵手图形变换”问题
432131 湖北省孝感市肖港初中 徐金星
大家知道,图形变换作为数学课程改革新增的内容,加强对这部分的学习,对学生具有重要的教育价值,有利于发展学生的空间观念.另外,二次函数在初中数学中占有十分重要的地位,所以二次函数的图象和图形变换相结合,综合考查同学们分析、综合、概括、逻辑推理、几何建模以及探究活动的能力,是各级检测中不可多得的好题.本文就以课本中的一道探究题为例,探讨关于这类问题的解法.
课本原题
如图1,在一张纸上作出函数y=x2-2x+3的图象,沿x轴把这张纸对折,描出与抛物线y=x2-2x+3关于x轴对称的抛物线,这条抛物线是哪个二次函数的图象?
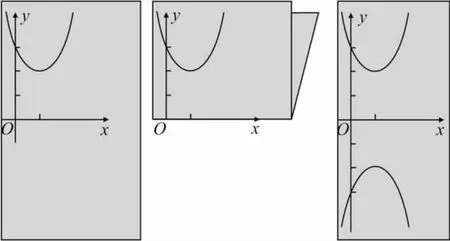
图1
分析 观察描出与抛物线y=x2-2x+3关于x轴对称的抛物线,可以发现这个抛物线的顶点坐标是(1,-2),且过点(0,-3),这样,此抛物线的解析式就可以求出来了.也可以这样想,关于x轴对称的抛物线与原抛物线相比,它开口的方向相反,即向下,而开口大小不变,说明二次项系数为-1.另外,由于对称轴没有变,那么关于x的一次项系数为2.再根据原抛物线与y轴的交点坐标为(0,3),那么其关于x轴对称的点的坐标为(0,-3),这个-3就是新抛物线解析式中的常数项.
解法1 依题意,可知
抛物线y=x2-2x+3关于x轴对称的抛物线的顶点坐标是(1,-2),且过点(0,-3).
设抛物线的解析式为y=a x-( )h2+k(a≠0),则有
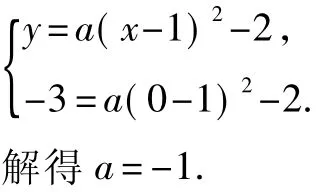
故所求的二次函数的解析式为
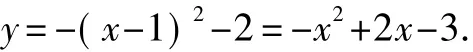
点评 运用这种方法的主要步骤是,首先将原二次函数的解析式配成顶点式,再根据对称找到新抛物线的顶点坐标,最后可以找一个确定的点进行代入(或者根据开口来确定二次项系数).这种方法是解决这类问题的基本方法,它一步步地将所求解析式中的待定系数逐一确定.
解法2 所求的二次函数的解析式为y=ax2+bx+c(a≠0).
观察关于x轴对称的抛物线与原抛物线,对比可知,新抛物线的开口向下,开口大小不变,说明a=-1.
又∵它们的对称轴没有变,
∴b=2.
∵原抛物线与y轴的交点坐标为(0,3),
∴这个交点关于x轴对称的点的坐标为(0,-3),
即c=-3.
故所求的二次函数的解析式为y=-x2+2x-3.
点评 这种方法很明显比第一种方法要抽象得多,虽然表面上看也是将所求解析式中的待定系数逐一确定,在确定这三个待定系数时所运用的是抛物线的性质,这种方法显得简单明了,甚至可以直接看出来.
实际上,对于要确定抛物线关于x轴对称的抛物线的解析式,根据图象性质反映的系数关系,可以得到,抛物线y=ax2+bx+c关于x轴对称的抛物线的解析式为y=-ax2-bx-c.
以上这两种解法都是求图形变换后的抛物线的解析式的很重要的方法,下面将这个问题进行变式,进一步进行探究.
变式1 关于y轴对称
如果将上例中的函数y=x2-2x+3的图象沿y轴对折,那么这条抛物线是哪个二次函数的图象呢?
解析 我们可以寻找抛物线的特征,即抛物线沿y轴翻折后,只改变抛物线的顶点位置,而不改变抛物线的开口方向及大小.这样的话,结合前面所讲的方法就很容易确定了.总结系数之间的关系,实际上就是确定抛物线关于y轴对称的抛物线的解析式.
所以,函数y=x2-2x+3的图象关于y轴对称的抛物线的解析式是y=x2+2x+3.
点评 关于y轴对称可以归纳为:抛物线y=ax2+bx+c关于y轴对称的抛物线的解析式为y=ax2-bx+c.
变式2 关于原点对称
如果在纸上作出上例函数y=x2-2x+3的图象关于原点对称的图象,那么这条抛物线是哪个二次函数的图象呢?
解析 两个关于原点对称的图象,说明这两个图象上的所有点都关于原点对称,而确定抛物线只需要找到顶点和另一个特殊点(如与y轴的交点)的坐标即可.也可以根据性质,从开口、对称轴和与y轴的交点来确定待定系数.
所以,函数y=x2-2x+3的图象关于原点对称的抛物线的解析式是y=-x2-2x-3.
点评 一般地,抛物线y=ax2+bx+c关于原点对称的抛物线的解析式:y=-ax2+bx-c.
变式3 旋转
如果将抛物线y=x2-2x+3绕其顶点旋转180°,求旋转后所得抛物线的解析式.
解 将y=x2-2x+3配成顶点式,得 y=x2-2x+3=(x-1)2+2.
∵旋转前后抛物线的开口方向恰好相反,而开口大小及顶点位置均不变,
∴旋转后所得新抛物线的解析式为y=-(x-1)2+2,即y=-x2+2x+1.
点评 求抛物线y=ax2+bx+c(a≠0)绕其顶点旋转180°后的解析式,同样可先将其配方成顶点式 y=a( x -h)2+k(a≠0),然后将二次项系数直接改变成其相反数即可.
20111008)
