基于纳米压痕技术及有限元模拟的薄膜力学性能研究
2011-08-24戎俊梅柴国钟郝伟娜
戎俊梅,柴国钟,郝伟娜
(浙江工业大学 机械工程学院,浙江 杭州 310032)
基于纳米压痕技术及有限元模拟的薄膜力学性能研究
戎俊梅,柴国钟,郝伟娜
(浙江工业大学 机械工程学院,浙江 杭州 310032)
采用纳米压痕技术结合有限元模拟和量纲分析方法分析薄膜材料的弹塑性性能.用有限元模拟纳米压痕过程,结合量纲分析方法将纳米压痕的加卸载过程与被测材料的力学性能联系起来,建立起两者间的无量纲函数关系结构式,进而结合实际纳米压痕试验所得薄膜的弹性模量和载荷—位移曲线计算出了材料的应力—应变关系.经检验,有限元模拟所得到载荷—位移曲线和纳米压痕试验所得载荷—位移曲线吻合得比较好,因此验证了有限元模型的正确性和材料模拟的正确性.
纳米压痕;有限元模拟;量纲分析;力学性能
随着纳米技术的发展,材料在微纳米尺度下的力学性能逐渐成为人们关注的对象.因此,认识和挖掘薄膜材料的力学性能等基本材料特性成为提高材料性能、寿命和可靠性,以及指导薄膜体系的设计和优化的关键因素.纳米压痕技术作为一种测量薄膜材料力学性能的方法,由于其操作方便、测量及定位分辨率高等特点备受青睐.由于纳米压痕测试技术是建立在压痕问题的弹性解之上的,所以当前的纳米压痕技术只能测量出有限的材料弹性性能,如弹性模量和硬度等.对于微小体积材料的塑性性能,还需结合有限元数值模拟和量纲分析方法来完成的.
1 纳米压痕试验过程
试验样品为在玻璃衬底上沉积氧化锌薄膜,样品表面经机械抛光处理,表面粗糙度为1.4 nm,氧化锌薄膜的厚度为1.3μm.为了排除压痕过程中基底对薄膜的影响,试验中选用压痕深度在130 nm以内.根据文献[1],氧化锌薄膜的应力—应变关系采用双线性强化模型,即

式中:E为材料的弹性模量;σ0,ET分别为材料的屈服强度和塑性切线模量.
运用美国Hysitron公司生产的原位纳米力学测量仪(TriboIndenter)进行纳米压痕试验.该仪器压深分辨率为0.04 nm,载荷分辨率为1 n N.纳米压痕过程包括加载和卸载两个过程,在试验中,加卸载速率均为50μN/s,在最大载荷处保载5 s.每次试验均重复4次,结果取平均值.图1为薄膜在不同载荷下的载荷—位移曲线.图2为薄膜弹性模量E随压痕深度的分布情况.
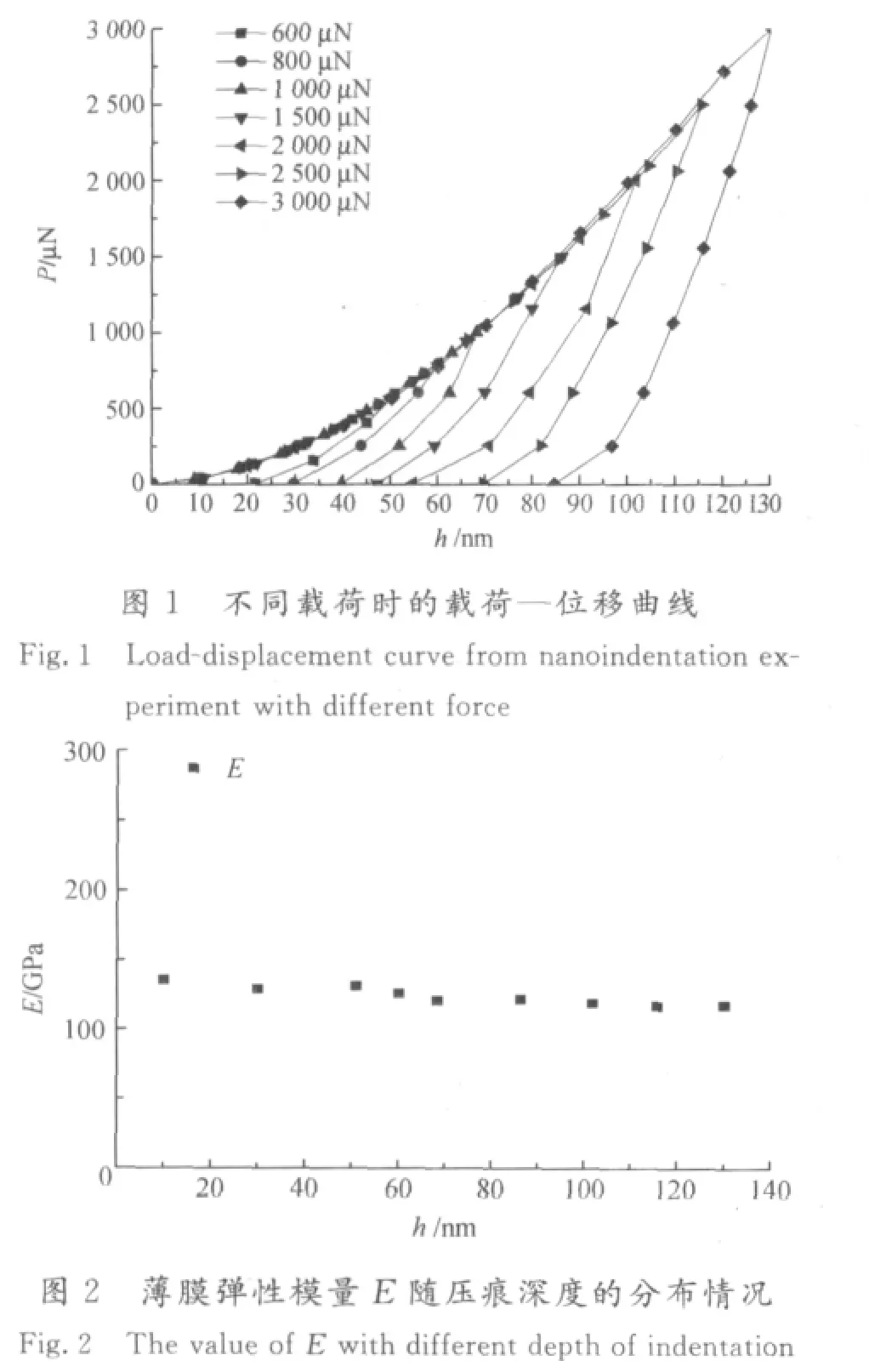
对试验结果取平均值,得出玻璃基底氧化锌薄膜的弹性模量E平均值为130.97 GPa.
2 有限元模拟和量纲分析
2.1 有限元模拟纳米压痕过程及其结果分析
使用ABAQUS有限元软件对压头压入膜/基体系的过程进行模拟.为简化问题,在有限元模型中把Berkovich压头简化为刚体,并用半锥角为70.3°的圆锥压头代替[2];薄膜厚度为1.3μm,基底厚度为8.7μm.薄膜与基底均为均匀、各向同性的材料,并且遵循Von Mises屈服准则及各向同性强化准则.并且根据圣维南原理,在建模时只取局部材料,即模型中的材料尺寸比实际试验中的小,以便减少模型的单元数目,节约计算时间[3].同时考虑到结构和载荷的对称性,为了提高计算效率,仅取膜/基体系的右半部分进行有限元计算.
计算模型中膜/基材料的基本力学参数:氧化锌薄膜的弹性模量为130.97 GPa,泊松比为0.3,玻璃基底的弹性模量为80 GPa,泊松比为0.25,屈服强度为3.2 GPa,应变硬化指数为0.3,其中假设氧化锌薄膜的屈服强度范围为0.1~0.9 GPa,取0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9 GPa,9个确定值,塑性切线模量的范围为15~30 GPa,取15,20,25,30 GPa,4个确定值.这样就构造了氧化锌薄膜的36组参数值.
网格划分采用具有较高计算精度且适用于大应变分析的四节点对称线性减缩积分单元(CAX4R).本模型中共采用了10 609个CAX4R网格,如图3所示.在压头附近采用密网格,远离压头逐渐使用稀疏网格,这样既获得足够的计算精度,又节约计算时间.

图3 薄膜与基底的有限元网格划分Fig.3 The FEM mesh of film and substrate
由于纳米压痕试验被处理为轴对称问题,被测材料沿对称轴的所有节点的水平位移为零,下边界的所有节点的轴向位移也是零,表示材料在一个支撑面上.金刚石压头在有限元分析中被模拟为刚体,在压头上设一个参考点,将整个刚体的约束和位移集中到这个参考点上.分析过程中压头只有向下的一个自由度,加载和卸载过程是时间的线性函数,第一个载荷步在参考点上施加130 nm的向下位移,第二个载荷步将参考点的位移载荷卸载为零.
利用ABAQUS有限元软件模拟计算36组不同力学参数氧化锌薄膜玻璃基底的纳米压痕试验,得出纳米压痕加卸载过程中加载曲率C=P/h2和残余深度hr随塑性切线模量ET和屈服强度σ0的变化情况,如表1,2所示.

表1 不同ET和σ0时C的取值Table 1 The value of C for different ET andσ0 GPa

表2 不同ET和σ0时hr的取值Table 2 The value of hr for different ET andσ0
从表1,2可见:对于氧化锌薄膜/玻璃基底这一膜/基体系,加载曲率C=P/h2以及残余深度hr和塑性切线强度ET以及屈服强度σ0是相关的.
2.2 量纲分析
首先采用Kick模型描述压痕曲线的加载部分[4],即

然后应用П定理[5],确定以下两个无量纲函数表达式

式中:ETf,σ0f为薄膜的塑性切线模量和屈服强度;Es,hr,hm分别为基底的弹性模量、薄膜纳米压痕试验加卸载曲线中的残余位移和最大位移.
2.2.1 无量纲函数Φ的确定
图4为当塑性切线模量ET分别为15,20,25,30 GPa时,无量纲函数Φ随σ0/ES的变化情况.

图4 无量纲函数Φ随E T的变化情况Fig.4 Dimensionless functionΦwith different ET
设图4中四条拟合曲线方程为

根据图4得出A,B的取值见表3.

表3 图4中A,B的取值Table 3 The value of A,B in picture 4
表3中A随ET/ES的变化情况如图5所示.
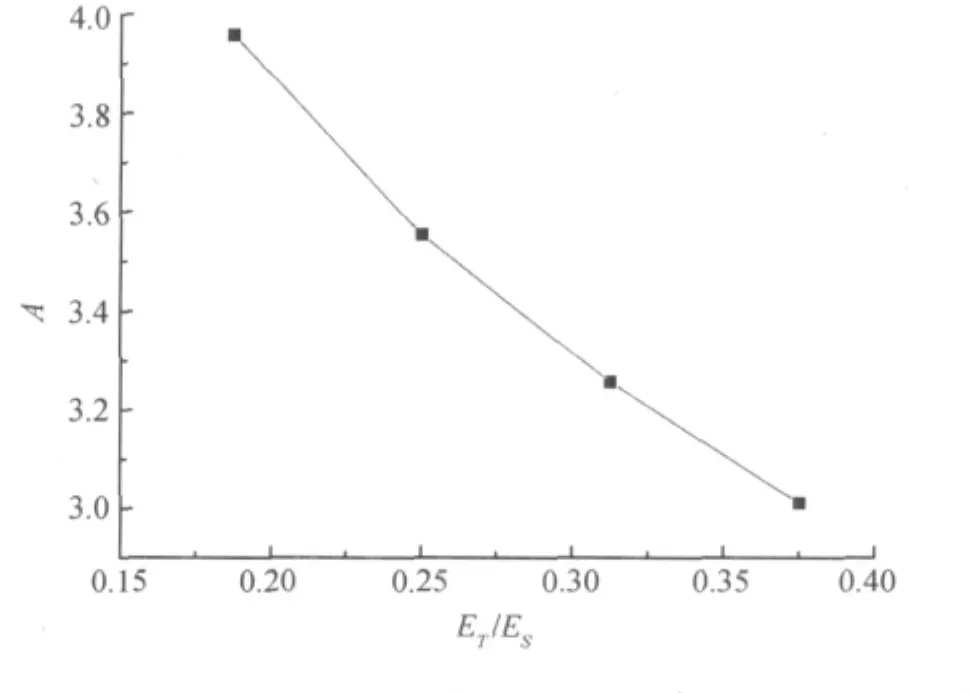
图5 A随E T/ES的变化情况Fig.5 The value of A with different ET/ES
图5中拟合曲线为

表3中B随ET/ES的变化情况如图6所示.

图6 B随E T/ES的变化情况Fig.6 The value of B with different E T/ES
图6中拟合曲线为

综上所述,把式(4,5)代入式(3)可得
2.2.2 无量纲函数Ψ的确定
图7为当塑性切线模量ET分别为15,20,25,30 GPa时,无量纲函数Ψ随σ0/ES的变化情况.
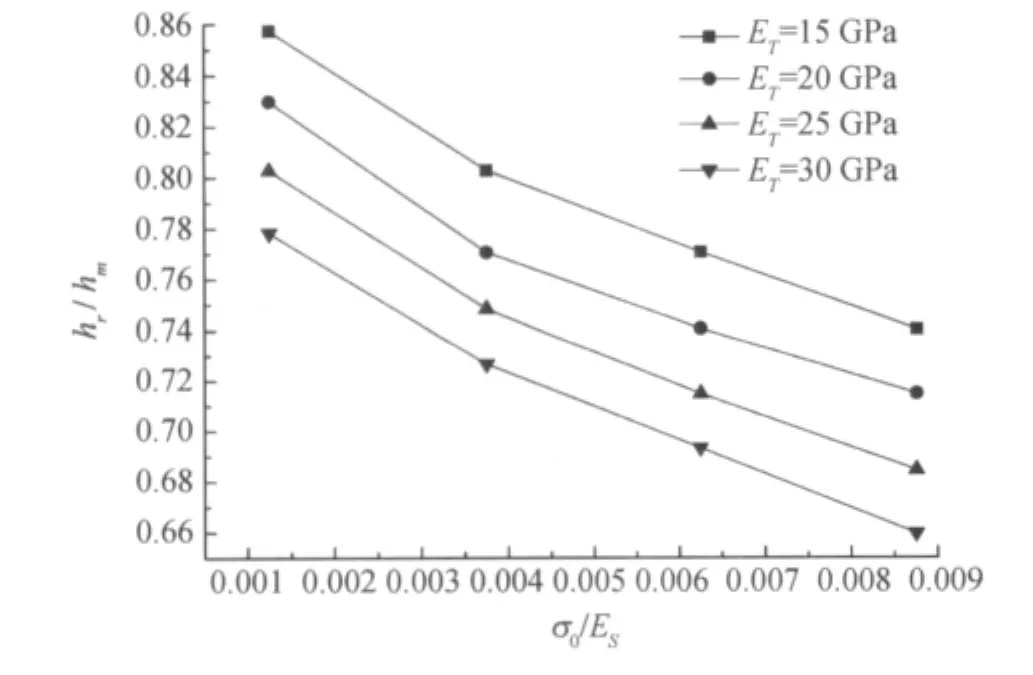
图7 无量纲函数Ψ随E T的变化情况Fig.7 Dimensionless functionΨ with different E T
设图7中四条拟合曲线方程为

根据图7得出A,B的取值见表4.

表4 图7中A,B的取值Table 4 The value of A,B in picture 7
表4中B随ET/ES的变化情况如图8所示.

图8 B随E T/ES的变化情况Fig.8 The value of B with different ET/ES
图8中拟合曲线为

综上所述,把值A和式(8)代入式(7)可得

3 屈服强度和塑性切线模量的确定
在纳米压痕试验中,设定最大压入深度为130 nm.图9为最大压入深度为130 nm时的载荷—位移曲线图.

图9 压痕深度为130 nm时的载荷—位移曲线Fig.9 Load-displacement curve of ZnO film with 130 nm depth of indentation
图9中,通过ORIGIN软件可得加载曲率C=P/h2=150 GPa,残余深度与最大压痕深度之比hr/hm=0.654.把C=P/h2=150 GPa,hr/hm=0.654代入方程式(6,9)中,即

通过解方程式(10,11),可得ET=11.56 GPa,σ0=2.341 GPa.
由此可得氧化锌薄膜的应力—应变关系为

其相应的应力—应变曲线如图10所示.
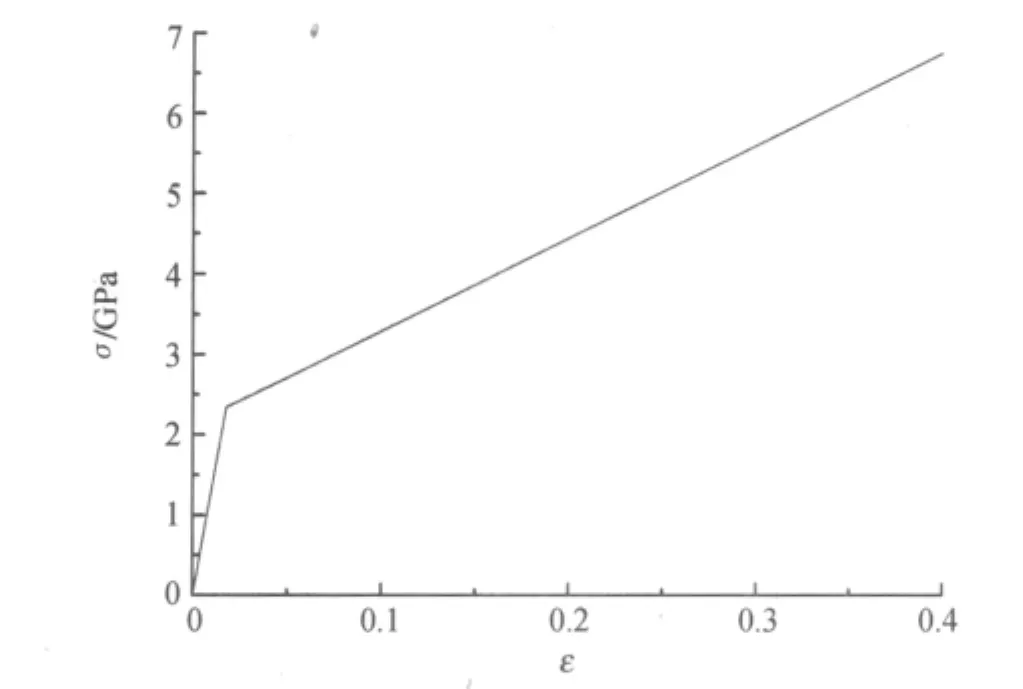
图10 氧化锌薄膜的应力—应变关系Fig.10 Theσ-εcurve of the ZnO film
把计算所得氧化锌薄膜的应力—应变关系输入有限元模型,重新计算薄膜的载荷—位移曲线.图11为有限元模拟计算所得载荷—位移曲线和纳米压痕试验所得载荷—位移曲线的比较,可以发现两者吻合的比较好.

图11 有限元模拟和纳米压痕试验载荷—位移曲线的比较ig.11 The P—h curves of the FEM and nanoindentation
4 结 论
通过纳米压痕试验测得玻璃基底氧化锌薄膜的载荷—位移曲线和弹性模量,结合量纲分析和有限元方法计算出氧化锌薄膜的应力—应变关系.将有限元模拟和纳米压痕试验所得载荷—位移曲线进行比较,发现两者吻合得比较好.因此,这种得到材料弹塑性性能的方法是正确可行的.
[1]PELLETIER H.Predictive model to estimate the stress-strain curves of bulk metals using nanoindentation[J].Tribology International,2006,39:593-606.
[2]BRESSAN J D,TRANMONTIN A,ROSA C.Modeling of nanoindentation of bulk and thin film by finite element method[J].Wear,2005,258:115-122.
[3]BOUZAKIS K D,MICHAILIDS N.Coating elastic-plastic properties determined by means of nanoindentations and FEM-supported evaluation algorithms[J].Thin Solid Films,2004,469/470:227-232.
[4]DAO M,CHOLLACOOP N,VANVLIET K J,et al.Computational modeling of the forward and reverse problems in instrumented sharp indentation[J].Acta Mater,2001(49):3899-3918.
[5]谈庆明.量纲分析[M].合肥:中国科学技术大学出版社,2005.
[6]BENNY P.A critical appraisal of nanoindentation with application to elastic-plastic solids and soft materials[D].Pasadena:California Institute of Technology,2009.
[7]CAO Y P,LU J.A new method to extract the plastic properties of metal materials from an instrumented spherical indentation loading curve[J].Acta Mater,2004(52):4023-4032.
[8]LIN Jiang,NIU Xiao-yang,SHU Xue-feng.Reverse analysis for determining the mechanical properties of zeolite ferrierite crystal[J].Journal of Nanomaterials,2008(77):1-7.
[9]LIU Y,WANG B,YOSHINO M,et al.Combined numerical simulation and nanoindentation for determining mechanical properties of single crystal copper at mesoscale[J].Journal of the Mechanics and Physics of Solids,2005,53(12):2718-2741.
Research on mechanical properties of film based on nano-indentation technology and finite element simulation
RONG Jun-mei,CHAI Guo-zhong,HAO Wei-na
(College of Mechanical Engineering,Zhejiang University of Technology,Hangzhou 310032,China)
A method of determining mechanical properties of thin films was developed by combining nano-indentation with finite element method and dimensional analysis.The simulations of indentation process were performed as a first step.The dimensional analysis was then applied to derive the relationship between indentation and mechanical properties of material.Furthermore,the stress-strain curve was figured out,according to the real Load-Depth curves and the value of E got in the nano-indentation experiments and the dimensionless functions.Finally,the Load-displacement curve by the FEM was compared with the actual Loaddisplacement curve of the nano-indentation.A good correlation was demonstrated and the validity of the proposed method was therefore proved.
nano-indentation;finite element method;dimensional analysis;mechanical properties
TH140.7
A
1006-4303(2011)06-0674-05
2010-09-27
戎俊梅(1986—),女,山西忻州人,硕士研究生,研究方向为计算机辅助设计及制造,E-mail:rjm1986@yahoo.cn.通信作者:柴国钟教授,E-mail:chaigz@zjut.edu.cn.
(
陈石平)
