基于模糊推理系统的作业车间交货期瓶颈辨识研究

顾余容，鲁建厦，詹 燕

（浙江工业大学 机械工程学院，浙江 杭州 310032）

基于模糊推理系统的作业车间交货期瓶颈辨识研究

顾余容，鲁建厦，詹 燕

（浙江工业大学 机械工程学院，浙江 杭州 310032）

针对现今制造企业的客户交货期满意度低的问题，阐述了研究交货期瓶颈问题的重要性和紧迫性.通过应用模糊推理系统知识来定义交货期瓶颈，提出了辨识不同加工阶段的交货期瓶颈工件的方法，建立了作业车间生产系统的交货期瓶颈辨识模型.基于模糊推理系统的辨识方法操作方便，便于用计算机软件实现.最后，应用某加工车间的实例说明了该辨识方法的有效性.

瓶颈辨识；交货期瓶颈；模糊推理系统；作业车间

瓶颈辨识是企业生产瓶颈管理和控制的基础，现今以约束理论（TOC）提出的瓶颈定义和瓶颈辨识方法使用较为广泛，但对于企业生产系统研究来说过于笼统，无法全面反映实际需要［1］.而随着市场竞争日益激烈，客户越来越要求产品个性化和多样化，客户对交货时间的要求也越来越严格，以及市场需求的不确定性，生产系统往往不能满足客户的交货期的要求.由于客户的严格交货日期要求和超负荷的生产任务，使在交货期限内要求安排加工的工件所需要的机器加工时间超出了实际能提供的机器时间，从而产生了交货期瓶颈，交货期瓶颈问题成为瓶颈管理与控制中一个突出的问题.

目前对交货期瓶颈相关的研究文献并不多，Meerkov S.M提出用灵敏度分析法来定义和识别系统的交货期瓶颈：针对系统预定交货期的表现指标，分析系统内每个机器的加工情况对系统整体表现的影响，灵敏度越高的机器越容易成为系统的瓶颈［2－4］.吴春辉提出采用资源负荷状态图、负荷状态曲线、数学表达式来表示各机器交货时间瓶颈的分布［5］.以上研究提出的瓶颈定义及其辨识技术与TOC提出的瓶颈定义及辨识方法相比目标更为明确，且考虑更加全面，但仍存在模型复杂、操作不便和外生约束多等不足之处［6］.而模糊推理系统具有不依赖于对象的精确数学模型，易于操作及鲁棒性好等优点，因此，采用模糊推理系统的知识来定义和识别交货期瓶颈，建立作业车间生产系统的交货期瓶颈辨识模型.

1 模糊推理系统的推理步骤及类型选择

模糊推理系统（fuzzy inference system，FIS）是建立在模糊集合论，模糊IF-THEN规则和模糊推理等概念基础上的先进计算框架.它在诸如自动控制、数据分类、决策分析、专家系统、时间序列预测、机器人和模式识别等众多领域中得到了成功的应用［7］.

1.1 模糊推理系统的推理步骤

模糊推理系统依据模糊IF-THEN规则进行推理的步骤［8］如下：

（1）将输入变量带入隶属度函数中，求出该输入变量的每一个语言值对应的隶属度值，这一步称作模糊化.

（2）通过对隶属度值进行计算（通常为乘、取最小值），可求得各条规则的激励强度.

（3）依据每条规则的激励强度求出每条规则的输出（模糊值或精确值）.

（4）将模糊推理得到的结果转换为精确值，这一步称为去模糊化.

笔者将按照上述推理的步骤从而来确定交货期瓶颈.

1.2 Mamdani型模糊推理系统

最常见的模糊推理系统有3类：纯模糊逻辑系统、高木－关野（Takagi-Sugeno）型和迈达尼（Mamdani）型.由于 Mamdani型模糊推理的规则形式更符合人们思维和语言表达的习惯，因此采用Mamdani型模糊推理系统来确定作业车间的交货期瓶颈.Mamdani型模糊推理算法如下：

Mamdani型模糊推理算法采用极小运算规则定义模糊蕴含表达的模糊关系［9］，如规则：

式中：x为输入语言变量；A为推理前件的模糊集合；y为输出语言变量；B为模糊规则的后件.用RC表示模糊关系：

2 作业车间交货期瓶颈辨识建模

2.1 作业车间初调度的启发式算法设计

在定义交货期瓶颈前，首先需要设计一个启发式算法来对作业车间进行初步调度.该算法的具体步骤如下：

假设n个加工工件｛Ji｝ni＝1按给定的工艺路径依次在｛Mk｝mk＝1台机器上加工，pj为工序j的加工时间，di为工件i的交货期限，wi为工件权重（表示工件的误工费用或客户的重要程度等），它们是固定已知的（这里不考虑加工批量问题）.则松弛指数θi定义为

式中：∑j∈Jipj为工件i的各工序加工时间总和.

最终将所有的工序按照优先指数αi的大小进行递减排序，并且按照这个排序规则将各工序分配到它们相应的加工机器上，从而可得到一个初始的调度结果，以获得各工序所安排的完成时间.

2.2 基于模糊推理系统的交货期瓶颈工件的确定和表示

在生产系统中，瓶颈可以是加工机器或被加工的工件.为制定有效的生产计划，管理者不仅仅希望确定整个生产系统的瓶颈，同时也希望知道各个加工阶段的瓶颈.因而在作业车间中，对于同一加工阶段（即各个工件先后经过同一机器加工），对按时交货影响最大的Job，可认为是该加工阶段的交货期瓶颈.可应用模糊推理系统来计算交货期瓶颈工件指标值（JBN），从而来确定各加工阶段的交货期瓶颈工件（due-time bottleneck job，DBJ）.

在设计模糊控制器（在模糊系统中用作控制器的模糊推理系统）之前，首先需要定义以下三个变量：

（1）工件i的相对拖期gi：

式中：di和Fi分别为工件i的交货期和当前排序下该工件的完工时间.

（2）工件i的相对松弛时间hi：

（3）工件i的标准化权重vi：

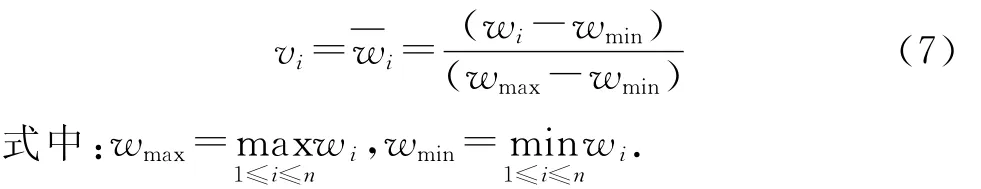
基于以上设定的三个变量，设计以下一个模糊控制器来计算JBN的值.

2.2.1 定义输入／输出变量

此模糊控制器将gi，hi和vi设定为输入变量，为每个工件所定义的JBN值为输出变量.在模糊推理系统中，这四个输入／输出语言变量分别由G，H，V和B来表示，并被划分成以下三个模糊集合：

G，H＝｛负数（NL），大约是零（Z），正数（PL）｝.

V＝｛小（S），中（M），大（L）｝.

B＝｛不是瓶颈工件（NB），可能是瓶颈工件（MB），是瓶颈工件（B）｝.

2.2.2 定义隶属函数

在此模糊控制器中，所有隶属函数都选用对称三角形，因而只需确定首末两个点，便能确定该隶属函数的表达式.例如，上述的一个语言变量描述为｛（－∞，a，b）；（b，c）；（c，d，＋∞）｝，则其相应的三个隶属函数如图1所示.

图1 模糊控制器采用的隶属函数Fig.1 The membership functions adopted by the fuzzy controller

2.2.3 建立模糊规则

交货期瓶颈工件是在生产调度优化过程中需要优先考虑的工件，因为它对提高整个系统的交货期满意度及产出效绩扮演着重要的角色.而在实际的作业车间调度中，存在着某些人类经验能够判断在不同的环境情况下，哪类工件具有优先权.经过进一步的提炼，这些经验知识可描述为多条模糊IFTHEN规则.例如，“If G＝PL，H＝NL and V＝L，then B＝B”表示在当前调度下，具有较大的相对拖期和相对松弛时间，较大权重的工件可认为是交货期瓶颈工件.

依据上述的这些原则，可得到包含所有输入变量可行组合的模糊规则表1.这些规则从各个不同方面反映了交货期瓶颈工件的基本特征.

表1 模糊规则表Table 1 The fuzzy rule table

2.2.4 选择模糊推理类型和解模糊化

基于上述18个模糊规则的模糊推理系统将采用Mamdani型，其中t－范数采用“min”算子.为使最后输出的模糊量清晰化，则采用最大隶属度最小值法（SOM）作为解模糊的方法.例如，输出结果ZSOM表示使模糊量μA（z）极大化的z的最小值（在幅值意义下）.

通过采用上述所设计的模糊推理系统，将能得到在初始调度后，每个工件的交货期瓶颈指标值.而且从设定的条件可知，所指定的加工阶段不同，所得的JBN值也不同.因而，不同的加工阶段有不同的交货期瓶颈，即具有最大JBN值的工件即为当前加工阶段的交货期瓶颈工件（DBJ）.

3 实例仿真

以某制造业加工车间为例，将生产数据做了简化处理，设计了一个由5个工件在5台机器上完成加工任务的仿真实例.该加工车间加工5类典型零件，每类零件需要分别在机器完成冲、刨、车、钻、铣加工，每类零件的工艺路线不同，表2为工件加工信息.

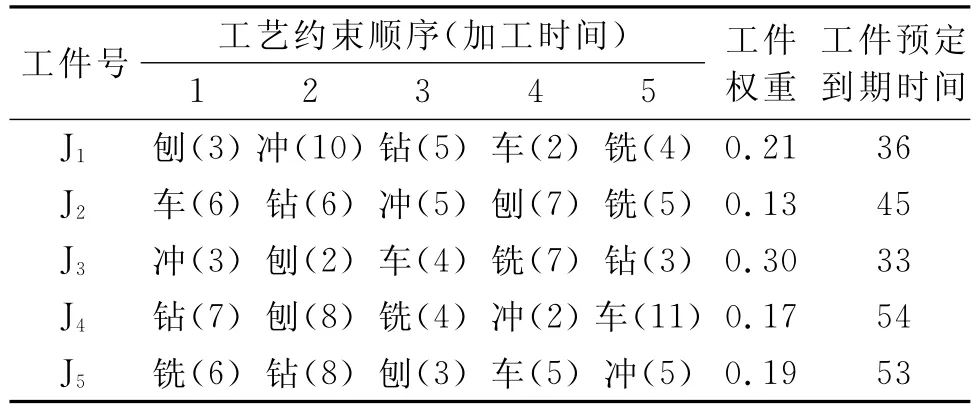
表2 工件加工信息表Table 2 Workpieces task information

根据表2的数据，采用上述设计的启发式算法，可得各道工序的优先指数α，从而得到该作业车间一个初始的调度结果，如图2所示.

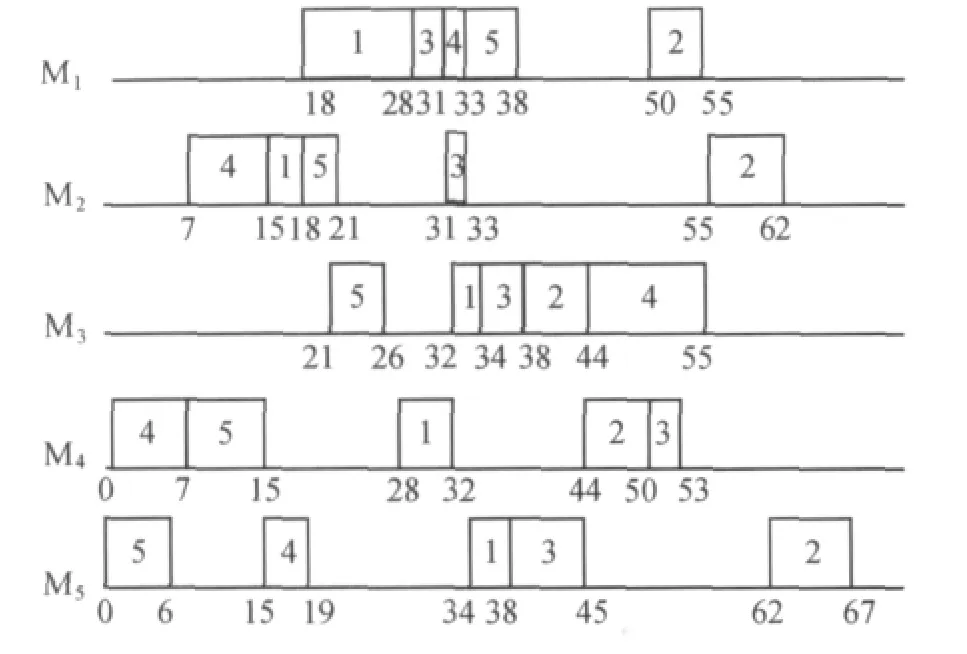
图2 初始调度甘特图Fig.2 Gantt chart of initial scheduling

然后，在Pentium4，CPU 主频2.80 GHz，1.2 GB内存和WindowsXP操作系统下，利用Matlab7.1中的模糊逻辑工具箱（Fuzzy logic Toolbox）实现上述设计的模糊推理系统，其中四个变量G，H，V和B的隶属函数分别设定为｛（－1，－0.3）；（－0.3，0.3）；（0.3，1，＋∞）｝，｛（－∞，－1，－0.3）；（－0.3，0.3）；（0.3，1）｝，｛（0.1，0.3）；（0.3，0.7）；（0.7，1）｝和｛（0，0.2）；（0.2，0.7）；（0.7，1）｝.表3为仿真分析结果.

表3 仿真分析结果Table 3 Simulation result analysis

由上述仿真分析结果可知，工件J1在所有的加工阶段（即分别是在机器 M1，M2，M3，M4和 M5上的加工阶段）都具有最大的交货期瓶颈指标值，则对于该作业车间来说，对基于交货期的生产目标影响最大的交货期瓶颈都是工件J1.因此，在该作业车间后续的调度工作中，应考虑工件J1在各个加工阶段的优先加工权.

4 结 论

针对现今所研究的交货期瓶颈模型的复杂性，辨识方法的操作不便性等缺点，提出采用模糊推理系统的知识来定义和识别交货期瓶颈，建立作业车间生产系统的交货期瓶颈辨识模型.该模糊推理系统是由人对交货期瓶颈的某种经验为依据而设计，因而辨识方法不依赖与瓶颈本身的精确模型，易于被操作人员接受，便于用计算机软件实现.应用某加工车间的实例说明了辨识方法的有效性.该方法为作业车间生产调度中瓶颈管理和控制提供了理论依据.

［1］周云霞，刘敏.生产物流中的瓶颈辨识研究［J］.物流科技，2005，28（8）：11-15.

［2］MOSS H K.Toward the estimation of bottleneck shiftiness in a manufacturing operation［J］.Production and Inventory Management Journal，1999，40（2）：53-58.

［2］KUO C T，LIM J T，MEERKOV S M.Bottlenecks in serial production lines：a system-theoretic approach［J］.Mathematical Problems in Engineering，1996（2）：233-276.

［3］LI Jing-shan，MEERKOV S M.Bottlenecks with respect to due-time performance in pull serial production lines［J］.Mathematical Problems in Engineering，2000（5）：479-498.

［4］CHIANG S Y，KUO C T，MEERKOV S M.C-bottlenecks in serial production lines：identification and application［J］.Mathematical Problems in Engineering，2001，7（6）：543-578.

［5］吴春辉.基于瓶颈分析的成套订单调度算法研究［D］.武汉：华中科技大学，2006.

［6］沈妙妙.基于约束理论的生产系统瓶颈辨识及转移性研究［D］.杭州：浙江工业大学，2006.

［7］倪春木.一种新型的模糊推理系统及状态预测逆控制［D］.厦门：厦门大学，2001.

［8］尹海娥.基于模糊推理系统的自适应噪声消除方法在视觉诱发脑电信号提取中的应用［D］.北京：北京工业大学，2003.

［9］钟飞，钟毓宁.Mamdani与Sugeno型模糊推理的应用研究［J］.湖北工业大学学报，2005，20（2）：28-30.

［10］JAIN A S，MEERAN S.Deterministic job-shop scheduling：past，present，and future［J］.European Journal of Operation Research，1999，113（2）：390-434.

Study on due-time bottleneck identification in job shop based on fuzzy inference system

GU Yu-rong，LU Jian-sha，ZHAN Yan
（College of Mechanical Engineering，Zhejiang University of Technology，Hangzhou 310032，China）

Aiming at the rising problem of poor due-time satisfaction in current manufacturing industry，the importance and urgency of the study on due-time bottleneck is described.A fuzzy inference system is employed to define due-time bottleneck.The identification method of due-time bottleneck job in different processing stage is proposed and the identification model of due-time bottleneck in job shop is established.The identification method based on fuzzy inference system is convenient to be practically applied and also suitable to be employed to simulate by computer software.The example concerning a workshop proves the feasibility of the model and method.

bottleneck identification；due-tine bottleneck；fuzzy inference system；job shop

TP301

A

1006-4303（2011）06-0670-04

2010-09-28

国家自然科学基金项目（70971118）；浙江省科技厅计划项目（2009C31025，2009C11164）

顾余容（1987—），女，浙江宁波人，硕士研究生，研究方向为精益生产、约束理论，E-mail：shixialing123＠126.com.

（

陈石平）