基于几何精度衰减因子的单站无源定位精度分析方法
2011-08-21陈思剑
陈思剑,张 旻,罗 争
(1.解放军电子工程学院,安徽 合肥 230037;2.安徽省电子制约技术重点实验室,安徽 合肥 230037)
0 引言
单站无源定位技术是电子对抗应用中的一项重要技术,不仅定位系统设备量小,独立性强,而且较其他无源定位系统具有更好的战术灵活性、隐蔽性和不易被敌方发觉的优点,对提高系统在电子战环境下的生存和作战能力有着极其重要的作用和意义[1-4]。无源定位系统模型讨论了观测站利用什么观测量来实现对辐射源无源定位的问题;定位算法则是研究如何利用上述模型完成定位。然而,上述的定位模型和定位算法能否应用于工程实际中,必须通过定位精度分析进行评估,即定位精度分析对定位算法的最终选择具有决定性的意义。测量TDOA是一种单站无源定位方法,具有较高的研究价值。文献[5—6]中研究了到达方向(DOA)和到达时间(TOA)对运动辐射源单站无源定位的模型和算法,可以实现固定单站对运动辐射源的定位,但是目前尚未有文献对其定位精度进行专门的研究分析,这便使得该定位方法是否能够满足下一步工程应用的定位精度要求变得无据可循。
为了验证测量TDOA定位方法是否能满足工程应用定位精度要求,本文提出一种基于几何精度衰减因子(GDOP)的单站无源定位精度分析方法。
1 基于TDOA固定单站的定位原理
根据文献[7]中提出的TDOA固定单站无源定位方法,得到本文的定位方法总体思路:首先建立定位模型,然后利用对辐射源飞行目标测量得到的数据信息,通过分析观测平台和目标间的运动关系,从运动学原理的角度出发,根据现有的几何知识,求解出目标的位置信息,最后对定位解进行单次和多次的定位精度仿真分析,得出相应结论。论文中定位方法研究的基本原理如图1所示,虚线框图是本文的重点。

图1 单站无源定位技术的基本原理图Fig.1 The basic schematic of single observer passive location
从文献[7]中可知,在没有误差的情况下,通过三次DOA和四次TOA的测量数据可以对辐射源目标进行精确定位。为了易于表述,本文以二维情况为例讨论,三维条件可以用同样的方法分析。假定观测站O固定不动,设对周期Tr的全部脉冲列,每隔M个脉冲到达时间测量时刻为Tj(j=0,1,2,3…),MTr时间内目标运动的距离为d,且Tj时刻的观测方位角为βj,如图2所示。

图2 辐射源与观测位置的运动几何关系模型Fig.2 The geometry relation diagram of emitter and observer position


式(3)中,c为电磁波传播速度,且Δrj=rj-rj-1。
对于匀速直线运动目标,只要航迹不是径向,即Δβj=0,航向角有解。根据三次DOA和四次TOA的测量数据,通过三角形的几何关系分别可求解出航向角θ、距离r、d和速度v的表达式如下:
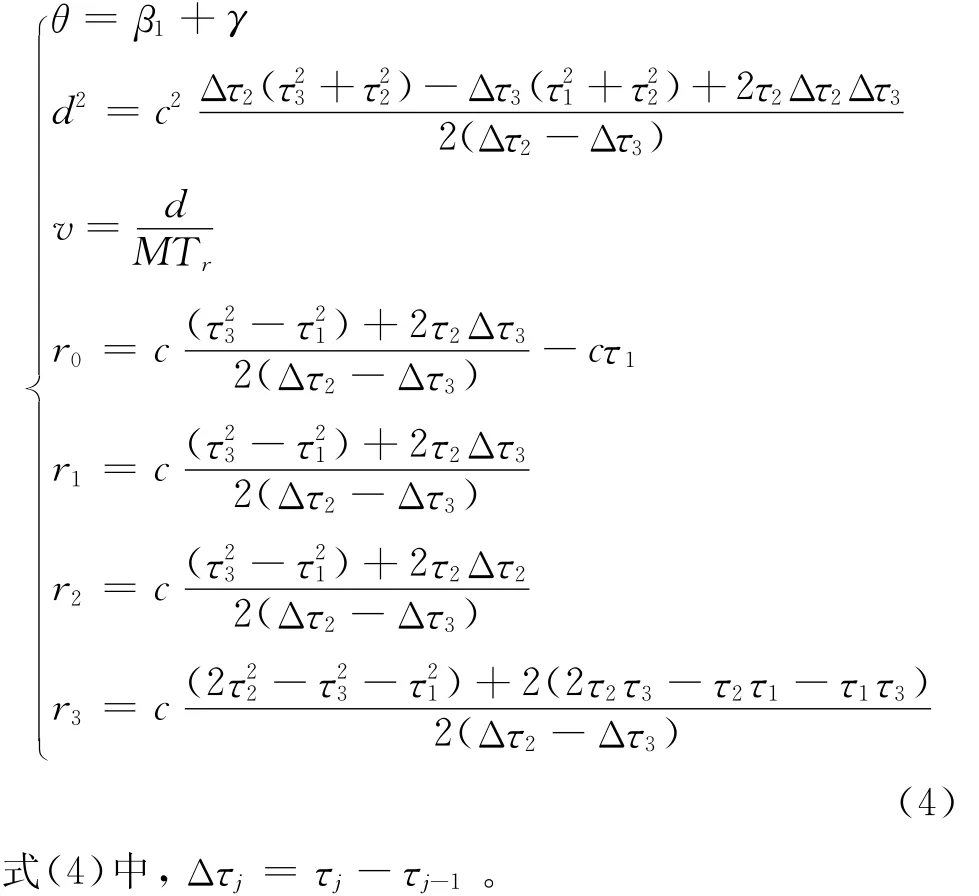
通过上述TDOA基本原理的表达式,可以看出DOA和TOA等参数的测量误差对定位结果会产生相应的影响,但是无法知道对其定位精度影响的具体程度。所以,本文提出了一种基于GDOP的定位精度分析方法,很好地解决了该问题。
2 TD-G定位精度分析方法原理
在第1节中,对图2中基于TDOA固定单站对匀速直线辐射源目标无源定位的二维模型进行分析,可以得到了r、v、DOA、TOA之间的关系,但是要确定该定位方法的实用价值,就必须进行深入研究。因此,针对各参数的测量误差对定位结果影响程度是否能够满足该定位方法工程应用要求的问题,本文提出了一种基于GDOP的定位精度分析方法,该分析方法是在测量TOA和DOA的基础上,以GDOP的推导为出发点进行深入研究,故将其简称为TD-G定位精度分析方法。
2.1 几何精度衰减因子(GDOP)
如图2,已知条件与第1章中的基本相同,并设(xS,yS)为目标S的位置,(x0,y0)为观测站O 在坐标系中的位置,S0为初始观测到达时间,r0为初始S、O之间的距离,c为电磁波传播速度,利用固定单站无源定位方法对匀速直线飞行的目标进行定位的表达式可整理为:

式(5)中:

假设获得的测量参数均值为零且相互独立,且均方值分别为:

为了研究具体影响的程度,对式(6)全微分可得目标位置的定位均方误差如下

则定位误差为

2.2 TD-G定位精度分析方法
在2.1节中,对式(5)左边含有XS的等式进行分析发现,等式右边分别有X0、Tn、n MTr、r0和βn五个可变测量参数。容易看出,在参数测量误差确定后,n可以在0~3之间随机取值;X0的测量误差对定位结果影响较小;从式(4)中可知,r0的测量误差取决于ΔT的测量误差,它对定位精度的影响间接通过σr的大小反应出来,见式(8)。对含有YS的等式分析方法与XS相同。
从式(8)中可以看出,在两个等式右边的四个误差项当中,σβ和σT两个误差项的系数中包含c2,这极大地影响了定位均方误差的结果;而由于量级的原因,另外两项的测量误差变化对结果的影响几乎可以忽略不计。所以,包含有σβ和σT的两项重要参数的变化对等式左边的结果影响占主导地位,进而影响了定位误差GDOP的大小。
TD-G定位精度分析方法步骤如下:
1)在无测量误差的条件下,验证测量TDOA固定单站无源定位方法的可实现性。
2)利用本文推导的GDOP的结果进行单次定位误差分析,来判断对定位精度起主导影响作用的测量因子,并确定其可观测区域。
3)根据DOA和TOA参数的实际测量误差范围,计算定位点的均方根误差和相对定位误差。利用三组不同的测量误差数据研究该定位方法得到的结果是否达到工程应用的精度要求。
4)最后分别对该定位方法随着DOA和TOA参数的测量误差线性变化的相应变化结果进行研究,即根据求出的一系列相对定位误差结果对定位的稳定性进行判断。
经过上述步骤分析之后,该定位方法在工程中的适用性和定位的稳定性便可以清楚地知道,这就是TD-G定位精度分析方法的优势所在。下面通过实验仿真来研究该分析方法的实用性。
3 计算机的仿真与分析
3.1 实验1无测量误差的条件下固定单站(GDOP)无源定位的仿真分析
如图2所示,已知观测站O位于坐标原点,目标做匀速直线运动,飞行速度v=240 m/s,飞行航向角θ=150°,运动的初始位置为(9 000,9 000)m,初始方位角为45°,辐射源发射的脉冲信号周期为Tr=2.5 ms,采样脉冲数为M =1 000,在等MTr时间内目标运动的距离AB=BC=CD=d。设在Tj时刻的观测方位角为βj(j=0,1,2,3),图3则为相关仿真图。



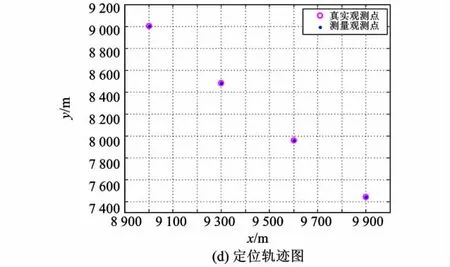
图3 利用DOA和TOA的测量数据的定位结果Fig.3 The location results using DOA and TOA measurements
结论:通过仿真结果可以发现,在没有误差干扰的情况下,真实定位值和测量值完全一致,从而,验证了在固定单观测站对匀速直线运动的辐射源目标无源定位的条件下,利用DOA和TOA的测量数据,可以精确定位。
3.2 实验2单次定位误差的仿真分析
基本仿真条件和目标的运动轨迹与实验1相同,另外,设标准的DOA测量误差、TOA测量误差、观测站址各分量的误差和测距误差分别为σβ=2.5 mrad,σT=12 ns,σw=5 m,σr=50 m,n=1。
根据前文推导的定位误差公式,基于测量子集(T,β)的定位误差等高线分布对比仿真结果如图4所示。

图4 基于单站无源定位TDOA测量的定位误差等高线Fig.4 The location error contour mapping based on single observer passive location using TDOA measurements
从仿真结果可得到如下结论:
1)在400 k m×400 k m的区域内,定位误差基本都在3 k m以内,可以满足工程应用定位精度要求。从仿真图的定位误差结果可知:在影响单次定位精度的因素中,DOA和TOA测量精度起着主导作用。
2)飞行器和目标间的相对运动关系对定位精度也存在影响。沿目标运动速度方向的定位误差越大,可能出现不可观测的情况[8];在与目标运动速度方向垂直的方向上测距误差最小。
3.3 实验3对比DOA、TOA测量误差对定位精度的影响
用三组不同的DOA和TOA测量误差对实验1中的四个定位点进行定位精度分析,分别对各点进行500次蒙特卡罗仿真。仿真条件和目标的运动轨迹与实验2相同,仿真结果如表1所示。

表1 不同DOA和TOA测量精度条件下的定位精度对比Tab.1 The location precision co mparison accor ding to different DOA and TOA measurements
在表1中,可知目标的真实位置和在三组不同的DOA和TOA测量误差条件下的定位结果,对比发现:1)受测量条件的影响,目标位置与真实位置点之间总会存在一定的偏差;2)从表中的第1和第2种情况对比可以看出,在测时差精度为12 ns的情况下,随着DOA测量精度从2.5 mrad变化为5 mrad,定位精度基本不变;而第1和第3种情况对比可知,在DOA测量精度不变的情况下,随着TOA的测量精度从12 ns变化为24 ns,四个定位点的平均均方根定位误差变化较大,增大了近1倍。在工程应用中,上述的DOA和TOA测量技术已经很成熟。因而,TOA的测量精度成为影响定位精度的主导因素之一,即该定位方法对TOA的测量精度具有较高的要求。3)由表1可以得知,经过500次蒙特卡洛仿真,四个定位点的相对定位精度依然可以稳定在2% 以内,足以说明该定位方法具有较高的定位精度,因此,该定位方法具有比较高的实用性,可以进行更深地研究。
3.4 实验4单定位点多次定位误差的仿真分析
从实验3中的结论可知,四个定位点的定位精度基本一致。为了更进一步研究DOA和TOA的测量精度对定位精度的影响,下列实验观察上述四个定位点的相对定位误差分别随着DOA测量精度和TOA测量精度变化而变化的具体情况,并随机抽取一个定位点进行定位精度仿真实验,假设DOA测量误差范围为0~40 mrad,步进为1 mrad;TOA测量误差范围为0~40 ns,步进为1 ns,仿真条件和目标运动轨迹与实验3相同,仿真结果取500次Monte-Carlo。仿真结果如图5、图6所示。原始DOA测量精度σβ=2.5 mrad,TOA测量精度σT=12 ns。且该结果用相对定位误差

式(10)中,(xk,yk)和)为目标在上述四个定位点中随机选取的第k个定位点的位置的真实值和测量值,rk为k时刻目标与固定单观测站之间的距离,δrk则为各方向上的误差平方和。
从图5中可以看出,在TOA测量精度σT=12 ns不变的条件下,随着DOA的测量精度从0 mrad逐渐增大到40 mrad,相对定位误差从2.5%增加到3.5%,增长趋势比较平缓;而从图6中可知,在DOA测量精度σβ恒为2.5 mrad的条件下,随着TOA的测量精度从0 ns逐渐增大到40 ns,相对定位误差从0.2%增大到4.3%。所以,相比较而言,TOA的测量精度对定位精度的影响更大。另外,对于随机选取的定位点,在DOA测量精度增大到40 mrad或TOA测量精度增大到40 ns的情况下,相对定位精度依然可以保持在4.3%以内,足以说明该方法具备了工程应用的精度要求,且具有较好的定位稳定性,体现了其良好的实际应用价值。

图5 DOA测量误差对定位精度的影响Fig.5 The location precision influence based on DOA error

图6 TOA测量误差对定位精度的影响Fig.6 The location precision influence based on TOA error
4 结论
本文提出了一种基于几何精度衰减因子(GDOP)的定位精度分析方法。该方法首先提取了影响TDOA定位精度的测量因子;然后分别以这些因子作为输入变量,根据几何精度衰减因子(GDOP),得到了相对定位误差与影响定位结果的参数测量误差之间的变化关系以及可观测区域;最后再确定是否能够满足具体工程项目的定位精度和定位稳定性标准。仿真结果表明:该定位精度分析方法能够全面地评估TDOA的应用价值,具有重要的意义,经该方法验证,TDOA具有较高的定位精度和较好的定位稳定性,可以满足工程应用的实际定位要求,并具有较强的实用性。论文中的研究内容和结论为该方法下一步在工程中的应用提供了可靠的适用依据,同时也填补了相关理论空缺,对其他无源定位方法的精度分析也具有一定借鉴作用。
[1]Ying W D.Constrained total least squares algorit h m f or passive location based on bearing-only measurements[J].Science in China Series F:Infor mation Sciences,2007,50(4):576-586.
[2]孙仲康,周一宇,何黎星.单多基地有源无源定位技术[M].北京:国防工业出版社,1996.
[3]Song T L.Observability of target tracking with bearingonly measurements[J].IEEE Transaction on Aerospace and Electronic System,1996,33(4):1 468-1 472.
[4]李宗华,郭福成,周一宇,等.测量TOA和DOA的单站无源定位跟踪可观测条件[J].国防科技大学学报,2004,26(2):30-34.LI Zonghua,GUO Fucheng,ZHOU Yiyu,et al.The observability conditions of the single observer passive location and tracking based on TOA and DOA measurements[J].National University of Defense Technology,2004,26(2):30-34.
[5]杨莘元,郑思海.基于运动辐射体TOA和DOA测量的单站被动定位算法[J].电子学报,1996,24(12):66-69.YANG Xinyuan,ZHENG Sihai.A single observer passive location method based on TOA and DOA measurements[J].Acta Electronica Sinica,1996,24(12):66-69.
[6]王杰贵,罗景青,尹成友,等.固定单站对机动目标无源定位I MM 算法[J].信号处理,2002,18(2):137-140.WANG Jiegui,LUO Jingqing,YIN Chengyou,et al.The Interacting multiple-model algorith m for passive localization of maneuvering target by single fixed station[J].Signal Processing,2002,18(2):137-140.
[7]孙仲康,郭福成,冯道旺.单站无源定位跟踪技术[M].北京:国防工业出版社,2008.
[8]LI Zonghua,FENG Dao wang,SUN Zhongkang,ZHOU Yiyu.Passive location using time of arrival along with direction of arrival and its changing rate[C]//2003 IEEE Inter national Conference on Robotics,Intelligent Systemsand Signal Processing.Changsha,China:IEEE,2003:261-265.
