基于减量学习的鲁棒稀疏最小二乘支持向量回归机
2011-08-21高润鹏
高润鹏,伞 冶,朱 奕
(哈尔滨工业大学控制与仿真中心,黑龙江 哈尔滨 150001)
0 引言
支持向量机[1](support vector machine,SVM)是Vapnik提出的一种基于统计学习理论的学习机器,与神经网络相比,它可以解决小样本、“维数灾”和局部极值解等问题,具有较强的泛化能力,并在目标声识别[2]、爆破震动预测[3]等实际问题中得到广泛应用。它采用自上而下的学习方式,选取损失函数如ε不敏感损失函数、Laplacian损失函数、Huber损失函数或分段损失函数,得到具有一定鲁棒性和稀疏性的模型。
最小二乘支持向量机[4](least squares SV M,LSSV M)是SV M的扩展算法,求解算法为解线性方程组,训练速度明显加快。LSSV M的求解算法主要有共轭梯度法[4]、降阶法[5]和序列最小优化算法[6]等。但LSSV M采用误差的平方和作为损失函数,当数据混有非高斯分布长尾噪声时,算法鲁棒性变差。为此Suykens[7]提出加权LSSV M (weighted LSSV M,WLSSV M),它根据误差信息赋予样本权重,对异常样本赋予极小的权重值以抑制它的影响。但当异常样本较多时,WLSSV M检测和抑制异常样本能力下降。采用迭代 WLSSV M[4]及改进算法[8-9]可增强算法的鲁棒性,但需要多次训练 WLSSV M且训练时间较长。De Brabanter[10]实验对比四种权值函数的迭代WLSSV M算法的鲁棒性。张淑宁[11]采用鲁棒学习提高LSSV M的鲁棒性。温雯[12]采用假设检验方法检测异常样本,剔除它并使用减量学习更新模型,算法的鲁棒性增强。采用以上算法LSSV M鲁棒性在一定程度上得到增强,但LSSV M采用等式约束,导致算法缺乏稀疏性,过多的支持向量使得模型结构复杂、预测时间长。因此有学者提出改进算法提高稀疏性,如先学习训练样本得到初始模型。1)按剪枝策略选择部分支持向量,直接删除它并重新训练LSSV M,重复该过程直到事先定义的性能指标下降为止。剪枝策略主要有:最小支持向量谱[13],模型引入误差最小[14]及其改进算法[15]等。缺点是需要重复训练LSSV M,计算量较大。2)在高维特征空间采用向量相关分析约简支持向量[16-17],约简模型性能不变,缺点是支持向量约简率较低。学者提出改进算法[18-20]以提高支持向量约简率。Yang[21]提出自适应剪枝算法得到模型稀疏解。Zhao[22]将使目标函数值下降较多的样本加入支持向量集。采用以上算法可提高LSSV M稀疏性,但当数据混有异常样本时,它却将异常样本当作支持向量,算法鲁棒性差。为克服前人单一提高鲁棒性或稀疏性的缺点,本文提出鲁棒稀疏最小二乘支持向量回归机(least squares support vector regression machine,LSSVRM)算法。它从初始LSSVRM模型出发,自下而上的采用循环逐一删除异常样本或不重要样本。为增强算法鲁棒性,采用基于留一误差的鲁棒“3σ”准则检测并删除异常样本。为提高算法稀疏性,采用基于最小绝对留一误差的剪枝策略删除不重要样本。为降低算法计算量,采用快速留一误差和减量学习更新模型。
1 最小二乘支持向量回归机
设训练数据集 { (xi,yi),输入xi∈Rz,输出yi∈R,根据结构风险最小化原则,Suykens[4]将损失函数由误差和转变为误差的平方和,约束条件由不等式约束转变为等式约束,LSSVRM可以表示为如式(1)所示优化问题:

式(1)中,φ(·)是将输入空间映射到高维特征空间的非线性函数;w表示模型的复杂度;e=[e1,…,en]T表示经验误差;γ∈R+是正则化参数。为解这个约束优化问题,利用对偶优化和Lagrange函数把约束优化问题转化为无约束优化问题:

式(2)中,α= [α1,…,αn]T为Lagrange乘子。由最优化条件可得:

式(3)中,y = [y1,…,yn]T;α = [α1,…,αn]T;1=[1,…,1]T;I是 单 位 矩 阵;Κij= φ (xi)Tφ(xj)=k(xi,xj);k(xi,xj)是核函数,常用的核函数有高斯核函数k(xi,xj)=exp(-‖xi-xj‖2/ρ2)和多项式核函数k(xi,xj)=/μ+1)d。
求解式(3)线性方程组可以得到α和b。回归函数f(x)如式(4)所示:

2 鲁棒稀疏LSSVRM算法
由于设备故障、电磁干扰和过失误差等因素影响,实际数据不可避免地混入异常值,所以研究LSSVRM的鲁棒稀疏算法具有较大的实用价值。因此本文提出鲁棒稀疏LSSVRM算法,它采用自下而上的学习方式,首先学习训练样本得到初始LSSVRM模型,获得每个样本的误差信息作为先验知识。采用循环逐一删除异常样本方式,即每次循环只考察异常性最大的样本,判断它是否是异常样本,是则删除该异常样本,学习剩余样本更新模型,使回归曲面能逐步得到纠正,提高下一次循环异常样本的检测率,以增强算法鲁棒性。当异常样本删除完毕,再逐一删除模型中不重要样本,并学习剩余样本更新模型,直到模型泛化性能略有下降为止,以提高算法的稀疏性。
要实现上述算法主要解决以下三个问题:一是采用什么方法检测异常样本,二是如何选择不重要样本,三是如何快速更新模型,以降低计算量。因此本文采用基于快速留一误差的鲁棒 “3σ”准则检测异常样本,选择具有最小绝对留一误差的样本作为不重要样本,采用减量学习快速更新模型。
2.1 快速留一误差
留一误差Δyi是用除第i个样本外的其余样本拟合回归曲面,计算第i个样本的预测值,则Δyi=yi-。由于LSSVRM采用误差的平方和作为损失函数,异常样本将回归曲面拉向自身,使异常样本的误差减小,正常样本的误差增大,而计算样本的留一误差过程中回归曲面没有该样本,所以留一误差较普通误差更能如实反映样本的异常性。因此本文采用留一误差代替普通误差。但计算训练样本的留一误差相当于训练n次n-1个样本的LSSVRM模型,其中n为模型中样本个数。计算复杂度为O(n4),计算量非常大,不适合训练样本较多的情况。但采用快速留一误差[23],在得到LSSVRM模型的基础上,只进行简单运算即可得到所有训练样本的留一误差,计算复杂度降为O(n),降低了计算量。第i个样本的留一误差Δyi如式(5)所示。
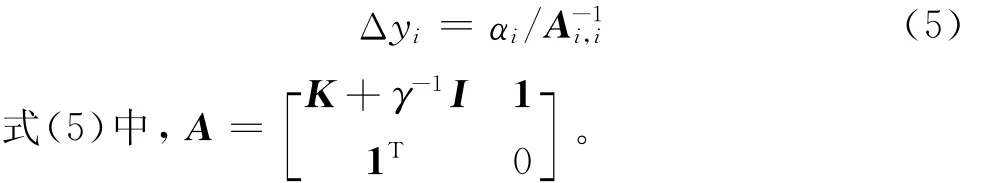
下面以计算第一个样本的留一误差为例,简要推导快速留一误差的计算公式,由式(3)可知,

式(6)中,c1= [k(x2,x1),…,k(xn,x1),1]T;c11=k(x1,x1)+γ-1;C1由矩阵A去掉第一行和第一列得到。
删除第一个样本(x1,y1),学习剩余样本得到模型参数α(-1),b(-1),如式(7)所示。


由式(3)和式(6)可得从第2到n+1个等式方程。

由式(3)线性方程的第一个等式方程得:

结合式(10)和式(11)得:

由方块矩阵求逆引理可得:


因为样本顺序可以任意调换,所以推广到所有训练样本,第i个样本的留一误差Δyi为:

由于A-1已知,由式(15)可知,通过简单计算即可快速得到所有训练样本的留一误差。
2.2 基于留一误差的鲁棒“3σ”准则检测异常样本
由于训练数据含有异常样本,样本的留一误差分布具有长尾性,不符合N(0,σ2)标准高斯分布,基于均值和方差的普通“3σ”准则对异常误差敏感,鲁棒性差,所以采用它检测异常样本的能力急剧下降。因此本文采用鲁棒“3σ”准则[24],按式(16)计算第i个样本的标准留一误差:

因此,异常样本的判断准则为样本的标准留一误差SLOOi是否大于阈值c,大于c则为异常样本,否则为正常样本。

异常样本检测停止条件:样本最大标准留一误差不大于阈值c,即max(SLOOi)≤c。c值越大,检测到异常样本的数目相对越少,将异常样本当作正常样本的机率越大。反之,c值越小,检测到异常样本的数目相对越多,将正常样本当作异常样本的机率越大。对于异常样本不太多的情况,取c=3较合适,因为对于符合标准高斯分布误差,SLOOi>3的概率是0.26%。对于异常样本较多的情况,取c=2.5较合适。
2.3 基于最小绝对留一误差的剪枝策略
由于LSSVRM模型缺乏稀疏性,为得到稀疏模型,采用剪枝策略删除不重要样本使得模型结构简单、预测时间短,但同时模型会损失部分信息,从而导致模型泛化性能下降。样本剪枝策略主要有Suykens[13]提出的删除较小的样本,因为ei=αi/γ,相当于构造误差不敏感域,但删除该样本后模型引入误差不保证最小,因此按此剪枝策略得到的稀疏模型泛化性能不理想。De Kr uif[14]提出删除模型引入误差最小的样本,如式(18)所示。但当γ=∞时,相当于目标函数没有正则化项,矩阵B经常奇异,而且计算矩阵B的逆矩阵计算量较大;当γ<∞时,需要进行复杂矩阵运算。

式(18)中,di=[0,…,0,1,0,…,0]T,di中第i个元素为1K是核矩阵;Y = [y1,…,yn,0]T。Kuh[15]提出删除具有最小的样本,它是删除样本后模型引入误差的另一种计算公式。本文采用删除具有最小绝对留一误差的样本,因为由可知,删除arg min()样本对模型的引入误差最小,所以模型信息损失相对较小,模型泛化性能也相对要好。
剪枝停止条件是样本最小绝对留一误差大于阈值ζ,即min()>ζ。阈值ζ决定被删除不重要样本的个数,ζ值越大,则被删除不重要样本个数越多,模型泛化性能越差。反之,ζ值越小,则被删除不重要样本个数越少,模型泛化性能相对越好。阈值ζ的取值与具体数据集样本的输出有关,要在模型稀疏性和泛化性能取折衷,由实际应用需求决定。
2.4 减量学习
假设当前LSSVRM模型由N个样本建立,删除一个样本后,需要训练剩余N-1个样本以得到新模型,训练算法计算复杂度为O((N-1)3),计算量较大。为减少计算量,降低计算复杂度,采用减量学习更新模型,计算复杂度降为O((N-1)2)。
设当前模型由N个样本建立,即ANaN=YN,且

从模型中删除样本 (xk,yk),则新模型参数为

为避免矩阵AN-1求逆,A由式(20)得到[25]

则N-1个样本对应的LSSVRM模型参数aN-1= [αb]T,可由式(19)得到。
2.5 算法复杂度分析
设当前LSSVRM模型由N个样本建立,不论是采用2.2节基于留一误差鲁棒“3σ”准则检测异常样本或2.3节基于绝对最小留一误差的剪枝策略,均采用2.1节快速留一误差公式(5)计算所有样本的留一误差,计算复杂度为Ο(N)。然后通过减量学习删除一个样本后得到由(N-1)个样本建立的模型,则执行一次减量学习的计算复杂度为Ο((N-1)2)。鲁棒稀疏LSSVRM算法删除所有异常样本和不重要样本的总计算复杂度为:

式(21)中,Noutlier是异常样本的个数,m是被删除不重要样本的个数。但异常样本和被删除不重要样本的总数小于训练样本,总计算复杂度小于直接训练一次LSSVRM复杂度Ο(n3)。加上2.2节异常样本检测阶段计算标准留一误差过程中的中位数等计算,则鲁棒稀疏LSSVRM算法总计算量与加权LSSVRM相当,即相当于训练两次LSSVRM,所以算法训练时间和加权LSSVRM训练时间接近。
2.6 完整算法流程
鲁棒稀疏LSSVRM算法步骤如下:
Step1:学习训练样本得到初始LSSVRM模型。
Step2:按式(5)和式(16)计算训练样本标准留一误差,判断样本最大标准留一误差是否大于阈值c,是则删除该异常样本,并采用减量学习更新模型,返回Step2;否则异常样本检测和删除阶段停止,转向Step3。
Step3:按式(5)计算训练样本的留一误差,判断样本最小绝对留一误差是否小于或等于阈值ζ,是则删除该样本,并采用减量学习更新模型,返回Step3;否则输出鲁棒稀疏LSSVRM模型。
鲁棒稀疏LSSVRM算法流程图如图1所示。

图1 鲁棒稀疏LSSVRM算法流程图Fig.1 The flowchart of r obust sparse LSSVRM algorith m
3 数值仿真
本文实验在2.7 GHz奔腾双核处理器,2 GB内存的台式机进行,程序由Matlab7.10实现。选用高斯核函数,LSSVRM模型参数为正则化参数γ和高斯核参数ρ2,最优参数由留一交叉验证法[23]确定。噪声环境下回归模型的性能评价指标:
1)测试绝对平均误差,如式(22)所示:

式(22)中,Ntest是测试样本的个数。
2)统计学家[25]提出如式(23)所示指标:

合理模型R2的取值范围是0≤R2≤1。R2=1表示最佳拟合,当R2<0时,说明模型已到达“崩溃点”。
算法说明:本文算法鲁棒稀疏LSSVRM(r obust sparse LSSVRM,RSLSSVRM),对比算法有LSSVRM、加权LSSVRM (weighted LSSVRM、WLSSVRM),鲁棒 LSSVRM (r obust LSSVRM,RLSSVRM),它是本文算法只进行异常样本检测和删除阶段得到的鲁棒LSSVRM模型,用于考察本文算法的鲁棒性。
3.1 仿真数据集
仿真数据集中训练样本由采样函数sinc(x)和噪声函数Fε(e)叠加产生,sinc(x)在[-10,10]内等间隔采样产生,个数为200。采用式(24)生成噪声:

式(24)中,F0(e)是符合 N(0,0.09)的高斯噪声;H(e)是异常噪声;ε是异常样本占训练样本的比例,0≤ε≤1。H(e)为产生异常样本的噪声,本文采用符合[-1,3]均匀分布噪声。为全面考察算法的性能,异常样本占训练样本的比例ε从5%开始以5%的增幅增加至45%,异常样本在定义域内随机产生,生成9个训练集。测试样本由采样函数sinc(x)在[-10,10]等间隔采样产生,不含噪声,个数为200。参数设置为:γ=10,ρ2=1,阈值c=3,阈值ζ=0.05。四种算法在9个训练集上的实验结果如表1所示,对比指标有:MAE、R2和训练时间(training ti me,TT)。
首先考察算法的鲁棒性,各算法初次到达“崩溃点”时R2数据已加下划线,由表1可以看出,当异常样本占训练样本比例较低时,如ε为5%、10% 时,RLSSVRM和WLSSVRM的鲁棒性能都很好,但RLSSVRM的性能优于 WLSSVRM。当ε增加至15%和20%时,WLSSVRM性能下降,但还没有到达“崩溃点”,而RLSSVRM鲁棒性能依然很强。对于LSSVRM,当ε=10%时,R2已为负数,说明模型预测结果不合理,由此可见LSSVRM对异常样本非常敏感。当异常样本比例为25% 时,WLSSVRM的R2=-0.781 5,算法已到达“崩溃点”,此时 MAE=0.156 7,预测结果已不合理。而RLSSVRM鲁棒性一直很好,直到异常样本比例达到45% 时,R2=-0.065 5,已到达算法的“崩溃点”,MAE =0.121 2。这是因为异常样本比例已接近50%,初始LSSVRM模型几乎无法提供有价值信息,正常样本和异常样本的留一误差相差不大,所以基于中位数和鲁棒标准差的“3σ”准则也很难辨别正常样本和异常样本。
从算法训练时间看,9个训练集上,RSLSSVRM和WLSSVRM训练时间接近,实验结果与2.4节算法复杂度分析结果吻合。
再考察算法的稀疏性,由表1实验结果可以看出,异常样本比例ε是5%、20%、30%、35%和40%时,RSLSSVRM在得到RLSSVRM基础上,通过不断删除绝对留一误差最小的样本使模型稀疏,因此损失部分模型信息,所以RSLSSVRM模型的MAE和R2比RLSSVRM模型性能略差。而异常样本比例ε是10%、15%和25%时,RSLSSVRM模型的MAE和R2优于RLSSVRM模型,这是因为稀疏模型结构简单,泛化性能可能更好,有时对误差较小样本的过分拟合,可降低模型的泛化性能。
为分析阈值c对RSLSSVRM算法鲁棒性的影响,固定阈值ζ=0.05,c值分别取2.5、3和3.5,在9个训练集进行实验,对比指标为:异常样本个数(nu mber of outliers,NO)、MAE和R2,实验结果如表2所示。由表2可以看出,RSLSSVRM算法在c=[2.5,3.5]取得了较好的鲁棒性。随着c值的减小,检测的异常样本数目增多,如c=2.5时,当异常样本数目较少时,由于很多正常样本被当作异常样本被删除,导致模型MAE和R2相对较差。随着c值的增大,检测的异常样本数目减少,如c=3.5时,当异常样本较多时,由于很多异常样本被当作正常样本而被保留,也导致模型MAE和R2相对较差。所以对于异常样本不太多时取c=3较合适;异常样本较多时,取c=2.5;实验结果也验证了2.2节理论分析。
为分析阈值ζ对RSLSSVRM算法稀疏性的影响,固定阈值c=3,ζ值分别取0.02、0.05和0.08,在9个训练集进行实验,对比指标:被删除不重要样本个数(number of eli minated uni mportant samples,NEUS)、MAE和R2,实验结果如表3所示。由表3可以看出,随着ζ值增大,被删除的不重要样本明显增多,RSLSSVRM模型信息损失越多,模型MAE和R2性能越差。随着ζ值减小,被删除的不重要样本越少,RSLSSVRM模型信息损失越少,模型的MAE和R2性能相对要好。考虑到模型的稀疏性和泛化性能的折衷,实际应用中根据需求确定阈值ζ,对于仿真数据集取ζ=0.05较合适,实验结果也验证了2.3节理论分析。

表1 4种算法在仿真数据集上的测试结果Tab.1 Testing results of four algorith ms on si mulation datasets

表2 阈值c对RSLSSVRM算法鲁棒性的影响Tab.2 Threshold c effects on the robustness of RSLSSVRM algorith m

表3 阈值ζ对RSLSSVRM算法稀疏性的影响Tab.3 Thresholdζeffects on the sparseness of RSLSSVRM algorith m
3.2 标准数据集
为进一步测试算法的有效性,采用5个标准数据集[26]:Triazines、Bodyfat、Mpg、Housing和 Mg,输入数据归一化为[0 1],输出数据不变,数据集描述和参数设置如表4所示。4种算法在5个标准数据集上实验结果如表5所示。对比指标有:异常样本个数NO、被删除不重要样本个数NEUS、R2和训练时间TT。由表5可以看出,与WLSSVRM相比,在鲁棒性方面RLSSVRM均取得较好的拟合性能。在稀疏性方面,在数据集Bodyfat、Mpg和Mg,RSLSSVRM在大幅减少支持向量的同时,拟合性能略差于RLSSVRM,但在数据集Triazines和Housing,RSLSSVRM拟合性能优于RLSSVRM。总体上,标准数据集实验结果表明RSLSSVRM性能优于WLSSVRM和LSSVRM。在训练时间方面,RSLSSVRM所需时间与WLSSVRM相当。

表4 数据集描述与参数设置Tab.4 Dataset descriptions and parameter setting
4 结论
为解决LSSVRM在噪声环境下鲁棒性不强和缺乏稀疏性问题,在得到初始LSSVRM模型基础上,提出采用自下而上的学习方式和基于减量学习逐一删除异常样本或不重要样本的鲁棒稀疏LSSVRM算法。并采用基于快速留一误差的鲁棒“3σ”准则检测异常样本和基于最小绝对留一误差的剪枝策略删除不重要样本。理论分析和数据集实验结果表明:采用基于留一误差的鲁棒“3σ”准则检测并删除异常样本后,新算法鲁棒性明显增强;采用基于最小绝对留一误差的剪枝策略删除不重要样本后,在模型泛化性能略有下降的情况下,支持向量数目大幅减少,新算法稀疏性明显提高;采用快速留一误差和减量学习更新模型后,降低了计算量,新算法训练时间与WLSSVRM训练时间相当。
[1]Vapnik V N.The nature of statistical lear ning theory[M].New Yor k:Springer-Verlag,1995.
[2]李京华,张聪颖,倪宁.基于参数优化的支持向量机战场多目标声识别[J].探测与控制学报,2010,32(1):1-5.LI Jinghua,ZHANG Chongying,NI Ning.Multi-target acoustic identification in battlefield based on SV M of parameter opti mization[J].Jour nal of Detection &Control,2010,32(1):1-5.
[3]丁凯,方向,陆凡东,等.基于支持向量机的振动加速度峰值预测模型[J].探测与控制学报,2010,32(4):38-41.DING Kai,FANG Xiang,LU Fandong,et al.Forecasting model of blasting vibration acceleration peak-value based on SV M[J].Jour nal of Detection & Contr ol,2010,32(4):38-41.
[4]Suykens J A K,Van Gestel T,De Brabanter J,et al.Least squares support vector machines[M].Singapore:World Scientific,2002.
[5]Chu W,Ong C J,Keerthi S S.An i mproved conjugate gradient scheme to t he solution of least squares SV M[J].IEEE Trans on Neural Net works,2005,16(2):498-501.
[6]Keerthi S S,Shevade S K.SMO algorith m for leastsquares SV M for mulations[J].Neural Co mputation,2003,15(2):487-507.
[7]Suykens J A K,De Brabanter J,Lukas L,et al.Weighted least squares support vector machines:robustness and sparse approxi mation[J].Neurocomputing,2002,48:85-105.
[8]吕剑峰,戴连奎.加权最小二乘支持向量机改进算法及其在光谱定量分析中的应用[J].分析化学,2007,35(3):340-344.LU Jianfeng,DAI Liankui.Improved weighted least squares support vector machines algorith m and its applications in spectroscopic quantitative analysis[J].Chinese Jour nal of Analytical Chemistr y,2007,35(3):340-344.
[9]包鑫,戴连奎.加权最小二乘支持向量机稳健化迭代算法及其在光谱分析中的应用[J].化学学报,2009,67(10):1 081-1 086.BAO Xin,DAI Liankui.Robust iterative algorit h m of weighted least squares support vector machine and its application in spectral analysis[J].Acta Chi mica Sinica,2009,67(10):1 081-1 086.
[10]De Brabanter K,Pelck mans K,De Brabanter J,et al.Robustness of ker nel based regression:a co mparison of iterative weighting schemes[C]//Berlin,Ger many:Springer-Verlag,2009.
[11]张淑宁,王福利,尤富强,等.基于鲁棒学习的最小二乘支持向量机及其应用[J].控制与决策,2010,25(8):1 169-1 172.ZHANG Shuning,WANG Fuli,YOU Fuqiang,et al.Robust least squares support vector machine based on robust learning algorith m and its application[J].Control and Decision,2010,25(8):1 169-1 172.
[12]温雯,郝志峰,杨晓伟,等.基于假设检验及异常点剔除的稳健LS-SV M 回归[J].模式识别与人工智能,2010,23(2):241-249.WEN Wen,HAO Zhifeng,YANG Xiaowei,et al.Robust least squares support vector machine regression based on hypothesis testing and outlier-eli mination[J].Patter n Recognition and Artificial Intelligence,2010,23(2):241-249.
[13]Suykens J A K,Lukas L,Vandewalle J.Sparse approximation using least squares support vector machines[C]//Geneva,Switzerland:IEEE Press,Florida,2000.
[14]De Kr uif B J,De Vries T J A.Pr uning err or mini mization in least squares support vector machines[J].IEEE Trans on Neural Net wor ks,2003,14(3):696-702.
[15]Kuh A,De Wilde P.Comments on"Pruning error minimization in least squares support vector machines"[J].IEEE Trans on Neural Net wor ks,2007,18(2):606-609.
[16]甘良志,孙宗海,孙优贤.稀疏最小二乘支持向量机[J].浙江大学学报(工学版),2007,41(2):245-248.GAN Liangzhi,SUN Zonghai,SUN Youxian.Sparse least squares support vector machine[J].Jour nal of Zhejiang University (Engineering Science),2007,41(2):245-248.
[17]Liang X,Chen R C,Guo X Y.Pruning support vector machines without altering perfor mances[J].IEEE Trans on Neural Net works,2008,19(10):1 792-1 803.
[18]陈爱军,宋执环,李平.基于矢量基学习的最小二乘支持向量机建模[J].控制理论与应用,2007,24(1):1-5.CHEN Aijun,SONG Zhihuan,LI Ping.Modeling method of least squares support vector regression based on vector base learning[J].Control Theory & Applications,2007,24(1):1-5.
[19]Liang X.An effective method of pr uning support vector machine classifiers[J].IEEE Trans on Neural Net works,2010,21(1):26-38.
[20]Li Q,Jiao L C,Hao Y J.Adaptive si mplification of solution for support vector machine[J].Patter n Recognition,2007,40(3):972-980.
[21]Yang X W,Lu J,Zhang G Q.Adaptive pr uning algorit h m f or least squares support vector machine classifier[J].Soft Co mputing,2010,14(7):667-680.
[22]Zhao Y P,Sun J G.Recursive reduced least squares support vector regression[J].Patter n Recognition,2009,42(5):837-842.
[23]Cawley G C,Talbot N L C.Preventing over-fitting during model selection via bayesian regularisation of the hyper-parameters[J].Jour nal of Machine Lear ning Research,2007,8(4):841-861.
[24]Maronna R A,Martin R D,Yohai V J.Robust statistics:t heor y and methods[M].England:John Wiley &Sons,2006.
[25]Cau wenberghs G,Poggio T.Incremental and decremental support vector machine learning[C]//Cambridge,MA:MIT Press,2001.
[26]Chang C C,Lin C J.LIBSV M:a library f or support vector machines[EB/OL].[2011-06-15]htt p://www.csie.ntu.edu.t w/~cjlin/libsv mtools/datasets/regression.
