电力系统PMU最优配置新方法

王家林，夏 立，吴正国，杨宣访

（海军工程大学电气与信息工程学院，武汉 430033）

随着电力系统规模的日益扩大，对如何及时获取电网信息并对电力系统进行实时监控和管理提出了更高更复杂的要求。同步相量测量［1～3］是应复杂电力系统实时动态监控的需要而兴起的一项技术 －－ 同 步 相 量 测 量 装 置PMU（phasor measurement unit），可以在安装地点对电力系统相应的各种参数进行同步的采集和实时的计算，并根据不同的电力系统监控模式，将检测数据传送给监控网络中数据需求节点。潮流计算［4］用以分析电力系统在某一时间断面系统各状态变量值与系统内的功率分布情况，其计算结果为系统稳定性分析、保护与重构等提供初始条件和判别依据，对系统在线状态计算、系统状态预估等具有重要的意义。因此根据电力系统网络结构优化配置PMU，测出部分节点的电压相量，使得潮流方程组可以直接、快速、高精度求解是非常有意义的［5］。文献［6～8］采用优化算法求解PMU最优配置问题，但提出的判断PMU配置方案是否满足潮流方程直接可解的方法过于繁琐、在节点数较多的系统中难以表达且算法实现困难；文献［9］提出基于动态关联度的方法在求解速度上有一定优势，但易陷入局部最优解。本文根据电力系统导纳矩阵和节点关联矩阵的特点，指出电力系统潮流方程的特征可用系统关联矩阵来描述，在此基础上提出了一种基于关联矩阵的满足潮流方程直接可解的电力系统PMU最优配置方法，并以IEEE14节点系统说明了算法原理，最后利用IEEE30节点、新英格兰39节点、IEEE57节点、IEEE118节点系统对该算法进行验证，给出IEEE30节点、新英格兰39节点的分步配置算法实现的步骤和结果，并与已有方法得到的结果进行比较，结果表明该算法是有效的，具有简单、易于实现的优点，在满足潮流方程直接可解的基础上能有效减少PMU配置数目。

1 考虑潮流方程直接可解PMU配置方法

假设电力系统有n个节点，其中节点j为平衡节点，潮流问题可归结为由系统各节点给定的复功率求解各节点电压相量的问题，因此潮流方程是一组关于电压相量的非线性方程组［10］：

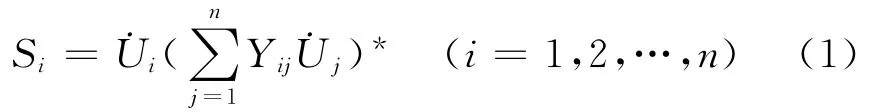
式中：Si＝Pi＋j Qi为节点i的注入功率；˙Ui＝Ui∠θi为节点i的电压相量；Yij为节点导纳矩阵Y中的元素。

电力系统的结构存在高度的稀疏性，若利用此特点适当配置PMU便能求解前i－1个方程，使得在求解第i个功率方程时式（1）右端最多只有一个未知节点电压相量 ，则有

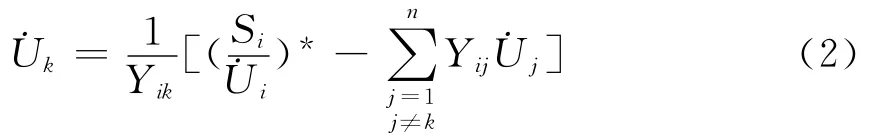
若从i＝1到i＝n－1的每步均能实现上述条件，则求解潮流方程可以不必迭代，此方法称为基于PMU的电力系统潮流直接解法。

2 基于关联矩阵的电力系统PMU配置方法

由于电力网络本身的结构特点，电力系统导纳矩阵和节点关联矩阵维数相同且矩阵元素非零元位置相同，以图1IEEE14节点系统为例如图1所示。节点1为平衡节点，其潮流方程如下。

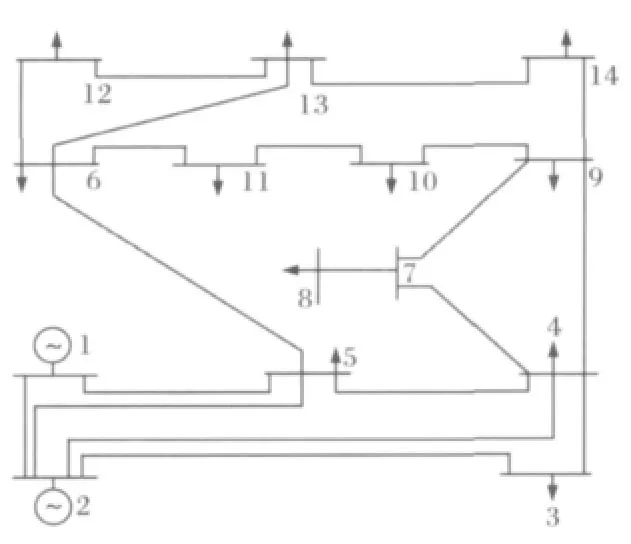
图1 IEEE14节点系统Fig.1 IEEE14－bus system

矩阵中每一行对应一个潮流方程，每一列代表对应的节点电压向量，“1”表示潮流方程中未知节点电压向量，以矩阵第5行为例，对应潮流方程（7），1、2、4、5、6列对应元素为“1”，则节点1、2、4、5、6电压向量未知。则潮流方程的特征可用关联矩阵来描述。

IEEE14节点电力系统的关联矩阵A如下。

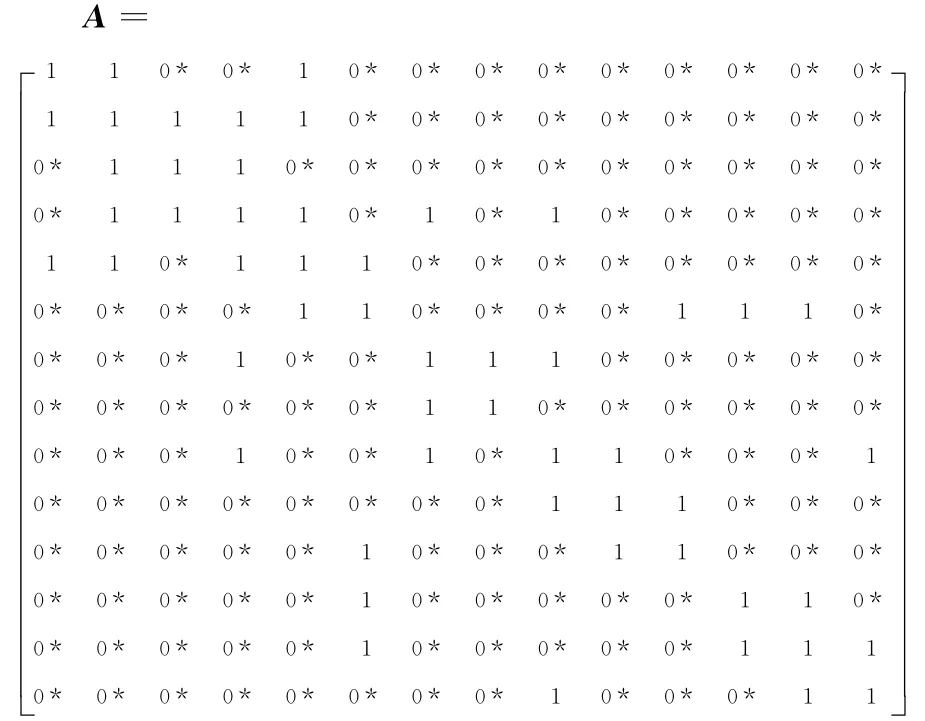
由关联矩阵与潮流方程的对应关系可以得出：

（1）若某一节点配置PMU，则潮流方程中该节点的电压向量已知，关联矩阵对应的列的元素全部置零。

（2）若矩阵中某一行只含一个“1”，则说明其对应的潮流方程只含有一个未知节点电压向量，方程可解，且该非零元所在列对应的节点的电压向量亦可知。（0＊表示潮流方程不含对应节点电压向量，0表示该节点配置PMU或节点电压向量已直接解出）以Ωi＝1表示在节点i配置PMU，Ωi＝0表示在节点i不配置PMU。

由于平衡节点必须配置PMU，则节点1的电压向量˙U1已知，关联矩阵对应的列的元素全部置零，得到关联矩阵B。

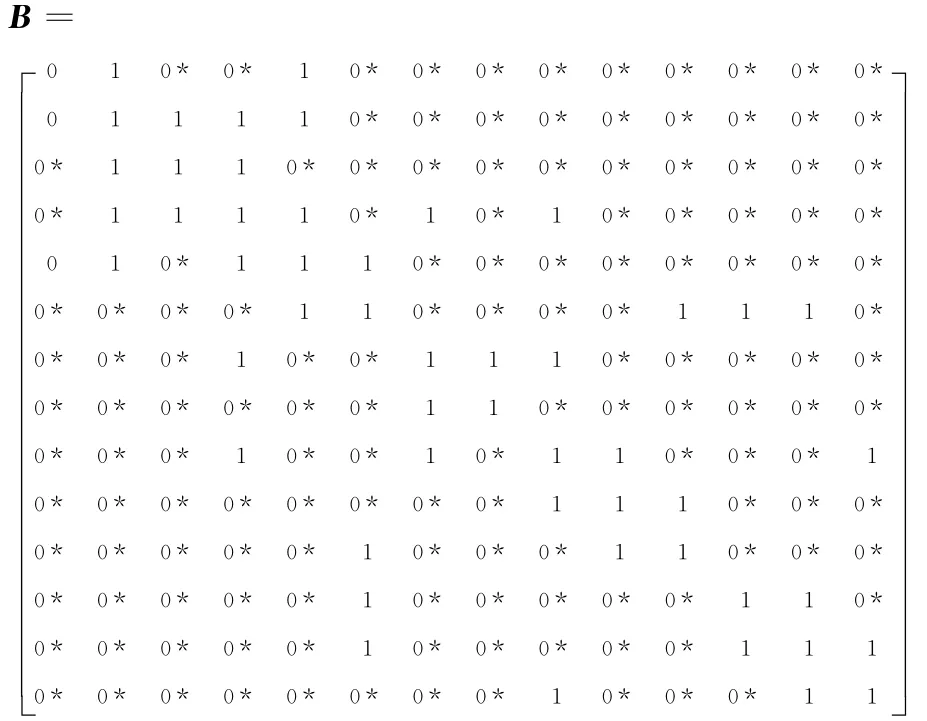
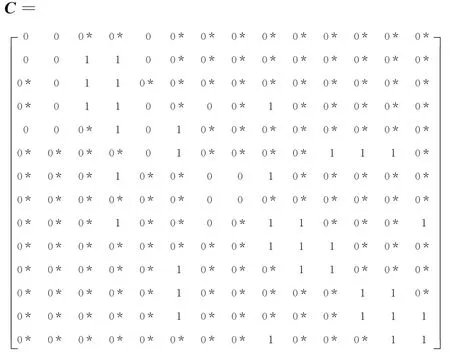
搜索关联矩阵B的每一行，计算每一行的“1”的个数，将含有最少相同“1”的个数的行编为一组，对应的将含有最少相同未知节点电压向量（一般为2个）的潮流方程编为一组，考虑配置最少PMU使这组方程直接可解。由矩阵B可以得出，第1行和第8行含有两个“1”，对应潮流方程（3）、（10）有两个未知节点电压向量。对于潮流方程（3），在节点2或5配置PMU可使方程直接可解，同理方程（10），则使这两个潮流方程直接可解的PMU最优配置方案为F1∶（Ω2∨Ω5）∧ （Ω7∨Ω8）＝1。方程解出，节点电压向量˙U2、˙U5、˙U7、˙U8已知，关联矩阵对应的列的元素全部置零得到矩阵C。

由矩阵C可以得出，第2、3、5、7行含有两个“1”，对应潮流方程（4）（5）（7）（9）有两个未知节点电压向量。使这四个潮流方程直接可解的PMU配置方案为（Ω3∨Ω4）∧ （Ω4∨Ω6）∧（Ω4∨Ω9）＝1，通过化简可以得到最优PMU配置方案为F2∶Ω4＝1。方程解出，节点电压向量˙U3、˙U4、˙U6、˙U9已知，关联矩阵对应的列的元素全部置零得到矩阵D。

由矩阵D可以得出，第9、10、11、12、14行含有两个"1" ，对应潮流方程（11）（12）（13）（14）（16）有两个未知节点电压向量。使这四个潮流方程直接可解的PMU配置方案为，（Ω10∨Ω14）∧（Ω10∨Ω11）∧ （Ω12∨Ω13）∧ （Ω13∨Ω14）＝1，通过化简可以得到最优PMU配置方案为F3∶Ω10∨Ω11∨Ω12∨Ω13∨Ω14＝1。方程解出，节点电压向量˙U10、˙U11、˙U12、˙U13、˙U14已知，关联矩阵对应的列的元素全部置零，得到全为零元的矩阵，至此，潮流方程完全解出。满足潮流方程直接可解的PMU配置方案为F∶F1∧F2∧F3＝1。结果如表1所示，与文献［8，9］结果相同。

由此得到一种基于关联矩阵的电力系统PMU分步最优配置方法：

1）根据电力系统拓扑结构和潮流方程组，形成得到电力系统关联矩阵，设定系统的平衡节点；

2）搜索关联矩阵的每一行，计算每一行的“1”的个数，将含有最少相同“1”的个数的行编为一组，对应的将含有最少相同未知节点电压向量（一般为2个）的潮流方程编为一组，得到使其直接可解的最优PMU配置方案Fi＝1，则其包含的节点电压向量均为已知；

3）将由2）得到的已知电压向量的节点在关联矩阵中对应的列置零，若部分置零后的矩阵中某一行只含一个非零元，则将该非零元所在列全部置零，重复步骤2）；

4）重复步骤2）和3），直至关联矩阵为零矩阵，得到满足潮流方程直接可解的PMU配置方案为F∶F1∧F2∧…Fk＝1。

表1 所提算法的PMU配置结果Tab.1 Results of optimal PMU placement

基于关联矩阵的电力系统PMU分步最优配置方法实现流程如图2所示。

图2 基于关联矩阵的PMU最优配置方法流程Fig.2 Flow chart of optimal PMU placement based on interactor matrix

几点说明：

（1）基于潮流可解的PMU最优配置的数学问题实质是：对于一个含n个未知数的方程组，寻找令最少的未知数为已知量而使方程可解。借鉴求解方程组（或系数矩阵的初等变换）得到最简等效方程组，再代入已知量求解未知数的方法，分步配置方案中每一步都是选取含有最少相同未知量个数的潮流方程编为一组，使其为最简方程组；对每一组潮流方程配置方案逻辑表达式进行简化，优选出最优配置方案，则每一组潮流方程直接可解的PMU配置方案是最优的。

（2）关于采用计算机求解“逻辑表达式”方法，分步配置方案为逻辑表达式，可利用计算机采用表格化简法（奎恩 －麦克路斯基法）进行基于逻辑代数的基本定律及规则的简化，形如（Ω7∨Ωj）∧（Ωj∨Ωk）＝1表达式可化简为（Ωj）∨ （Ωi∧Ωk）＝1（（Qq）∨（Qp）＝1），选取各项中含最少变量项为最优配置方案，得最优配置为Ωj＝1。

3 算例

按照图2所示的算法流程，本文以IEEE30、IEEE57、IEEE118节点系统、新英格兰39节点系统为例对文中提出的基于关联矩阵的PMU分步最优配置算法进行了测试，测试系统参数见表2，表3和表4为按照图2所示的算法以IEEE30节点系统、新英格兰39节点系统为例实现的步骤和结果。表5为本文所得到的最优配置结果与文献［5，7～9］所介绍方法的比较。

表2 测试系统参数Tab.2 Parameters of testing systems

表3、表4基于本文所提方法的实现步骤的和结果表明该方法的有效性，分步配置原理简单、易于实现。表5表明本文方法的优越性，特别是在较多节点情况下更能有效减少PMU配置数目。

表3 基于IEEE30节点系统的算法实现的步骤和结果Tab.3 Result and process of realization arithmetic on IEEE 30－bus system

表4 基于新英格兰39节点系统的算法实现的步骤和结果Tab.4 Result and process of realization arithmetic on New England 39－bus system

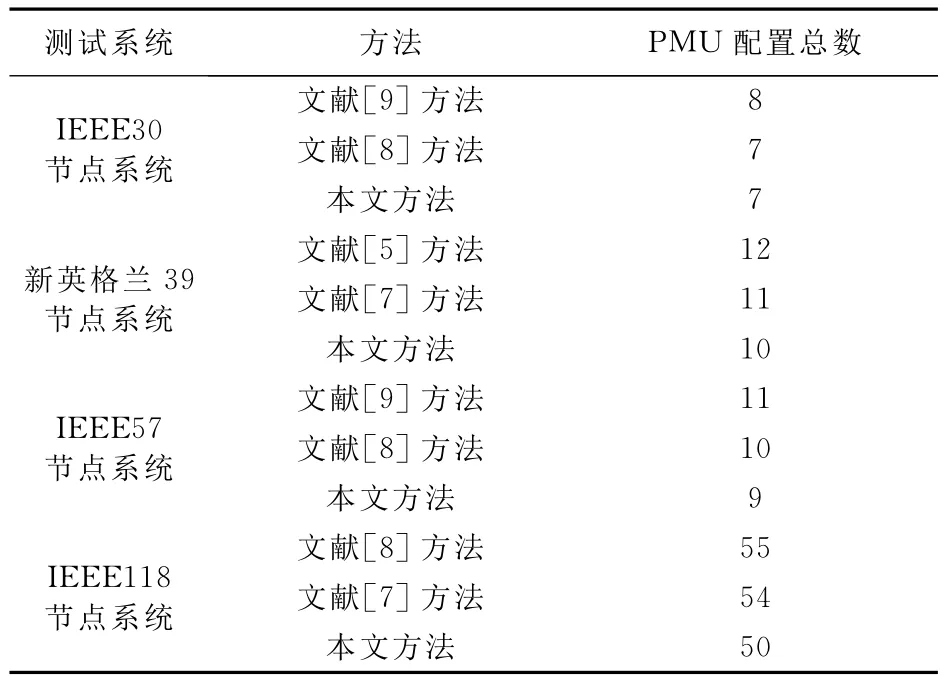
表5 不同算法的PMU配置结果比较Tab.5 Results of optimal PMU placement by different methods

4 结论

（1）根据电力系统导纳矩阵和节点关联矩阵，电力系统潮流方程特征可用系统关联矩阵来描述。

（2）基于关联矩阵的满足潮流方程直接可解的电力系统PMU分步最优配置方法，简单有效，易于实现，能减少PMU配置数目，可为电力系统配置PMU提供参考。

［1］Abbasy Nabil H，Ismail Hanafy Mahmoud.A unified approach for the optimal PMU location for power system state estimation［J］.IEEE Trans on Power Systems，2009，24（2）：806－813.

［2］Aminifar Farrokh，Lucas Caro，Khodaei Amin，et al.Optimal placement of phasor measurement units using immunity genetic algorithm［J］.IEEE Trans on Power Delivery，2009，24（3）：1014－1020.

［3］Gou Bei.Optimal placement of PMUs by integer linear programming［J］.IEEE Trans on Power Systems，2008，23（3）：1525－1526.

［4］张海波，张晓云（Zhang Haibo，Zhang Xiaoyun）.基于异步迭代的交直流互联系统分布式动态潮流计算（Distributed dynamic power flow for AC／DC interconnected power grid based on asynchronous iteration mode）［J］.电力系统自动化（Automation of Electric Power Systems），2009，33（18）：33－36.

［5］王克英，穆钢，韩学山，等（Wang Keying，Mu Gang，Han Xueshan，et al）.使潮流方程直接可解的PMU配置方案研究（Placement of phasor measurement unit for direct solution of power flow）［J］.中国电机工程学报（Proceedings of the CSEE），1999，19（10）：14－16，41.

［6］卫志农，常宝立，孙国强，等（Wei Zhinong，Chang Baoli，Sun Guoqiang，et al）.一种新的考虑电力系统潮流直接可解的PMU最优配置 （A new optimal configuration of synchronous phasor measurement unit considering direct solvable power flow）［J］.继电器（Relay），2005，33（21）：36－40.

［7］卫志农，孙国强，常宝立，等（Wei Zhinong，Sun Guoqiang，Chang Baoli，et al）.考虑电力系统潮流直接可解的同步相量量测单元最优配置（Optimal configuration of synchronous phasor measurement unit considering direct solvable power flow）［J］.电 网 技 术（Power System Technology），2005，29（1）：65－68.

［8］李新振，滕欢（Li Xinzhen，Teng Huan）.考虑潮流方程直接可解的PMU最优配置 （Optimal configuration of PMU considering direct solvable power flow）［J］.电力系统保护与控制（Power System Protection and Control），2009，37（16）：63－67.

［9］邢洁，韩学山，武鹏（Xing Jie，Han Xueshan，Wu Peng）.使潮流方程直接可解的PMU配置方法的改进（Improvement of optimal PMU placement for analytical solution of power flow node by node）［J］.电 网 技 术（Power System Technology），2006，30（11）：30－34.