多气象因素组合的输电线路风险分析
2011-08-16熊小伏王尉军沈智健程韧俐戴志勇
熊小伏,王尉军,于 洋,沈智健,程韧俐,戴志勇
(1.重庆大学输配电装备及系统安全与新技术国家重点实验室,重庆 400030;2.广东电网公司深圳供电局,深圳 518020)
输电线路大部分处于户外,恶劣天气条件下发生故障的可能性较大,研究输电线在不同气象条件下的风险分析方法,便于实现在线风险预警,提前做好安全措施。
已有较多文献研究了气象因素对电力系统可靠性的影响[1~3]。文献[4]将气候条件分为正常气候条件和不利气候条件,提出了分段模拟气候状态进行线路可靠性评估的方法。文献[5]采用Monte Carlo方法对气候区域和输电线路进行抽样,确定输电元件状态并进行电网可靠性计算。文献[6]提出了在恶劣天气条件下元件能否维修的分析方法。文献[7]建立了不同月份天气对输电线的影响及可靠性评估模型。
由上可见,在过去的研究中主要从电网的离线可靠性评估要求出发对考虑气象条件的输电线可靠性模型进行了较多研究,而对输电线在线风险分析和预警方法的研究较少。本文研究基于天气预报信息,建立计及气象等级的多因素输电线路风险分析方法,拟通过灰色模糊综合评判得到贴近实际的风险评判结果。
1 计及气象等级的不同气象因素输电线路故障率模型
对于不考虑气象条件的电网可靠性模型,一条输电线路只涉及一个故障率。但对于考虑处在不同气象条件下的输电线路应有不同的故障率。文献[8]给出了不同气象条件下的故障率公式,但公式仅用于计算不同气象因素下的输电线路故障率,并没有考虑在一种气象因素条件下,由于气象等级不同其故障率的差异性,如10级风与1级风之间的故障率差异较大。因此,更为合理的方法是建立单气象因素在不同气象等级下的故障率模型,可用下面的公式来求出:
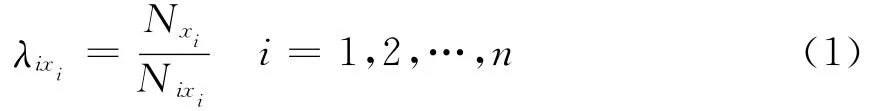
式中:λixi为第i种气象因素在气象等级xi下输电线路的故障率,是气象参数等级xi的函数;Nxi为第i种气象因素在气象等级xi下输电线路发生故障的次数;Nixi为第i种气象因素下出现气象等级xi的总次数,本文n=8。
依据某地区供电局提供的故障数据与气象部门的气候资料,结合式(1),得到各个气象因素在不同气象等级下的故障率,如表1所示。
从式(1)可知,针对每一种气象因素,输电线路故障率随着气象等级而变化的,如果线路处在单气象因素下,那么根据表1就可以确定线路所处的风险等级。而对于一条完整的输电线路,一般处于多种气象组合的综合气象中,即包含了不同的气象因素,也包含了不同的气象等级。因此,以表1的数据为基础,对处在多气象因素中的输电线路风险作出评判是非常有必要的,将有助于电力部分进行风险预警及制定维修策略。

表1 各个气象因素在不同气象等级下的故障率Tab.1 Failure rate under various meteorological factors of different meteorological grades
2 多气象因素的输电线路故障风险灰色模糊综合评判模型
2.1 建立综合评判模型的基本思路
在统计分析各个气象因素在不同气象等级下的故障率时,由于各个气象因素的信息充分度各不相同,使其具有很大程度的灰色性,如雷电数据可以直接测量获得,而覆冰只能通过其它气象信息推断获得。同样,依据天气预报得到的下一时段气象条件,由于气象条件的复杂多变性和多样性,使下一时段综合气象具有一定的模糊性。因此,采用灰色模糊综合评判可使评判结果更加客观可信[9,10]。其基本思路如下步骤:①建立与输电线路故障率有关的气象评判因素集;②根据下一时段的气象条件,获取各个气象因素的故障率;③通过经典的隶属度函数来表征因素集与评判集之间的模糊关系,通过建立灰色模糊评判矩阵来衡量各因素所能收集的信息量的不同;④利用改进的层次分析法确定权重集;⑤利用灰色模糊理论进行输电线路风险等级综合评判;⑥处理评判结果。
2.2 输电线路风险等级评判因素的确定
导致输电线路发生故障的气象因素很多,但根据电力部门多年的数据收集表明,引起线路故障的气象因素一般是雷电m1、覆冰m2、降雨m3、风m4、气温m5、台风m6、冰雹m7、雪m8。因此,本文就以这8种作为输电线路风险等级评判因素集,用故障率作为每种气象因素在某种气象等级下的评判取值,见表1所示。
2.3 表示评判结果等级的评判集的建立
评判集的等级划分视实际情况而定,等级太少会影响评判精度,太多则将增加运算的复杂度。本文将输电线路的风险等级划分为4个等级,即V={V1,V2,V3,V4},集合中各元素依次对应高风险、较高风险、一般风险和低风险。
2.4 灰色模糊评判矩阵的建立
2.4.1 模糊部分的确定
在模糊理论中,隶属度函数是用来表征因素集与评判集之间的模糊关系,其中,对于定量描述因素采用连续性赋值,对于定性描述因素则采用离散化赋值[11,12]。本文使用三角隶属函数来计算评判因素集中8个气象因素的隶属度,三角隶属度函数,表现形式简单,适宜工程计算,并且经验证发现,与其它的复杂形式隶属度函数得出的结果差别较小[13~15]。见图1,纵坐标μ(x)为x相对应的隶属度,横坐标x表示评判因素集中各气象因素故障率的实际取值。图中,x1<x2<x3<x4,x3~+∞,x4~x2,x3~x1,x2~0分别对应评判集中的V1~V4四个等级,而x4、x3、x2、x1分别表示V1~V4四个等级的阈值,取值根据统计数据和电力部门的具体情况而定,由线路运行情况和可靠性数据库得到(见算例)。
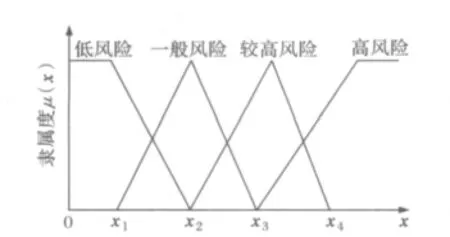
图1 三角隶属度函数Fig.1 Triangular subjection function
根据图1,各风险等级的相对于4个评判等级的隶属度为
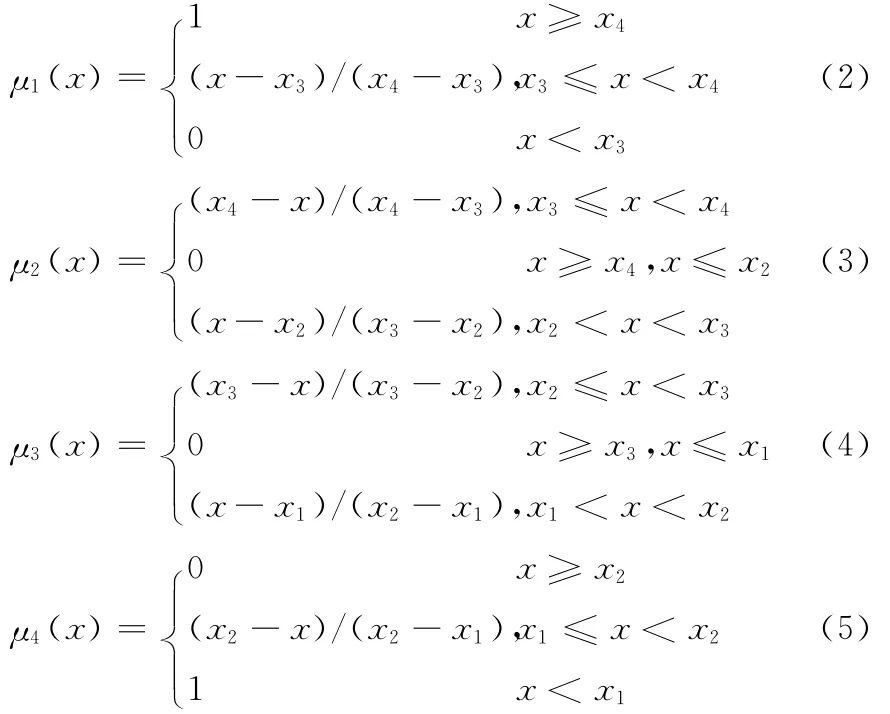
因此,根据图1及式(2)~(5),结合下一时段各气象因素故障率的实际取值,可确定灰色模糊评判矩阵中的模糊部分,而灰色部分由下节确定。
2.4.2 灰色部分的确定
在确定模糊部分时,各评判因素所能收集到的信息量不同,会造成所确定的模糊关系也存在不可信度。考虑到这种不可信度对风险等级判断的影响,在模糊关系矩阵中引入灰色部分,并使用一些描述性的语言来对应一定的灰度范围,将信息分成很充分、比较充分、一般、比较贫乏、很贫乏5类,分别对应灰度值0~0.2,0.2~0.4,0.4~0.6,0.6~0.8,0.8~1.0。
2.5 权重集的确定
由于各因素对线路故障的影响程度不尽相同,将各因素用权重的方式来定量反映在整体风险等级评判中所占的比重。本文采用改进的层次分析法[16]来处理各气象因素权重的确定方法,即把要解决的问题分为2层,目标层为输电线路风险等级,下一层为可能导致线路故障的8个气象因素,权重集的确定简化为确定8个气象因素的权重。

表2 1-9标度表Tab.2 1-9scale table
根据专家经验对m1~m8相对于风险等级的相对重要性两两比较,按表2所示1-9标度表示。
将两两比较的结果写成判断矩阵A。其中元素aij(i,j=1,2,…,n)表示评判因素mi与mj相比较的结果,且aii=1。当i≠j时,aij=1/aji,即标度具有互反性。
例如气象条件为低温,雷电黄色预警,大雨,5级大风,依据表2构造的判断矩阵为

确定判断矩阵后,推导得到拟优矩阵A*,利用方根法求得A*的特征向量,具体求解步骤参考文献[16]。取点灰度为0.3,可得权重集

式中8个元素分别对应气象因素m1~m8。以第1个元素为例,对应于“雷电”的权重为0.3445,其相对应的点灰度为0.3。
2.6 灰色模糊综合评判
输电线路的风险等级评判是对综合气象因素引起的风险变化趋势的分析,在模糊部分运算中采用(·,+)算子,而灰色部分运算中采用(⊙,+)算子,结合文献[12],合成的综合评判结果为
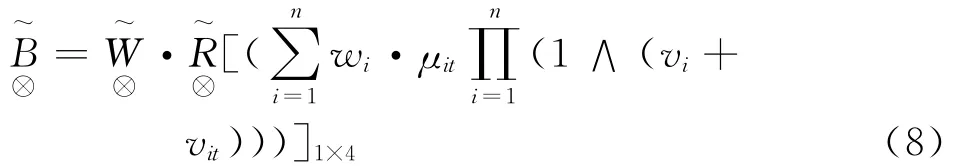
式中 表示权重集 表示与之对应的灰色模糊评判矩阵;wi、νi为各指标的权重及对应点灰度;μit、νit为各指标的隶属度及对应点灰度;t=1,2,3,4。
2.7 评判结果的处理
对评判结果的处理一般采用2种方法:①采用区间数的形式,转化为排序可能性矩阵,最后确定出可能性最大的评判因素,但是此方式计算较复杂;②直接利用隶属度最大原则和点灰度最小原则进行判断,但此方法在隶属度最大目点灰度也较大时很难下结论。针对这些不足,本文采用内积法和最大隶属度相结合的方法进行处理。
假设bi是的第i个向量,若令di=1-νi,其中νi表示灰度,则di表示bi的可信度。若令bi=(μi,di),综合评判是由bi的大小来确定,并可以简化为求解范数来比较大小,有

式中:[bi,bi]为向量bi的内积。至此可根据 ‖bi‖和最大隶属度原则得出综合评判结论。
3 算例分析
以某地区供电局管辖的220kV输电线路为例,应用本文提出的方法对其风险等级进行分析。
(1)根据下一时段的气象因素,假设为低温,雷电黄色预警,大雨,5级大风,下一时段不出现的气象因素为默认1级,结合表1,可得到如表3所示的该线路各气象因素故障率。
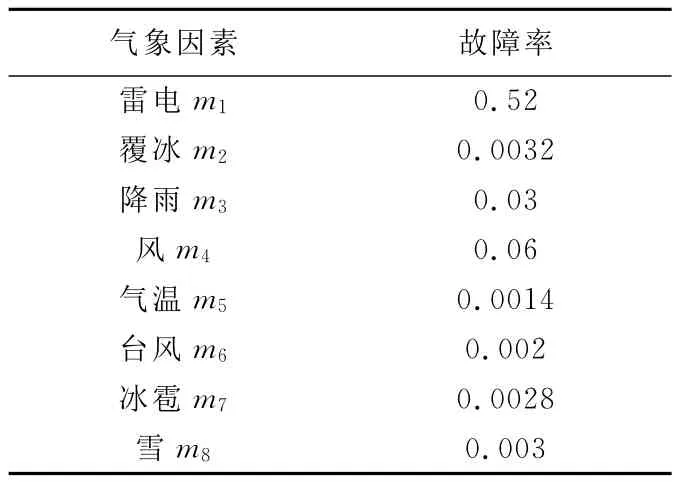
表3 各气象因素下的线路故障率Tab.3 Failure rate under various meteorological factors
(2)建立评判因素集。M={雷电m1、覆冰m2、降雨m3、风m4、气温m5、台风m6、冰雹m7、雪m8}。
(3)建立评判参考标准。针对风险等级的8个评判因素,根据输电线路运行、维修历史记录及相关数据库,并假设图1中x1~x4取值分别为8,6,4,2,得出风险等级评判因素的评判标准,见表4。
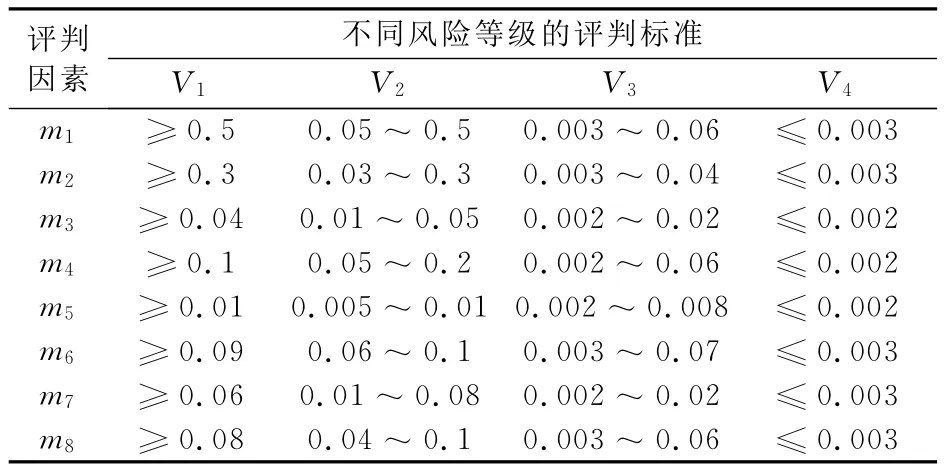
表4 风险等级评判因素的评判参考标准Tab.4 Reference standard for risk level evaluation factors
(4)建立各因素的灰色模糊评判矩阵。根据表4,将表3的各个气象因数故障率实际值代入式(2)~(5)可得各个气象因素对应各隶属度的值,并根据信息充分程度确定其灰度,得到一个8×4灰色模糊评判矩阵,见表5。
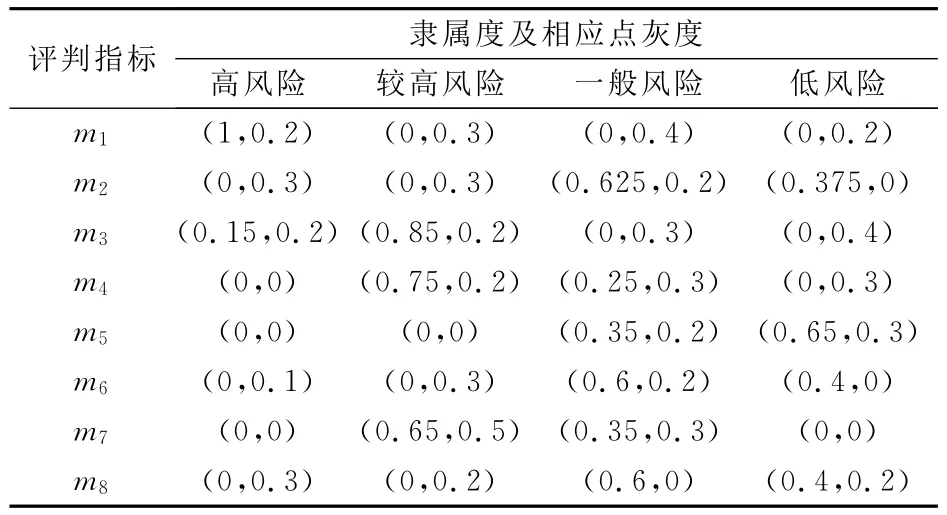
表5 风险等级评判的灰色模糊评判矩阵Tab.5 Grey fuzzy evaluation matrix for risk level evaluation
(5)进行灰色模糊综合评判,由式(8)可得

(6)处理评判结果。依据公式(9),对得到的综合评判向量取范数得 ‖b1‖ =1.0653,‖b2‖ =1.0607,‖b3‖ =1.0110,‖b4‖ =1.0005。根据最大隶属度原则可以判断该线路的风险级别为“高风险”。可以看出,若仅就隶属度来评判,该风险等级应属于“较高风险”,但由于该隶属度所对应的灰度较大,说明该隶属度并不可信,而基于灰色模糊综合评判的结论更加可信。
4 结语
输电线路风险预警是电网安全预警的主要内容之一,其难点在于如何建立预警方法和预警模型。本文首先建立了影响输电线路安全的主要气象因素的故障率模型,在此基础上应用灰色模糊理论构建了多气象因素组合的输电线路风险评判方法,由此可利用气象预报数据对未来时段输电线路风险作出综合评判,为制定安全预案和事故处理对策提供依据。
[1]Billinton R,Allan R N.Reliability Evaluation of Power System[M].New York:Pitman Press,1984.
[2]林智敏,林韩,温步瀛(Lin Zhimin,Lin Han,Wen Buying).天气条件相依失效模型的电力系统可靠性评估(Power system reliability evaluation based on weather dependent failure models)[J].华 东 电 力(East China Electric Power),2008,36(1):81-84.
[3]张腾,董洁,张波(Zhang Teng,Dong Jie,Zhang Bo).计及气候影响的配电线路可靠性分析(To evaluate the reliability of distribution system for weather factor)[J].山东大学学报(工学版)(Journal of Shandong University (Engineering Science)),2003,33(6):632-634,698.
[4]丁明,戴仁昶,洪梅,等(Ding Ming,Dai Renchang,Hong Mei,et al).影响输电网可靠性的气候条件模拟(Simulation to the weather condition affecting the reliability of transmission network)[J].电力系统自动化(Automation of Electric Power Systems),1997,21(1):18-20.
[5]刘洋,周家启(Liu Yang,Zhou Jiaqi).计及气候因素的大电力系统可靠性评估(Incorporating weather effect in bulk power system reliability evaluation)[J].电力自动化设备(Electric Power Automation E-quipment),2003,23(9):60-62.
[6]陈永进,任震,黄雯莹(Chen Yongjin,Ren Zhen,Huang Wenying).考虑天气变化的可靠性评估模型与分析(Model and analysis of power system reliability evaluation considering weather change)[J].电力系统自动化(Automation of Electric Power Systems),2004,28(21):17-21.
[7]王瑞祥,夏莹,熊小伏(Wang Ruixiang,Xia Ying,Xiong Xiaofu).计及气象因素的输电线路维修风险分析(Risk analysis method for transmission line maintenance consiidering meteorological factors)[J].电网技术(Power System Technology),2010,34(1):219-222.
[8]Billinton R,Li Wenyuan.Reliability Assessment of Electric Power Systems Using Monte Carlo Methods[M].New York:Plenue Press,1994.
[9]王清印,王峰松,左其亭,等.灰色模糊数学基础[M].武汉:华中理工大学出版社,1996.
[10]Lin Yi,Liu Sifeng.A historical introduction to grey systems theory[C]∥IEEE Internatonal Conference on Systems,Man and Cybernetics,Hague,Netherlands:2004.
[11]吴丹,程浩忠,奚珣,等(Wu Dan,Cheng Haozhong,Xi Xun,et al).基于模糊层次分析法的年最大电力负荷预测(Annual peak power load forecasting based on fuzzy AHP)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2007,19(1):55-58,67.
[12]卜广志,张宇文(Bu Guangzhi,Zhang Yuwen).基于灰色模糊关系的灰色模糊综合评判(Grey fuzzy comprehensive evaluation based on the theory of grey fuzzy relation)[J].系统工程理论与实践(Systems Engineering-Theory & Practice),2002,7(4):141-144.
[13]杨纶标,高英仪.模糊数学原理及应用[M].广州:华南理工大学出版社,2001.
[14]熊兰,刘钰,林荫宇,等(Xiong Lan,Liu Yu,Lin Yinyu,et al).模糊变权法在绝缘子状态综合评判中的应用(Application of fuzzy synthetic method on insulator condition assessment)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2010,22(1):96-100.
[15]李欣然,彭国荣,朱湘有,等(Lin Xinran,Peng Guorong,Zhu Xiangyou,et al).地区配电网建设规模的模糊综合评估方法(Fuzzy synthetic evaluation method of planning size of distribution grid)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2008,20(6):70-77.
[16]谭跃进,陈英武,易进先.系统工程原理[M].长沙:国防科技大学出版社,1999.
