考虑叶顶泄漏的透平级非定常气动性能研究

李少军, 李 军, 龚存忠, 丰镇平

(1中船重工第704研究所,上海 200031;2西安交通大学叶轮机械研究所,西安 710049)

旋转动叶周期性与上下游相邻静叶间相对运动使得叶栅尾迹、叶顶泄漏流以及叶栅通道涡等相互干涉,导致透平机械内部流动具有强烈的非定常特性,进而影响透平机械的气动性能.动叶顶部间隙泄漏流导致的损失在透平总损失的占很大一部分.在非定常条件下,泄漏流形成的泄漏涡与主流掺混后随主流向下游移动并周期性地与下游静叶相互干涉,对下游静叶内部涡系结构的发展及透平的气动性能产生较大的影响.目前对动叶间隙泄漏流的大多数研究都是基于定常分析的,在定常计算时,动静交界面传递的是周向平均量,上游叶片出口的周向不均匀性被完全忽略,与透平的实际运行情况有很大的差别.而进行非定常数值求解时,动静交界面按照时间顺序来传递当地变量,动叶相对于静叶转动至不同位置处的流动特性可以被完全捕捉到,因此可以更好地揭示流场中各种非定常流动细节.

国内外学者对动叶顶部间隙泄漏流动进行了大量的试验和数值研究.Giers等[1]对某低压三级透平动叶围带顶部的泄漏流与主流及下级静叶的干涉作用进行了深入的研究,结果表明:动叶顶部泄漏流所导致的损失中,50%以上是由泄漏流与主流掺混导致的,20%由间隙内的流动损失引起,其余则是攻角损失或二次流损失;Anker等[2]对某一级半低速透平围带顶部的泄漏流动进行了数值模拟,研究了泄漏流对动叶出口气流角和下游静叶攻角的影响;蔡虎等[3]使用自行设计的叶轮机械通用计算程序GAP10对带汽封结构的反动式透平级流场进行了三维数值模拟,分析了汽封泄漏流动进入叶栅通道与主流干涉后的动叶通道流场结构;李军等[4]对汽轮机汽封泄漏流动进行了数值研究.

目前,关于一级半透平级动叶顶部间隙泄漏流与主流非定常掺混的试验测量非常困难,难以捕捉到流场细节,因此通过数值方法来模拟透平级动叶顶部间隙泄漏流与主流非定常掺混的流动细节,对于研究泄漏流动损失的产生和发展机理,提高透平级的气动性能具有重要的工程应用价值.笔者针对所设计的一级半透平,研究了考虑动叶顶部间隙非定常泄漏流动与主流相互作用的流场结构形态,旨在掌握动叶顶部非定常泄漏流动的时空发展和透平级气动性能的变化规律.

1 计算模型和求解方法

表1为一级半透平的几何参数,汽封间隙值为0.25 mm.图1为一级半透平计算域三维网格示意图.计算域采用多块结构化网格,两列静叶采用HOH型网格,动叶采用O型网格,对动叶顶部间隙汽封域进行了多块划分及结构化网格生成,叶顶汽封网格进出口与动叶上端壁处网格采用非完全匹配方式(FNMB)进行联结.壁面第一层网格y+＜10,总网格节点数140万.

数值计算采用商用软件FINE/Turbo来求解三维非定常N-S方程.进口给定总压135000 Pa,进口总温315 K,进气方向为轴向进气,出口给定平均静压101325 Pa,透平转速为4950 r/min.在一个动叶节距内设置30个物理时间步,而在每一个时间步内进行60次内循环迭代计算.计算采用S-A一方程湍流模型,空间差分采用Jameson提出的双时间步隐式时间迭代方法.为加速收敛,首先进行定常计算,再以此定常计算作为初场进行非定常计算.在进行定常计算时采用多重网格,结合变时间步长以及隐式残差光顺方法以加速收敛.在非定常计算结果中选取 T01、T05、T10、T15、T20和 T25六个时刻点进行非定常分析,T01为上一周期80%静叶节距,T05为 0%静叶节距,T10、T15、T20和 T25分别为20%、40%、60%和 80%静叶节距.图2为不同物理时刻动静叶排间的相对位置.

表1 一级半透平级几何参数Tab.1 Geometric Parameters of the one and half turbine stage

图1 一级半透平计算域三维网格示意图Fig.1 Three-dimensional computational g rid of the one and half turbine stage

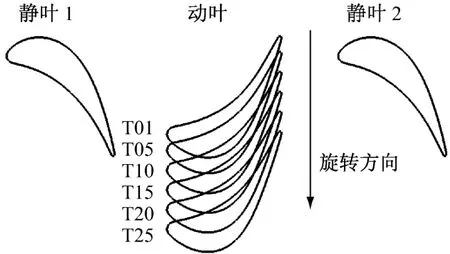
图2 不同物理时刻动静叶的相对位置Fig.2 Relative position of rotor and stator at different phy sical times

2 结果与讨论

2.1 泄漏流的熵变化

由于熵不依赖于任何坐标系,因此在动静叶相互干涉中,熵的分布可以清楚地反映出泄漏流在下游静叶通道中的运动轨迹.图3为第二列静叶85%叶高处的熵分布图.根据不同时刻的熵分布图可以看出汽封出口高熵区域在周向存在不均匀性.T01时刻,在通道中存在两个比较明显的高熵区域A和B,其中区域A为上游动叶汽封泄漏流导致的高熵区域,B为上一周期泄漏流被吸力面前缘所截断在压力面侧形成的高熵区域.随着动叶旋转至不同位置,区域B的流体随主流向下游发展,和主流掺混,其熵值不断减小,并在横向压差的作用下向叶栅吸力面移动,当到达叶栅出口时已发展到占据整个节距通道.区域A的高熵流体熵值从T01时刻起不断增加,在T10时刻时,泄漏流到达静叶吸力面附近,此时泄漏流核心距离静叶前缘最近,泄漏流受静叶前缘堵塞导致熵值升高并达到最大值,随着泄漏流不断冲击到静叶吸力面,动叶顶部汽封出口泄漏流的熵值开始不断减小.

图3 第二列静叶85%叶高处熵分布图Fig.3 Entropy distribution at 85%span of the second stator

在T15时刻,泄漏流被静叶前缘截断成A和B两部分高熵区域,大部分泄漏流冲击至吸力面并在该区域形成堆积,导致吸力面在轴向弦长很大区域内熵值不断增加,高熵值的低能流体在径向压差的作用下向叶栅中叶展方向移动,极大地改变了静叶内上部通道涡的发展,从而改变了叶栅二次涡系结构进而影响气动性能和效率.在T20时刻泄漏流已经全部堆积在吸力面,此时在吸力面狭长区域内熵值达到最大值,在T25时刻随着与通道主流的不断掺混,其熵值开始逐渐减少.

2.2 叶栅出口二次流泄漏流变化

图4为第二列静叶T05和T20时刻三维流线图.从图4中可得到高熵区域的来源以及各种涡系的发展过程.每幅图中标记了五个不同区域的流线来表达出口截面的高损失区域来源.流线1从叶栅上端壁开始发展,形成叶栅上部通道涡;流线2由叶栅下端壁发展而来,形成叶栅下部通道涡;流线3一直延伸到动叶出口截面的高熵区域,为上游动叶尾迹与二次涡系;流线4和流线5从腔室出口而来,为泄漏流形成的泄漏涡.熵增定义:

图4 第二列静叶出口三维流线图Fig.4 3D streamlines at exit of the second stator

式中:Δs为熵增;pref为参考压力;Tref为参考温度;pT和TT为叶栅内任一点的压力和温度;λ为比热常数 ,取1.4.

定义熵函数为e-Δs/R,其中压力和温度取相对值,参考压力和温度取透平进口总压和总温.从熵函数定义可知熵函数为减函数,故熵函数值越大,表示流动损失越小.

图5为动叶和第二列静叶出口110%轴向弦长熵函数沿叶高的分布图.从图5(a)可以看到,泄漏流对动叶栅80%以上叶高损失没有太大的影响,相反在80%叶高以下区域,熵函数变化相当剧烈;在T10时刻和T15,30%叶高区域的损失最大,在T25时刻,该区域损失最小.从图5(b)中也可以得到同样的变化趋势,在第二列静叶出口上端壁熵函数出现小范围的波动,在T05时刻最小,在T20时刻达到最大值,但是远小于40%叶高以下区域的波动,同样在T10时刻,由上游动叶尾迹与二次流引起的损失最大,在T25时刻造成的损失最小.

图5 动叶和第二列静叶出口熵函数分布Fig.5 Entropy distribution at exit of rotor and the second stato r

对比图5(a)和图5(b)发现:当动叶旋转至不同位置时,动叶出口截面熵函数变化较剧烈的为75%叶高以下区域,第二列静叶出口截面熵函数变化较剧烈的为50%叶高以下区域,且在第二列静叶出口截面发生变化的只有上游动叶的尾迹和二次涡系,泄漏流产生的泄漏涡位置和强度基本不变化.

图6为第二列静叶靠近叶片尾缘出口截面的二次流矢量与熵分布图.泄漏流从汽封流出以后,形成与主流垂直的径向流动,径向流动在与主流掺混时有较大的流动损失并形成高熵区域.这部分低能流体在向下游发展时逐渐堆积在第二列静叶吸力面(见图3),在第二列静叶通道中向下游发展并形成泄漏涡,并且在径向压力梯度的作用下向叶片中部移动,最终形成了图6所示的涡系结构.在泄漏流流动过程中,泄漏流出汽封与主流掺混的过程形成较大的损失对后续泄漏流动在第二列静叶出口的流动形态占主导作用.

图6中区域A为逆时针旋转的泄漏涡,区域D对应第二列静叶尾迹在泄漏流的排挤下被推至75%叶高以下区域,并与泄漏流掺混形成的高损失区域.区域E对应第二列静叶的下通道涡与尾迹掺混后形成的高损失区域,由于泄漏流的排挤,该区域更加靠近下端壁.从图6(a)～图6(f)中二次流矢量图可见,下通道涡并没有形成明显的涡旋状态.并且当动叶转动至不同位置时,泄漏涡和上下通道涡的强度和位置并没有发生明显的变化.

图6(a)～图6(f)区域C的熵值变化较为明显,从T01时刻起影响区域不断增大,在T05时刻占据出口截面较大的区域,且熵值较高,在T15时刻后再开始逐渐减少,整个周期内动叶尾迹与二次流的存在区域也只是在60%叶高以下区域.通过以上分析,由于泄漏流的排挤作用,第二列静叶上下通道涡被压制在靠近端壁的狭小区域内,泄漏流虽然对透平的损失和效率影响较大,但是在动叶旋转至不同位置时,其大小和位置却没有太大的变化.因此引起透平效率非定常周期性变化原因是上游动叶尾迹与通道涡二次流的作用.

图6 第二列静叶出口截面二次流与熵分布图Fig.6 The second flow and entropy distribution at exit of the second stator

2.3 第二列静叶脉动速度场

泄漏流的速度远低于主流,因此当气流从相对坐标系进入到绝对坐标系时将会产生速度差异,在相同的横向压差下更容易发生偏转,从而形成由叶片压力面指向吸力面的负射流,在负射流两侧有一对旋转方向相反的涡矢量[5].因此通过分析第二列静叶的脉动速度场可以确定泄漏流产生的涡矢量在第二列静叶中的运动形态.

笔者采用计算模型研究了汽封间隙从0.25～1.00 mm变化时,泄漏流对动叶出口径向相对速度值和相对出口气流角的影响.图7为动叶出口径向相对速度和相对出口气流角沿叶高的分布图.从图7(a)中可以看到,当汽封间隙大小为0.25 mm时,泄漏流产生的径向速度在90%叶高处不超过2 m/s,在60%叶高以下区域的径向速度基本不变;图7(b)中,在85%叶高以上区域不同间隙值形成的泄漏流对出口气流角有较大影响,而在60%叶高以下区域,气流角基本不变.因此随着汽封间隙的变大,泄漏流产生的径向流动速度逐渐增加,且引起主流在叶顶部分的气流偏转也逐渐增加.

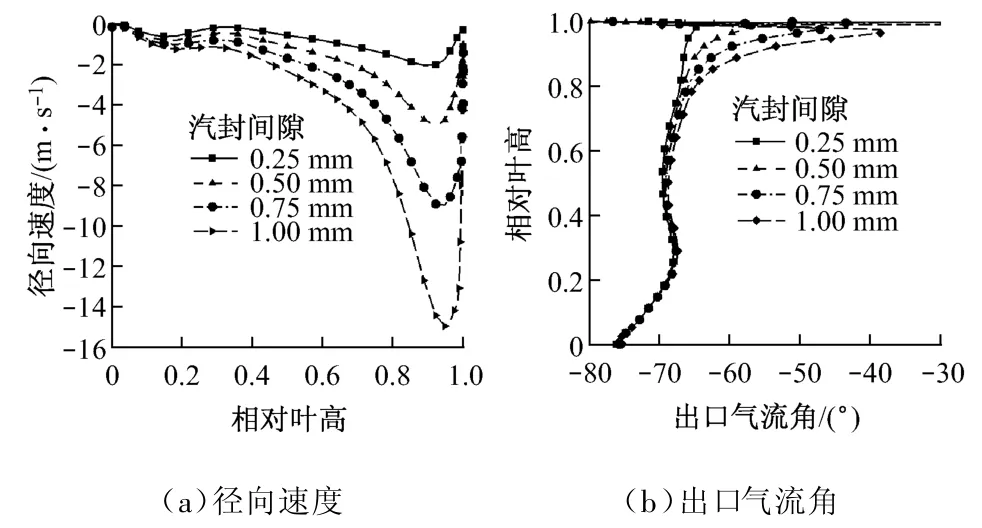
图7 不同间隙下动叶出口径向速度和出口气流角分布Fig.7 Radial velocity and yaw angle at exit of roto r under different clearance conditions

图8为动叶不同叶高处相对速度由于速度差异形成负射流的示意图.图8中U为圆周速度,V为绝对速度,W为相对速度.图8(a)为泄漏流与主流掺混后形成的混合流与主流速度差异形成的负射流,图8(b)为尾迹与主流差异形成的负射流.从图8可以看到,由混合流与主流速度差异形成的负射流强度大小明显大于尾迹与主流速度差异形成的负射流强度.因此形成的对转涡将更加靠近叶栅吸力面.

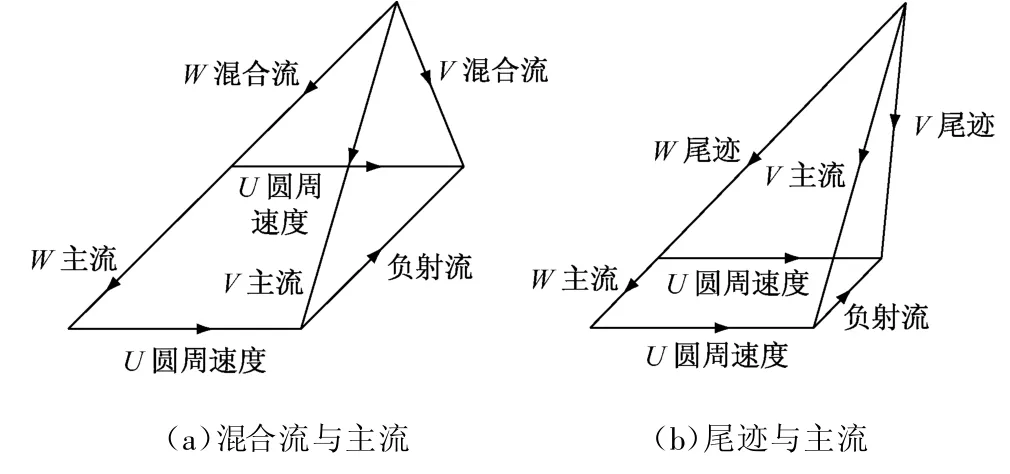
图8 速度差异形成负射流示意图Fig.8 Different velocity triangles

图9为第二列静叶85%叶高处的脉动速度矢量图.在T01时刻,在流道中间有两对旋转方向相反的涡系结构,其中A、B区域的涡为泄漏流产生的两个旋转方向相反的涡矢量,C、D区域的涡为上一周期产生的涡矢量.其中A区域涡矢量逆时针旋转,B区域涡矢量顺时针旋转,箭头方向为负射流方向.区域B中顺时针的涡随着动叶的旋转,其核心不断向静叶吸力面靠拢.从T01时刻至T10时刻,区域B的涡沿吸力面向下游移动,在T15时刻泄漏流移动到叶片吸力面,因而可以看到两个旋转方向相反的涡A、B出现在吸力面附近.从T20时刻起,两个旋转方向相反的涡就一直沿着吸力面向下游移动,在移动过程中与主流不断进行掺混而导致其强度逐渐降低.另外在T20时刻,由于泄漏流已大部分进入叶栅通道且被压制在靠近叶片吸力面一侧,动叶尾迹从泄漏流脱离并进入第二列静叶通道.在区域B的左边,出现一个逆时针旋转的涡系E,对应于第二列动叶的尾迹到达叶片前缘.在 T25时刻,在E的左侧出现一个顺时针旋转的涡系F,对应于动叶尾迹顺时针的涡系.可见,在85%叶高区域,动叶尾迹影响区域和时间都非常有限,泄漏流在该区域起主导作用,对透平气动性能有较大影响.泄漏流对转涡核心区域一直被压制在吸力面附近,影响第二列静叶85%叶高边界层内静压与熵的分布.对比负射流与叶片吸力面的夹角发现:当泄漏流进入静叶通道时,负射流与静叶吸力面有一定的夹角;随着时间的推移,该负射流角度朝垂直于吸力面的方向发生变化,在T20时刻基本与吸力面垂直;而上一周期两个对转涡C、D之间的负射流当动叶旋转至不同位置时基本与叶片吸力面垂直.

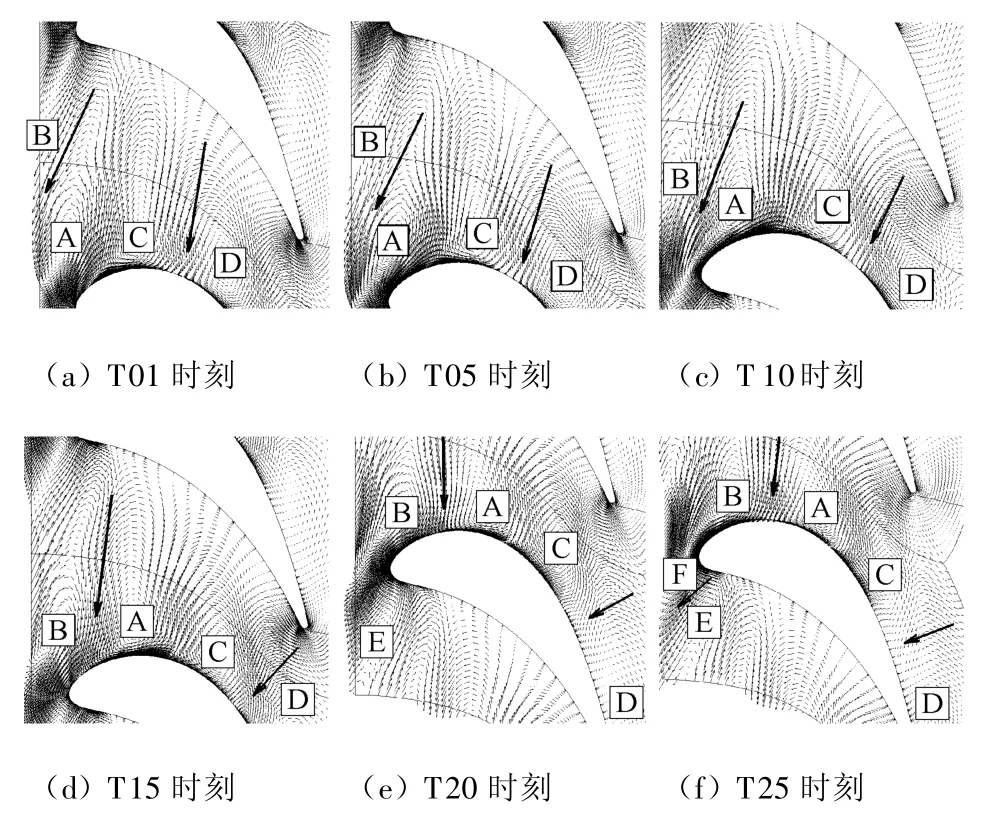
图9 第二列静叶85%叶高处脉动速度矢量图Fig.9 Fluctuating velocity field at 85%span of the second stator

图10为第二列静叶50%叶高处脉动速度矢量图.在50%叶高处脉动速度主要是由动叶尾迹引起的.动叶尾迹产生的对转涡核心基本在主流通道中间,在向下游发展过程中不断与主流进行掺混而使其强度逐渐降低.

2.4 泄漏流对第二列静叶边界层干涉

图10 第二列静叶50%叶高处脉动速度矢量图Fig.10 Fluctuating velocity field at 50%span of the second stator

对透平机械而言,压力是否随时间变化是区分定常计算与非定常计算的主要依据[6].因此寻求气流熵值与压力之间的耦合关系是揭示气流在非定常流场中损失机理的关键[7-8].图11为第二列静叶不同叶高处叶片吸力面第二层网格dp/dt时空图.为方便进行分析,将叶栅吸力面沿弦长归一化处理并作为横坐标,其中0为叶片前缘,1为叶片尾缘;将动叶通过静叶的不同位置进行归一化处理并作为纵坐标,表示通过的时间序列.从图11可以看到,dp/dt呈现周期性的变化,且在叶栅通道的不同位置dp/dt的幅值明显不同.在85%叶高区域,叶栅通道在20%轴向弦长附近dp/dt较大,另外在80%轴向弦长附近同样也出现dp/dt幅值区域,但相比20%轴向弦长附近其幅值较小.在50%叶高区域,dp/dt相比85%叶高处降低了50%左右,并且dp/dt幅值出现在叶片靠近50%轴向弦长附近,在叶栅前缘和尾缘处,也同样存在着波动,但其值相比50%轴向弦长附近要小得多.

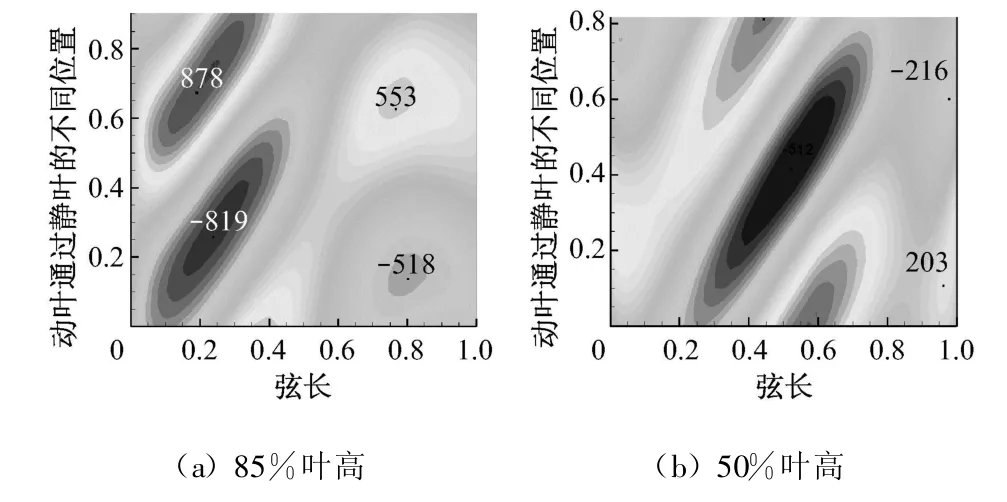
图11 不同叶高dp/dt图Fig.11 Distance-time distribution of dp/dt for blade of different spans

静压波动不仅影响气动性能,对叶栅强度影响也较大.在85%叶高处,由于泄漏流的影响,使较薄的叶栅前缘承受较大的交替变化的压力脉动,极易造成叶栅的变形.而50%叶高处,压力波动出现在叶片较厚的叶栅中部,对叶栅强度的影响比85%叶高处要小.

图12为不同叶高处叶栅表面第二层网格上ds/dt时空图.图12中横纵坐标与图11的一致.从图12(a)和图12(b)中可以看到,ds/dt同样呈现周期性的变化.在85%叶高处,ds/dt在70%和10%轴向弦长附近出现幅值,且在70%附近ds/dt幅值大于10%附近的幅值.在50%叶高处,60%轴向弦长附近也同样出现ds/dt幅值区域,但其 ds/dt比85%叶高处小.由此可见,泄漏流对第二列静叶85%叶高吸力面尾部损失有较大的影响,对吸力面前缘损失影响相对较小,可能是由于在动叶旋转至不同位置时,在85%叶高静叶前缘均存在大量堆积的泄漏流体而导致ds/dt变化较小.

图12 不同叶高ds/dt图Fig.12 Distance-time distribution of ds/dt for blade of different spans

通过对比dp/dt与ds/dt发现,当dp/dt的绝对值增加时,ds/dt的绝对值呈现减少变化.说明压力增加但该区域的熵值却减少.但 50%叶高处与85%叶高处dp/dt与ds/dt幅值的变化规律有所不同.在 85%叶高处,dp/dt较大时,ds/dt较小,两者变化相反;而50%叶高处,dp/dt较大时,ds/dt较大.造成这种现象可能是在不同叶高处引起dp/dt变化的原因不同,在85%叶高处主要是由泄漏流引起;而在50%叶高处主要为势干涉引起的,静压波动导致吸力面边界层内熵值发生波动,且静压波动与熵值波动随时间正相关.

为了进一步说明85%叶高处静压与熵的关系,笔者计算了第二列静叶85%叶高处吸力面沿流动方向上任意两点的静压与熵值脉动图(图13).从图13(a)中可以看到:从上游到下游,静压波动值逐渐减小,且传播方向为从上游至下游.对比图13(a)和图13(b)可以看到,当静压波动值达到极大值时,熵波动值在相应位置上却出现极小值.但当压力脉动峰值较高时(点1),其熵值波动却比较小,当压力脉动值小时(点2),其熵值波动却比较大.

2.5 汽封内部静压波动

图13 85%叶高处不同点压力脉动与熵脉动图Fig.13 Fluctuating curves of pressure and entropy at different points of 85%span

图14为汽封内从进口至出口选取4个不同固定点的压力脉动图.图14中横坐标表示动叶旋转至静叶节距的30个不同位置,通过动叶相对静叶的不同位置表示时间序列,为了方便分析将其进行了扩展一个周期,纵坐标为压力脉动值,脉动压力定义为瞬时压力值和时均压力值之差.从图14可以看出:当动叶旋转至不同位置时,各点压力脉动均呈现周期性的变化规律,且在进口处的压力脉动峰值最小;随着泄漏流向下游发展,各点脉动压力峰值逐渐增大,在出口处其压力脉动峰值最大.箭头方向为压力波动传递的方向,可见在汽封内部,压力传播方向为从下游指向上游,与动叶内压力的传播方向相反.

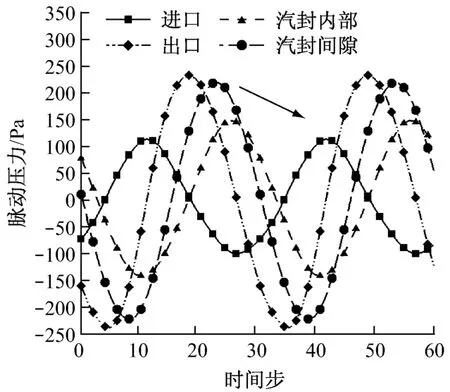
图14 汽封内不同点压力脉动图Fig.14 Fluctuating curves of pressure at different points in gland seal

3 结 论

(1)动叶顶部间隙泄漏流呈现周期性的变化,泄漏流的低能流体到达第二列静叶前缘并堆积,并导致在85%叶高处边界层内dp/dt和ds/dt产生与50%叶高处完全不同的分布规律.

(2)当动叶旋转至不同位置时,在第二列静叶出口截面发生变化的只有上游动叶的尾迹和二次涡系,泄漏流产生的泄漏涡位置和强度基本不变化.

(3)动叶顶部间隙汽封内静压波动呈现周期性的变化,从进口到出口,静叶波动逐渐增加,在汽封内部,压力传播方向从下游指向上游.

[1]GIER J,STUBERT B,BERNAND B,et al.Interaction of shroud leakage flow and main flow in a threestage LP turbine[J].Journal of Turbomachinery,2005,127(4):649-68.

[2]ANKER J E,M AYER J F.Simulation of the interaction of labyrinth seal leakage flow and main flow in an axial turbine[C]//The Porceeding of ASME Conference 2002,Volume 5:Turbo Expo 2002,Parts A and B.Amsterdam,Netherlands,2002,217-224.

[3]蔡虎,朱斌,蒋洪德,等.汽封泄漏流动对透平叶片级通道主流影响的数值研究[J].工程热物理学报,2001,22(3):209-293.CAI Hu,ZHU Bin,JIANG Hongde,etal.Numerical investigation into the interaction between turbine seal leakage and main path flow[J].Journal of Engineering Thermophysics,2001,22(3):209-293.

[4]李军,晏鑫,陈中凯,等.高速旋转的汽轮机隔板密封内流体流动的模拟[J].动力工程,2006,26(3):329-332.LI Jun,YAN Xin,CHENG Zhongkai,et al.Simulation of flow within stepped labyrinth seals of diaphragm in steam turbine under high rotating speed conditions[J].Journal of Power Engineering,2006,26(3):329-332.

[5]MOCZALA M,VON LAVANTE E,PARVIZINIA M.Numerical investigation of loses due to unsteady effects in axial turbines[C]//The Porceeding of ASME Conference 2003,Volume 6:TurboExpo2003,Parts A and B.Atlanta,USA,2003,1029-1037.

[6]YAO Jixian,CARSON S.HPT/LPT interaction and flow management in the inter-turbine space of a modern axial flow turbine[C]∥The Porceeding of ASME Conference 2006,Volume 6:Turbomachinery 2006,Parts A and B.Barcelonan,Spain,2003,1783-1795.

[7]石龑,李少军,邓清华,等.透平级轴向间隙对非定常流动干涉影响的研究[J].西安交通大学学报,2009,43(9):9-13.SHI Yan,LI Shaojun,DENG Qinghua,et al.Study on influence of axial clearance on unsteady flow in turbine stage[J].Journal of Xi'an Jiaotong University,2009,43(9):9-13.

[8]石龑,邓清华,李军,等.一级半轴流式透平的非定常流动干涉与时序效应[J].动力工程,2009,29(2):111-116.SHI Yan,DENG Qinghua,LI Jun,et al.Interaction and clocking effect of unsteady flow in one and half axial-flow turbine stage[J].Journal of Power Engineering,2009,29(2):111-116.