基于近红外光谱的脑立体定向手术导航技术研究

陶 玲 钱志余 朱晓芬

(南京航空航天大学自动化学院，南京 210016)

引言

在脑神经立体定向手术过程中，系统定位精度一般受医学影像质量、定位仪系统误差、注册算法误差和术中脑组织移位等方面的影响[1]。目前，医学影像误差通常不超过1 mm，定位仪系统误差在0.5 mm左右，注册算法误差一般为2～3 mm，而脑组织移位产生的误差对整个系统精度的影响最大，一般为前三者的2～3倍，是影响系统导航精确度的主要因素[2]。如何在手术过程中实时校正脑组织移位带来的实际穿刺路径偏移问题，成为神经外科手术导航系统长期困扰而又面临挑战的难题。

目前，临床解决脑组织移位的主要技术有：微电极导向立体定向技术、超声导航技术、微导管技术以及术中成像技术[3-5]。微电极导向立体定向技术主要依靠经验判定信号特征，没有定量识别参数;超声图像比较模糊，很难识别1 cm以下的组织以及声阻抗很小的脑白质与脑灰质;微导管技术必须在剪开硬脑膜后施行，同样无法解决打开硬脑膜所引起的移位问题;成像技术在监测和纠正脑移位方面比较理想，但其依赖于昂贵的系统设备，对手术器械及手术室的环境有着很高的要求，难以普及推广。近红外光谱技术作为一种对人体无损、无创、无电离辐射的测量手段，其光学参数和医学影像数据存在密切的关联，能够实时微创地获取生物组织内部光学信息，反映组织内部成分和组织功能状态的变化，为实时采集探头前方的脑组织特性实现组织精确定位提供了可能[6-7]。

1 近红外导航辅助原理及关键技术

近红外光是介于可见光和中红外之间的电磁辐射波，穿透力强，能轻易透过头皮、颅骨及其下各层进入脑组织。生物体中不同组织对近红外光具有不同的吸收和散射特性，近红外光对不同的软组织具有较强的区分能力。根据这种特性，可以利用近红外光谱法测量组织的光学参数，从而得到组织的生理信息，或者建立生理信息和光谱数据的关系。相关研究成果表明，近红外约化散射系数与影像灰度信息在组织结构识别方面存在高度相关性[8-9]。显然，如果能找到影像数据和近红外参数之间的关联特性，便可以通过近红外参数来实时引导手术的穿刺，达到实时导航、靶点识别与实时纠错的目的。

基于近红外光谱的手术导航原理如图1所示，其基本思想是：首先通过大量实验数据，获得NIRS数据与MRI影像数据之间的关联特性，建立两者之间的数学转化模型G;在手术计划时，根据患者影像数据TS，建立患者的三维可视化模型S，确定入刺点和靶点，并进行手术路径规划，获得规划的手术路径上的影像灰度信息Dl;然后利用建立的数学模型G，将手术计划路径的灰度信息转换为NIRS参数信息Rl;在手术过程中，利用本课题组开发的fNIRS近红外微创在位连续监测系统和特制的双光纤埋入毁损微创探头，将实时检测到的生物组织穿刺路径上的近红外光学参数信息RN与Rl进行对比，通过近红外导航，实时纠错模型J(α，γ)获得实际路径可能偏离计划穿刺路径的角度α和方向γ，并用 α和γ引导路径的实时纠偏，直到实际的导航穿刺路径RN与Dl的差值在系统误差范围之内。

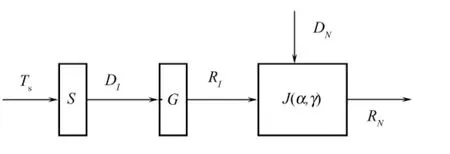
图1 近红外导航原理Fig.1 Schematic diagram of NIRS navigation

显然，影像数据和近红外光学参数之间数学关联模型的建立，以及近红外导航实时纠错方法的研究，是实现近红外手术辅助导航的关键。

2 数学关联模型的建立及验证

2.1 材料与方法

为简化分析，以双层均匀模拟胶为实验对象，模拟人脑内两个不同的组织特性。实验共有32个双层phantom模型，每层模型的厚度均为10 mm，分为上升组和下降组，每组各有16个配比浓度不同的模型。上升组模拟胶模型其下层的约化散射系数μ's2大于上层的约化散射系数 μ's1，下降组模拟胶模型其下层的约化散射系数小于上层的约化散射系数，即 μ's1＞ μ＇s2。

首先，对32个双层phantom模型进行磁共振图像采集，获得各模型矢状位的磁共振结构像。然后，采用生物组织光学参数测量系统，对各phantom模型进行约化散射系数μ's的采集，并对采集到的针道轨迹上的约化散射系数进行平滑滤波等处理，获得约化散射系数随模拟胶深度变化的曲线。图2为上升组中8组模型针道上的光学测量结果，其中不同颜色的曲线代表不同的模拟胶模型。由图2可见，各条曲线0～10 mm为模型上层，μ's值基本保持平稳;10～20 mm为模型下层，μ's值也基本保持平稳。各条曲线在10 mm处，即两层模型的分界处，μ's出现了明显的跳变现象，分层现象清晰可见。值得注意的是，在模型分界处前2 mm左右，即深度为8～10 mm的区域内，曲线提前出现了上升或下降的变化趋势，这个区域为探针的前视距离引起的层间伪影区。通常层间伪影产生的影响主要在模型前一层中，后一层采集到的数据不再受层间伪影的影响。分界层处的伪影会影响探针定位的准确性，需要利用层间伪影消除法进行处理[10]。对伪影消除后的约化散射系数进行统计，获得各层模型约化散射系数的均值。同时，基于模拟胶三维可视化模型，提取近红外微创探头针道轨迹上的灰度信息，各种配比浓度模拟胶的灰度信息gmri和约化散射系数μ's如表1所示。由于篇幅所限，表1中只给出其中的16组模拟胶模型的数据。

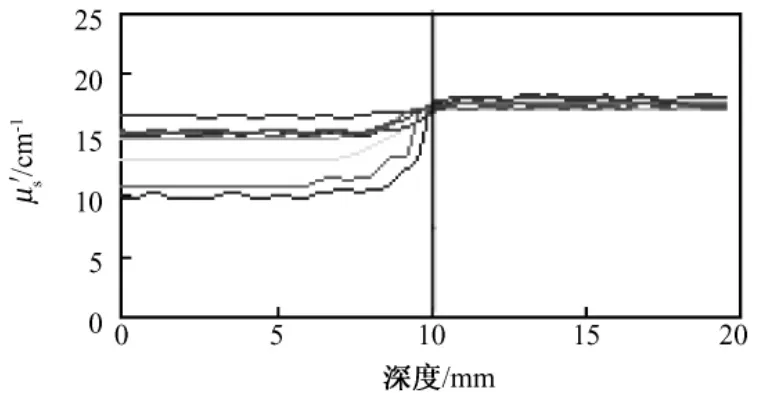
图2 μ's的phantom随深度变化Fig.2 μ's changes plot with the depth of phantom

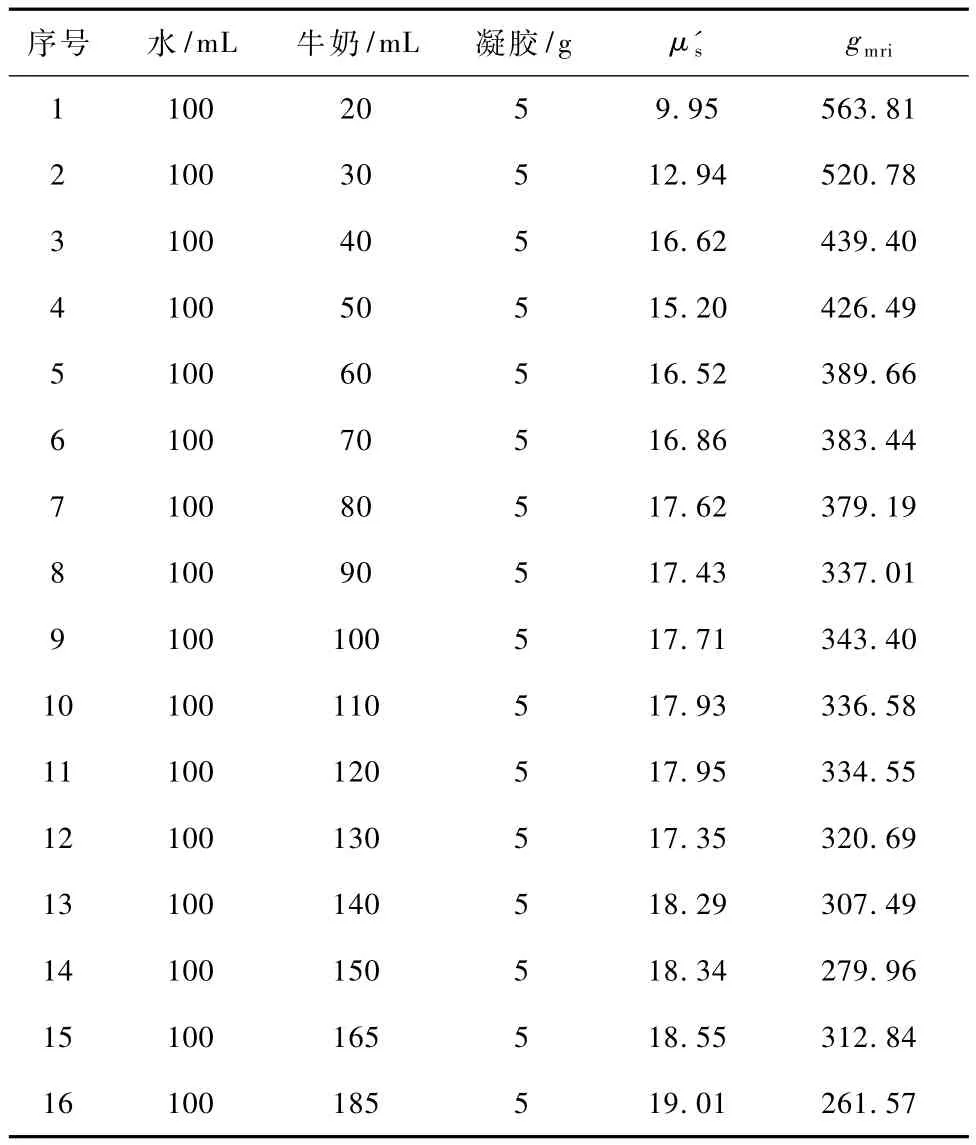
表1 各配比浓度模拟胶的灰度信息和约化散射系数Tab.1 Gray information and reduction scatter coefficient of different concentration phantom

2.2 数学模型的建立

数据处理后的近红外约化散射系数μ's与灰度信息gmri之间的散点如图3所示。

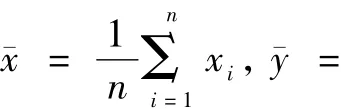
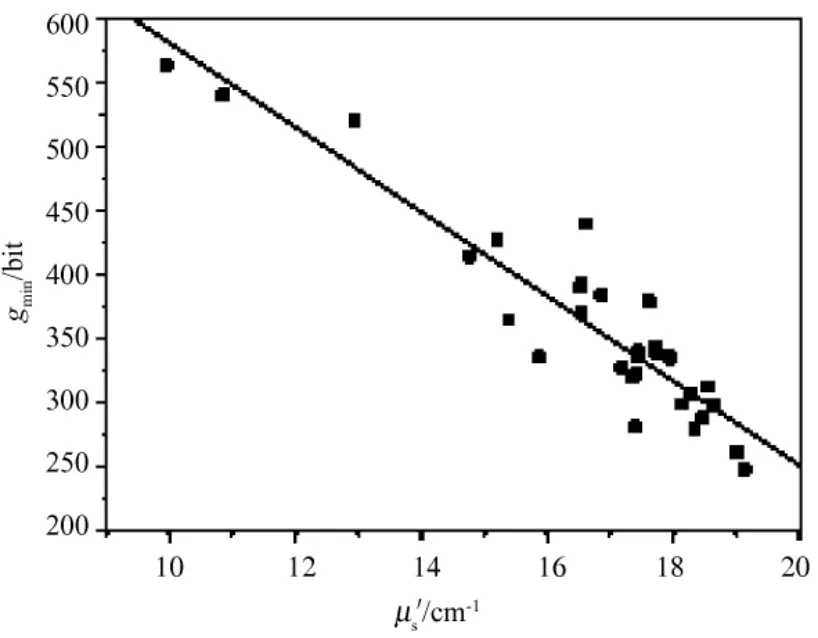
图3 约化散射系数与灰度信息散点Fig.3 Scatter diagram of reduction scatter coefficient and gray information

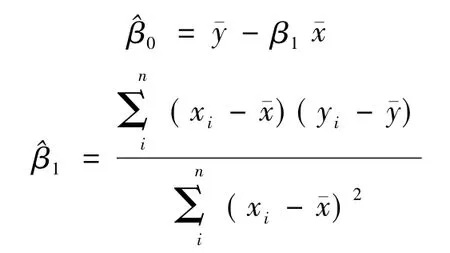
由此得出回归直线的方程表达为

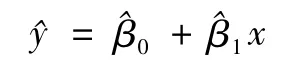
采用肖维勒准则，对表1中约化散射系数和灰度值进行判断，看是否存在异常实验数据[11]。原理如下：对于数据点 vd(x＇μs，ygmri)，若其残差 Vd满足|Vd|＞ ωnσ，其中，ω32=2.42 为肖维勒系数，σ 为标准差，则实验数据点的误差较大，应予以删除;否则，vd应保留。分析结果发现，数据点 vd(16.62，439.40)为异常实验数据，故将其剔除。然后，对表1中的数据进行回归分析，结果如表2所示。由表2中的数据可计算得出：=885.48。

基于上述分析，建立模拟胶近红外光学参数与MRI影像数据的线性回归模型，模型表达式为ygmri=-31.79x＇μs+885.48。其中，x＇μs为近红外约化散射系数，ygmri为影像灰度信息。

2.3 数学模型的验证

表2 灰度信息和约化散射系数统计分析Tab.2 Statistical analysis result of gray information and reduction scatter coefficient

根据表2计算可得：统计量 F=45.107，取置信标准 α =0.05，F0.95(1，31-2)=4.18，显然 F ＞ F0.95(1，29)，表明约化散射系数与灰度信息间存在显著的线 性 关 系，建 立 的 模 型 y"gmri= -31.84 x'μs+888.75的概率为95%，可靠性较高。

为了进一步验证模型的有效性，采取若干组不同配比浓度的phantom模型进行实验，将模拟胶实验数据与数学模型计算所得数据进行比较，发现二者之间有较高的拟合度，说明所建立的模型有高度的可靠性。课题组将模型应用于猪肉等生物组织，也取得了比较高的可靠性。当然，由于模型是在模拟胶实验下获得的，不排除在应用于真实的人体组织时可靠性会降低，但模拟胶的特性和人体组织的光学特性近似，因此模型的线性关系不会改变，后续的工作将采用小动物实验对模型进行修正。

3 基于近红外光谱的路径纠偏

所建立的近红外纠偏模型必须要解决两个方面的问题：其一，手术过程中得到实时路径和计划路径的拟合程度;其二，如果实时路径发生偏差，能实时给出偏差的角度和方向，用于指导实时纠偏。根据患者术前影像资料进行手术路径规划，如图4所示。图4(a)为计划穿刺模型，其中A为入刺点，D为靶点，AD为手术计划路径;图4(b)为计划路径锥形化示意图，ADi(i=1，2，…，n)为手术过程中可能偏移的路径。由于脑组织移位或变形等原因，实际穿刺时的路径可能会存在一定角度的偏移，显然偏离路径位于以 AD为中垂线，α为顶角的圆锥面上。在实际穿刺过程中，入刺点A不会改变，穿刺过程中探头位置T的光学参数信息可以实时获得，将AT光学参数曲线实时与计划路径AD上的光学参数曲线匹配。如果拟合误差在系统误差范围内，则认为实时穿刺过程正确，不需要调整;一旦拟合误差超出系统误差范围，则将AT光学参数曲线实时与偏移路径ADi光学参数曲线拟合，找到和其拟合度最接近的ADi。最后，根据 ADi信息，计算偏离角度α和偏离方向γ。

在手术计划时，建立影像数据计算机空间坐标系，得到AD和ADi空间参数方程;利用三维可视化模型S和三维体数据插值算法，求出 AD和 ADi相应路径上的影像灰度值;再利用数学转化模型G将影像灰度曲线转化成AD和ADi相应路径上的光学参数曲线，用来在术中实时引导路径的纠错。

在计算机空间中，设入刺点坐标为 A(x0，y0，z0)，靶点坐标为 D(x1，y1，z1)，确定以 AD 为中垂线、α为顶角的圆锥底面圆的参数方程为

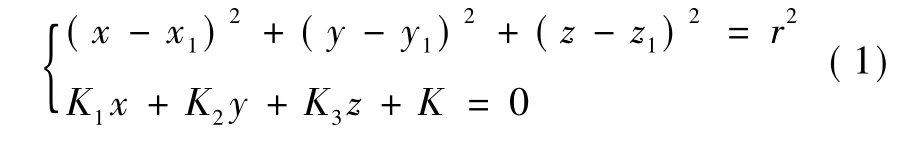
图4 规划路径。(a)计划穿刺模型;(b)计划路径锥形化Fig.4 Schematic of planning path.(a)navigation path model;(b)the coned path

式中，r=|AD|tanα 为空间圆的半径，K1、K2、K3、K为与计划路径AD垂直的平面方程的参数。经计算，式(1)的参数方程为

式(2)确定了α为顶角的圆锥底面圆的参数方程。显然，各偏移路径靶点的坐标必然落在圆锥底面上，由此可以确定对应于偏移角度α的可能偏移路径，获得偏移路径上每一点的坐标值，即可进行偏移路径相对于AD的方向γ和角度α的计算。

一方面，方向γ和角度α的取值影响路径信息匹配结果的精度，γ和α取值越精细，则匹配结果的精度越高;另一方面，AT光学参数曲线与 ADi光学参数曲线的拟合算法也影响着导航的精度。路径发生偏移表现在曲线趋势变化的不一致，因此采用基于曲率的匹配算法进行偏移路径的拟合，计算简便，精度较高，具有平移、旋转不变性等优点;同时，以改进的Hausdorff距离为准则进行匹配结果的验证，避免了个别点对整体匹配的影响，匹配计算仅在少量的特征点集间进行，提高了算法的速度及匹配的精度。有关这部分的算法和实验过程在文献[12]中有比较详细的介绍，这里不再赘述。

4 实验结果及分析

制备不规则模拟胶，在模拟胶实物上表面标记一点，作为手术路径规划的入刺点。采用德国西门子公司的3-Tesla MR对模拟胶的矢状位进行扫描，具体参数设置为：TR=3000 ms，TE=50 ms，FOV=240 mm×240 mm，矩阵尺度512×512，层间距为0，层厚4 mm。基于三维可视化模型和二维图像序列，进行模拟胶计划路径的规划。为简化分析，选取垂直的计划路径，如图5(a)所示，图中两点之间的连线即为计划路径。将计划路径锥体化，将α从1°开始取值(多次实验结果发现，当α在1°以内时，其偏差基本在系统误差范围内)，以 Δα为1°连续变化，在每个α角度对应的圆锥面上每隔10°对应一个偏离方向，记为 γ(α，i)(i=1，2，…，36)，一个 α 对应 36个方向，本系统取了10个圆锥面，一共的偏移路径信息是360个。当然，在实际应用中如要获得更高的精度，可以将γ取得更精细。将获得的若干条偏移路径放入软件数据库，用来在术中实际引导路径的纠错。

模拟胶实物穿刺过程如图5(b)所示，探针从上表面标记的入刺点进入，以不同α角度及其不同方向γ偏离计划路径进行穿刺。在实验过程中，从1°开始取值，每隔2°(Δα=2°)在随机选取的偏离方向进行穿刺，发现本纠错模型给出的偏离方向γ和实际偏离方向完全一致，而给出的偏离角度α在1°～5°之间时存在一定的随机性，在 7°以后趋于稳定，误差不会超过1°，靶点识别误差在1 mm以内，并且在偏移角度13°以后，系统给出的纠偏角度与实际偏移角度完全接近。部分实验数据如表3所示。

图5 模拟胶实验。(a)手术计划路径;(b)实际穿刺路径Fig.5 Schematic of phantom experiment.(a)surgery planning path;(b)real puncture path

表3 路径纠偏结果Tab.3 Result of path correction

在偏移角度较小时，系统纠错信息不稳定，分析其原因可能有：一是设置实际偏移角度时存在误差;二是制备模拟胶时，同层模拟胶较厚，其不规则性不够明显，路径偏移较小时反映在路径信息上的差别较小;三是探头本身存在一定误差。实验结果表明，整个系统可以达到近红外实时导航和实时纠偏的目的，但是纠偏的精度和可靠性问题仍需在后续工作中进一步深入研究。

基于近红外的实时导航技术，具有设备运行安全可靠、定位误差小、导航精度高等优点。当前，在临床应用上较为广泛且技术较成熟的是脑立体定向手术导航系统，所存在的普遍问题是无法克服手术过程中脑组织移位带来的定位误差问题。近红外光谱技术作为一种对人体无损、无创、无电离辐射的测量手段，能够实时微创地获取生物组织内部光学信息、实时采集微创探头前方的脑组织特性、实时发现和纠正脑组织移位带来的误差等，为实现组织精确定位提供了可能，但相关的数学模型以及定位的精度和可靠性还要在大量的生物实验中不断完善。

5 总结

针对脑立体定向手术导航系统中存在的组织移位问题，提出利用近红外光谱技术辅助导航的解决方案。将功能近红外光谱技术与医学图像可视化技术相结合，建立近红外参数信息和影像灰度信息之间的数学关联模型，实现生物组织光学参数识别，从而实时引导手术进程;将影像计划穿刺路径锥形化获得可能的偏移路径的灰度信息作为近红外路径偏移纠正的先验知识，采用曲率匹配的算法对偏移路径进行拟合，并以改进的Hausdorff距离为准则进行匹配结果的验证，达到基于近红外光谱技术的术中移位实时纠错目的，实现误差范围内近红外路径偏移的有效定位。后续工作将进一步补充动物实验，对所建立的关联模型进行验证和完善，同时将针对实际临床数据，不断完善实时路径纠偏模块，整个系统软件的稳定性也有待进一步提高。

[1]Bjartmarz H， Rehncrona S. Comparison of accuracy and precision between frame-based and frameless stereotactic navigation for deep brain stimulation electrode implantation[J].Stereotact Funct Neurosurg，2007，85(5)：235-242.

[2]Dhaese PF，Pallavaram S，Konrad PE，et al.Clinical accuracy of a customized stereotactic platform for deep brain stimulation after accounting for brain shift[J].Stereotact Funct Neurosurg，2010，88(2)：81-87.

[3]Benhaim S，Asaad WF，Gale JT， et al. Risk factors for hemorrhage during microelectrode-guided deep brain stimulation and the introduction of an improved microelectrode design[J].Neurosurgery，2009，64(4)：754-762.

[4]Wagnetz U，Atri M，Massey C，et al.Intraoperative ultrasound of the liver in primary and secondary hepatic malignancies：comparison with preoperative 1.5-T MRI and 64-MDCT[J].American Roentgen Ray Society，2011，196：562-568.

[5]Funatsu A，Kobayashi T，Nakamura S.Use of the kissing microcatheter technique to exchange a retrograde wire for an antegrade wire in the retrograde approach to intervention in chronic total occlusion[J].The Journal of Invasive Cardiol，2010，22(5)：74-77.

[6]胡光霞，钱志余，孙涛等.基于功能近红外光谱技术(fNIRs)的帕金森病大鼠模型脑组织特性研究[J].光谱学与光谱分析，2010，9：2360-2364.

[7]Murkin JM，Arango M.Near-infrared spectroscopy as an indexof brain and tissue oxygenation[J].British Journal of Anaesthesia，2009，103(1)：3-13.

[8]Kondepati VR，Michael HH，Backhaus J.Recent applications of near-infrared spectroscopy in cancer diagnosis and therapy[J].Analytical and Bioanalytical Chemistry，2008，390(1)：125～139.

[9]Ranganatha S， Haihong Z， Cuntai G， et al. Temporal classification of multichannel near-infrared spectroscope signals of motor imagery for developing a brain-computer interface[J].NeuroImage，2007，34(4)：1416-1427.

[10]李韪韬，钱志余，王惠南，等.近红外光纤探头"视距"的组织层模型研究[J].光子学报，2006，35(5)：712-716.

[11]熊艳艳，吴先球.粗大误差四种判别准则的比较和应用[J].大学物理实验，2010，23(1)：66-68.

[12]朱晓芬，陶玲，钱志余.基于近红外光谱的神经导航穿刺路径纠错方法研究[J].生物医学工程学杂志，2010，27(4)：887-892.