MgO-B2O3二元系熔渣质量作用浓度计算模型

王 广，王静松，薛庆国，丁银贵

(北京科技大学 冶金与生态工程学院 生态与循环冶金教育部重点实验室，北京 100083)

我国辽−吉地区蕴藏有大量的硼矿资源，主要包括硼镁石矿和硼镁铁矿两种。自1956年我国硼工业诞生以来，一直开发的主要是较易利用的硼镁石矿，目前该矿的储量已不足200万t(B2O3)，其产量已远不能满足硼工业的需要[1]。据统计，到2010年我国硼矿的缺口将达到74. 5万t[2]。按照硼镁石矿目前的开采速度，几年内将会采完，届时我国硼矿资源将面临严重短缺的局面。为了保证我国硼资源的战略供给，作为硼镁石矿替代资源的硼镁铁矿的开发利用已引起了国家的高度重视。20世纪80年代中期至今，东北大学根据硼镁铁矿的化学组成、矿物结构特点，基于选择性还原的基本原理，提出了“火法”综合利用硼镁铁矿的工艺流程，因其简单、高效而极具发展前景[3]。

“火法”流程中的渣系以MgO-B2O3二元系为主，由于渣系的热力学基本性质尤其是活度对火法冶金过程具有十分重要的意义，因此，MgO-B2O3渣系组元活度的研究一直是致力于“火法”利用硼镁铁矿的冶金工作者的研究重心。一方面，研究者们[4−7]用渣金平衡的方法测定了该二元系中组元的活度，但是由于认识和实验条件的不同，彼此差异较大，至今仍没有取得一致性的结论；另一方面，限于硼镁酸盐热力学数据的缺乏，关于MgO-B2O3渣系的热力学计算模型还是很少见的，仅有CaO-B2O3、FexO-B2O3渣系的计算模型见诸文献，证明了共存理论对含B2O3渣系的适用性[8]。本文作者首次采用热力学数据估算与炉渣结构的共存理论[9]相结合的方法，推导了 MgO-B2O3二元系的热力学计算模型，为我国冶金和硼镁铁矿资源的综合利用服务。

1 MgO-B2O3二元系熔渣结构单元的确定

TOROPOV 和 KONOVALOV[10]采用测量冷却曲线的方法对MgO-B2O3体系进行了相平衡研究，得出该体系存在 3MgO·B2O3、2MgO·B2O3和 MgO·B2O3同分熔化化合物。后来，DAVIS和 KNIGHT[11]对MgO-B2O3二元系重新进行了研究，其结果与TOROPOV 和 KONOVALOV[10]的结论基本相同，只是MgO·B2O3会在988 ℃发生分解。随后，KUZEL和JAHRB[12]合成了 MgO·2B2O3，指出 MgO·B2O3并不存在，而是 2MgO·B2O3和 MgO·2B2O3的混合物。FLETCHER等[13]对CaO-MgO-B2O3三元系在900 ℃时的相平衡进行研究，其结果与 KUZEL和 JAHRB[12]的结论相符。MIYAGAWA等[14]以金属镁和硼酸为原料，经电炉热处理后淬冷，用X射线衍射和矿相分析研究了 MgO-B2O3体系的相平衡关系，亦否定MgO·B2O3的存在，证实 MgO·2B2O3为异分熔化化合物，3MgO·B2O3和 2MgO·B2O3为同分熔化化合物。MUTLUER和TIMUCIN[15]采用DTA对MgO-B2O3体系进行了研究，得出体系内复合化合物的种类与MIYAGAWA 相同，只是 2MgO·B2O3和 MgO·2B2O3分别在 1 146 ℃和 995 ℃发生了分解。DELL和BRAY[16]采用核磁共振研究了 MgO-B2O3体系在偏硼酸盐组成处的相平衡组成，得出在不同的样品制备条件下，均不存在 MgO·B2O3。郎建峰[17]通过采用分析纯的 MgO、B2O3按照 3MgO·B2O3、2MgO·B2O3、MgO·B2O3和MgO·2B2O3中MgO和B2O3的组成比例，在高频感应炉中对上述4种硼酸盐进行了人工合成，经过X射线衍射分析，证明MgO·B2O3是不存在的，进一步证实了前人的研究工作。目前最新的MgO-B2O3二元系相图如图 1所示[18]，主要是采用了MIYAGAWA和MUTLUER的研究结果，也就是说，对于 2MgO·B2O3是同分熔化化合物还是异分熔化化合物还没有定论。在MgO-B2O3二元系相图尚存争议的情况下，本研究中规定 3MgO·B2O3和 2MgO·B2O3可在高温下稳定存在。

图1 MgO-B2O3二元系相图Fig.1 Phase diagram of MgO-B2O3 slag melt

综上所述，本研究确定MgO-B2O3二元渣系在“火法”流程下存在的结构单元包括：Mg2+和 O2−两种简单离子，B2O3一种简单分子，3MgO·B2O3和2MgO·B2O3两种复杂分子。

2 硼镁复合化合物标准反应吉布斯自由能的估算

现有的热力学数据手册中尚无 3MgO·B2O3和2MgO·B2O3两种复合化合物的标准反应吉布斯自由能函数的数据。本研究基于化学中广泛采用的复合化合物标准反应吉布斯自由能的同系线性规律[19]来估算所缺的标准反应吉布斯自由能值。该规律在用盖斯定律来解释时，认为碱性氧化物为离子晶体、酸性氧化物为分子，二者结合生成离子晶体，这与共存理论有很大的相似性，3MgO·B2O3和2MgO·B2O3是离子化合物，只是在由固态向熔态转变的过程中，仅发生物理变化即熔化，而没有发生离子化过程，故化合物中的MgO和B2O3仍紧密结合在一起。由于3MgO·B2O3和2MgO·B2O3的介电常数较大，Mg2+和 O2−间的静电吸引力被削弱而在熔态中保持相对独立，但是它们参与反应时是协同进行的。此外，同系线性规律主要用于硅酸盐矿物、标准态298 K时的标准反应吉布斯自由能的估算，在共存理论的框架内，若将其扩展到高温体系，并不影响它的理论基础，且硼酸盐具有与硅酸盐类似的链状、层状、岛状、架状结构[20]，因此，本研究尝试将其运用到高温硼酸盐熔渣体系。

根据从热力学手册中查得的简单氧化物和单质1 460 ℃时的热力学数据[21]，经计算求得了估算时所用的热力学数据，如表1所列。

根据表1中的热力学数据，将各种钙化合物和与其对应的镁化合物的标准反应吉布斯自由能对应作图，如图2所示。得到拟合直线方程如下：ΔGΘ(Ca salt, 1 460 ℃)=

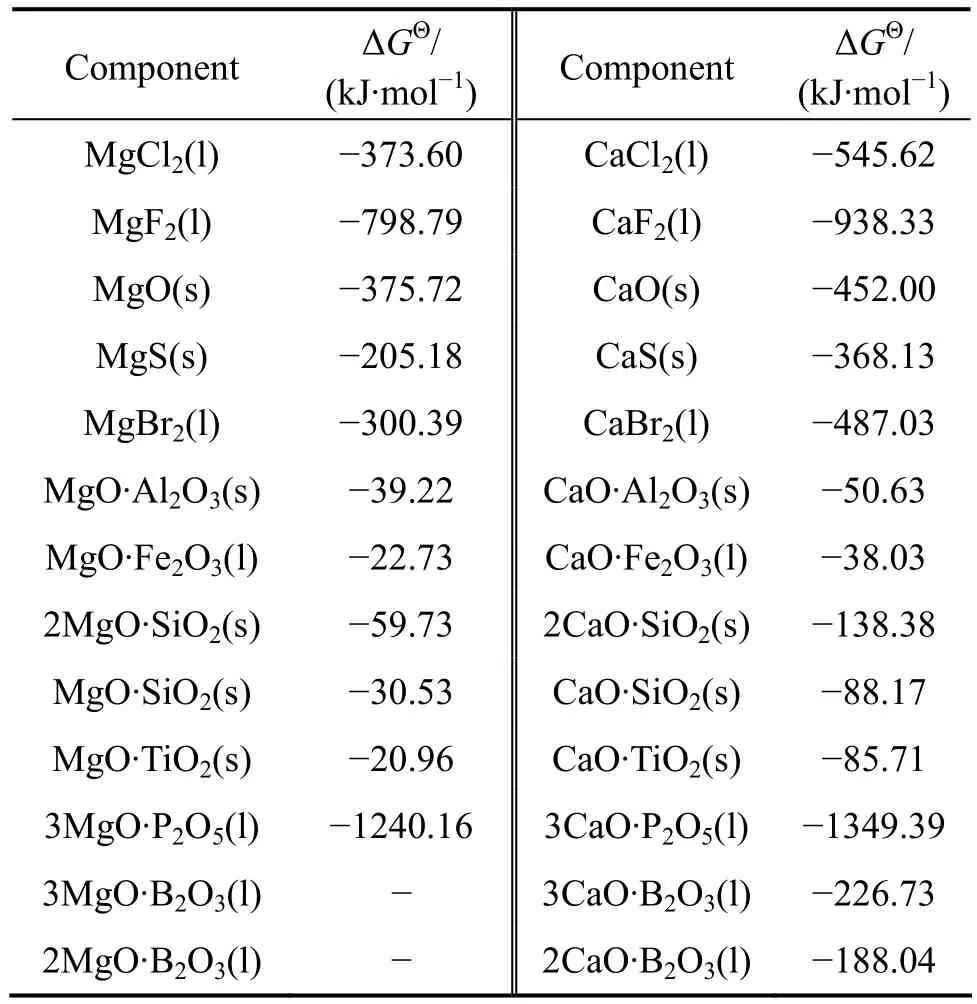
表1 估算硼镁复合化合物1 460 ℃标准反应吉布斯自由能所用参数Table 1 Parameters to estimate standard reaction Gibbs free energy of B-Mg compound at 1 460 ℃

图2 钙盐与镁盐的ΔGΘ间的同系线性关系Fig.2 Linear relationship of standard reaction Gibbs free energy of Ca and Mg salts at 1 460 ℃

1.066 07ΔGΘ(Mg salt, 1 460 ℃)−76.850 19 (1)

其线性相关系数R=0.991 12，可见该方法的可靠性还是比较高的。1 460 ℃时，由 ΔGΘ(3CaO·B2O3)=−226.73 kJ/mol、ΔGΘ(2CaO·B2O3)=−188.04 kJ/mol，根据式(1)可以求得，ΔGΘ(3MgO·B2O3)= −140.59 kJ/mol、ΔGΘ(2MgO·B2O3)=−104.30 kJ/mol。

3 作用浓度计算模型的建立

令各组元的作用浓度为 N1=N(MgO)、N2=N(B2O3)、N3=N(MgO·B2O3)、N4=N(MgO·B2O3)。

同时，令b=∑nMgO，a=∑nB2O3，∑n表示总质点数。

根据物料平衡有

由化学平衡可得

K1、K2分别由 3MgO·B2O3和 2MgO·B2O3在 1 460℃时按K=exp[−ΔGΘ/(RT)]求得的标准反应吉布斯自由能。

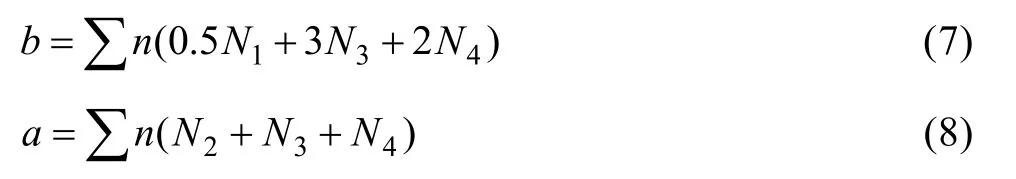
由式(7)和式(8)可得：

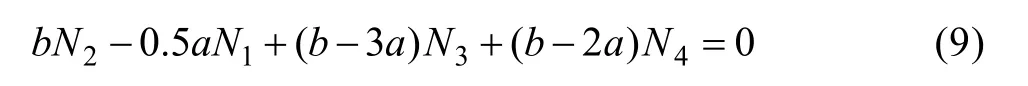
以上式(4)～(6)及式(9)就构成 MgO-B2O3渣系的热力学计算模型，这样N1、N2、N3、N44个未知数有4个独立方程，结合a、b的值，联立求解就可以计算出各组元作用浓度随成分变化的规律。

4 计算结果与讨论

根据 MgO-B2O3二元系相图，1 460 ℃时，在富B2O3区(x(MgO)＜0.45)存在液−液不互溶两相区，该区处于亚稳态，MgO和B2O3的活度在一定温度和浓度区间为与组成无关的恒值。关于该亚稳态区，其边界、最高临界溶解温度、体系的热力学性质等的研究尚不清楚，仅存在较少的实验数据和一些理论上的探讨[22]。在富 MgO 区(x(MgO)＞0.80)，则存在液相与MgO的两相区，此时MgO饱和，其活度为1，其它组分的活度为0。

图3所示为MgO-B2O3渣系各组元的作用浓度在45%＜x(MgO)＜80%组成范围内随炉渣成分变化的情况。从图3中可以看出，1 460 ℃时，由于炉渣中形成了 3MgO·B2O3和 2MgO·B2O3等复合氧化物，导致MgO和B2O3的活度在较大的浓度范围内对拉乌尔定律形成负偏差，其中 2MgO·B2O3和 3MgO·B2O3的作用浓度在靠近其组成处达到最大值。

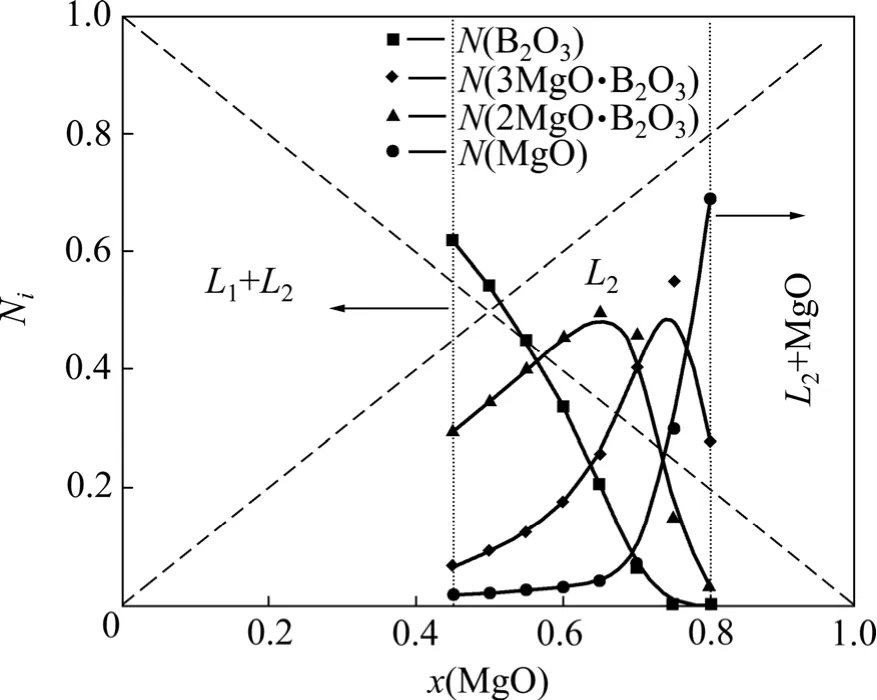
图3 MgO-B2O3渣系各组元的作用浓度随组成的变化Fig.3 Mass action concentration of each component of MgO-B2O3 slag at 1 460 ℃

为了验证模型的计算结果，有必要将理论计算的作用浓度值与实测的活度值进行比较。尽管国内外的学者在不同温度、试验条件以及活度标准态下对MgO-B2O3渣系中MgO和B2O3的活度进行了测定和计算，但是彼此之间差距较大，并没有取得一致性的结论。各文献中所测的MgO-B2O3渣系中B2O3组元的活度如图4所示。

张成弢和冀春霖[4]由于没有考虑MgO和B2O3的挥发，因此平衡问题难以保证[5]。其以原始渣的组成作为最终组成，很可能造成偏差，而且以金属 Sn为溶剂，1 500 ℃下与MgO饱和渣平衡的Mg-Sn合金中Mg的平均摩尔分数仅为0.001 911，这样既难以分析，也较难保证数据的可靠性[7]。

图4 文献中所测的MgO-B2O3渣系B2O3的活度Fig.4 B2O3 activity of MgO-B2O3 slag in different references

戴长虹和张显鹏[5]虽然考虑了MgO和B2O3的挥发问题，但没有进行平衡时间的验证试验。而且其假定1 450 ℃时金属溶剂Cu中的[B]符合亨利定律，然而当温度为1 600 ℃、p(CO)=0.1 MPa时，Cu中[B]的摩尔分数可达 14.5%[6]，已超出了亨利定律的适用范围。所以该文献的数据的可靠性也是难以保证的。

SUNKAR和MORITA[6]以MgO-B2O3二元系相图为基础，找出了液−液不互溶两相区(x(MgO)＜0.34)和MgO饱和相区(x(MgO)＞0.80)与单液相区的分界点，并规定液−液不互溶两相区B2O3的活度为1、MgO活度为0；MgO饱和相区B2O3的活度为0、MgO活度为1，其仅测定了单液相区内数据。体系温度高达1 600℃，而当温度高于1 400 ℃、B2O3的浓度大于0.3时，B2O3的挥发已经使 RAO和 GASKELL[23]研究MnO-B2O3体系热力学性质的试验无法进行。特别是在还原条件下，还会加剧 B2O3以 B2O2形式[24]以及MgO以 Mg蒸汽形式的挥发[5]。而 SUNKAR和MORITA[6]的试验是在石墨坩埚、p(CO)=0.1 MPa条件下进行的，并没有提及防止挥发的措施，所以本研究没有采用其数据。

曹枫等[7]以金属锗为溶剂，提高了镁在锗中的含量，并进行了反应平衡时间的测定。但是其在富B2O3区的液−液不互溶两相区错误地运用G-D方程，进而依据MgO的活度求解了B2O3的活度，以致B2O3活度在富B2O3区仅对拉乌尔定律形成较大的正偏差。考虑到其温度和实验方法的合理性，因此采用他在0.45＜x(MgO)＜0.80区间测量的活度值 α(B2O3)与本研究基于共存理论计算的作用浓度值 N(B2O3)比较，其结果如图5所示。

从图5中可以看出，二者的变化规律是相同的，理论值N(B2O3)与实测值α(B2O3)的拟合程度较高，说明本研究的MgO-B2O3渣系的热力学模型是合理的，该模型在一定程度上能反应MgO-B2O3渣系的实际情况。

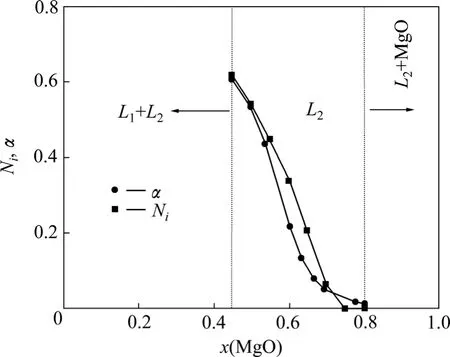
图5 MgO-B2O3渣系理论计算的B2O3的作用浓度与文献[7]中实测活度值的比较Fig.5 Comparison between mass action concentrations and measured activities in Ref.[7]of B2O3 at 1 460 ℃

5 结论

1) 基于复合化合物标准反应吉布斯自由能的同系线性规律估算了所缺的 3MgO·B2O3和 2MgO·B2O3的标准反应吉布斯自由能，并且可信度较高。

2) 推导了 MgO-B2O3二元渣系的热力学计算模型，1 460 ℃时，在浓度为0.45＜x(MgO)＜0.80的范围内，根据模型所计算的 B2O3的作用浓度与实测的B2O3的活度的变化规律是相同的，且拟合程度较高。以MgO-B2O3二元渣系作用浓度模型为基础，在一定程度上可以指导高温条件下MgO-B2O3渣系B2O3活度在特定浓度范围内的准确测定。

3) 对将基于同系线性规律估算复合化合标准反应吉布斯自由能的方法引入到炉渣结构的共存理论，进而解决实际问题的思路进行了有益的尝试，其结果较令人满意。

[1]赵庆杰, 王常任. 硼铁矿的开发利用[J]. 辽宁化工, 2001,30(7): 297−299.ZHAO Qing-jie, WANG Chang-ren. Development and application of paigeite[J]. Liaoning Chemical Industry, 2001,30(7): 297−299.

[2]李文光. 我国硼矿资源概况及利用[J]. 化工矿物与加工,2002(9): 37.LI Wen-guang. The situation of China’s boron resource and its utilization[J]. Industrial Minerals and Processing, 2002(9): 37.

[3]刘 然, 薛向欣, 姜 涛, 张淑会, 黄大威. 硼铁矿综合利用概况与展望[J]. 矿产综合利用, 2006(2): 33−37.LIU Ran, XUE Xiang-xin, JIANG Tao, ZHANG Shu-hui,HUANG Da-wei. Comprehensive utilization of ludwigite and its prospect[J]. Multipurpose Utilization of Mineral Resources,2006(2): 33−37.

[4]张成弢, 冀春霖. MgO-B2O3二元系熔渣中组元的活度[J]. 金属学报, 1989, 25(4): B240−B243.ZHANG Cheng-tao, JI Chun-lin. Activities of components in MgO-B2O3melt[J]. Acta Metallurgica Sinica, 1989, 25(4):B240−B243.

[5]戴长虹, 张显鹏. 含挥发组分 B2O3渣系活度的测定方法[J].金属学报, 1994, 30(6): B243−B246.DAI Chang-hong, ZHANG Xian-peng. A method for measuring activities in slag containing volatile component B2O3[J]. Acta Metallurgica Sinica, 1994, 30(6): B243−B246.

[6]SUNKAR A S, MORITA K. Thermodynamic properties of the MgO-BO1.5, CaO-BO1.5, SiO2-BO1.5, MgO-BO1.5-SiO2and CaOBO1.5-SiO2slag systems at 1 873 K[J]. ISIJ International, 2009,49(11): 1649−1655.

[7]曹 枫, 王之昌, 张 影, 罗志国. MgO-B2O3二元渣的热力学研究[J]. 华东冶金学院学报, 1999, 16(1): 1−4.CAO Feng, WANG Zhi-chang, ZHANG Ying, LUO Zhi-guo.The study on thermodynamics of MgO-B2O3binary slag[J].Journal of East China University of Metallurgy, 1999, 16(1):1−4.

[8]成国光, 张 鉴, 赵 沛. 含 B2O3渣系的热力学计算模型[J].中国有色金属学报, 1997, 7(2): 30−33.CHENG Guo-guang, ZHANG Jian, ZHAO Pei. Thermodynamic calculation models for slag melts containing B2O3[J]. The Chinese Journal of Nonferrous Metals, 1997, 7(2): 30−33.

[9]张 鉴, 成国光, 王力军, 朱 荣, 郭汉杰. 冶金熔体和溶液的计算热力学[M]. 北京: 冶金工业出版社, 2007: 241−245.ZHANG Jian, CHENG Guo-guang, WANG Li-jun, ZHU Rong,GUO Han-jie. Computational thermodynamics of metallurgical melts and solution[M]. Beijing: Metallurgical Industry Press,2007: 241−245.

[10]TOROPOV N A, KONOVALOV P F. Binary system magnesium oxide-boric anhydride[J]. Zhurnal Fizicheskoi Khimii, 1940,14(3): 1103−1109.

[11]DAVIS H M, KNIGHT M A. The system magnesium oxide-boric oxide[J]. Journal of the American Ceramic Society,1945, 28(4): 97−102.

[12]KUZEL H J. Crystal structure of MgB2O4[J]. Neues Jahrbuch für Mineralogie Monatshefte, 1964, 12: 357−360.

[13]FLETCHER B L, STEVENSON J R, WHITAKER A. Phase equilibria in the system CaO-MgO-B2O3at 900 ℃[J]. Journal of the American Ceramic Society, 1970, 53(2): 95−97.

[14]MIYAGAWA S, HIRANO S, SOMIYA S. Phase relations in the system MgO-B2O3[J]. Bulletin of the Tokyo Institute of Technology, 1972, 108: 33.

[15]MUTLUER T, TIMUCIN M. Phase equilibria in the system MgO-B2O3[J]. Journal of the American Ceramic Society, 1975,58(5/6): 196−197.

[16]DELL W J, BRAY P J. The Determination of phase relations in the system MgO-B2O3at the metaborate composition using B11NMR[J]. Physics and Chemistry of Glasses, 1982, 23(4): 100.

[17]郎建峰. 硼铁矿综合利用—关于富硼渣活性的研究[D]. 沈阳:东北工学院, 1991: 17.LANG Jian-feng. Comprehensive utilization of ludwigite—Research on the activity of boron-rich slag[D]. Shenyang:Northeastern University of Technology, 1991: 17.

[18]Verein Deutscher Eisenhuttenleute. Slag atlas[M]. 2nd Edition.Düsseldorf: Verlag Stahleisen GmbH, 1995: 52.

[19]温元凯, 邵 俊. 离子极化导论[M]. 合肥: 安徽教育出版社,1985: 247−280.WEN Yuan-kai, SHAO Jun. Ion polarization introduction[M].Hefei: Anhui Education Press, 1985: 247−280.

[20]袁光辉. 硼酸盐的结构特征及分类研究[D]. 大连: 大连理工大学, 2007: 2.YUAN Guang-hui. Study on the classification and characteristics of borate structure[D]. Dalian: Dalian University of Technology,2007: 2.

[21]梁英教, 车荫昌, 刘晓霞, 李乃军. 无机物热力学数据手册[M]. 沈阳: 东北大学出版社, 1993: 16−449.LIANG Ying-jiao, CHE Yin-chang, LIU Xiao-xia, LI Nai-jun.Thermodynamic data notebook of inorganics[M]. Shenyang:Northeastern University Press, 1993: 16−449.

[22]SUNG S K, THOMAS H, SANDERS Jr. Thermodynamic assessment of the miscibility gaps and the metastable liquid in the B2O3-RO system (R=Mg, Ca, Sr and Ba)[J]. Journal of the American Ceramic Society, 2003, 86(11): 1947−1952.

[23]RAO B, GASKELL D R. The thermodynamic activity of MnO in melts containing SiO2B2O3, and TiO2[J]. Metallurgical and Materials Transactions B, 1981, 12(3): 469−477.

[24]INGHRAM M G, PORTER R F, CAHUPK W A. Mass spectrometric study of gaseous species in the B-B2O3system[J].Journal of Chemical Physics, 1956, 25(3): 498−501.