Mg-Gd-Y-Zr合金热变形本构方程
2011-11-30张新明吴懿萍邓运来唐昌平
张新明,吴懿萍,邓运来,唐昌平
(中南大学 材料科学与工程学院,长沙 410083)
Mg-Gd-Y-Zr合金热变形本构方程
张新明,吴懿萍,邓运来,唐昌平
(中南大学 材料科学与工程学院,长沙 410083)
采用Geeble−1500热模拟实验机测试了高强耐热Mg-6Gd-3Y-0.5Zr合金在变形温度为300~500 ℃、应变速率为10−3~1 s−1下的流变力学行为,采用扫描电子显微镜对其微观组织进行观察,分析了幂函数(PI)、指数函数(EI)和双曲正弦函数(SI)半经验本构方程对该合金变形行为拟合的适用性。结果表明:EI拟合实验结果精度大于PI和SI的,即使对SI函数中材料常数α进行一定优化处理得到SIO函数的拟合精度,也与EI函数十分接近。合金中高温耐热相提高合金高温下的强度是EI拟合优于PI和SI的原因。
Mg-Gd-Y-Zr合金;热压缩变形;本构方程;材料常数优化
高强耐热镁合金在航空航天中应用越来越广泛[1],但镁合金属于HCP结构金属,室温条件下伸长率偏低,塑性加工性能差,故实际应用的镁合金材料大都采用热变形,而流变力学规律与微观组织形成机理是热加工的基础,因而受到广泛关注[2−4]。
研究镁合金热变形行为时,一般使用幂函数、指数函数和双曲正弦函数这3种本构方程对其流变力学规律进行表征。其中,在研究ZK60合金的热压缩变形行为时,本文作者指出在变形温度分别为423 K和423~723 K范围内宜对应采用指数函数和幂函数形式本构方程进行拟合,则两者都能够得到最佳结果[5]。GUO等[6−7]在研究 AZ31合金热压缩流变力学行为时指出,低于 350 ℃下时适合用指数函数拟合,高于350 ℃则适合用幂函数拟合。同时,也有作者指出分别使用幂函数和双曲正弦函数拟合AZ31合金热压缩变形行为时得到的拟合结果相差不大[8]。由上可见,拟合同种ZK60合金的热压缩变形行为时,在不同的变形条件下宜采用不同类型本构方程才能得到各自最佳的拟合结果;在拟合AZ31合金热压缩变形行为时本构方程采用方案也有所不同。不同于ZK和AZ系列合金,Mg-Gd-Y-X系合金高温性能优异[9],热压缩变形时比前两种合金流变应力较大,文献[3, 10]中采用双曲正弦函数拟合该系列合金热变形行为,其中材料常数(α)设为幂函数硬化指数(n)与指数函数硬化系数(β)的比值(α =β/n ),而至今很少有研究涉及对比幂函数、指数函数和双曲正弦函数3种类型本构方程拟合Mg-Gd-Y-X系合金热变形行为时的优劣。
本文作者以一种 Mg-Gd-Y-Zr合金为试验材料,采用幂函数、指数函数和双曲正弦函数3种类型本构方程拟合了该合金热压缩流变行为,综合分析了这 3种函数拟合时的优劣,并对双曲正弦函数的材料常数α进行优化处理以提高其拟合精度。在此基础上,结合组织扫描讨论了本构方程拟合该合金热变形行为不同适应性的微观机理,期望能对揭示Mg-Gd-Y-X系合金的热变形规律提供有益参考。
1 实验
热压缩试验材料为自制铸态Mg-6Gd-3Y-0.5Zr稀土镁合金(简称GW63)。在热压缩前铸锭经过520 ℃、24 h均匀化处理。热压缩试样(d 10 mm×15 mm)用线切割机进行切取。热压缩试验在Gleeble−1500热模拟试验机上进行:变形温度为300~500 ℃,应变速率为10−3~1 s−1,最大真应变为 0.6。热压缩前试样两端涂抹含石墨的固体润滑剂以减小变形时的摩擦。热压缩时1 min内升温到变形温度并保温3 min,以尽量保证试样压缩时温度均匀。所有试样热压缩变形完成后迅速水冷以固定高温变形结束时的显微组织。热压缩变形后的试样沿垂直于压缩轴剖切,经粗磨、精磨、抛光和腐蚀后在 Sirion200场发射扫描电子显微镜下观察微观组织,并分析合金中耐热相成分。根据计算机采集的载荷—位移数据按体积不变原理绘制真应力—真应变曲线。
2 结果及分析
2.1 真应力—真应变曲线

图1 试验合金在不同条件下压缩的应力—应变曲线Fig.1 True stress—strain curves of alloy under thermal compress at different temperatures and strain rates: (a) ε&=10−3 s−1;(b) ε&=10−2 s−1; (c) ε&=10−1 s−1; (d) ε&=1 s−1
GW63合金圆柱形试样热压缩变形的真应力—真应变(σ—ε)曲线如图1所示。从图1中可以看出,变形开始阶段(约ε≤0.05),应力随应变上升很快,但达到峰值应力(pσ)所需应变 (pε)相差很大,各试验条件下pε的范围为0.05≤pε≤0.35。pσ及其对应的应变pε均随温度降低和应变速率升高而增大。当应力达到峰值后,σ—ε曲线分为两类,一类是下降型(D型),即应力开始随应变的增加而不断降低;另一类是稳定型(S型),即应力基本不随应变的增加而增加。σ—ε曲线的D型或S型特征明显受ε&和T的耦合作用,如在应变速率较低(10−3~10−2s−1)的情况下,D 型曲线出现在温度为300~350 ℃;随应变速率升高到1 s−1,温度为400~450 ℃时,σ—ε曲线也转变为D型。
值得特别注意的是温度为 300 ℃、应变速率为10−3s−1时达到峰值应力后,仍能维持稳态变形,但升高应变速率,变形达到峰值应力后试样均失稳断裂。因此,此后计算热变形参数时不考虑温度为300 ℃时的数据以便得到更加精确的拟合结果。
2.2 热变形本构方程
一般金属材料热变形可视为热力学过程,引入变形表观激活能(Q)的概念,热变形的变形温度与应变速率条件可采用带激活能项的 Zener-Hollomon(Z)参数描述(见式(1))。在 σ -ε&-T 作为独立变量的前提下,热变形本构方程有幂函数(式(2))(简称 PI)、指数函数(式(3))(简称EI)和双曲正弦函数(式(4))(简称SI) 3种半经验类型的表征方案,它们均可转化为σ=f( Z)型函数。

式中:σ是流变应力,MPa;R是气体常数,8.314 J/(mol·K); API、 AEI、A 是应变独立因子,s−1;nPI和n是应力指数;βEI是硬化系数;α是应力因子,MPa−1,且 α = βEI/ nPI。
一般认为,PI形式(式(2))适用于低应力水平,EI形式(式(3))适用于高应力水平[11],SI形式(式(4))适用于较宽的应力与应变速率范围[12−13]。然而,应力水平的高低并没有严格的衡量指标,只能依具体情况而定,这就意味着对于同类型合金,有必要对上述3类本构方程函数的适应性进行全面的验证。以下内容将采用上述 3种类型函数分别对实验合金流变行为进行拟合,求解相应的材料常数并进行优劣性验证。拟合数据的范围如下:变形温度为350~500 ℃,应变速率为10−3~1 s−1。
从幂函数(PI)出发,作 l nε&—lnσ 和lnσ—103(RT)−1关系图(见图2),按 QPI= KTKnPI可得应变速率为10−3~1 s−1时各变形温度下的表观激活能QPI,如表1中所列。取表1中 PI下数据的算术平均,得=286.44 kJ/mol。
从指数函数(EI)出发,作 l nε &—σ和σ—103(RT)−1关系图(见图3),按= K K同样可得 TβEI应变速率为10−3~1 s−1时各变形温度下的表观激活能QEI,如表1中所示。取表1中EI下数据的算术平均数,得 QEAI=254.65 kJ/mol。
从双曲正弦函数(SI)出发,按文献[14]中常用的方法,从图2(a)和 3(a)中可得到各变形条件下的 nPI和βEI值,进一步可得到 αSI=βEI/ nPI=0.009 2 MPa−1。图4所示为 l nε &— l n[sinh(αSIσ)]和ln[sinh(αSIσ)]—103(RT)−1关系图,根据=同样可得应变速 率为 10−3~1 s−1时各变形温度下的表观激活能 QSI,如表1中所列。取表1中SI下数据的算术平均数值,得=257.79 kJ/mol。

图2 PI下的 ln ε&—lnσ和lnσ—103(RT)−1曲线Fig.2 l nε&—lnσ(a) and lnσ—103(RT)−1 (b) curves under PI

表1 变形速率为10−3~1 s−1时各变形温度下各本构方程获得的合金的表观激活能QTable 1 Q of alloy at different deformation temperatures and strain rates of 10−3−1 s−1 by using different constitutive equations
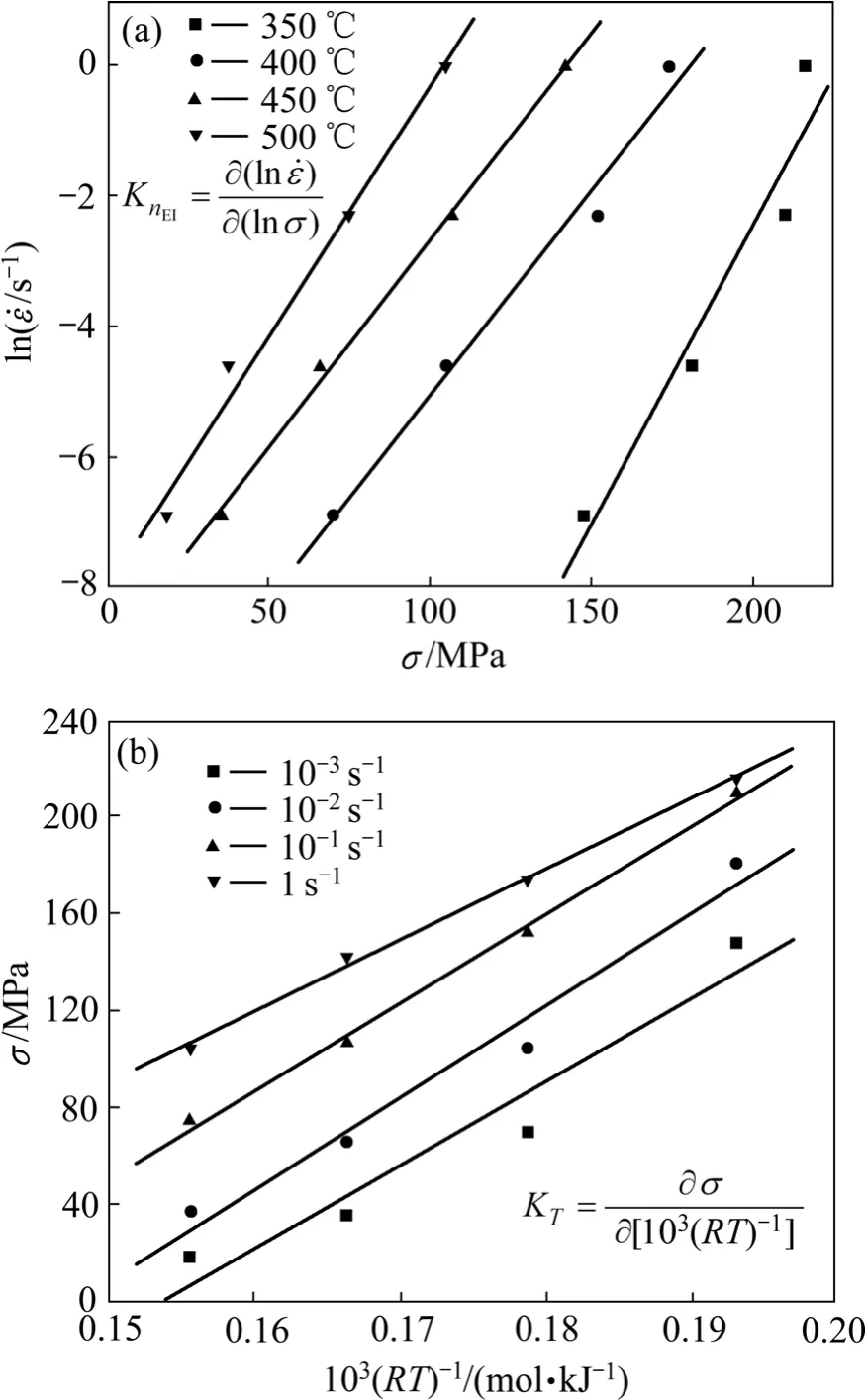
图3 EI下的 ln ε &—σ和σ—103(RT)−1曲线Fig.3 l n ε &—σ(a) and σ—103(RT)−1 (b) curves under EI

图4 SI下 的 l n ε &— l n[sinh(αSIσ)]和ln[sinh(αSIσ)]—103(RT)−1曲线Fig.4 l n ε &— ln [sinh(αSIσ)](a) and ln[sinh(αSIσ)]—103(RT)−1(b) curves under SI
获得上述PI、EI、SI 3个函数所定义的nPI、βEI、αSI以及变形表观激活能 QPAI、 QEAI、 QSAI后,依照式(1)~(4)可进一步求出上述函数中的 API、 AEI、 ASI等材料常数,如图5(a)~(c)所示。图5(a)~(c)的数据点及其线性拟合结果表明,上述3个函数均能建立本研究中GW63镁合金热变形的σ=f( Z)型本构方程。在本研究中,根据式(5)用这些函数预测应力值(σi)与试验值(σPi)间的标准方差(δ)作为判据来检验上述3个函数的拟合精度,计算得δ由小到大的顺序为EI(9.83)、SI(16.78)、PI(44.87)。可见,拟合 GW63合金变形行为时, EI比SI更加接近试验值。EI函数适合在高应力下使用,而 Mg-Gd-Y-X系合金属于高强耐热合金[15−17],因此,这也符合本研究在拟合GW63合金热变形时指数函数(EI)较双曲正弦函数(SI)更加精确的实验事实。

图5 Z与σ的关系Fig.5 Relationship between Z and peak stress σ of alloys under hot compression deformation: (a) lnZ—lnσ; (b) lnZ—σ; (c) lnZ—ln[sinh(αSIσ)]; (d) lnZ—ln[sinh(αSIOσ)]
然而,如图2(a)和3(a)所示,幂函数(PI)中材料常数nPI和指数函数(EI)中 βEI是分别通过lnσ—ln ε &和σ— ln ε &线性拟合得到的,因此,无法对其进行相关数学处理。而 SI中材料常数α是通过关系式α=βEI/ nPI获得,有一定的数学物理基础,可以对α进行优化处理,本研究中采用式(5)对 SI函数中的材料常数α值进行优化,并记优化后的SI为SIO函数。

式中:σi为按式(2)~(4)计算的各ε&—T条件下的应力值;为对应条件下的峰值应力。
在双曲正弦函数中,根据式(5)基于Matlab平台进行编程,通过程序搜索得到最小的δ值为9.17,此时得到SIO函数下的αSIO=0.033 MPa−1,把此值代入SIO函数,则类似可按 QSIO= KTKnSIO得到应变速率为10−3~1 s−1时各变形温度下的表观激活能 QSIO如表1所列,取表中SIO下数据的算术平均值,得252.94 kJ/mol。可由图5(d)求出为 exp33.89,由图可直观看出SIO下的线性拟合误差小于图5(a)~(c)的。
综上可知,在使用PI、EI和SI函数拟合实验合金热压缩变形行为时,由δ检验结果知 EI拟合优于SI。PI、EI与SI对本研究GW63合金的适应性与文献报道的 AZ系列合金的不同,出现这种情况可能与Mg-Gd-Y-X系列合金的高温下强度高有关。在相同的高温变形条件下,该系合金的强度远高于AZ系列合金的,所以,适用于较高应力水平的指数函数(EI)本构方程更加接近实验结果。若对SI函数中材料常数α进行优化处理,则最终δ由小到大依次为 SIO、EI、SI、PI,可见,优化处理对提高双曲正弦函数的精度具有非常重要的意义。本文作者提出的方法(式(5))提高预测精度的效果十分明显,如果不进行材料常数优化,在本研究的试验条件下,双曲正弦函数的精度低于指数函数的精度。
3 讨论

图6 采用各本构方程得到的合金的表观激活能变化趋势Fig.6 Variation trend of apparent activation energies of alloy attained at 350−500 ℃ by using different constitutive equations
在实验数据拟合范围设定为变形温度 350~500℃、应变速率 10−3~1 s−1时,各本构方程下得到的表观激活能变化趋势如图6所示(见表1)。从图6中可以看出,对GW63合金热压缩变形拟合较精确的EI和SIO函数下得到的表观激活能随变形温度变化规律相似,均为先下降后升高,而在拟合性较差的 SI和 PI函数下表观激活能数值则一直呈下降趋势。由于GW63合金中稀土元素Gd与Y的原子半径较大,热压缩后组织中仍然存在富Gd和Y的稀土粒子,如图7及表2所示,使得合金热压缩流变应力处于高应力水平且表观激活能整体数值偏大。同时也看到,EI和SIO函数在变形温度为500 ℃时,表观激活能值升高,这可能是500 ℃变形时多系滑移启动导致的。
拟合AZ和ZK系列合金热压缩流变行为时,文献均指出在较低温度下适合使用指数函数,温度升高适合使用幂函数[5−7]。签于此,本研究中重新将实验数据拟合范围设定为:变形温度400~500 ℃,应变速率10−3~1 s−1,分别使用 PI、EI、SI和 SIO 本构方程拟合实验合金在较高温度下的热压缩流变行为并分析其优劣性。采用式(1)~(5)相同的方法计算得到此时各拟合函数下合金的表观激活能(见表3),δ由小到大的顺序为 SIO(3.58)、EI(5.38)、SI(6.78)、PI(24.05)。由此可见,无论拟合时变形温度范围选为350~500 ℃,还是400~500 ℃,各本构方程拟合优劣性结果一致,均是SIO与EI函数拟合更加接近实验的σ—ε&—T结果。

图7 变形温度为350~500 ℃时合金的SEM像Fig.7 SEM images of alloy compressed at 350−500 ℃: (a) 350 ℃, 10−3 s−1; (b) 400 ℃, 10−2 s−1; (c) 450 ℃, 1 s−1; (d) 500 ℃, 1 s−1

表2 图7(d)中A点第二相能谱分析结果Table 2 EDS results of point A in Fig.7(d)

表3 变形温度为 350~500 ℃和 400~500 ℃时用 PI、EI、SI和SIO得到的合金的表观激活能Table 3 Apparent activation energy attained by PI, EI, SI and SIO at temperatures of 350−500 ℃ and 400−500 ℃
本研究中,指数函数(EI)形式适用于高应力水平的物理意义符合本研究的实验拟合事实,即EI拟合精度优于双曲正弦函数(SI)的。虽然对SI中材料常数α进行优化处理后得到了拟合精度略优于指数函数的SIO函数,然而优化式(5)中α值范围的选定是多次尝试搜索得到的最佳结果,计算过程相对于采用指数函数拟合时更加繁琐。在Matlab编好的程序中,假如输入的α值搜索范围内没有包含能够得到最小δ时的αSIO(0.033 MPa−1)值,那么优化后的双曲正弦函数(SIO)也将得不到比 EI函数更好的拟合结果。因此,拟合GW63合金热压缩流变行为时采用指数函数(EI)最简便且能保证足够的拟合精度。
4 结论
1) Mg-6Gd-3Y-0.5Zr合金中Gd和Y的原子半径较大,合金中高温耐热富稀土相使得合金高温强度整体升高,合金热压缩流变应力较大,得到的表观激活能较高。
2) 拟合 Mg-6Gd-3Y-0.5Zr合金热压缩变形行为时,采用指数函数(EI)本构方程拟合的精度高于幂函数(PI)和双曲正弦函数(SI)的,能得到最简便并与指数函数精度足够的拟合结果。
3) 采用对双曲正弦函数(SI)中材料常数α进行优化处理后的SIO函数拟合实验数据虽然能够得到比指数函数(EI)拟合精度略优的实验结果,但拟合时α取值范围需多次搜索尝试并设定为[SIα/10,10SIα]时才能得到最佳的SIOα值。
4) 变形温度为 350~500 ℃、变形速率为 0.001~1 s−1时,求解得到SIOα=0.033 MPa−1,进而得到采用SIO拟合时合金热压缩变形表观激活能和常数A分别为252.94 kJ/mol和exp33.89。
REFERENCES
[1] 张新明, 彭卓凯, 陈健美, 邓运来. 耐热镁合金及其研究进展[J]. 中国有色金属学报, 2004, 14(9): 1443−1450.ZHANG Xin-ming, PENG Zhuo-kai, CHEN Jian-mei, DENG Yun-lai. Heat-resistant magnesium alloys and their development[J]. The Chinese Journal of Nonferrous Metals,2004, 14(9): 1443−1450.
[2] PRASAD Y V R K, RAO K P. Processing maps for hot deformation of rolled AZ31 magnesium alloy plate: Anisotropy of hot workability[J]. Materials Science and Engineering A, 2008,487(1/2): 316−327.
[3] YANG Z, GUO Y C, LI J P, HE F, XIA F, LIANG M X. Plastic deformation and dynamic recrystallization behaviors of Mg-5Gd-4Y-0.5Zn-0.5Zr alloy[J]. Materials Science and Engineering A, 2008, 485(1/2): 487−491.
[4] YANG Y Q, LI B C, ZHANG Z M. Flow stress of wrought magnesium alloys during hot compression deformation at medium and high temperatures[J]. Materials Science and Engineering A, 2009, 499: 238−241.
[5] GALIYEV A, KAIBYSHEV R, GOTTSTEIN G. Correlation of plastic deformation and dynamic recrystallization in magnesium alloy ZK60[J]. Acta Materialia, 2001, 49(7): 1199−1207.
[6] GUO Q, YAN H G, ZHANG H, CHEN Z H, WANG Z F.Behaviour of AZ31 magnesium alloy during compression at elevated temperatures[J]. Materials Science and Technology,2005, 21(11): 1349−1354.
[7] GUO Q, YAN H G, CHEN Z H, ZHANG H. Elevated temperature compression behaviour of Mg-Al-Zn alloys[J].Materials Science and Technology, 2006, 22(6): 725−729.
[8] FATEMI-VARZANEH S M, ZAREI-HANZAKI A,HAGHSHENAS M. A study on the effect of thermo-mechanical parameters on the deformation behavior of Mg-3Al-1Zn[J].Materials Science and Engineering A, 2008, 497: 438−444.
[9] 肖 阳, 张新明, 陈健美, 蒋 浩, 邓桢桢. 高强耐热Mg-9Gd-4Y-0.6Zr合金的性能[J]. 中南大学学报: 自然科学版,2006, 16(5): 850−855.XIAO Yang, ZHANG Xin-ming, CHEN Jian-mei, JIANG Hao,DENG Zhen-zhen. Performance of Mg-9Gd-4Y-0.6Zr alloy with high strength and heat resistance[J]. Journal of Central South University: Science and Technology, 2006, 16(5): 850−855.
[10] LI L, ZHANG X M. Hot compression deformation behavior and processing parameters of a cast Mg-Gd-Y-Zr alloy[J]. Materials Science and Engineering A,
[11] MCQUEEN H J, RYAN N D. Constitutive analysis in hot working[J]. Materials Science and Engineering A, 2002,322(1/2): 43−63.
[12] LI L, ZHOU J, DUSZCZYK J. Determination of a constitutive relationship for AZ31B magnesium alloy and validation through comparison between simulated and real extrusion[J]. Journal of Materials Processing Technology, 2006, 172(3): 372−380.
[13] SLOOFF F A, ZHOU J, DUSZCZYK J, KATGERMAN L.Constitutive analysis of wrought magnesium alloy Mg-Al4-Zn1[J]. Scripta Materialia, 2007, 57(8): 759−762.
[14] POIRIER J P. 晶体的高温塑性变形[M]. 关德林, 译. 大连:大连理工大学出版社, 1988: 42.POIRIER J P. The plastic deformation of crystals at high temperature[M]. GUAN De-lin, transl. Dalian: Dalian University of Science and Technology Press, 1988: 42.
[15] HE S M, ZENG X Q, PENG L M, GAO X, NIE J F, DING W J.Microstructure and strengthening mechanism of high strength Mg-10Gd-2Y-0.5Zr alloy[J]. Journal of Alloys and Compounds,2007, 427(1/2): 316−323.
[16] YANG Z, LI J P, GUO Y C, LIU T, XIA F, ZENG Z W, LIANG M X. Precipitation process and effect on mechanical properties of Mg-9Gd-3Y-0.6Zn-0.5Zr alloy[J]. Materials Science and Engineering A, 2007, 454/455: 274−280.
[17] 张新明, 陈健美, 邓运来, 肖 阳, 蒋 浩. Mg-Gd-Y-Zr耐热镁合金的压缩变形行为[J]. 中国有色金属学报, 2005, 15(12):1925−1932.ZHANG Xin-ming, CHEN Jian-mei, DENG Yun-lai, XIAO Yang, JIANG Hao. Deformation behavior of Mg-Gd-Y-Zr heat-resistant magnesium alloy during hot-compression[J]. The Chinese Journal of Nonferrous Metals, 2005, 15(12):1925−1932.
Constitutive equation during hot compression deformation of Mg-Gd-Y-Zr alloy
ZHANG Xin-ming, WU Yi-ping, DENG Yun-lai, TANG Chang-ping
(School of Materials Science and Engineering, Central South University, Changsha 410083, China)
Three kinds of constitutive equations, power law (PI), expression law (EI) and sine hyperbolic law (SI) were used to analyze the flow behavior of the Mg-6Gd-3Y-0.5Zr alloy after compression at temperatures of 300−500 ℃ and strain rates of 10−3−1 s−1by using Geeble−1500 test machine. The microstructures were studied using scanning electron microscope (SEM). The results show that EI fits the experimental results better than PI and SI. And even, the sine hyperbolic law with the optimization of material parameter α (SIO) exhibits the close precision to EI. The precipitated heat-resisting phase after compression is the reason for EI better fitting than PI and SI.
Mg-Gd-Y-Zr alloy; hot compression deformation; constitutive equation; material parameter optimization
TG146
A
1004-0609(2011)12-2987-08
国防预研基金资助项目(51312010503)
2010-11-12;
2011-04-08
张新明,教授,博士;电话:0731-88830265;E-mail: wuyipingjia@126.com
(编辑 李艳红)
