高频地波雷达电离层杂波统计特性研究

尚 尚 张 宁 李 杨

(哈尔滨工业大学电子工程技术研究所,黑龙江哈尔滨150001)

1.引 言

高频地波雷达能够对大范围、远距离的海面和低空目标进行实时探测,同时可以对专属经济特区(EEZ)进行全范围的监测,是一种理想的早期预警雷达[1]。高频地波雷达沿水平方向发射垂直极化电磁波,但由于发射天线阵的非理想性,除了绝大部分能量沿海面传播外,还有一部分能量向上发射,被电离层反射后又被非理想的接收天线阵接收,形成电离层杂波[2]。

电离层杂波严重影响了高频地波雷达的探测性能,当电离层干扰强烈时,可能完全淹没100 km以上的全部目标信号[3]。为深入了解电离层杂波对雷达的影响,国内外研究人员对电离层杂波的特性展开了很多研究。文献[2]从距离、多普勒、方向等方面对电离层杂波的特点进行了分析,指出电离层杂波污染的距离取决于反射电磁波的电离层高度;不同层反射的电磁波产生的多普勒频移不同,E层电离层杂波多普勒频移较小、F层相对较大;大部分电离层杂波无方向性或方向性不强。文献[4]对电离层杂波的方向性进行了更为详细的分析,指出电离层杂波可分为两类,一类是镜像反射杂波,一类是扩展杂波,其中镜像反射杂波占据较少的距离元和多普勒元,而扩展杂波能在距离和多普勒上有大的扩展;同时,镜像反射杂波在同一距离元上的不同多普勒元没有方向的相似性,而扩展杂波却呈现了方向的相似性。文献[5]指出占据较少距离元的电离层杂波具有一致性的方向性,而占据较多距离元的电离层杂波则不具有。文献[6]分析了北极圈内 Es层电离层杂波对高频地波雷达的影响,给出了北极圈内Es层杂波随季节、时间的变化情况。另外周浩等对电离层杂波的时频特性进行了分析[7]。

从统计特性角度对电离层杂波进行了分析,利用高频地波雷达的实测数据分别计算了各层电离层杂波幅度统计模型,并对电离层杂波信号的距离相关性、时间相关性进行了分析。

2.高频地波雷达中电离层杂波

2.1 电离层杂波的产生

由于高频地波雷达发射天线的非理想性,有一部分能量没有沿水平方向传播而是向上发射,经过电离层的反射后被接收天线接收形成电离层杂波。为了说明电离层杂波与电离层本身结构特性的关系,考虑简单的情况,假设电磁波垂直入射电离层,同时忽略电子同离子、分子之间的碰撞效应和地磁场,折射指数为

式中:f为入射电磁波频率;f p为等离子体频率,且有

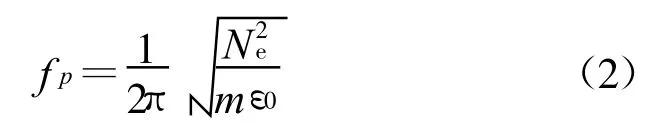
Ne为电子浓度,m为电子质量,ε0为真空介电常数。当一定频率的电磁波进入电离层后,随高度的增加,如果电子浓度增大,则折射指数减小。对于假设的垂直入射情况,当μ=0时,发生全反射[8]。可见电离层杂波的产生与载波的频率、电离层的电子浓度密切相关,当电磁波频率固定时,电离层对电磁波的反射情况取决于电离层电子浓度的平方根。而电离层杂波具有多径效应,使其相当于多个随机分量的叠加。

2.2 电离层杂波的多普勒频移

雷达发射的电磁波被运动目标反射时,接收到的电磁波会产生多普勒频移。电离层本身存在等离子体漂移,同时由于电离层电子浓度时刻变化,使得电离层对电磁波的反射高度也随时间变化,这就使得电离层对于雷达而言是一个复杂的运动目标,产生多普勒频移及多普勒展宽。文献[9][10]指出电离层对电磁波频率的影响可分为电离层运动和电子浓度变化两部分。

假设电离层结构不变时,由电离层本身运动产生的多普勒频移 f dv为

式中:f 0为电磁波频率;c为真空中光速;V为电离层垂直向上匀速运动的速度。

假设电离层反射高度h r与电离层下边界高度h0不变,同时忽略地磁场和碰撞频率的影响,多普勒频移 f dμ与电子浓度 N e的关系为

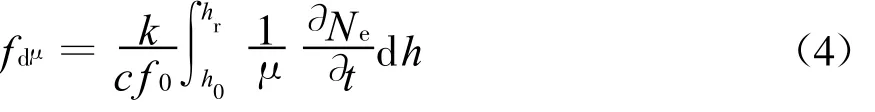
式中常数k≈80.6。

由于电离层不均匀体对入射的电波信号有散射作用,所以电离层反射的信号是由包含振幅与相位都按随机分布变化的波元的波束组成。由于散射信号的存在,当以单一频率w0入射到电离层时,反射信号的频谱将包含有随机信号的多个频率分量,于是单一的信号谱被展宽[8]。

图1是典型的高频地波雷达回波的距离-多普勒谱,其中电离层杂波覆盖了第90个以上几乎所有距离元,并且在含有电离层杂波的距离元上污染了几乎所有多普勒单元。

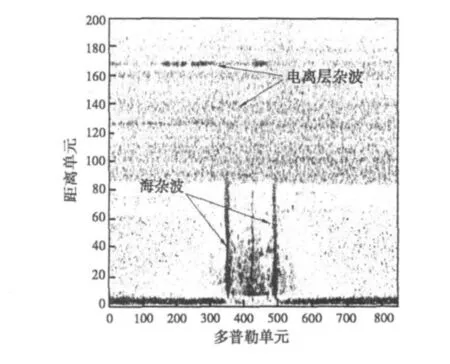
图1 雷达回波距离-多普勒谱

3.回波预处理

高频地波雷达的回波中除了目标信号外,还包含海杂波、地物回波、电离层杂波、噪声等。图2是典型雷达回波的多普勒谱。其中海杂波强度大,对电离层杂波特性分析影响大。

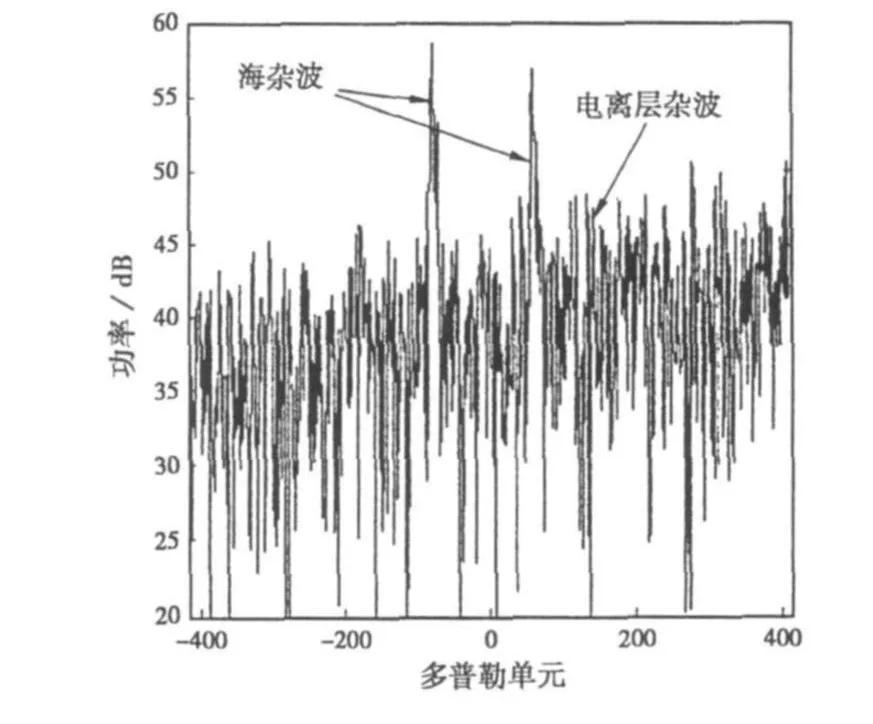
图2 高频地波雷达回波

为了减小海杂波对电离层杂波统计特性分析准确度的影响,采用基于特征值分解的方法对时域信号中海杂波成分进行抑制[11]。实现步骤如下所示:

1)构造时域信号s(n),n=1,2,…,N的Hankel矩阵 H:

式中:N为信号长度;C为欲分解的频率数,N＞C.

2)对H进行奇异值分解:

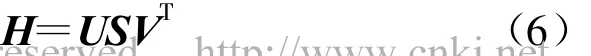
式中

且U、V包含相应的左右特征向量。

3)海杂波频率对应的特征值往往非常大,将S中与海杂波对应的特征值置零后得到S1,重新构造Hankel矩阵H1:

图3为采用特征值分解方法抑制海杂波后的多普勒谱。

图3 抑制海杂波后

4.电离层杂波实测数据统计特性分析

高频地波雷达中的电离层杂波受地理位置、时间、季节、太阳活动、雷达天线垂直方向控制水平、地磁场等诸多因素影响,同时电离层杂波含有多路径分量。雷达回波为时序复数信号,其幅度由实部和虚部平方和决定。对某一含有电离层杂波的距离元在抑制海杂波之后的数据进行分析,图4中的(a)、(b)分别是其实部与虚部的直方图,实线为正态拟合曲线。采用图检验法对上述数据进行正态检验,按规定方法绘制在正态概率纸上,如果接近一条直线则接受其分布为正态分布的假设,结果如图4中的(c)、(d)所示。

由图4可以看出,电离层杂波信号的实部和虚部在正态概率纸上基本是一条直线,即可以接受它们分布为正态分布的假设。

两个独立高斯随机变量的平方和的平方根为Rayleigh分布,所以电离层杂波的幅度应符合Rayleigh分布[12]。Rayleigh分布的概率密度函数为

式中σ为Rayleigh分布参数,其期望和方差分别为

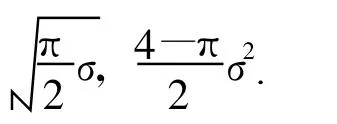
那么Rayleigh分布的标准差与期望的比值η为

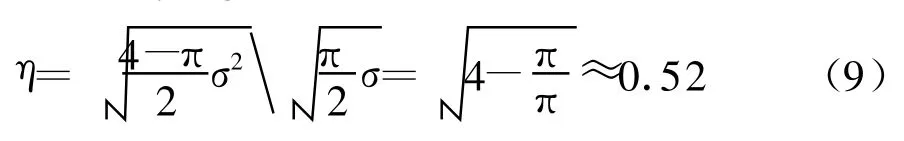
若随机变量符合Rayleigh分布,则其标准差与期望的比值应约为0.52。表1为图1中实测数据抑制海杂波后的电离层杂波在不同距离元上的标准差与均值的比值η,可以看出在大部分距离元上的电离层杂波幅度的η值都趋于0.52,说明大部分距离元上的电离层杂波都基本符合Rayleigh分布。

表1 实测数据η

对不同批次500个距离元上的电离层杂波进行统计,其η值在0.48～0.53之间的电离层杂波数占58%,η在0.55～0.6之间的占30%,大于0.6的占12%,可见绝大多数距离元上的电离层杂波服从或近似服从Rayleigh分布,约10%左右的电离层杂波与Rayleigh分布差异较大。图5中实线是表1中第100个距离元电离层杂波归一化幅度的积累分布曲线,虚线是Rayleigh分布曲线,可见实测数据和Rayleigh分布曲线几乎完全重合。综上,大部分电离层杂波幅度符合Rayleigh分布。

图5 电离层杂波幅度统计分布

但是由前文对电离层杂波的多普勒频移的分析可知,电离层杂波的多普勒频移和展宽与电离层的运动、电子浓度起伏和多径效应等因素有关,这些因素的各个参数随时间和距离不断变化,所以造成某些距离元上电离层杂波呈现非瑞利分布的情况,如表1中第150个距离元。这时,电离层杂波更接近多参数概率分布。

K分布多用于描述草地、树等地杂波和微波波段海杂波[12],这里对于多参数概率分布只考虑Weibull和 Log-normal分布。对表1中η值大于0.6的电离层杂波数据的分布率进行分析。图6(a)中实线是第150个距离元电离层杂波实测的经验累积分布曲线,虚线是参数为(0.31,1.34)的Weibull分布,点划线和“+”线分别是参数为(-1.6,0.89)的Log-normal分布和参数为(0.25)的Rayleigh曲线。图6(b)、(c)分别是表1中第120和第160个距离元上电离层杂波的经验累计分布曲线。从图6中可以看出,电离层杂波功率幅度与Weibull累计概率分布曲线可以很好的吻合,而Log-normal分布与实测数据有较大差距。所以认为由于电离层参数实时变化或突发E层(Es层)等因素造成的非瑞利分布电离层杂波谱幅度符合Weibull分布。

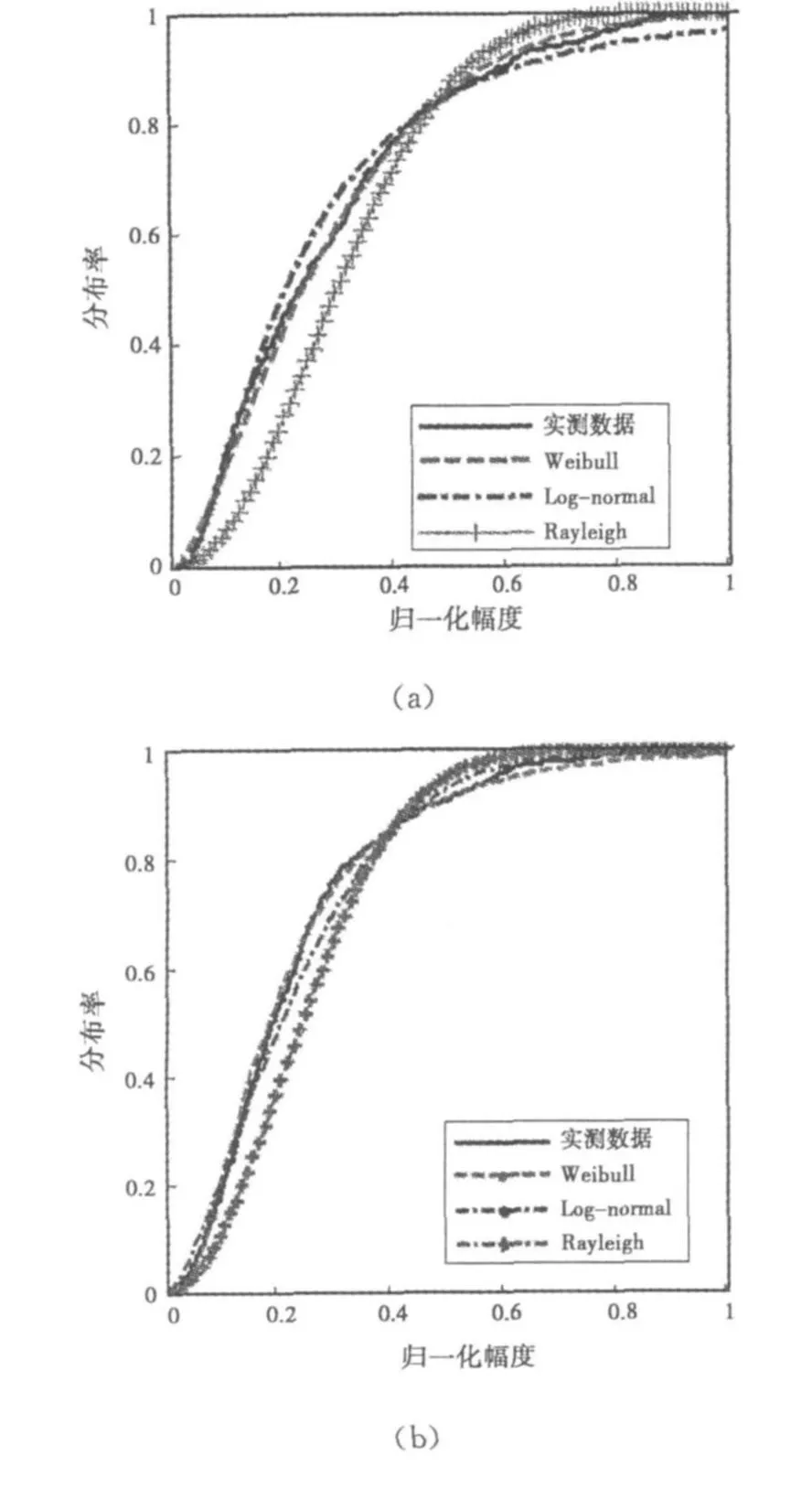
图6 电离层杂波功率谱幅度积累分布

5.电离层杂波的相关性研究

5.1 时间相关性

时间相关性往往是指同一个雷达分辨单元上杂波在时间测量上表现出的相关特性。图7是同一个距离元上电离层杂波的相关系数随时间的变化曲线。

70年的时间，路虎为自己成就了一本充满了精彩故事、不凡车型的画册。而这本画册自此开始，又要翻开全新的一页了。

图7 时间相关特性

在没有电离层爆时(电离层相对稳定时),同一距离元上的电离层杂波相关系数在0.1到0.6之间浮动,而且从实测数据中看,电离层杂波的时间相关系数随时间频繁波动,可见电离层杂波对于雷达系统而言是一个变化较快的时变量。对于舰船等需要长相干积累时间检测的目标,电离层杂波的影响更大。

5.2 距离相关性

距离相关性是指在不同的距离和方位分辨单元上杂波相互之间的关联特性。

图8是电离层杂波相邻距离的相关系数随距离的变化曲线,从图8中可以看到,电离层杂波相邻距离的相关性很强,但是在115和148个距离元处出现了突变点,从电离层结构及其对电波的影响可认为突变点的产生主要有以下两个原因:

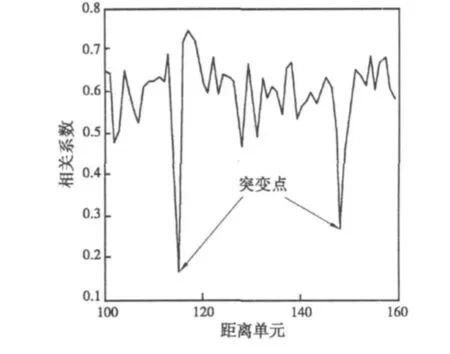
图8 距离相关特性

1)电离层电子浓度的Chapman分布特性

由文中式(4)可知电离层杂波的特性与电离层的电子浓度有关。电离层中电子浓度的分布由电子产生率、损失率和输运过程确定。若暂不考虑输运过程,垂直高度上电子浓度分布如下所示

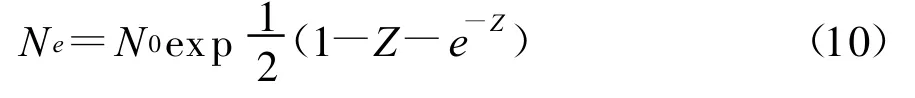
2)电离层中的不规则体

根据湍流理论,电离层中存在明显的界面或者“壁”。在这些“壁”之间,粒子流快速地运动着,在“壁”附近粒子被减速,于是粒子流引起了湍流,从而激起电离层中的不均匀体[8],其中包括突发E层使得电离层杂波相邻距离元的相关系数在某些距离元处出现突变。

图9 电离层电子浓度Chapman分布

6.结 论

通过对高频地波雷达回波数据及电离层杂波产生机理的分析,对电离层杂波的统计特性进行了研究。发现电离层杂波幅度统计特性一般情况下服从Rayleigh分布,但是由于电离层自身结构和多路径等影响因素,某些距离元上电离层杂波呈现非瑞利特性,此时Weibull分布可以很好地描述其分布特性。

分析了同一距离元上电离层杂波相关系数随时间的变化规律,电离层杂波的时间相关性变化较快,说明即使在没有电离层爆时,电离层杂波也是时变的。相邻距离元上的电离层杂波具有很高的相关性,但是在某些距离元上会出现“突变点”。通过对电离层结构特性及其对电磁波的作用分析,可知相关系数的突变与电离层的电子浓度分布特性和其中不均匀体的分界面有关。本文的工作为更好地抑制电离层杂波提供了依据。在特征分解、波束形成等电离层杂波抑制方法中,充分利用电离层杂波的时间相关性和距离相关性来构造杂波协方差矩阵,可以在时域、距离域、多普勒域得到更好的抑制效果。

[1] SEVGI L,PONSFORD A,CHAN H C.An integrated maritime surveillance system based on high-frequency surface-wave radars.Part1:Theoretical background and numerical simulations[J].IEEE Antennas and Propagation M agazine,2001,43(4):28-43.

[2] CHAN H C.Characterization of Ionospheric Clutter in HF Surface-Wave Radar[R].Canada:Defense Research Devlopment Canada-Ottawa,2003.

[3] 沈 伟,文必洋,李自立,等,高频地波雷达的电离层杂波识别新试验[J].电波科学学报,2008,23(1):1-6.

SHEN Wei,WEN Biyang,LI Zili,et al.Ionospheric measurement with HF ground wave radar system[J].Chinese Journal of Radio Science,2008,23(1):1-6.(in Chinese)

[4] WAN X,XIONG X,CHENG F,et al.Experimental investigation of directional characteristics for ionospheric clutter in HF surface wave radar[J].Radar,Sonar&Navigation,IET,2007,1(2):124-130.

[5] JIANG Wei,DENG Weibo,SHI Jialin.Characteristic study of ionospheric clutter in high-f requency over the horizon surface wave radar[C]//IEEE Youth Conference on Information Computing and Telecommunication,Beijing.China,September 20-21,2009.

[6] THAYAPARAN T,MACDOUGALL J.Evaluation of ionospheric sporadic-E clutter in an arctic environment for the assessment of high-frequency surfacewave radar surveillance[J].IEEE Transactions on Geoscience and Remote Sensing,2005,43(5):1180-1188.

[7] 周 浩,文必洋,吴世才.高频地波雷达中电离层杂波的时频特征[J].电波科学学报,2009,24(3):394-398.

ZHOU Hao,WEN Biyang,WU Shicai.Time-frequency characteristics of the ionospheric clutters in high-f requency surface wave radars[J].Chinese Journal of Radio Science,2009,24(3):394-398.(in Chinese)

[8] 熊年禄,唐存琛,李行健.电离层物理概论[M].武汉:武汉大学出版社,1999.

[9] 龙咸灵,侯杰昌.关于电离层反射电波频率变化的问题[J].地球物理学报,1979,22(4):387-395.

LONG Xianling,HOU Jiechang.On the frequency variation of radio waves reflected from the ionosphere[J].Chinese Journal of Sinica,1979,22(4):387-395.(in Chinese)

[10] 黄昌理,乐子华.对“关于电离层反射电波频率变化的问题”一文的意见[J].地球物理学报,1982,25(4):387-390.

HUANG Changli,LE Zihua.Comment on the paper“on the frequency variation of radio waves reflected f rom the ionosphere”[J].Chinese Journal of Sinica,1982,25(4):387-390.(in Chinese)

[11] POON M W Y,KHAN R H,LE-NGOC S.A singular value decomposition(SVD)based method for suppressing ocean clutter in high frequency radar[J].IEEE Transactions on Signal Processing,1993,41(3):1421-1425.

[12] 吴雄斌,尹 微.宽波束高频雷达海洋回波的统计特性[J].电波科学学报,2006,21(3):432-436.

WU Xiongbin,YIN Wei.Statistics analysis of HF broad-beam sea-echo spectra[J].Chinese Journal of Radio Science,2006,21(3):432-436.(in Chinese)