气动脱模用多孔材料的气体流动性能

蒋炳炎，邱庆军，翟瞻宇，申瑞霞

(中南大学 机电工程学院 高性能复杂制造国家重点实验室，湖南 长沙，410083)

微注射成型技术从常规注射成型技术发展而来，与常规注射成型过程一样，包括合模、注射成型、脱模3个阶段[1-2]。脱模作为微注射成型中的一个重要阶段，担负着将微制品与微型腔顺利脱模的任务，因为要克服模具和聚合物之间形成的黏附力、热收缩应力以及摩擦力等作用，所以，脱模过程在很大程度上决定了微制品的最终成型质量，脱模系统设计不当将造成微结构产生犁沟、破裂、表面粘附等现象[3-4]。微注射成型领域通常采用直接推顶制品的方法实现脱模[5-7]，但该方法容易在微制品表面留下疤痕，影响表观质量，且轻微的受力不均都将造成微制品翘曲变形甚至断裂。随着科学技术的进步，微制品的尺寸将更小，为保证制品的成型质量，脱模过程中应使制品受力均匀且平稳地从型腔中脱出。多孔材料的出现为微注射成型制品脱模过程出现的新问题提供了一个新的解决途径。将多孔材料直接加工成镶嵌件作为气动脱模介质，使气体通过其微孔直接到达制品的底部，由于气体的等压性，可确保脱模时制品受到均匀的顶出力，不发生传统脱模机构引起的翘曲变形现象，显著提高制品的成型精度和表观质量。本文选择多孔材料即透气钢作为脱模介质，因此，研究流体在其微孔中的流动规律是构建这种新型气动脱模系统的前提。流体通过多孔材料的流动一般分为分子流和黏性流。黏性流又有层流和紊流之分，其判断参量为雷诺数Re[8]。若流体的雷诺数Re小于临界雷诺数Rec，则流体呈层流状态，服从层流规律；反之则为紊流。渗透率和惯性系数是与多孔材料中的流体流动特性相关的2个十分重要的参数[9-10]，通常有关气体的流动状态测定实验都将通过多孔材料的气体视为不可压缩体，然后直接根据Darcy-Forchheimer定律得出这2个参数[11-12]。这种近似对实验条件如样品厚度、工作压力等提出了很多较为严格的要求：气体只有在低流速和低压力下才可视为不可压缩流体，因此，通常实验都需在低流速和低压力下进行；为了保证渗流速度均匀，样品必须很薄[13]。为此，李亨等[14]提出了在考虑气体压缩性的情况下测定透过系数和惯性系数的方法，该法可大大减少实验时对样品厚度和工作压力等条件的限制。在此，本文作者在考虑气体压缩性的情况下测定透气钢的渗透率和透过系数，揭示不同气体状态下透气钢中气体的流动规律，为其应用于气动脱模系统提供数据支持。

1 雷诺数的计算

由于多孔材料中的孔道结构复杂，雷诺公式的表达形式各异，且均未综合考虑影响雷诺数的所有因素，雷诺数目前只能用实验的方法才能确定。

1.1 摩尔根公式

摩尔根将孔道考虑为圆柱状，其关于过滤材料的雷诺数可用下式表达：

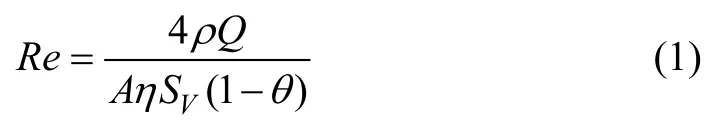
式中：ρ为流体密度；Q为流体流量；A为流体通过的多孔材料截面积；η为流体的黏滞系数(黏度)；SV为多孔材料的体积比表面积；θ为多孔材料的孔率。

1.2 球粒制多孔材料经验公式

对于球形颗粒为原料制备的多孔材料，计算其临界雷诺数Rec的经验公式[8]为：

式中：为多孔材料的平均孔径。此公式对孔隙率为0.35～0.45，平均孔径由2～10 000 μm之间变化的球形粉末制取的多孔材料是适用的。

透气钢为一种粉末烧结多孔材料，根据厂方提供的数据，其平均孔径为 7 μm，代入式(2)得：Rec≡。

2 考虑气体可压缩性的透过性能实验

2.1 测试原理

一维管道中可压缩气体通过多孔介质的定常非Darcy流动分析示意图如图1所示[15]：压力为p1、密度为ρ1、速度为u1的气体通过厚度为δ的多孔介质后，各参量相应地变成p0，ρ0和u0。为建立合适的数学模型，对所分析的流动作如下假设：

(1) 流动定常；

(2) 流动为满足 Darcy-Forchheimer定律的非Darcy流动；

(3) 流体压力足够大，忽略Klinkenberg效应(滑脱效应)；

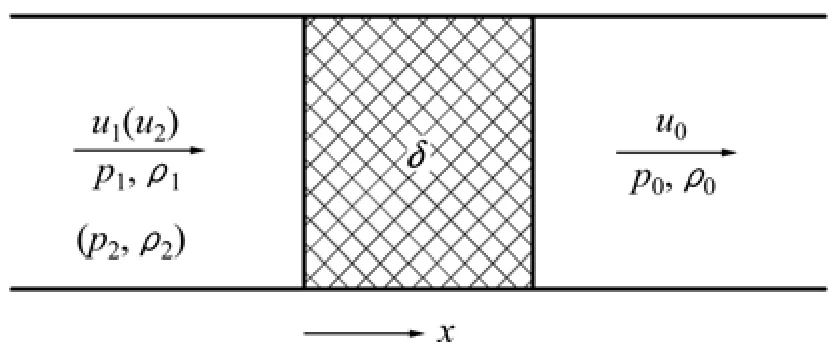
图1 流动示意图Fig.1 Schematic diagram of physical model

(4) 流动为等温流动状态，即流体的温度T和黏性系数η为常量；

(5) 多孔材料为刚性多孔材料，即多孔材料的透过系数B和惯性系数CF均为常量。

通过推演可以得出以下各式：

式中：CF为多孔样品的气流惯性系数；B为多孔样品的气体透过系数；M为气体的摩尔分子质量；R为气体常数；T为气体的热力学温度。若气体通过多孔材料后膨胀为压力为p0和质量密度为ρ0的状态，则可根据 2个工况参数计算出多孔材料的透过系数和惯性系数。

具体实验时可先测出一系列的材料前压力和流速，然后由所有可用的数据对(即两两组合的数据)来计算材料的透过系数和惯性系数(舍弃由实验误差等造成的不合理结果)，再将结果进行平均即得最后的测试结果。

2.2 测试装置

气动脱模用多孔材料测试装置主要由流量计、压力表和透气钢样品室等主要部件组成，气路系统如图2所示。图2中，气源是压力为0.8 MPa的空气压缩机，透气钢样品置于样品室内，气流经样品直接流到大气中。样品室简图如图3所示。

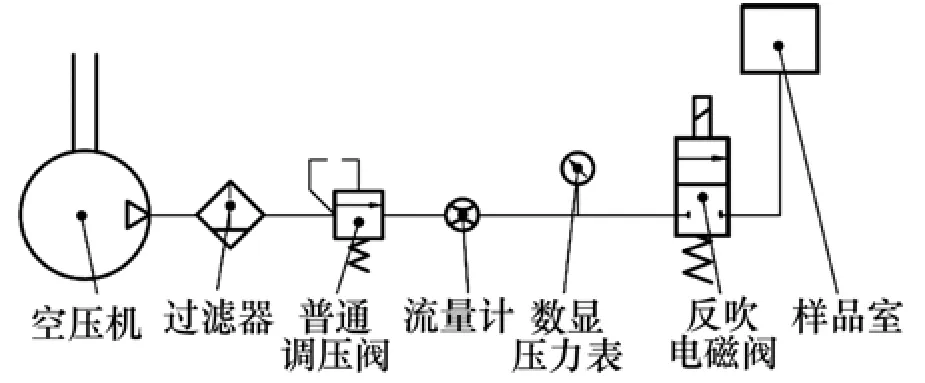
图2 测试气路图Fig.2 Setup of measurement apparatus

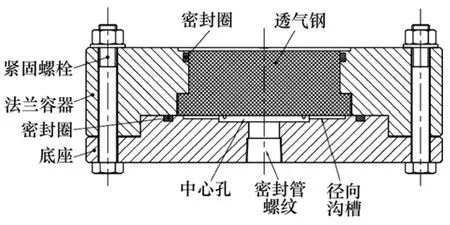
图3 气动脱模用多孔材料样品室Fig.3 Sample cell of porous material for pneumatic demolding

样品室底座上开有螺纹孔，通过密封管螺纹与气路连接，样品室与底座通过螺栓相连，起到固定透气钢样品的作用。气流通过底座下部孔流过样品，再经透气钢流入大气中。进行实验时，压缩空气通过密封管螺纹孔，经过中心孔和径向沟槽均匀地传递到透气钢样品上，并通过透气钢内部的孔隙与大气接通，此时不断地调节调压阀并记录透气钢样品前端压力和流量的对应关系，根据实验数据计算黏性流动系数和惯性流动系数。

3 结果与讨论

透气钢样品的测量结果如表1所示。样品前的气流速度u根据样品前的流量Q和样品的截面积A计算，即u=Q/A；材料前压力根据数显压力表读数换算，并根据式(1)计算对应的雷诺数Re。

为了便于数据分析，将雷诺数随材料前压力的变化绘制成散点图，如图4所示。从图4可以看出：考虑气体可压缩性时透气钢中流体流动分为2个阶段，即当压降为 0.277～0.385 MPa时，Re＜Rec，流体为Darcy流动状态，此时黏性力起主要作用，惯性力可忽略不计；当压降为0.403～0.679 MPa时，Re＞Rec，流动为非 Darcy流动状态，此时惯性力的影响不能忽略。

3.1 Darcy流动状态下透气钢透过系数的计算

在式(3)中，令气体惯性系数 CF=0，Qηδ/A与呈线性关系，其斜率即为透过系数B。将压降在 0.277～0.385 MPa区间的Qηδ/A与的比值导入数据分析绘图软件OriginPro7.5中，得到拟合曲线的斜率即为透过系数B，其值等于4.789 12×10-13m2。将B代入式(3)得到流动方程为：

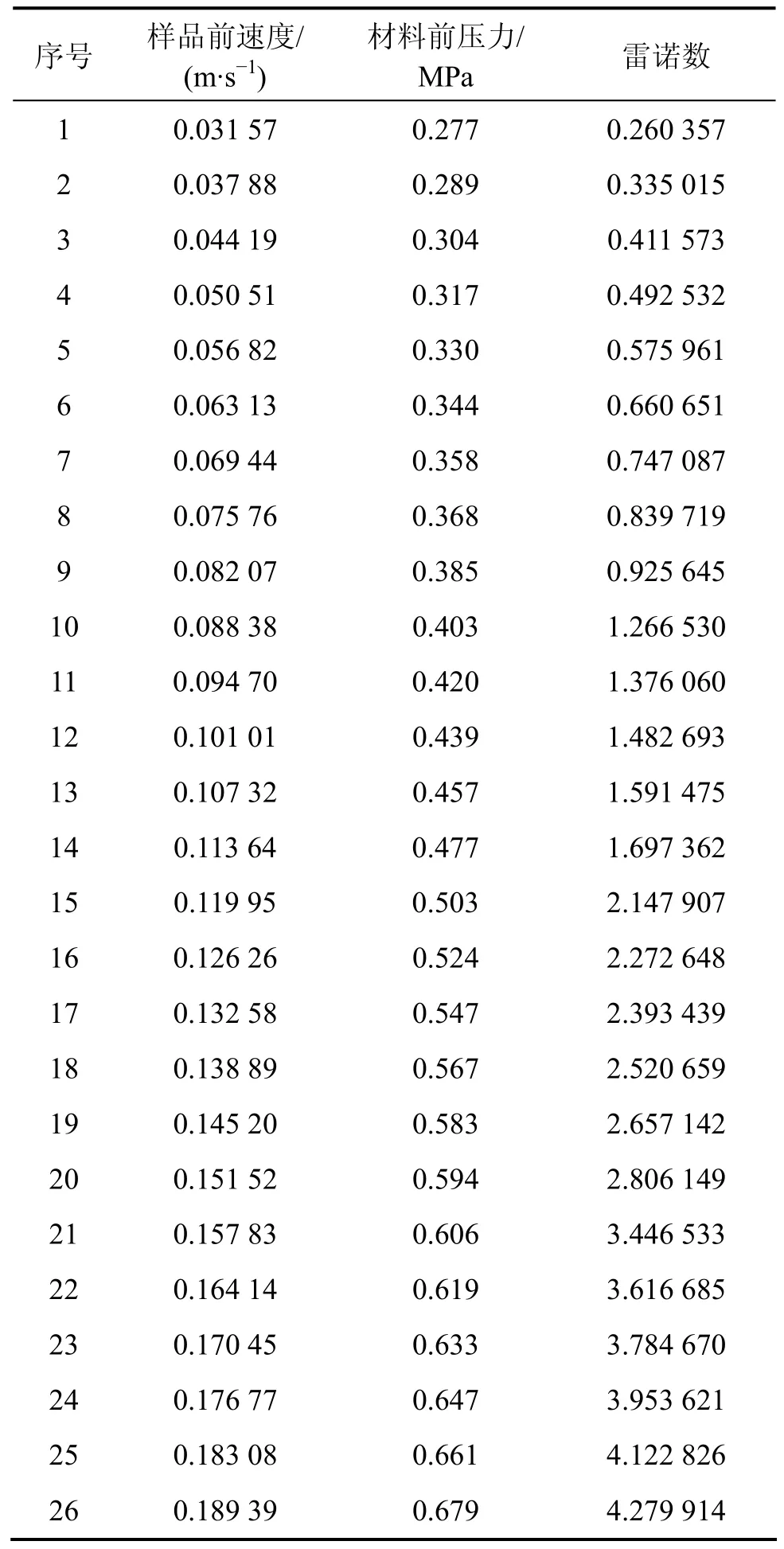
表1 透气钢样品测试结果Table 1 Experimental data of permeable steel

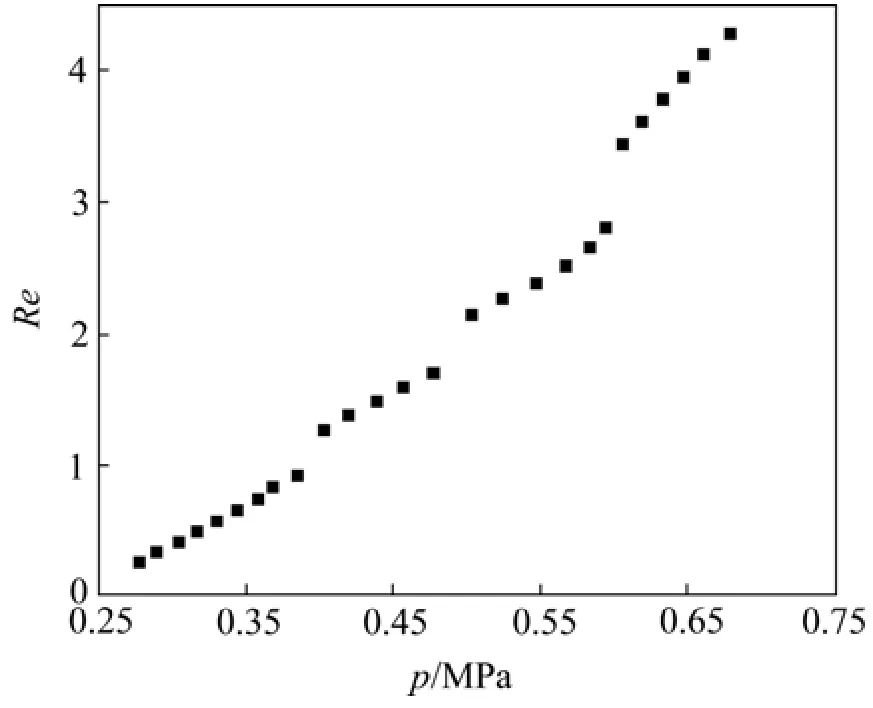
图4 透气钢雷诺数Re随材料前压力p的变化Fig.4 Value of Re as a function of p

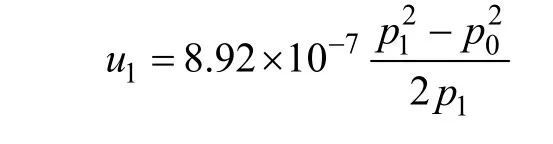
3.2 非 Darcy流动状态下透气钢透过系数与惯性系数的计算

对于压降在0.403～0.679 MPa之间的非Darcy流动，共17组数据。将每一组数据与其他任一组数据联立，根据式(3)～(6)即可得到一组透过系数B和惯性系数CF。由于数据的对称性，在得到的这些系数中只有一半是独立的，所以，一共可以得到136组系数。在这136组系数中，相邻的两组数据由于在压力和流速上相差不大，测量时的读数误差会导致较大的计算误差。为了尽可能减小这种误差，设定实验数据点编号之间的最小间距d，将由间距小于d的数据对联立求得的B和CF除去，将剩余的值平均得到B和CF。当d分别取1，2，4，6和8时，得到的B和CF如表2所示。

表2 透过系数和惯性系数的计算结果Table 2 Calculation results of permeability and inertial coefficient

将所有的B和CF画图，得到B和CF的分布，如图5和图6所示。图中：横坐标N为系数的个数。可以看出：除个别点外，绝大部分数据点计算得到的B和CF都很接近，而且d越大，不合理的数据点越少，计算出的B和CF也越接近。

根据表 2，取B=1.83×10-13m2，CF=-1.87×107s2/m2。将其代入式(3)得到非Darcy流动时的流动方程为：

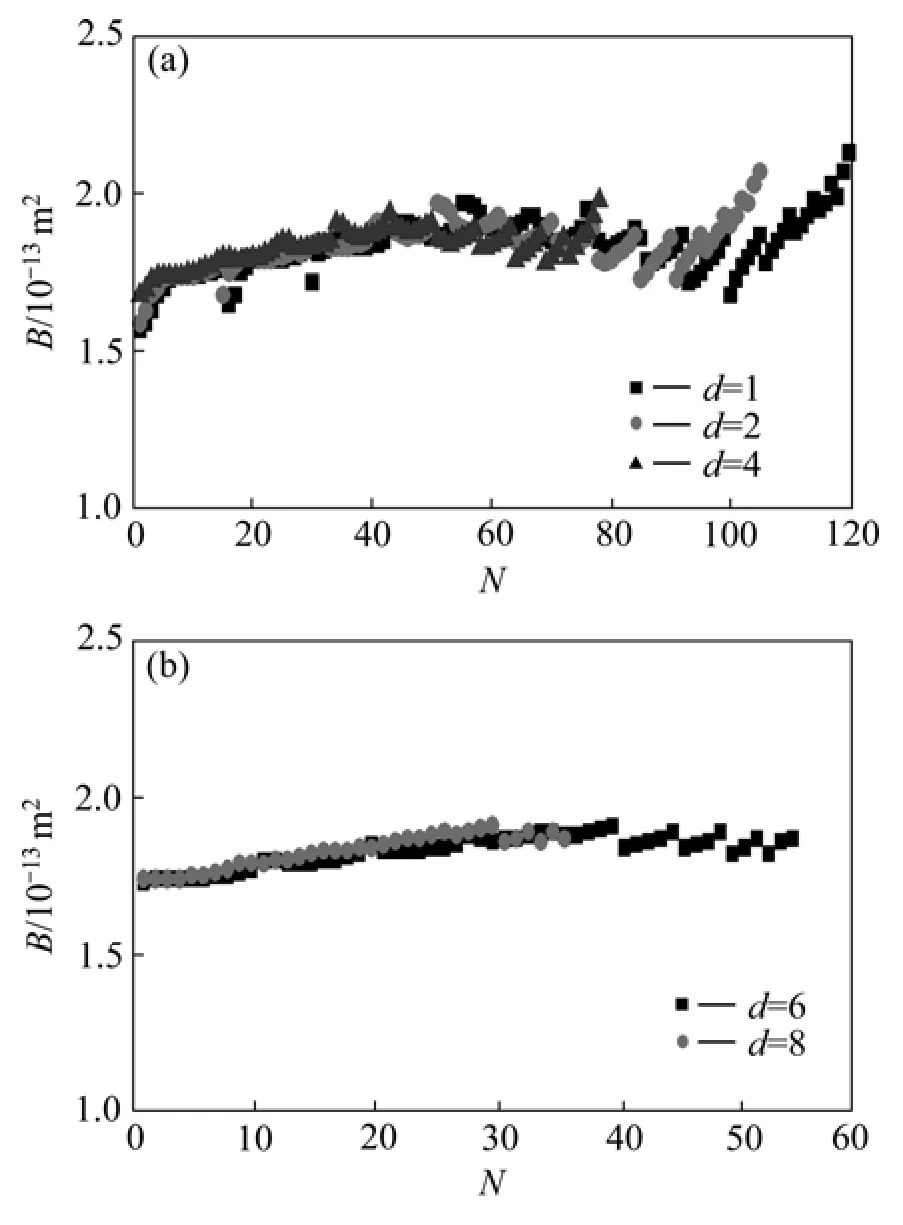
图5 透过系数B的分布Fig.5 Distribution of permeability

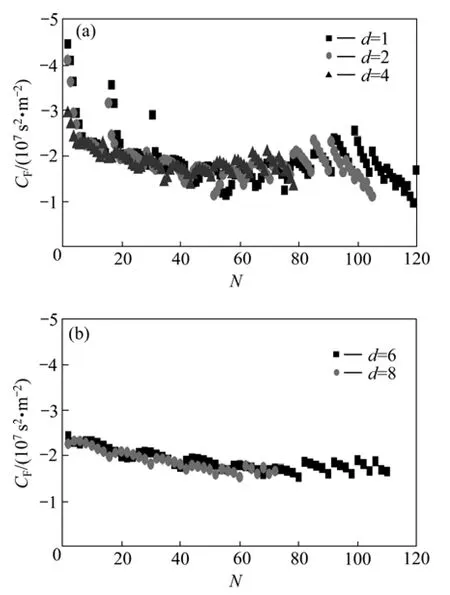
图6 惯性系数CF分布Fig.6 Distribution of inertial coefficient CF

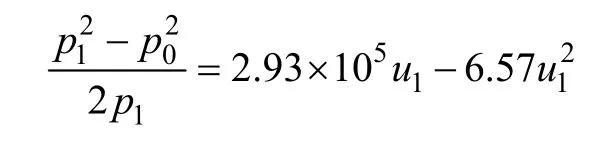
4 结论

(1) 计算出透气钢的临界雷诺数为1.138 72，据此可判断流体通过时流动状态为Darcy流动或非Darcy流动。

(2) 在考虑气体可压缩性条件下，得到了气体通过透气钢时在不同流动状态下透气钢的透过性能参数，推导出对应的流动状态方程，揭示了透气钢中气体不同状态下的流动规律，为深入研究一定气源压力下达到所需脱模力的时间提供了理论基础。

[1] Huang C K. Polymeric nanofeatures of 100 nm using injection moulding for replication[J]. Journal of Micromechanics and Microengineering, 2007, 17(8): 1518-1526.

[2] Pouzada A S, Ferreira E C, Pontes A J. Friction properties of moulding thermoplastics[J]. Polymer Testing, 2006, 25(8):1017-1023.

[3] Bhagavatula N, Michalski D, Lilly B, et al. Modeling and verification of ejection forces in thermoplastic injection moulding[J]. Modeling and Simulation in Materials Science and Engineering, 2004, 12(3): S239-S254.

[4] Bataineh O M, Klamecki B E. Prediction of local part-mold and ejection force in injection molding[J]. Journal of Manufacturing Science and Engineering, 2005, 127(3): 598-604.

[5] Dieudonne A M, Emil G, Albert P P, et al. Injection molded microfluidic chips featuring integrated interconnects[J]. Lab Chip, 2006, 6(10): 1346-1354.

[7] Griffiths C A, Dimov S S, Brousseau E B, et al. Investigation of surface treatment effects in micro-injection moulding[J].International Journal of Advanced Manufacturing Technology,2010, 47(1/2/3/4): 99-110.

[8] 宝鸡有色金属研究所. 粉末冶金多孔材料: 下册[M]. 北京:冶金工业出版社, 1979: 34-35.Baoji Institute for Nonferrous Metal Research. Porous materials powder metallurgy: Last volume[M]. Beijing: Metallurgical Industry Press, 1979: 34-35.

[9] 孙继国, 王建华. 烧结多孔结构的渗透和流阻特性研究[J].航空动力学报, 2008, 23(1): 130-133.SUN Ji-guo, WANG Jian-hua. Research on permeability and flow resistance characteristic of sintered porous structure[J].Journal of Aerospace Power, 2008, 23(1): 130-133.

[10] 李忠全, 周桂芬, 陈木兰. 多孔材料气体渗透性的测定[J]. 粉末冶金技术, 1996, 14(1): 52-57.LI Zhong-quan, ZHOU Gui-fen, CHEN Mu-lan. Determination of gas permeability of porous materials[J]. Powder Metallurgy Technology, 1996, 14(1): 52-57.

[11] 罗民华, 曾令可. 多孔陶瓷的表征与性能测试技术: 下[J]. 佛山陶瓷, 2004, 14(2): 3-6.LUO Min-hua, ZENG Ling-ke. Characterization and testing technology of porous ceramics: Last volume[J]. Foshan Ceramics, 2004, 14(2): 3-6.

[12] Moreiraa E A, Innocentinib M D M, Courya J R. Permeability of ceramic foams to compressible and incompressible flow[J].Journal of the European Ceramic Society, 2004, 24(10/11):3209-3218.

[13] 刘培生, 杨全成, 周茂奇. 多孔材料透过性能的表征[J]. 钛工业进展, 2006, 23(4): 12-16.LIU Pei-sheng, YANG Quan-cheng, ZHOU Mao-qi. Expression of permeation property of porous materials[J]. Titanium Industry Progress, 2006, 23(4): 12-16.

[14] 李亨, 张锡文, 何枫. 考虑气体压缩性的多孔材料渗透率和惯性系数的测定[J]. 实验力学, 2002, 17(3): 326-332.LI Heng, ZHANG Xi-wen, HE Feng. Measurement of permeability and inertial coefficient for porous materials with the consideration of compressible effects of gas[J]. Journal of Experimental Mechanics, 2002, 17(3): 326-332.

[15] 李亨, 张锡文. 可压缩气体定常非 Darcy渗流的流动分析及其应用[J]. 应用力学学报, 2003, 20(1): 1-4.LI Heng, ZHANG Xi-wen. Analysis of non-Darcy steady compressible gas flow In porous media and its application[J].Chinese Journal of Applied Mechanics, 2003, 20(1): 1-4.