外套加层结构中的隔震支座优化参数研究

閤东东， 苗启松， 李文峰

(北京市建筑设计研究院，北京 100045)

在既有建筑上加层，可以增加建筑的使用面积，改善房屋抗震能力，延长了建筑物使用年限。将抗震加固和加层改造结合起来，具有显著的社会和经济效益[1]。外套框架加层法就是常用的结构加固加层方法，分为分离式和整体式两种，分离式加层具有传力路径明确，增加的结构平面布置灵活，不受原结构限制等特点。但分离式外套框架结构易形成“高鸡腿”结构，对抗震很不利，在地震区使用存在一系列亟待解决的技术问题，我国是一个地震频发的国家，其中23个省会城市和2/3的百万人口以上的大城市位于7度以上的地震高烈度区域，因此该课题的研究具有一定的工程应用价值。

原结构和外套结构实际上可看成两个相对独立的结构，在两结构的动力特性显著不同时，采用隔震装置等连接时，可以利用两结构之间的相对运动耗能减震[2，3]。隔震技术靠刚度相对较小的隔震层，使变形主要集中在隔震系统中，起到耗能减震作用，可用于已建成建筑物进行加层加固[4～6]等等。李宏男等对采用层间隔震加固技术进行了试验研究[2，3]，并应用于沈阳市北京路某四层建筑加层加固，在原结构和外部框架之间用软钢阻尼器连接，并在原结构顶层和增加的结构底层设置滑动摩擦层。对于基础隔震结构，我国《建筑抗震规范》给出了隔震支座设计的具体方法，但是隔震装置设置在原结构与外套结构之间时，隔震支座设计需要进行专门研究。比较通用的方法就是通过复杂的参数化研究得到隔震支座的参数，这样需要分析大量的参数样本，总结结构响应随隔震支座参数的变化规律，然后综合考虑结构的响应，得到隔震支座的参数，这对于实际工程结构需要耗费大量的计算时间，并且不具有通用性，针对不同的结构均需要进行参数化研究，不利于这种加固方式的推广。

朱宏平等对相邻结构间弹簧和阻尼器并联的Kelvin型阻尼器优化参数进行了一系列研究，通过大量的公式推导和参数化研究表明阻尼器与相邻两结构的第一阶自振圆频率和总质量有关[7]，并给出了理论表达式，但该优化参数仅适用于在地震作用下，结构处于线性状态的假设。工程应用中，在大震作用下结构也会产生强烈的非线性。因此，隔震支座的参数选取具有相当的难度。

本文采用Bouc-Wen模型描述原结构与外套加层结构的滞回特性，采用线性弹簧和线性阻尼器并联的模型模拟铅芯橡胶支座，对不同地震波和不同加速度峰值下的隔震支座优化参数进行了大量的参数化研究。分析结果表明在不同加速度峰值的地震波激励下，隔震支座的优化刚度系数和阻尼系数分别比较接近，且在一定范围内，隔震支座的刚度取值对其耗能减震效果影响不大，说明隔震技术在分离式外套框架加层结构中的应用具有较大的优势。当结构处于线性状态时，通过Kelvin型线性阻尼器模型的理论表达式可得到隔震支座的优化刚度系数和阻尼系数，将其与参数化研究结果进行比较，表明通过理论表达式得到的结果具有一定的参考价值，可用于分离式外套框架加层结构设计中隔震支座的初步选取。

1 结构计算模型与运动方程

分离式外套框架加层隔震计算模型如图1所示，本文对结构计算模型作以下假定[1]:

(1)结构质量集中在楼层，楼层刚度无穷大，原结构与外套结构都简化成多自由度剪切型模型;

(2)只考虑结构的水平平动，两结构平面对称，忽略扭转效应，只考虑沿结构水平向对称面的地震作用，一般结构体型规则，平面布置对称，可以采用此假定;

(3)不考虑竖向地震作用。

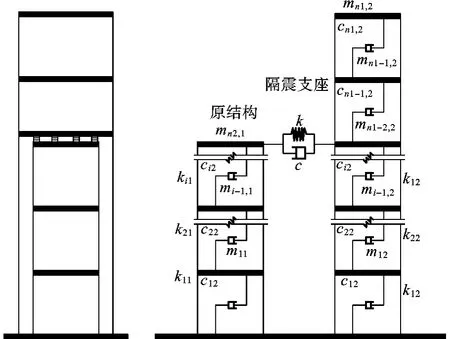
图1 分离式外套框架加层隔震计算模型

原结构和外套结构的层数分别为n1和 n2(n1＜n2)，在地震波激励下，结构体系的运动方程可表示为

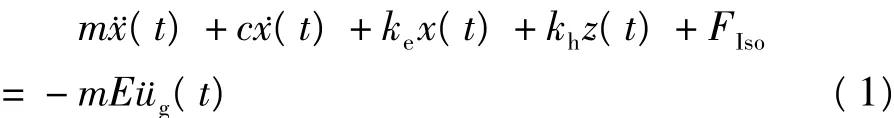
其中，m，ke，kh与 c为结构体系的 n×n(n=n1+n2)维质量、弹性刚度、滞回刚度与阻尼矩阵;x(t)为n维相对地面位移向量;FIso为隔震支座的剪力向量;z(t)为层间滞回位移向量;E为荷载指示向量;g(t)为地面运动加速度。

很多土木工程中的结构在强震作用下表现出滞回特性，Bouc-Wen模型被广泛用于描述各种滞回现象[8]。Bouc-Wen模型通常由一个输出力的表达式与一个一阶非线性微分方程构成，结构i的第j层层间恢复力可表示为

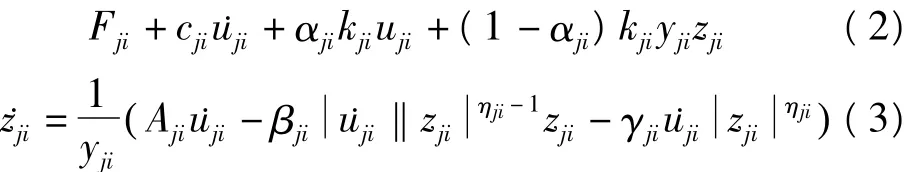
其中，下标i(i=1，2)和j分别代表原结构和外套结构的第j层;αji为屈服系数，表示屈服后刚度与屈服前刚度的比值;yji为层间屈服位移;zji为层间位移滞回分量;uji为层间位移，可表示为uji=xjixj-1，i;Aji，βji，γji控制滞回曲线的形状;ηji决定了从弹性区到塑性区过渡的变化率。

质量矩阵表示为

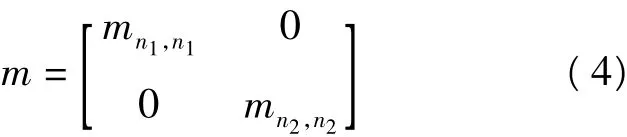
其中

阻尼矩阵表示为

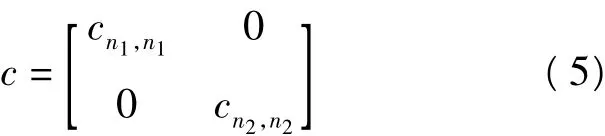
其中

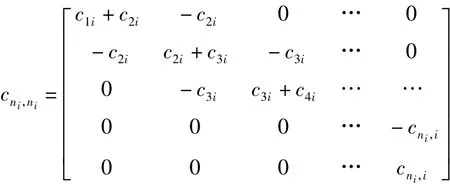
弹性刚度矩阵表示为

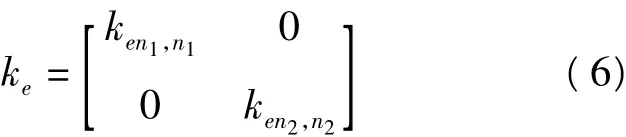
其中

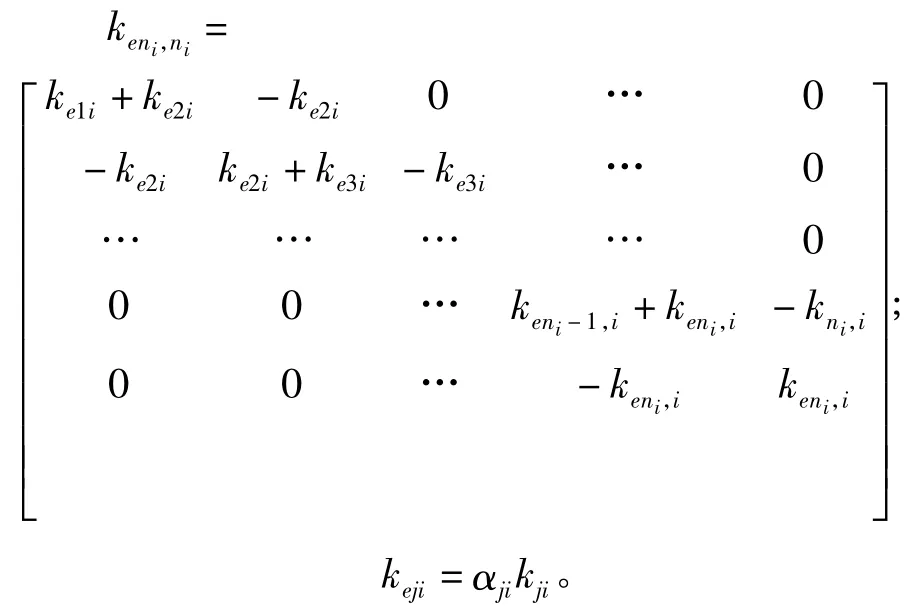
滞回刚度矩阵表示为

2 结构非线性时程分析

在工程应用中，对于高阻尼橡胶支座铅芯叠层橡胶垫可采用弹簧和阻尼器单元并联的Kelvin计算模型[9]。对设置有耗能装置的结构进行初始设计时，也多采用等效线性化模型[10]，因此，本文采用Kelvin型模型模拟隔震支座，恢复力采用下式表示:

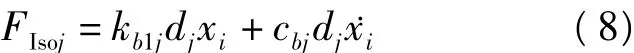
其中，dj为指示向量;djx˙i-1，djxi-1分别表示隔震支座第i-1步的剪切变形速度和位移，djx˙i，djxi分别表示隔震支座第i步的剪切变形速度和位移，均可以由结构速度和位移响应表示。kb1j与cbj分别为隔震支座刚度系数和阻尼系数。

将结构运动方程采用状态空间法表示为微分方程组的形式，表达式如下

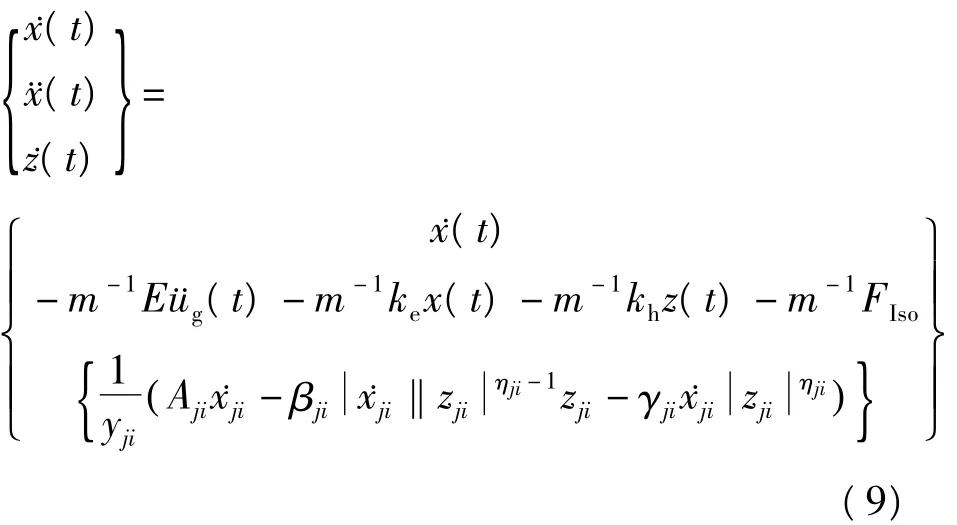
方程(9)是一个一阶微分方程组，描述了一个时变的动力系统。对于这种形式的微分方程组，可以采用四阶龙格库塔法求解。

在地震激励下，经常采用如下的二次型性能指标作为结构振动控制的指标

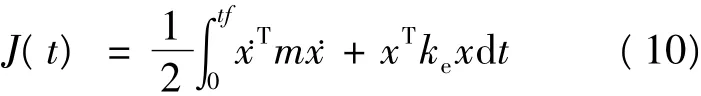
其中，tf为地震波持续时间。实际上，方程(10)代表了相邻结构中的动能。取该指标为控制目标可以保证地震作用下，两结构在各时间步的动能和最小。

3 Kelvin模型优化参数

在(8)式中，当忽略隔震支座刚度退化时，隔震支座的计算模型等效为线性弹簧与线性阻尼器并联的Kelvin模型。Zhu等将地面运动激励简化为白噪声，将相邻结构简化成双体单自由度体系，并推导了采用优化参数[7]。设β=ω2/ω1为外套结构(结构2)与原结构(结构1)的自振频率比，限制结构2与结构1的频率比β≤1，对于β＞1的情形只需将结构1与结构2角色互换即可，μ=m1/m2为结构1与结构2的总质量比。则Kelvin型粘弹性阻尼器总的优化参数βopt与Δopt表达式为

当μ＜1时

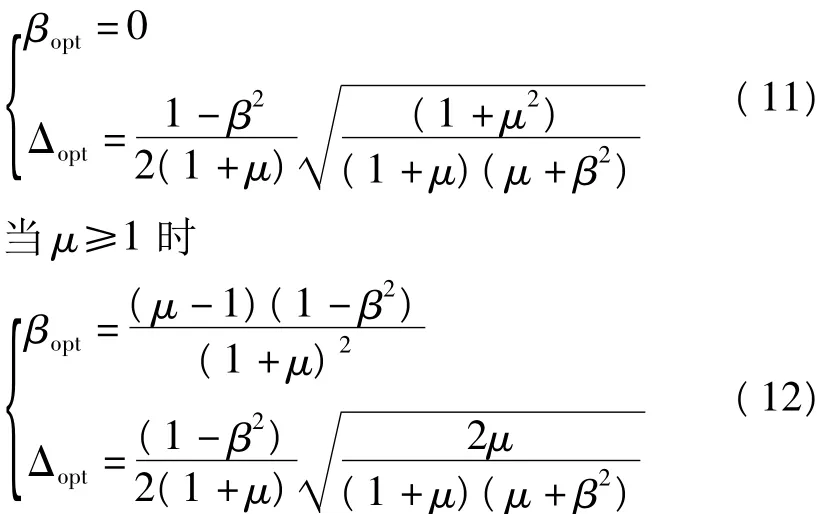
式中，对隔震支座进行初步设计时，忽略结构的非线性特性，则可通过以上表达式得到隔震支座的刚度与阻尼系数表达式如下

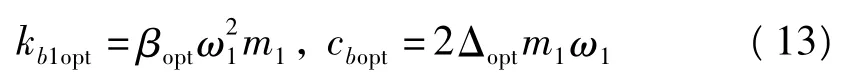
4 工程实例

某机关办公楼为框架结构，共4层，各楼层层高为3.3 m。为改善办公条件，现欲另外增加4层。原结构与外套结构均采用Raleigh阻尼模型，结构第一、二阶振型阻尼比取0.05。原结构与外套结构均采用迟滞剪切型模型建模，假设每层屈服后刚度与屈服前刚度比为0.1，滞回特性控制参数A=1，各层的初始层间刚度K、屈服位移yQ和滞回特性控制参数β和γ如表1所示。地震波选取了El Centro波(NS分量)、Kobe波、Taft波，地震加速度峰值取0.2g和0.4g两种情况。

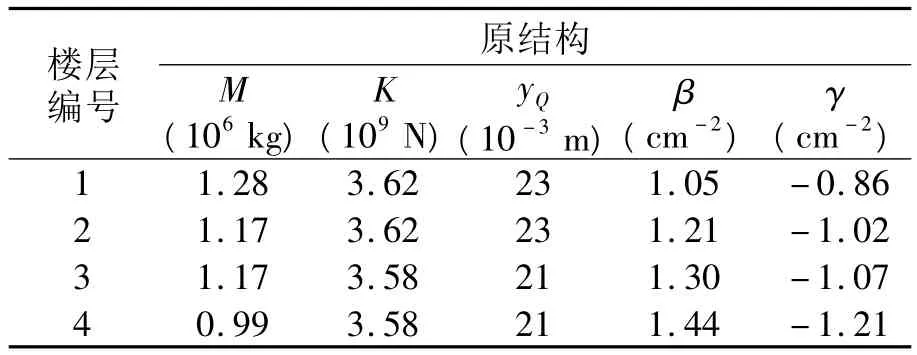
表1 原结构参数

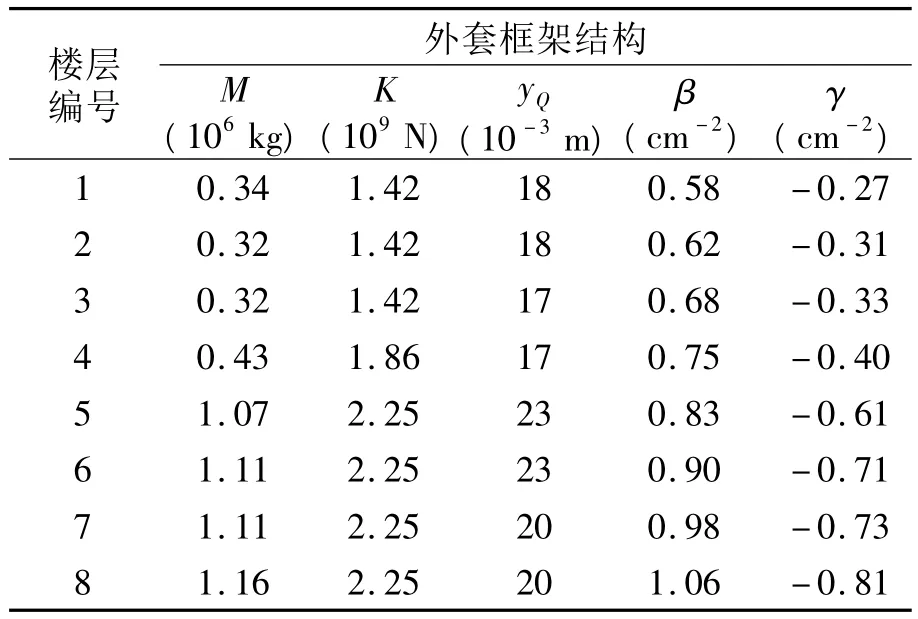
表2 外套结构参数

4.1 隔震支座参数优化

为得到隔震支座的优化刚度和阻尼系数，通常情况下，需要对不同刚度和阻尼系数时的结构样本进行试算，得到不同情况下结构的动力响应，然后对结构响应进行比较，得到隔震支座的优化参数。在此，先通过参数化研究得到结构的响应随隔震支座的参数变化规律。当地震波峰值加速度峰值(PGA)为0.2g时，结构总的振动能量随支座刚度变化规律如图2所示，隔震支座的刚度系数小于1.0×108N/m时，结构响应受刚度影响不大。图3与图4分别给出了原结构和外套结构底层层间位移随支座刚度的变化规律，可以看出kb1小于1.0×108N/m，结构底层层间位移变化不大，但当支座刚度由1.0×108N/m逐渐增大时，则结构响应急剧增大。当PGA=0.4g时，结构总的振动能量随支座刚度系数的变化规律如图6所示，从图中可以发现与PGA=0.2g相同的规律。以上分析结果表明，隔震支座的刚度在某一个范围内时，对结构的响应影响不大，这是隔震支座在这种分离式外套框架加层结构应用的优势。

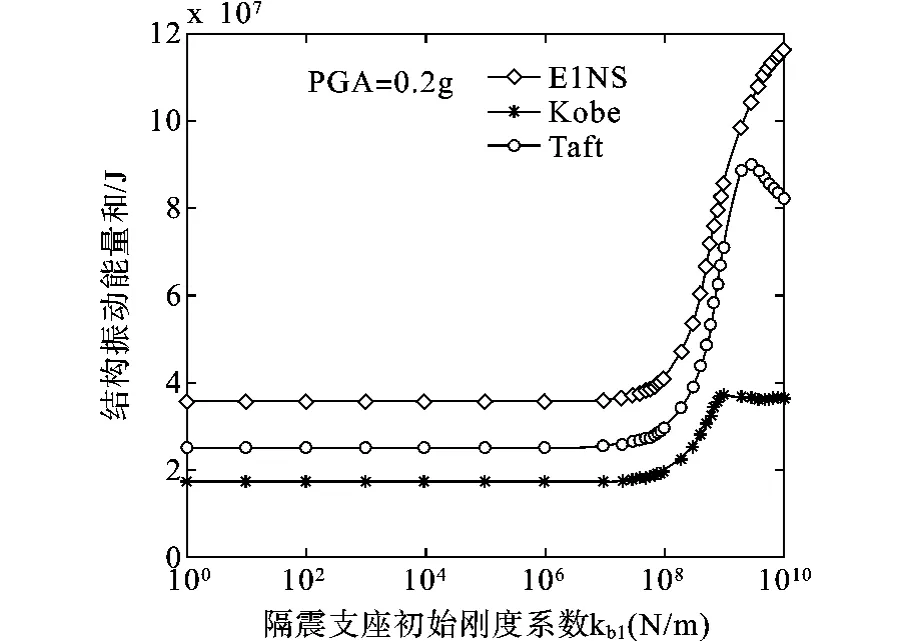
图2 结构动能和随隔震支座刚度变化曲线

图7与图6给出了结构振动能量和随隔震支座阻尼系数cb的变化规律，从图中可以发现，PGA分别由0.2g增大到0.4g时，结构振动能量大大增加，但优化阻尼系数变化不大，约为4.0×107N·s/m。地震波加速度峰值不同并且地震波不同时，隔震支座优化阻尼系数相接近，也为隔震支座在这种分离式外套框架加层结构应用的优势。

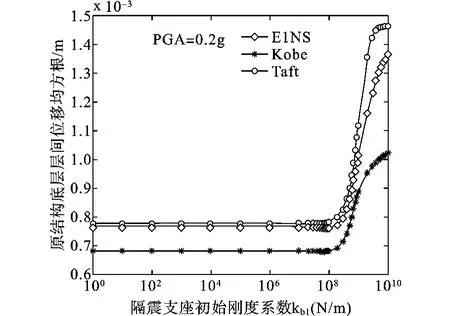
图3 原结构底层位移随隔震支座刚度变化曲线

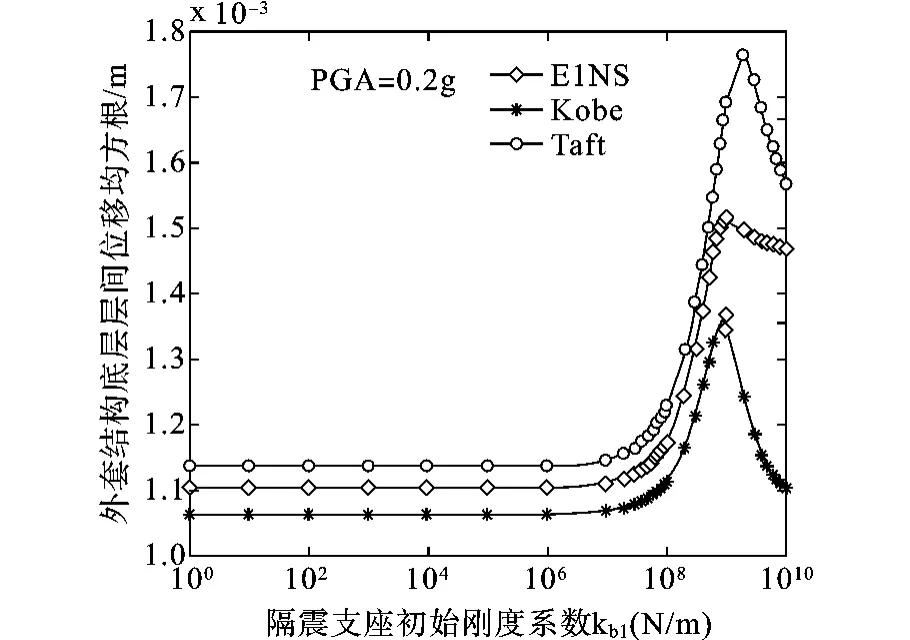
图4 外套结构底层位移随隔震支座刚度变化曲线

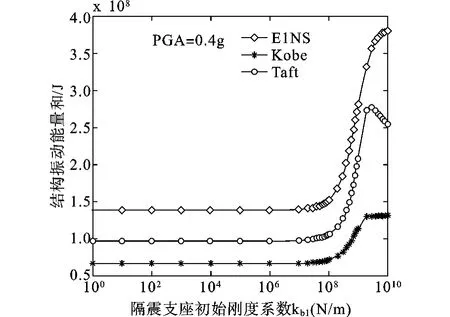
图5 结构振动能量和随隔震支座刚度变化曲线(PGA=0.4g)

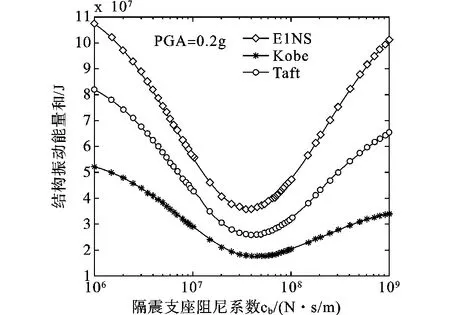
图6 结构振动能量和随隔震支座阻尼系数变化曲线

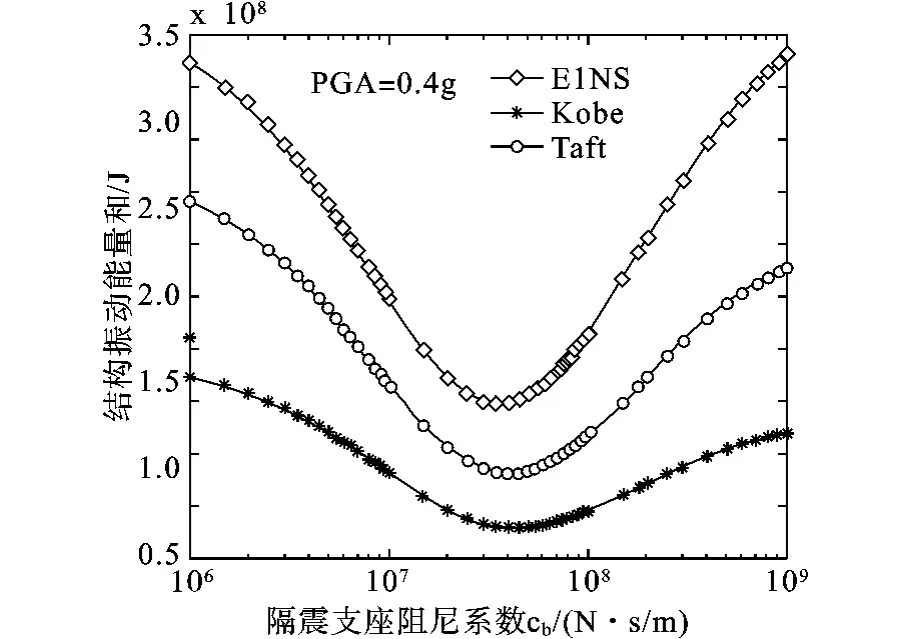
图7 结构振动能量和随隔震支座阻尼系数变化曲线(PGA=0.4g)

当结构为线性状态时，通过特征值分析得到原结构和外套结构的第一阶自振圆频率分别为19.91和7.63 rad/s，总质量分别为4.61×106和5.86×106kg，将结构参数代入理论表达式，得到隔震支座的优化刚度系数和阻尼系数分别为0和4.32×107N·s/m。显然，通过理论表达式得到的阻尼系数优化结果与通过繁琐的参数化研究得到的结果是一致的。当隔震支座刚度取0时，对隔震效果几乎无影响。说明理论表达式所得结果具有一定的参考意义，可用于隔震支座的初步优化设计。但实际工程中，隔震支座具有一定的刚度，本文取隔震支座优化刚度系数为1.0×107N/m，优化阻尼系数为4.32×107N·s/m，进一步分析隔震支座的耗能减震效果。

4.2 隔震支座减震效果分析

在El Centro波激励下，PGA=0.4g时，原结构的底层层间位移比较曲线如图8所示，从图中可以看出原结构的响应稍有减小，外套结构的底层位移响应如图9所示，从图中可以看出隔震后的结构响应得到有效的削弱。图10和11分别给出了原结构和外套结构的动能随时间的变化曲线(前15 s)，可以看出结构总的动能峰值较原结构的峰值大大减小，隔震支座发挥了比较好的减震效果。

表3给出了隔震支座的控制效果，从图中可以发现，结构的控制效果与地震波特性密切相关，外套结构由于较柔，其动力响应大大减小，原结构顶层位移控制效果不甚明显，当PGA=0.4g时，位移略有增加，但增加很少。

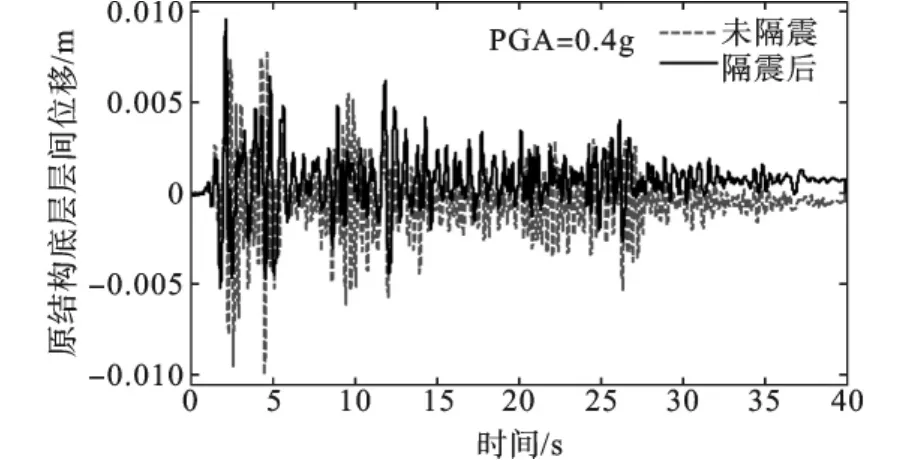
图8 El Centro波作用下原结构底层层间位移时程比较曲线(PGA=0.4g)

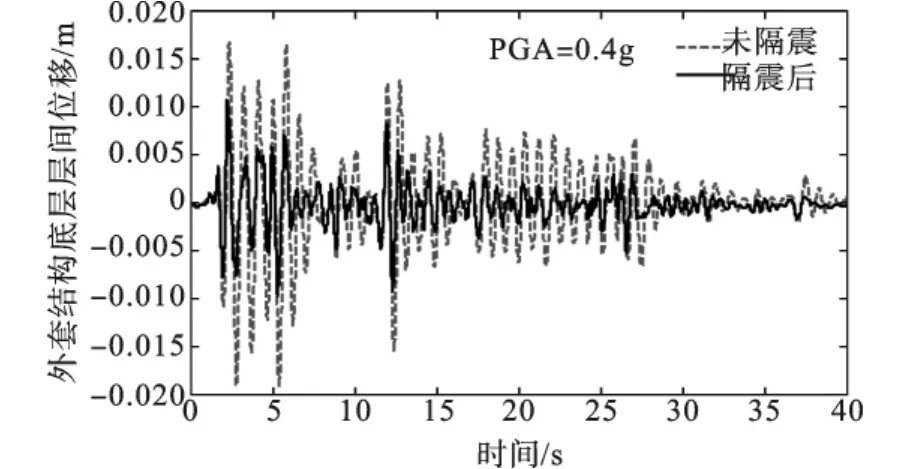
图9 El Centro波作用下外套结构底层层间位移时程曲线(PGA=0.4g)

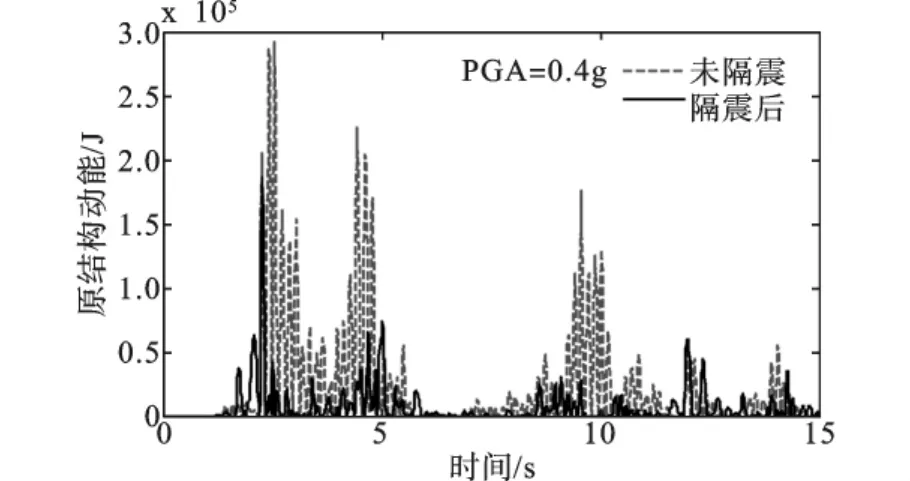
图10 El Centro波作用下原结构动能时程比较曲线(PGA=0.4g)

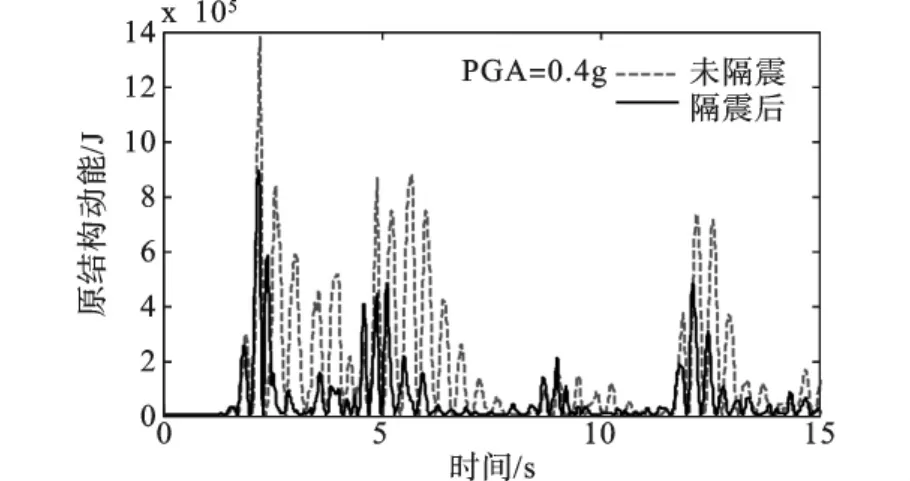
图11 El Centro波作用下外套结构动能时程比较曲线(PGA=0.4g)

以上分析结果说明可基于两单自由度间Kelvin型耗能装置的优化参数表达式得到隔震支座的优化阻尼系数，该表达式可为工程师设计外套结构加层隔震加固体系提供一定的参考，为该类工程的应用奠定了较好的基础。隔震支座的刚度在一定范围内对其消能效果影响很小，是其在外套结构加层隔震加固体系中的应用的另一个优势。

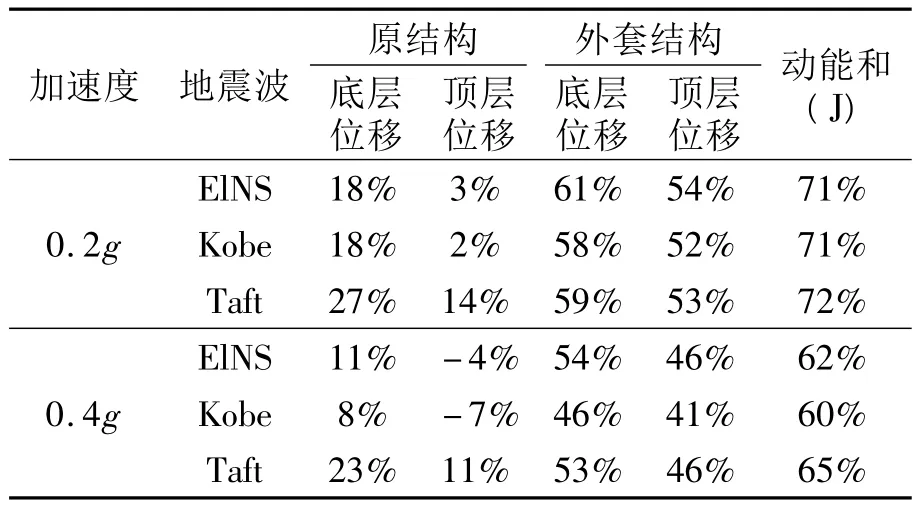
表3 结构在各种地震波作用下耗能减震效果(均方根减小百分比)

5 结论

(1)隔震支座的阻尼系数在不同地震波、不同地震加速度峰值时的优化结果相近，与原结构和外套框架结构的第一阶自振圆频率和总质量有关，且可以基于理论表达式求得。

(2)隔震支座的刚度在一定范围内对其耗能减震效果影响不大，利于隔震技术在这种结构体系中的推广。

(3)隔震支座具有良好的耗能减震效果，“高鸡腿”的外套结构地震响应大大减小，且对原结构的地震响应有一定的削弱。

[1]高剑平.砖砌体房屋外套结构加层改造技术[M].成都:西南交通大学出版社，2010.

[2]Li H N，Wanga S Y，Song G B，et al.Reduction of seismic forces on existing buildings with newly constructed additional studies including friction layer and dampers[J].Journal of Sound and Vibration，2004，269(3-5):653-667.

[3]李宏男，殷永炜，林立岩.采用摩擦和消能装置的加层结构振动台试验研究[J].建筑结构学报，2001，22(4):67-71.

[4]周福霖，张 颖，谭 平.层间隔震体系的理论研究[J].土木工程学报，2009，42(8):1-8.

[5]祁 皑，林云腾，郑国琛.层间隔震结构工作机理研究[J].地震工程与工程振动，2006，26(4):239-243.

[6]Yasuhiro Tsuneki，Shingo Torii，Katsuhide Murakami，et al.Middle-story isolated structural system of highrise building[J].Journal of Disaster Research，2009，4(3):229-238.

[7]Zhu Hongping，Ge Dongdong，Huang Xiao.Optimum connecting dampers to reduce the seismic responses of parallel structures[J].Journal of Sound and Vibration，2011，330(9):1931-1949.

[8]Wen Y K.Method for random vibration of hysteretic systems[J].Journal of the Engineering Mechanics Division，1976，102(EM2):249-263.

[9]Providakis C P.Effect of LRB isolators and supplemental viscous dampers on seismic isolated buildings under near-fault excitations[J].Engineering Structures，2008，30(5):1187-1198.

[10]Hwang Jenn-Shin，Tseng Yi-Shane.Design formulations for supplemental viscous dampers to highway bridges[J].Earthquake Engineering and Structure Dynamics，2005，34(13):1627-1642.