两自由度体系地震碰撞影响因素及防撞研究

龙晓鸿， 李建军， 李 俊， 杨 斌

(华中科技大学 a.土木工程与力学学院;b.华中科技大学控制结构湖北省重点实验室，湖北 武汉 430074)

近年来世界发生的地震灾害都造成桥梁的严重破坏，对整个城市的交通、经济都产生了很大的影响。根据国内外地震研究者的震害调查分析，桥梁梁间碰撞是桥梁震害的重要方面，碰撞对桥梁结构有很大的影响。要研究桥梁的梁间碰撞问题，必须先对桥梁碰撞影响因素有清晰的认识，在此基础上才能提出有效可行的防止碰撞的措施。

Westermo[1]研究了在强烈地震作用下，相邻桥梁自己的结构动力特征、地震波的空间变化以及行波效应的不同对桥梁结构动力响应的影响，研究结果表明这些因素都能引起较大的梁体位移，从而导致桥梁伸缩缝处发生碰撞。Malhort[2]等使用一个简单的两自由度集中质量模型，确定了合理的恢复系数，对一座桥梁进行了详细的碰撞响应分析。在国内，一些学者对桥梁的碰撞问题也进行了相关的研究。李建中[3]针对连续梁桥在地震作用下的碰撞响应进行了深入的研究，建立了考虑支座非线性和桥墩弹塑性的合理的碰撞模型。李忠献等[4]在随机振动理论的基础上，建立了桥梁地震碰撞的临界间隙算法，并用人工地震波的非线性时程分析验证了算法的正确性。国内外学者对碰撞的分析集中在考虑相邻桥梁间隙、相邻桥梁质量比等参数对于桥梁碰撞响应的影响，只是考虑了有限的这几个方面，没有全面的去考虑影响桥梁碰撞的周期比、地震动特征周期和桥梁延性等因素，这些因素对桥梁碰撞响应的影响也是很大的，需要去做全面深入的研究。

为了减小碰撞对结构的影响，很多学者对防止碰撞或者减小碰撞响应的措施进行了研究。其中研究较多的就是粘滞性阻尼器。Stefano Berton等[5]人研究了在相邻联桥梁之间安装粘滞性阻尼器对桥梁结构动力响应的影响，结果得出粘滞性阻尼器可以提高桥梁的整体动力性能，降低发生碰撞的可能性。Kim等[6]研究了一个非线性粘滞性阻尼器防止碰撞的效果，结果表明非线性粘滞性阻尼器可以有效的减小上部结构的相对位移和碰撞力。李忠献等[7]研究了粘滞性阻尼器应用在减小城市桥梁地震碰撞反应的效果，并且提出了阻尼器参数设计的方法，最后用人工波进行时程分析，得出的结果验证了参数设计方法的可行性。李建中等[8]研究了任意荷载作用液体粘滞性阻尼器在桥梁结构抗震中的作用效果。

桥梁梁间碰撞属于接触问题，其影响因素众多，为了更好地描述桥梁的碰撞行为，本文以连续梁桥的两自由度体系简化力学模型为对象，通过方程的标准化，确定影响桥梁碰撞响应的主要因素，在此基础上研究地震作用下的碰撞影响规律;并选取粘滞阻尼器来进行防撞措施研究。

1 力学模型建立及求解

为了更好地了解桥梁结构在遭受地震作用下的碰撞响应，要兼顾解决方法的效率和计算结果的精确性。解析模型的症结是当描述桥梁的所有行为特性时只着眼于碰撞现象。连续梁桥每联桥梁的简化图如图1所示，它可用一种简单的解析模型来进行描述，如图2所示。

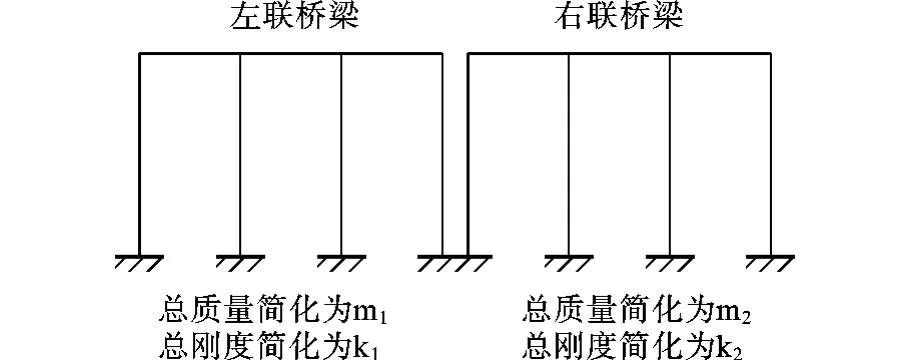
图1 左右两联桥简化图

目前有关桥梁碰撞几种常用的模型有，线性弹簧模型、Hertz模型、Hertz-damp模型、Kelvin模型、改进Kelvin模型和三维接触-摩擦模型，还有基于直杆共轴碰撞理论得出的直杆碰撞模型。由于Kelvin模型采用的是线性弹簧，计算出的位移响应和Hertz-damp碰撞模型基本相似，且Kelvin碰撞模型使用起来比较简单，参数的确定相对简单，并且容易在有限元软件中得到应用。Kelvin碰撞模型如图3所示。

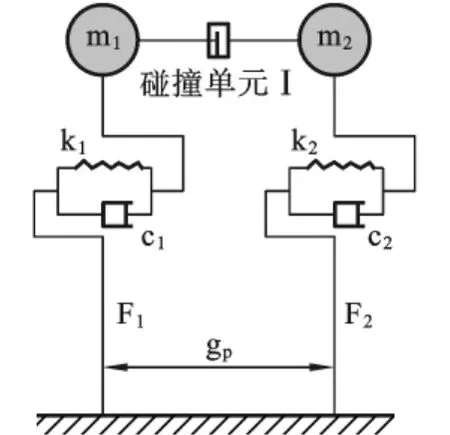
图2 两自由度简化模型

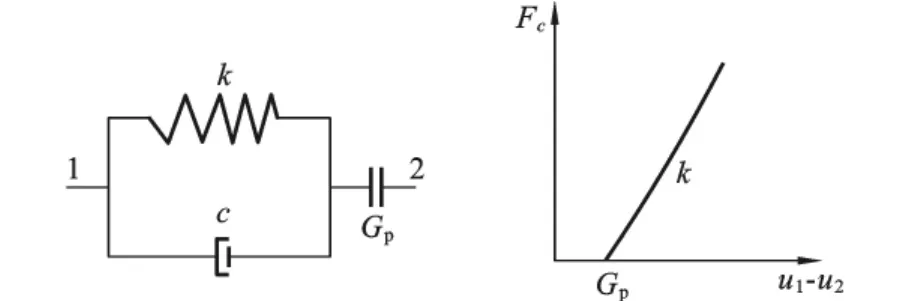
图3 Kelvin碰撞模型及碰撞力-位移模型

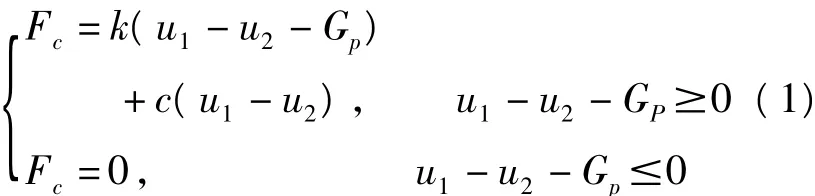
根据能量守恒定律，可以求得阻尼系数c:

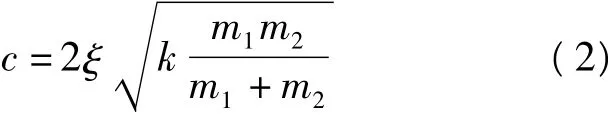
其中ξ是与恢复系数e相关的函数，其表达式为:

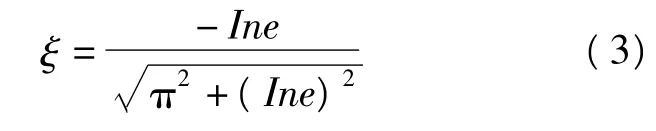
地震作用下两自由度体系的运动方程为

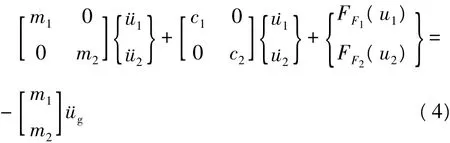
其中，mi是质点质量，ci是体系的阻尼系数，FFi是体系的恢复力，g是地震动加速度。

方程(4)可以用时间控制的逐步迭代算法计算来实现。Newmark法、Wilson-Theta法和Runge-Kutta法是三种常用的算法。由于Runge-Kutta法不需要特定的开始程序，对存储要求比较低，并且能够重复的应用相同的计算方法进行计算;并且数字表达上是稳定的，并且能够比较容易的延伸应用到高阶微分方程中。因此本文中就应用经典四阶Runge-Kutta法，并进行MATLAB编程求解。

2 碰撞影响因素分析

2.1 方程标准化确定碰撞影响因素

为了确定影响两相邻桥梁碰撞响应的主要因素，可将方程进行标准化，其中，定义桥梁的屈服位移为uyi=FFyi/Ki，把方程除以各自的屈服位移可得。其中μi=ui/uyi是桥梁位移延性系数。并把方程除以m2，方程可以变为

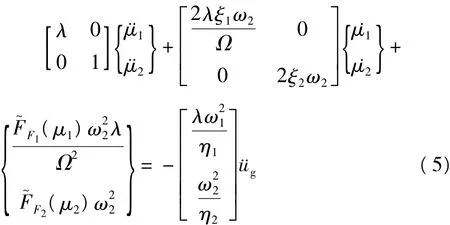
其中，质量比 λ =m1/m2，频率比 Ω = ω2/ω1，标准化的力-位移关系强度比标准化的地震加速度

基于上述方程的标准化，影响桥梁碰撞响应的主要因素可以确定为:质量比λ，桥梁相邻联周期比T1/T2或者刚度比K1/K2，地震动特征周期比T1/Tg和体系延性系数比μ。

2.2 体系碰撞影响因素分析

依据已经确定了影响桥梁碰撞响应的主要因素，在两个自由度体系的简化模型中，表1列出了计算中用到的各个因素的取值。

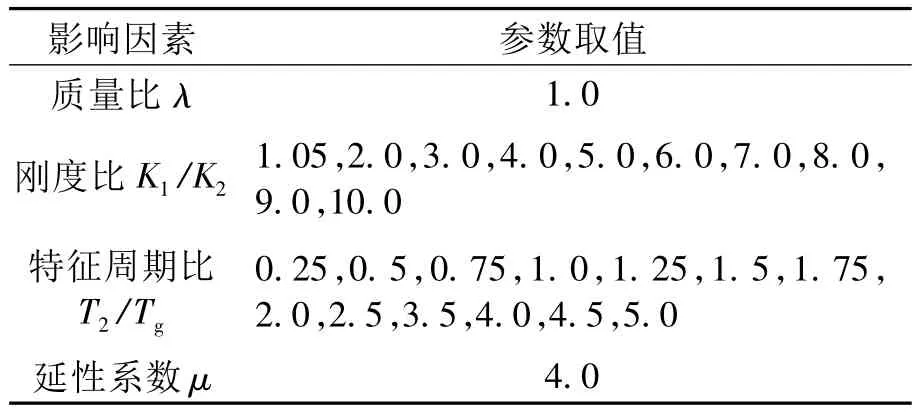
表1 碰撞影响因素计算取值

输入地震动的特征周期和地震加速度峰值范围比较广，并且选取的地震波基本都是6级以上地震的。碰撞响应可以用位移比即位移增大系数γ来表示，位移增大系数γ是发生碰撞时的最大位移与不发生碰撞时的最大位移的比值。

很多结构在遭受强烈地震作用时都会进入非线性工作阶段。为了更好的描述体系屈服后的周期比，采用了有效刚度Keff的概念，有效刚度Keff=K/μ。则体系的有效周期可以表示为

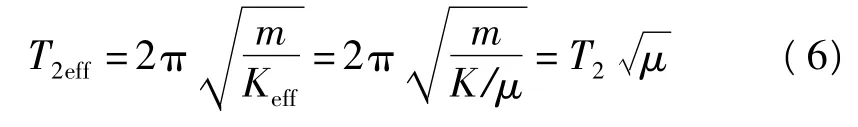
其中T2为右质点在线弹性范围内的周期。为了与线弹性工作阶段相比较，取延性系数μ=4。

考虑体系屈服后的影响，在地震作用下它们的位移增大系数曲线和延性系数曲线如图4，图5所示。

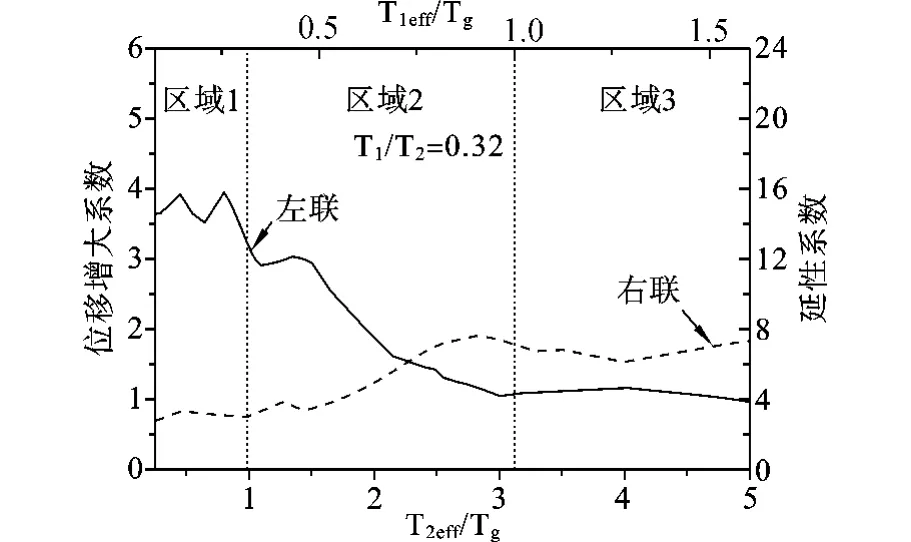
图4 弹塑性结构位移增大系数和延性系数变化曲线(T1/T2=0.32)

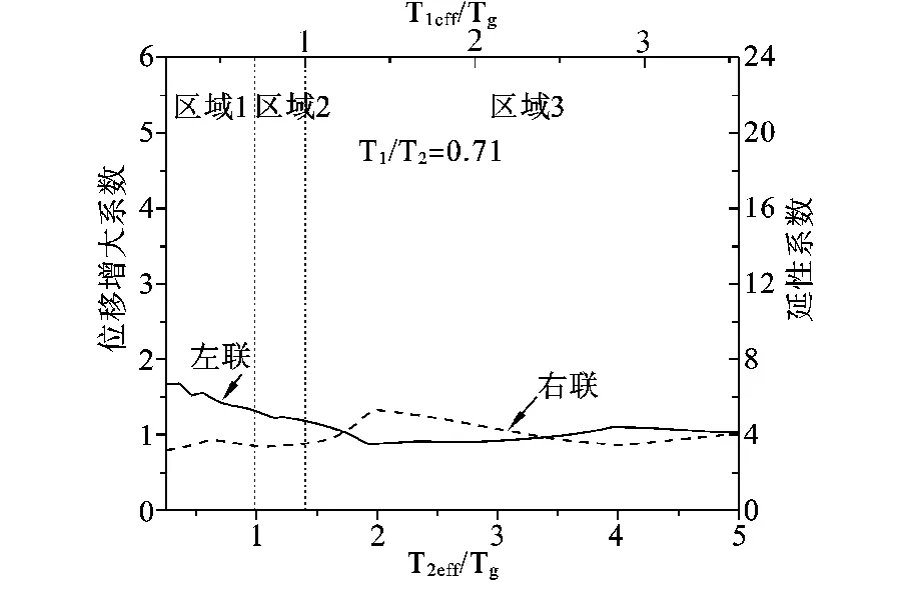
图5 弹塑性结构位移增大系数和延性系数变化曲线(T1/T2=0.72)

区域1是指有效地震动周期比T2eff/Tg≤1的区域。当T1/T2=0.32时，左联体系的延性系数增大了将近3倍，而右联体系的延性系数减小了大约30% 。左联体系的位移增大系数最大为3.9，碰撞的发生使位移增大了290%;右联体系的位移增大系数最小为0.7，碰撞的发生使位移减小了30% 。同线弹性结构比较，当结构考虑了屈服后的影响时，碰撞造成的动力响应要比线弹性结构要大些。

区域2是指周期比T1eff/Tg＜1＜T2eff/Tg的区域。从位移增大系数可以看出，区域2中比起弹性阶段的研究位移增大系数和延性系数都有所增大。区域3是指有效周期比T1eff/Tg＞1的区域，对比弹性阶段的研究可以得出，考虑塑性和不考虑塑性对这一阶段的影响不是很大。但是，考虑塑性之后右联体系的动力响应要比只考虑弹性时的动力响应要小一些，这是屈服之后塑性耗能的结果。相对于弹性阶段来说，考虑塑性之后，结构屈服之后在碰撞产生前结构有一定的相对速度，这个速度的存在使得碰撞响应减小了。塑性阶段结构的响应滞后导致了很大的能量的损耗，这也影响了碰撞响应。同弹性阶段一样，当T1/T2=0.71时，碰撞的发生对结构的动力响应影响很小。

3 粘滞性阻尼器防撞研究

粘滞性阻尼器应用在土木工程领域只有十几年的时间。相对于其他的消能减震装置，粘滞性阻尼器有自己明显的优点:粘滞性阻尼器内置液体，本身没有刚度，这就不会影响到整个结构的周期和原来的设计;粘滞性阻尼器在微小变形下，速度非常小，产生的阻力接近于零，阻尼器不会影响到桥梁结构的正常使用;并且粘滞性阻尼器可以在地震和大风荷载作用下重复使用。

粘滞性阻尼器产生的阻尼力如下式所示

其中，F为粘滞性阻尼器阻尼力，C为阻尼器的阻尼系数，V为阻尼器的拉压速度，α为速度指数。

粘滞性阻尼器的阻尼力-速度关系曲线如图6，阻尼力-位移关系曲线如图7。当α=1时称为线性粘滞性阻尼器，α＜1时称为非线性粘滞阻尼器，速度较小时阻尼器就有较大的阻尼力，而当速度较大时，阻尼力变得增加缓慢;α＞1时称为锁阻尼，速度较小时，阻尼力也非常小，而当速度较大时，阻尼力变得增加很快。

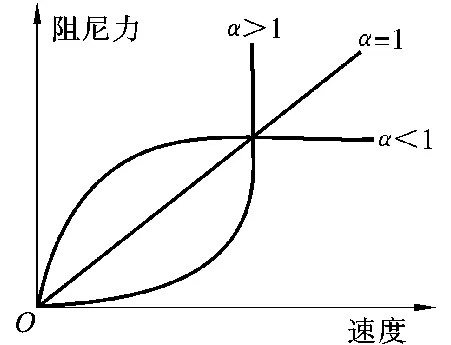
图6 力-速度关系曲线

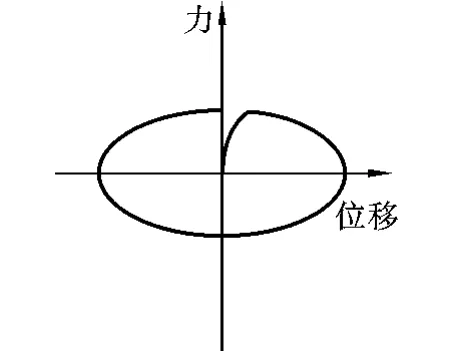
图7 力-位移关系曲线

目前的研究得出，粘滞性阻尼器的速度指数α取值为0.3～1.0。

仍以上述两个自由度为研究对象，在相邻间安装粘滞性阻尼器之后，则体系的的动力响应方程可变为

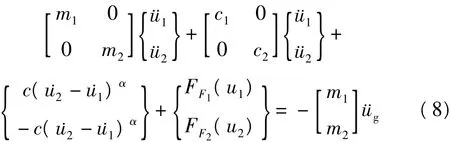
将原方程简化为

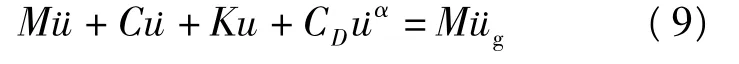
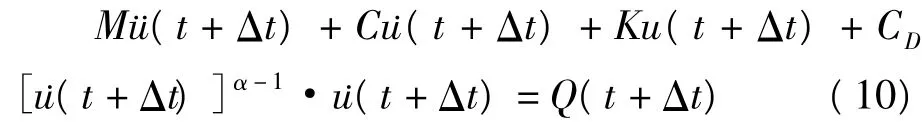
方程的求解步骤如下

(1)设阻尼恢复力为:

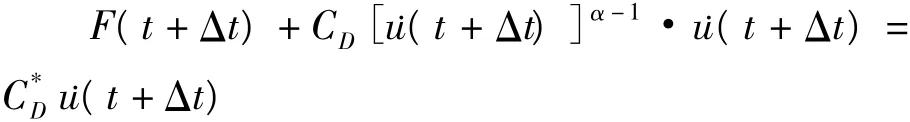
为了计算方便，本文取速度指数α=1。初步选粘滞性阻尼器的阻尼参数c=1×105N·s/m，计算结果如图8～图11。

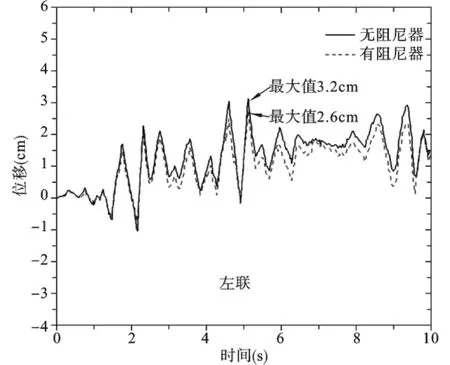
图8 质点m1的位移时程(不碰撞)

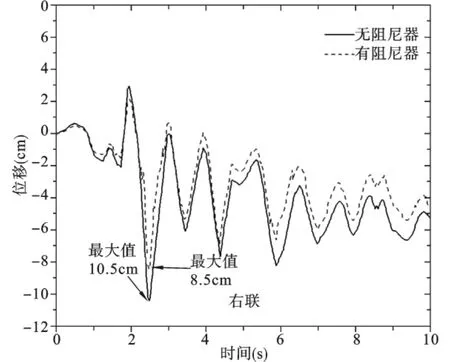
图9 质点m2位移时程(不碰撞)

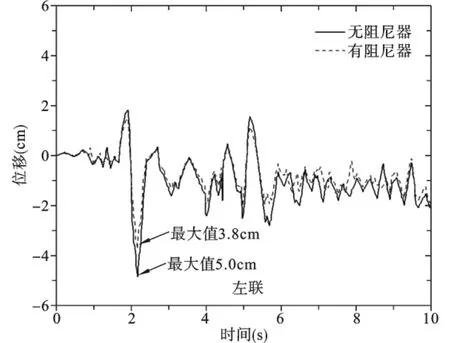
图10 质点m1位移时程(碰撞)

从图8～图11中可以看出，当在两自由度体系之间安装粘滞性阻尼器，两质点的位移响应都有减小，最大减小幅度可以达到25%。从图12可以看出，安装粘滞性阻尼器之后，体系发生碰撞时，碰撞力有所减小，由此可以看出安装粘滞性阻尼器能够有效地减小体系的碰撞响应。

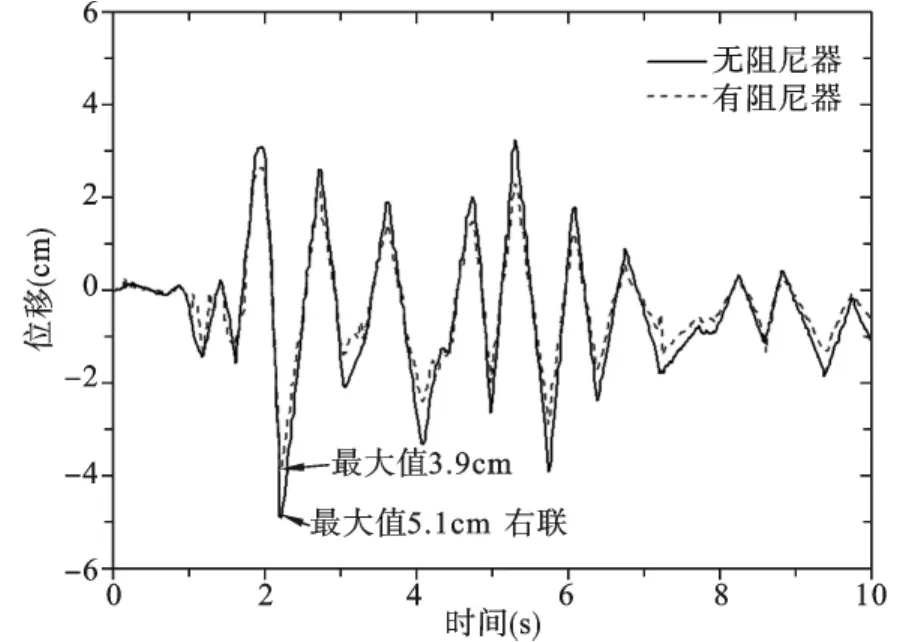
图11 质点m2位移时程(碰撞)

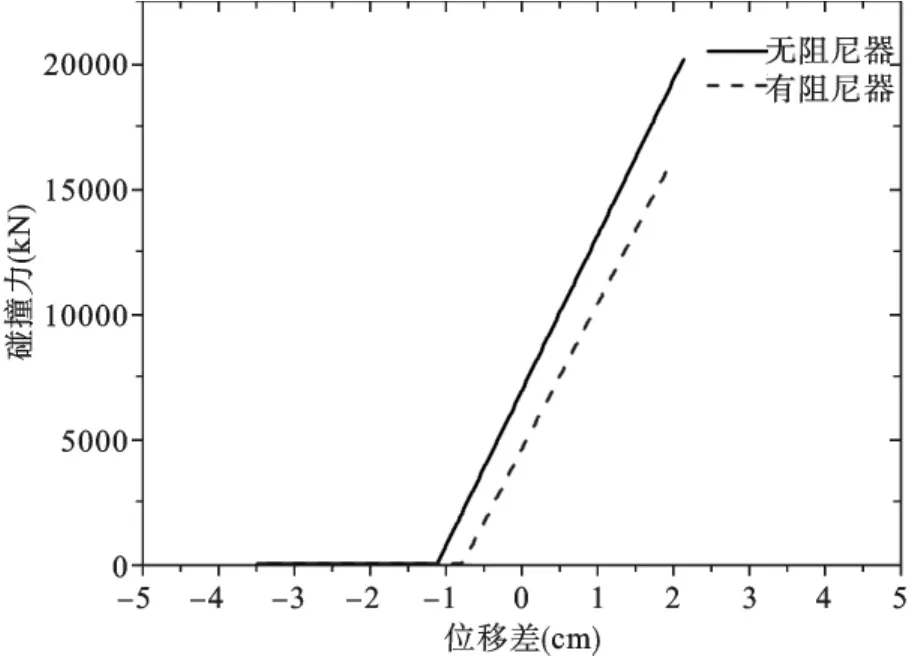
图12 碰撞力对比

4 结论

(1)通过将体系运动方程的标准化，确定影响了体系碰撞响应的主要因素:质量比λ，相邻联周期比T1/T2(刚度比K1/K2)，地震动特征周期比T2/Tg和体系延性系数比μ。

(2)位移增大系数γ的曲线可以分为三个区域，区域1中，碰撞的发生使得质点m1的位移增大，使得质点m2的位移减小。区域3中，碰撞的发生使得m1的位移减小，而质点m2的位移增大。区域2中，碰撞的发生都使得质点位移有一定程度的增大。

(3)当在两自由度体系之间安装粘滞性阻尼器，两质点的位移响应均有所减小，同时体系的碰撞力也减小了，这表明安装粘滞性阻尼器能够有效地减小体系的碰撞响应。

[1]Westermo B D.The dynamic of inter structural connection to prevent pounding[J].Earth quake Engineering and Structural Dynamic，1989，18:687-699.

[2]Malbotra P K，Huang M J，Shakal A F.Seismic interaction at separation joints of an instrumented concrete bridge[J].Earthquake Engineering and Structural Dynamic，1995，24(8):1055-1067.

[3]王军文，李建中，范立础.连续梁桥纵向地震碰撞反应参数研究[J].中国公路学报，2005，18(4):42-47.

[4]李忠献，岳福青.城市桥梁地震碰撞反应研究与发展[J].地震工程与工程振动，2005，25(4):91-99.

[5]Stefano Berton，Hans Strandgaard，Bolander J E.Effects of non-linear fluid viscous dampers on the size of expansion joints of multi-span perstressed concrete segmental box-girders bridge[C]∥proc.of 13th world conference on earthquake.Vancouver ，Canada，2004.

[6]Kim J M ，Feng M Q ，Shinozuka M.Energy dissipating restrainers for highway bridge[J].Journal of Soil Dynamics and Earthquake Engineering，2000，19(1):65-69.

[7]李忠献，周 莉，岳福清.城市桥梁粘滞阻尼器防地震碰撞分析与参数设计[J].地震工程与工程振动，2006，26(5):95-101.

[8]聂利英，李建中，范立础.任意荷载作用下液体粘滞阻尼器在桥梁工程中减震作用探讨[J].计算力学学报，2007，24(2):197-202.