医学CT图像恒模盲均衡算法性能分析
2011-08-01孙云山张立毅段继忠
孙云山 ,张立毅 ,段继忠
(1. 天津大学电子信息工程学院,天津 300072;2. 天津商业大学信息工程学院,天津 300134)
盲均衡算法是一种不需要训练序列,仅利用接收信号本身的先验信息对信道特性进行补偿,使其输出序列尽量逼近发送序列的新兴自适应均衡技术.最早由日本学者 Sato[1]提出并应用于数字通信领域.随着研究的深入,其应用已扩展到图像处理[2]、无线传感器网络[3]和地震勘探[4]等领域.
医学 CT图像是 X射线从多个方向对人体检查部位具有一定厚度的层面进行扫描,由探测器接收透过层面的 X线,再经光电和模数变换后输入计算机形成的图像.它是灰度图像,反映了器官和组织对 X线的吸收程度,利于发现体内微观组织的细小病变,已成为医学图像诊断领域中最重要的依据之一.但CT图像在成像和传输过程中,会受到一些外部环境的影响,诸如电子辐射探测接收不佳、散焦模糊、以及图像获取和数字化过程中的干扰等,使得人体组织上的一个点都会映射到 CT图像上的多个点,即 CT图像上的每个点是人体组织的许多点的混合叠加,其对应关系一般称为点扩展函数(point spread function,PSF).换言之,图像在传输过程中,由于受到二维信道的影响,会产生图像模糊问题,使得 CT图像产生退化,影响病变的正常显示及诊断准确率.
恒模盲均衡算法是通信信号处理最常用的算法之一,文献[5]已经对其进行了详细的分析.本文利用图像信号退化过程和码间干扰产生之间的相似性,在文献[6]基础上,通过降维处理将二维信号卷积运算转化为一维信号处理,建立了基于降维医学CT图像恒模代价函数,获得了降维信号的最优估计,再利用升维变换获得图像的估计.该方法避免了图像二维矩阵求逆运算,降低了算法的复杂度,有效消除了点扩展函数的影响,得到了较好的图像恢复效果,实验仿真验证了算法的有效性.
1 数学模型
退化图像ijg是由原始图像ijf通过一个点扩展函数系统ijh,再叠加加性噪声ijn得到的.线性时不变的图像退化模型可表示为
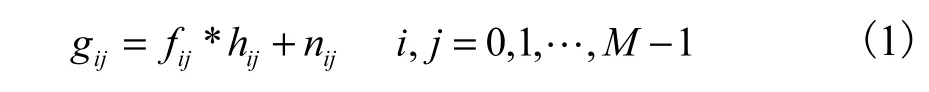
由于计算机中图像的处理都是二维离散的序列,因而为描述方便,图像的退化形式[7]表示为


式中:n为 M2×1的噪声向量;Η为一个分块的M2×M2循环矩阵,每个Hj都是一个M阶矩阵,由周期延拓函数
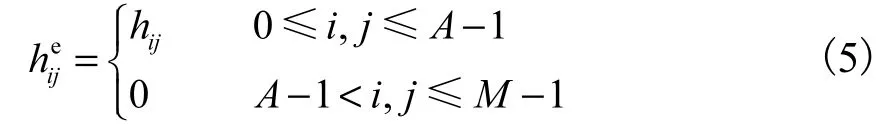
其中,点扩展函数ijh的维数为AA×.
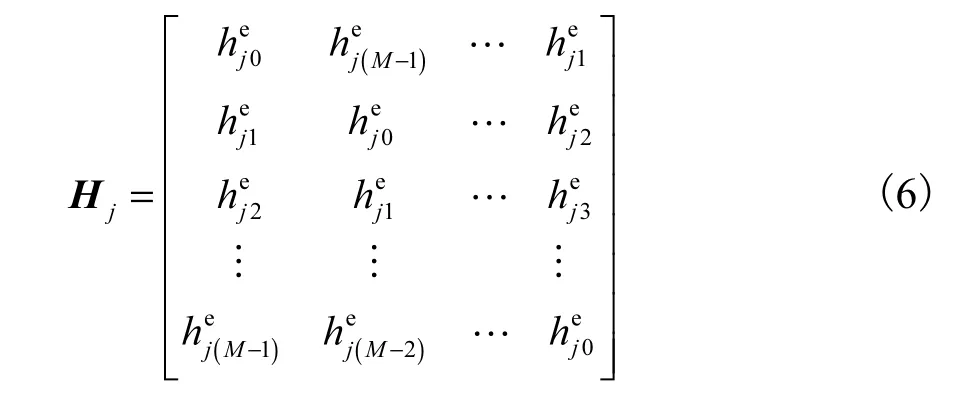
为了利用盲均衡技术实现医学CT图像的恢复,该算法将二维医学 CT图像信号转换为一维信号进行盲均衡,其原理如图1所示.
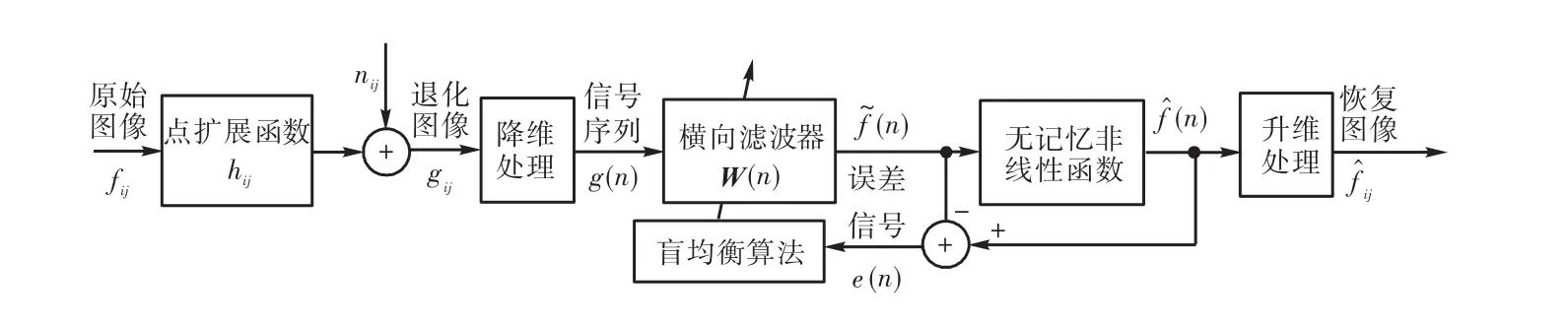
图1 基于降维处理的图像盲均衡算法Fig.1 Diagram of image blind equalization algorithm based on dimension reduction
图1 中,W ( n )是盲均衡器的权值向量;g ( n)为图像降维后的信号序列;e( n)是盲均衡器定义的误差信号为均衡器输出的恢复信号;为估计信号输出;
为原始图像的估计.
为了实现图像降维处理,令

算法中横向滤波器取阶数为L的滤波器,表示为

则有
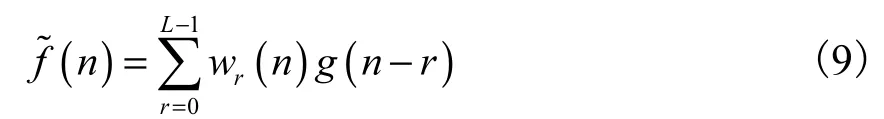
横向滤波器的输入序列矢量 G ( n)为
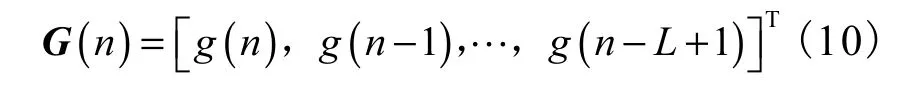

于是,式(9)可写为

为了得到图像的最优估计,获得 W ( n)的最优解,建立关于 W ( n)的代价函数,把 W ( n)的求解转化为一个代价函数的寻优.同时,为了恢复图像,还需要进行相应的升维变换,即

2 恒模代价函数
数字医学CT图像是灰度图像,且具有独立同分布特性[9].图像盲恢复是关于原始图像与点扩展函数的一个不适定性问题[10],Vural等[6]首次利用恒模思想进行图像恢复,提出一种二维图像恒模代价函数.由于本文对图像进行了降维处理,新建立的恒模代价函数为

利用最小均方 (least mean square,LMS) 算法求解代价函数,由于 J ( n)实质上是变量 W ( n)的函数,得到的算法迭代形式为
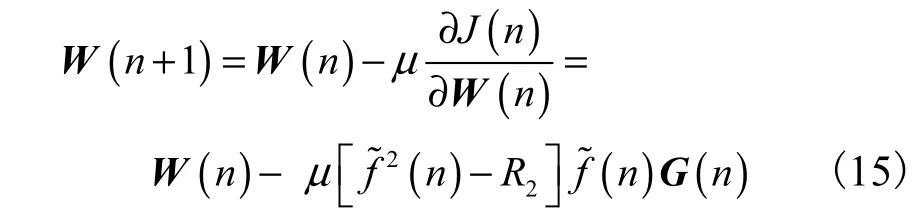
式中μ为步长因子.
为了实现图像的恢复,必须保证式(15)稳态收敛,且具有良好的动态收敛性能.
2.1 稳态收敛性能分析
在恒模盲均衡算法理想收敛情况下,最优权系数应满足的表达式[11]如下.
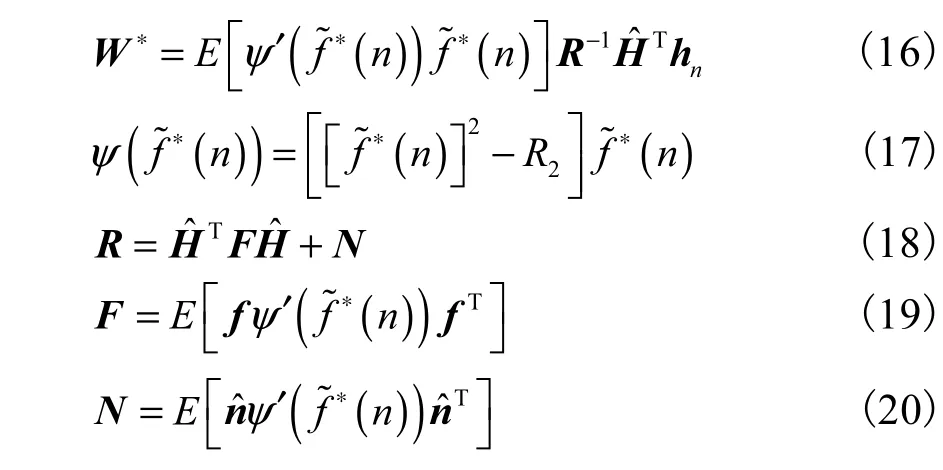

利用Taylor扩展式将
利用 LMS算法对代价函数求解,需求代价函数的梯度,并令其等于0,即
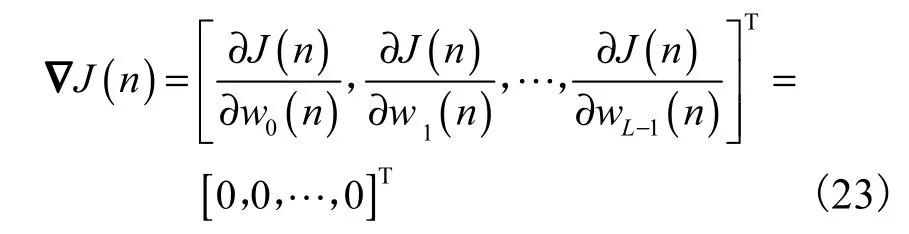
与此同时,代价函数的二阶导数是一个正定的Hessian 矩阵[12],即

由式(25)和Θ的正定性可知,R也是一个正定矩阵,因而R可逆.
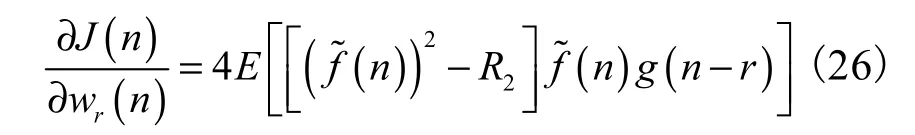
由式(23)和式(26)化简可得


将式(27)和式(28)代入式(22)得所以

将式(11)和(12)代入式(29)得

由于假设图像是独立同分布的[9],因而有
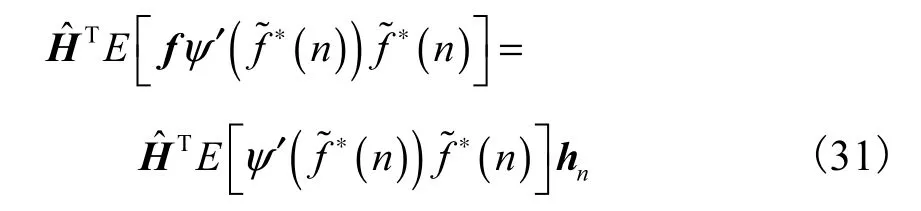
所以将式(31)代入式(30),且当 W ( n) → W*,则可得式(16)的结论.
2.2 动态收敛性能分析
为了讨论算法的动态性能,研究权值 W ( n)逼近最优解 W∗的能力,定义

设λmax是的最大特征根,则权值向量 W ( n )满足

由于图像和噪声互不相干,可知

将式(27)、式(39)和式(40)代入式(41)并取期望得
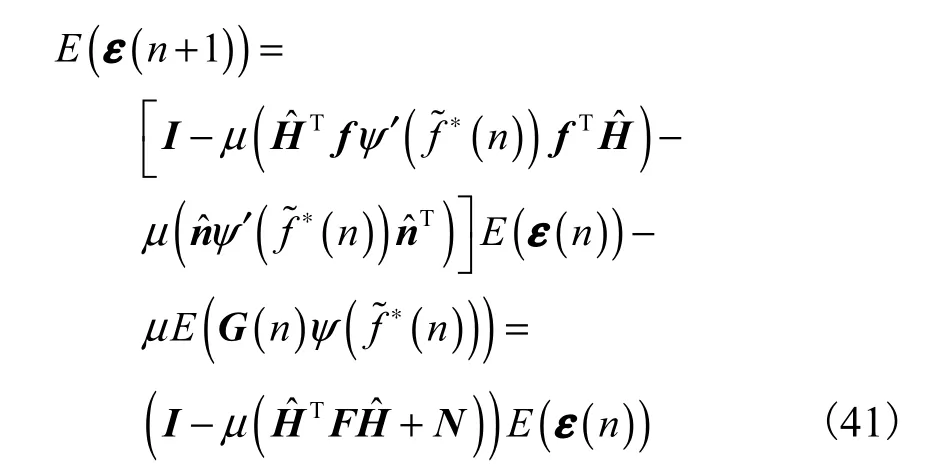
3 实验仿真与分析
1)实验1
实验图像为 256×256个像素的 8,bit,CT图像,如图2(a)所示.CT图像的退化过程是一个近似的高斯过程[13].仿真中,退化函数为一个 20×20的高斯退化模型,其方差20.05 σ = .使用以上PSF模糊后迭加均值为 0、方差为 0.001的高斯白噪声得到退化图像,如图 2(b)所示.横向滤波器的阶数为 11,其初值为有一个位置为 1、其他位置均为 0的单位向量;迭代步长 μ =2× 1 0−8,R= 3 9 320.0.图 2(c)是最大似
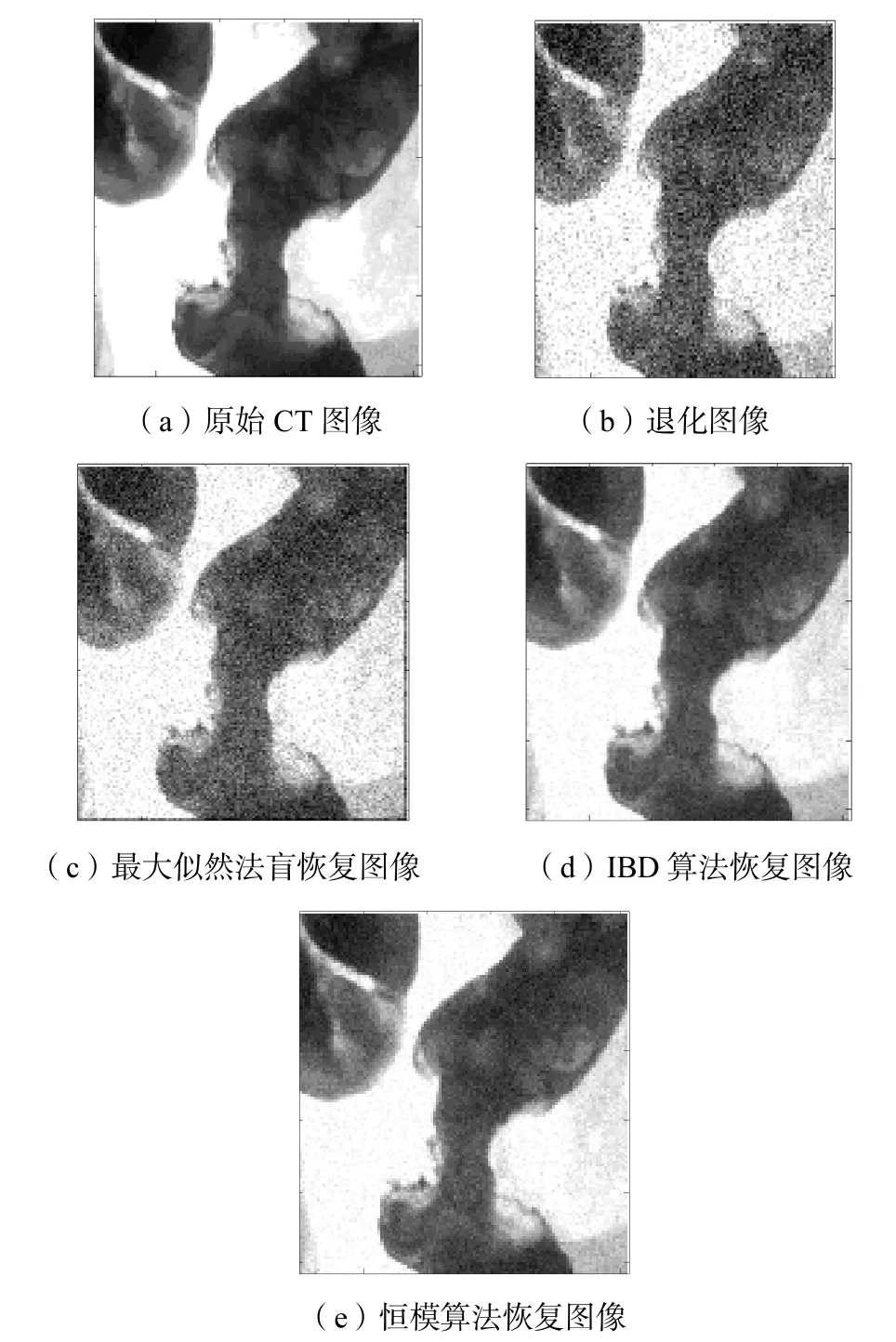
图2 实验1实验数据和结果Fig.2 Experimental data and results of experiment 1
2然法盲恢复图像的恢复效果;迭代盲反卷积(iterative blind deconvolution,IBD)算法的迭代次数为 100,恢复结果如图 2(d)所示,本文提出的恒模算法恢复效果如图2(e)所示.
2)实验2
实验图像是一幅正常额窦 CT图像(矢状位),大小为 256×256个像素,如图 3(a)所示.本例中退化函数取一个 10×10的高斯退化模型,其方差为0.005.使用上述 PSF模糊后迭加均值为 0、方差为0.005的高斯白噪声得到退化图像,如图 3(b)所示.仿真中,横向滤波器的阶数为 21,其初值为[0,… ,0 ,1,0,… 0 ]T;迭代步长 μ =1× 1 0−9,R= 3 9 320.0.
2最大似然法盲恢复图像的恢复效果如图 3(c)所示,IBD 算法的迭代次数为 100,恢复结果如图 3(d)所示,本文提出算法的恢复效果如图3(e)所示.
由图2和图3给出的恢复效果可知,在高信噪比下,本文算法和IBD算法均可获得较好的恢复效果,但信噪比降低时,本文算法的恢复效果要优于 IBD算法.但就运行效率而言,最大似然法和本文算法占有一定的优势,优于IBD算法,本文算法和最大似然法受噪声的影响小,但最大似然法的恢复效果依赖于估计模型的精度和模型的阶数,模型阶数低时效果欠佳,模型阶数较高时影响运算速度.
为了定量检测图像恢复的效果,本文采用峰值信噪比(peak signal to noise ratio,PSNR)作为评价图像恢复的指标,其定义[14]为
峰值信噪比表征了均衡图像对于目标的逼近程度,峰值信噪比越高,表明恢复效果越好,越接近原始图像.各种算法的性能比较如表1所示.
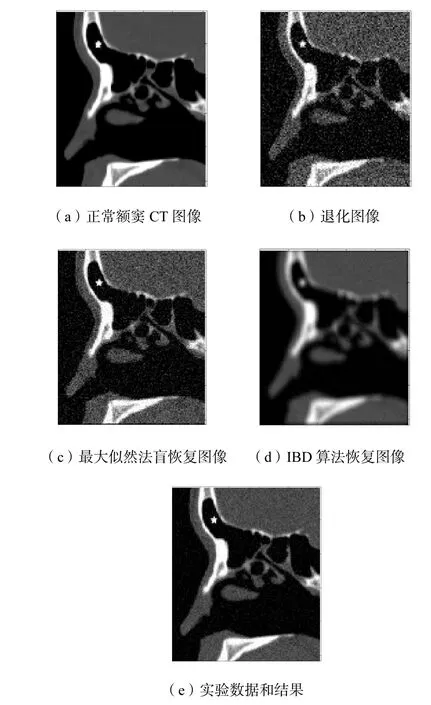
图3 实验2的实验数据和结果Fig.3 Experimental data and results of experiment 2
实验结果表明,IBD算法由于需要对图像和点扩展函数进行交替迭代,影响了算法的运算效率,恢复效果还具有一定优势,但对噪声的鲁棒性差.最大似然法为了提高恢复效果需增大模型阶数,同时也增加了运算量.本文提出的基于降维处理的恒模算法避免了算法的交替迭代,减少了运算量,加快了算法收敛,改善了恢复效果,且具有较好的鲁棒性.

表1 各种算法性能比较Tab.1 Performance comparison of algorithms
4 结 语
本文提出的恒模 CT图像盲均衡算法通过信号的变换将二维图像转换为一维信号处理,避免了图像矩阵的求逆运算,降低了算法的复杂度.本文重点分析了算法的稳态收敛性能,表明建立的代价函数理论上能收敛到维纳解,讨论了算法的动态收敛能力,即在步长满足要求的前提下,能够保证算法的动态收敛.理论分析为算法的进一步应用研究提供了理论依据.最后,通过计算机仿真验证了算法的有效性.
[1] Sato Y. A method of self-recovering equalization for multiple amplitude modulation schemes[J]. IEEE Trans on Communication,1975,23(6):679-682.
[2] Giannakis G B,Heath Jr R W. Blind identification of multichannel FIR blurs and perfect image restoration[J].IEEE Trans on Image Processing,2000,9(11):1877-1896.
[3] Giannakis G B,Heath Jr R W. Blind channel estimation and equalization in wireless sensor networks based on correlations among sensors[J]. IEEE Trans on Signal Processing,2005,53(4):1511-1519.
[4] Bruneau M,Reinhorn A M,Constantinou M C,et al.The university at buffalo(UB)node of the NEES network:A versatile high performance testing facility towards real-time dynamic hybrid testing[C]// 12th European Conference on Earthquake Engineering. London,UK,2002:1-8.
[5] LeBlanc J,Fijalkow I,Johnson C. CMA fractionally spaced equalizers:Stationary points and stability under IID and temporally correlated sources[J]. International Journal of Adaptive Control and Signal Processing,1998,32(12):135-155.
[6] Vural C,Sethares W A. Blind image deconvolution via
dispersion minimization[J]. Digital Signal Processing,2006,16(2):137-148.
[7] 黄 飞,金伟其,曹峰梅,等. 相向运动条件下图像的辐射状退化及其复原研究[J]. 电子学报,2005,33(9):1710-1713.Huang Fei,Jin Weiqi,Cao Fengmei,et al. Simulation and restoration study on radiant degradation image under lengthwise relative motion[J]. Acta Electronica Sinica,2005,33(9):1710-1713(in Chinese).
[8] 江玲玲,冯象初,殷海青. 基于 Besov空间的图像盲复原算法[J]. 数据采集与处理,2008,23(6):678-682.Jiang Lingling,Feng Xiangchu,Yin Haiqing. Blind image restoration algorithm based on Besov spaces[J].Journal of Data Acquisition & Processing,2008,23(6):678-682(in Chinese).
[9] Samarasinghe P D,Kennedy R A. Minimum kurtosis CMA deconvolution for blind image restoration[C] //4th International Conference on Information and Automation for Sustainability. Colombo,Srilanka,2008:271-276.
[10] Chan T,Wong C. Convergence of the alternating minimization algorithm for blind deconvolution [J].Elsevier,Linear and Its Application,2000,316(3):259-285.
[11] Li Ye,Liu K J Ray. Static and dynamic convergence behavior of adaptive blind equalizers[J]. IEEE Trans on Signal Processing,1996,44(11):2736-2745.
[12] Mizutani Eiji,Dreyfus S E. Second-order stagewise backpropagation for Hessian-matrix analyses and investigation of negative curvature[J]. Neural Networks,2008,21(2/3):193-203.
[13] Jiang Ming,Wang Ge,Skinner M W,et al. Blind deblurring of spiral CT images[J]. IEEE Trans on Medical Imaging,2003,22(7):837-845.
[14] Li Dalong,Simske S. Atmospheric turbulence degradedimage restoration by kurtosis minimization[J]. IEEE Geoscience and Remote Sensing Letters,2009,6(2):244-247.
