切削条件对超精密切削过程影响的数值模拟

景秀并，林 滨，张大卫

(天津大学先进陶瓷与加工技术教育部重点实验室，天津 300072)

超精密加工过程涉及到弹性力学、塑性力学、断裂力学以及热力学和摩擦学等[1]．加工表面质量受到刀具形状、切削深度和切削速度等因素的影响．超精密切削过程机理的研究分为理论分析和试验验证[2]．通过试验可以获得切削力的大小、切削温度的分布和已加工表面完整性等．从 20世纪 70年代有限元方法开始应用于研究切削过程以来，国际上对金属切削工艺的有限元模拟逐步深入．澳大利亚悉尼大学和美国Auburn大学对有限元分析正交切削工艺中的切屑分离准则做了深入的研究[3-4]；Woona等[5]利用有限元研究了超精密切削过程中刀尖半径对切削力和切屑形成的影响；Anurag等[6]利用内部状态变量塑性模型，研究了材料测试模式对难加工材料的影响．我国清华大学和哈工大亦开展了这方面的研究工作[7-8]．通过有限元方法分析切削过程能够获得加工表面位移变化曲线，有利于研究切削过程的机理．

切削加工过程有限元模拟涉及有限元方程的选择、切屑分离标准的确定、刀屑表面接触问题的处理、动态自适应网格技术、适用于大型计算的并行机与网络计算技术等．精密切削过程切削条件对已加工表面完整性有着很大的影响．本文采用 Lagrange有限元方程、修正的JC本构关系和Cockroft-Latham切削断裂标准，建立了精密切削的三维有限元模型．采用此模型研究探讨了刀具几何特性、切削速度、切削用量等因素对加工表面质量的影响．

1 有限元模型的建立

1.1 三维切削有限元模拟的模型

有限元模型的建立就是将被研究对象的几何外形、材料特性和研究对象内部以及与周围环境之间的相互作用有机结合的过程．为了便于建立精密切削三维有限元分析模型，假设切削过程具备如下的条件：①正交切削，在切削过程形成连续的切屑，无积屑瘤存在；②工件材料为各向同性的连续固体介质，工件材料发生变形符合Von Mises应力屈服准则；③在切削过程中，假设切削温度不足以导致工件材料发生化学变化．有限元模型如图1所示．刀具垂直方向运动受限制，以一定的切削速度沿 y向运动，工件右边单元水平方向固定，底部单元完全固定．切屑和工件摩擦对切削过程有显著的影响，但是对于介观切削由于试验和测试条件的限制，微摩擦相关的研究还不成熟，在模型中，刀具和切屑的摩擦采用库伦摩擦，摩擦系数为0.3[9]．

图1 有限元模型和边界条件Fig.1 Finite element model and boundary condition

1.2 修正工件材料的本构关系

超精密切削中，切屑、剪切面处有着较大塑性应变和极高的应变率，在材料发生塑性变形中，材料的流动应力受到温度、等效应变速率和等效应变等的影响，因此在三维仿真中，综合考虑这些因素，将工件的流动应力看作应变、应变率和温度的函数[10]，其JC式唯象本构方程可表示为

式中：σ为工件材料的流动应力；ε为工件材料的塑性应变；ε˙为工件材料的应变率；m、n分别为材料指数和应变率指数；tmelt和 troom分别为工件的融化温度和环境温度；A、B和C分别为应力常数、应变硬化系数和应变系数．由于金属材料在超精密切削过程中具有强烈的尺度效应，采用应变梯度(strain gradient，SG)理论可以预测出尺度效应，基于 SG理论对 JC模型进行修正，建立能够描述超精密加工的材料本构关系[11]为

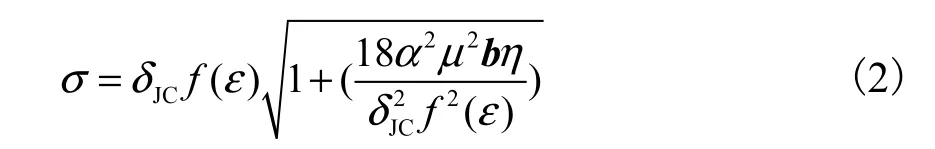
式中：α为 Taylor系数，其值约为 0.3；μ为剪切模量；b为Burgers矢量；η为应变梯度；ε为应变．

1.3 有限元算法的选择

从数值模拟的角度来看，适用于有限元模拟的算法有 Lagrange方法、Euler方法和 ALE[12]方法． Lagrange方法适用于固体分析，有限元网络由材料单元组成，所有的网络准确地描述了所分析物体的几何形状，这些网格随着工件的变形而变化，这种方法在模拟材料的无约束流动时很方便．Euler方法更适合在一个可以控制的体积内描述流体的变形．由于切削加工中切屑的形状是不固定的，因此 Euler方法不适合模拟切削过程．ALE方法兼备 Lagrange方法和Euler方法两者特长．目前在切削加工有限元模拟中大部分采用 Lagrange方法，在本文的有限元模拟中也采用了塑性大变形 Lagrange[13]方法，导出热弹塑性大变形耦合方程为

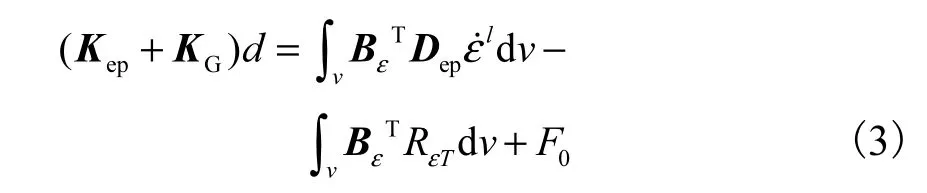
式中：d为节点速度；TRε为分项应变率；epK 为弹塑性刚度矩阵为几何刚度矩阵，为预应力矩阵；为接触面上合力的变化率，N为单位形状矩阵．

1.4 仿真采用的分离准则

切削加工是被加工材料不断产生分离的过程，合理的分离准则只有真实地反映切削加工材料的力学和物理性质，才能得到合理的结果．目前人们在有限元模拟中提出了许多模拟准则，这些准则可以分为 2种类型：几何准则和物理准则．几何准则主要通过变形体的几个尺寸的变化来判断分离与否；物理准则主要是基于制定的一些物理量的值是否达到了临界点为工件节点力的变化率而建立的．本文应用 Cockroft-Latham切削断裂标准，通过高温拉伸试验计算出断裂塑性性能，并同金属材料变形断裂所需的能量建立映射关系，将其作为判断金属材料延伸断裂的临界能量值，即

式中：εf为高温拉伸断裂时的总应变；σ为等效应力；ε为等效应变；σ∗为最大拉伸应力；Cr为临界断裂值．当节点经历的拉伸应力超过压缩应力的 10%时，该节点处产生分离．

2 结果和讨论

以所建立的考虑尺度效应的本构关系为基础，应用 Fortran语言，在对有限元软件本构关系进行二次开发，对不同切削条件进行仿真，工件材料选用 AL-1100，刀具设定为刚体，工件材料力学性能参数见表 1．

表1 材料力学性能参数Tab.1 Performance parameters of mechanical properties

超精密加工中影响加工精度和加工效率的主要是刀具几何特性(前角 γ0、后角 α0和刀尖半径 ρ)、切削深度(ap)和切削速度．有限元模拟仿真切削参数见表2，工件材料物理特性见表3．

表2 仿真切削参数Tab.2 Parameters of cutting simulation

表3 工件材料物理特性Tab.3 Physical characteristics of workpiece

2.1 刀具后角对切削的影响

刀具后角对加工表面质量有很大的影响，分别选取不同后角进行计算，结果如图2所示．从图2可以看出，随着刀具后角的增加，工件表面的最大位移变化量随着后角的增大而降低(从 0°时 0.629,μm 减少到 10°时 0.067,μm)．这是因为增加刀具后角，可减少刀具后面和加工表面的摩擦，降低工件加工表面的残余应力和表面粗糙度，提高加工质量．但是为了保证刀具强度，后角一般取6°左右．

2.2 刀尖半径对切削的影响

刀具刀尖半径现象是超精密加工区别于传统切削的一个显著特性，对不同刀具刀尖半径时超精密切削过程进行计算，结果如图 3所示．由图 3可以看出，刀尖半径对表面质量影响很大，工件表面最大位移变化量随着刀具刀尖半径的减小而减小，这是因为刀尖半径对加工表面挤压和摩擦的程度与切削刃的锋利度有关，切削刃越钝，加工表面的变形越大，加工表面质量越差．

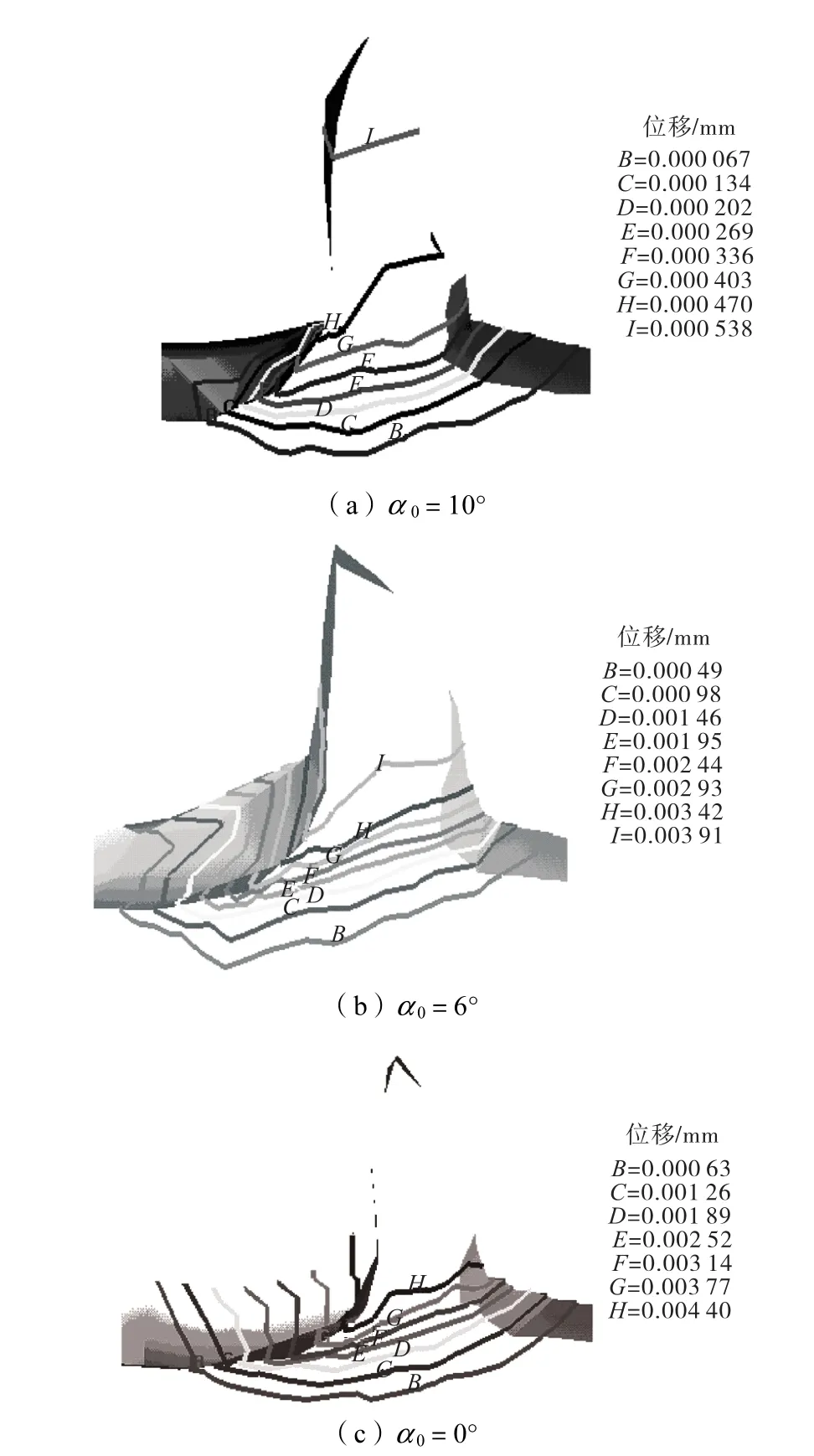
图2 不同后角时的模拟结果 (γ0＝5°、ρ＝4 μm、ap＝2 μm)Fig.2 Simulation results at various clearance angles(γ 0＝5°，ρ＝4 μm，ap＝2 μm)

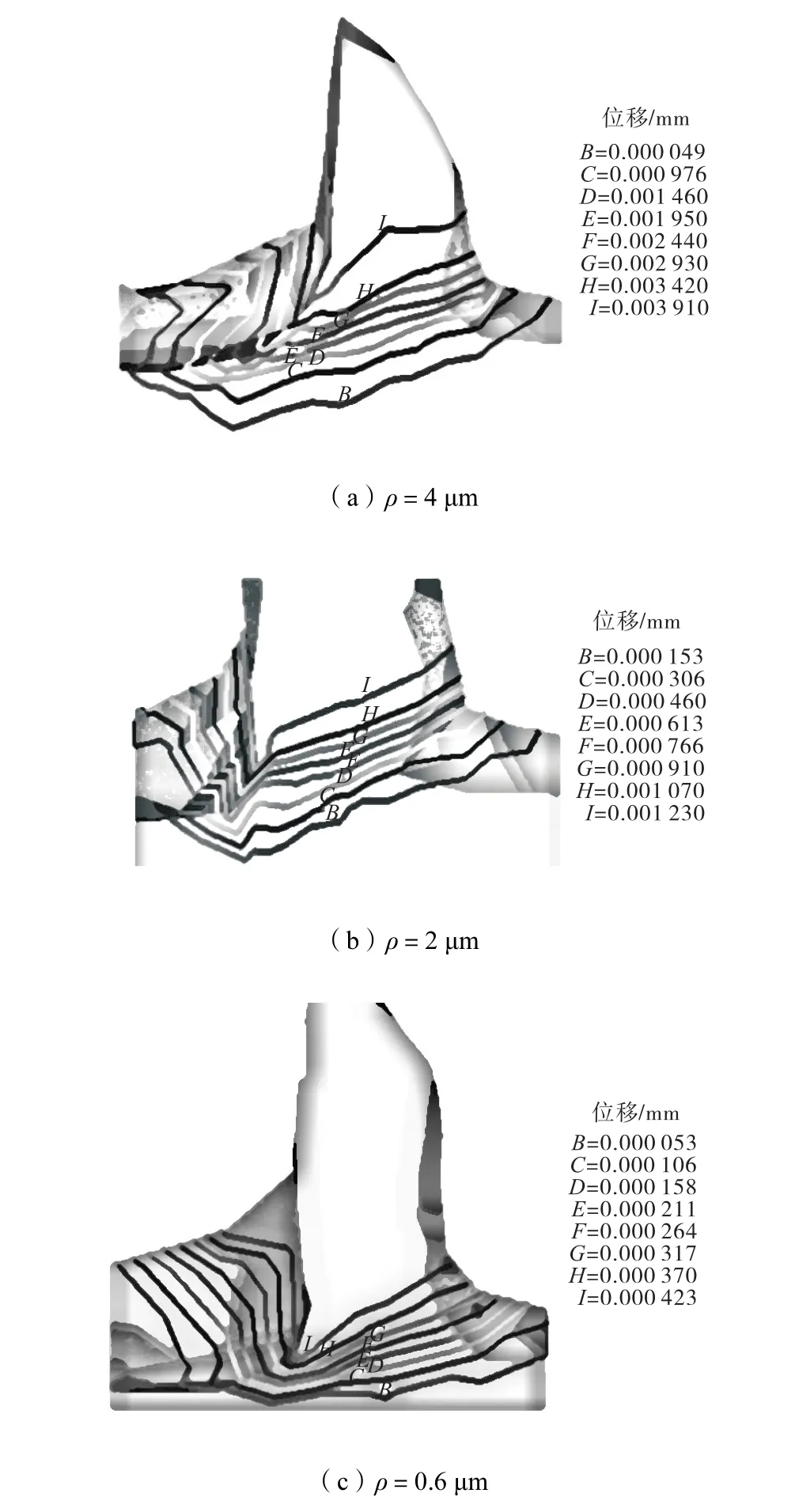
图3 不同刀尖半径时的模拟结果(γ0＝5°、α＝6°、ap＝2 µm)Fig.3 Simulation results at various tool edge radiuses(γ0＝5°，α＝6°，ap＝2 µm)

2.3 切削深度对切削的影响

切削深度主要影响加工效率，对加工表面质量的影响不明显．但当切削深度非常小时正常切削不能进行．图4为不同切削深度时的模拟结果．由图4可以看出，当切削深度为0.3ρ时并不产生切屑，该结果与 Kim等[14]研究相近，即最小切削厚度约为切削刃半径的30%．工件表面节点位移随着切削深度的增大略有增大，当 ap＝0.3ρ时由于常挤压滑过加工表面而在加工表面上引起附加的塑性变形，从而使表面节点位移增大．所以超精密加工不能选用过小的切削深度．增大切削深度可以提高切削效率，但过大的切削深度也会因切削力、切削热剧增而影响加工精度和表面质量，一般情况切削深度和刀尖半径相当．

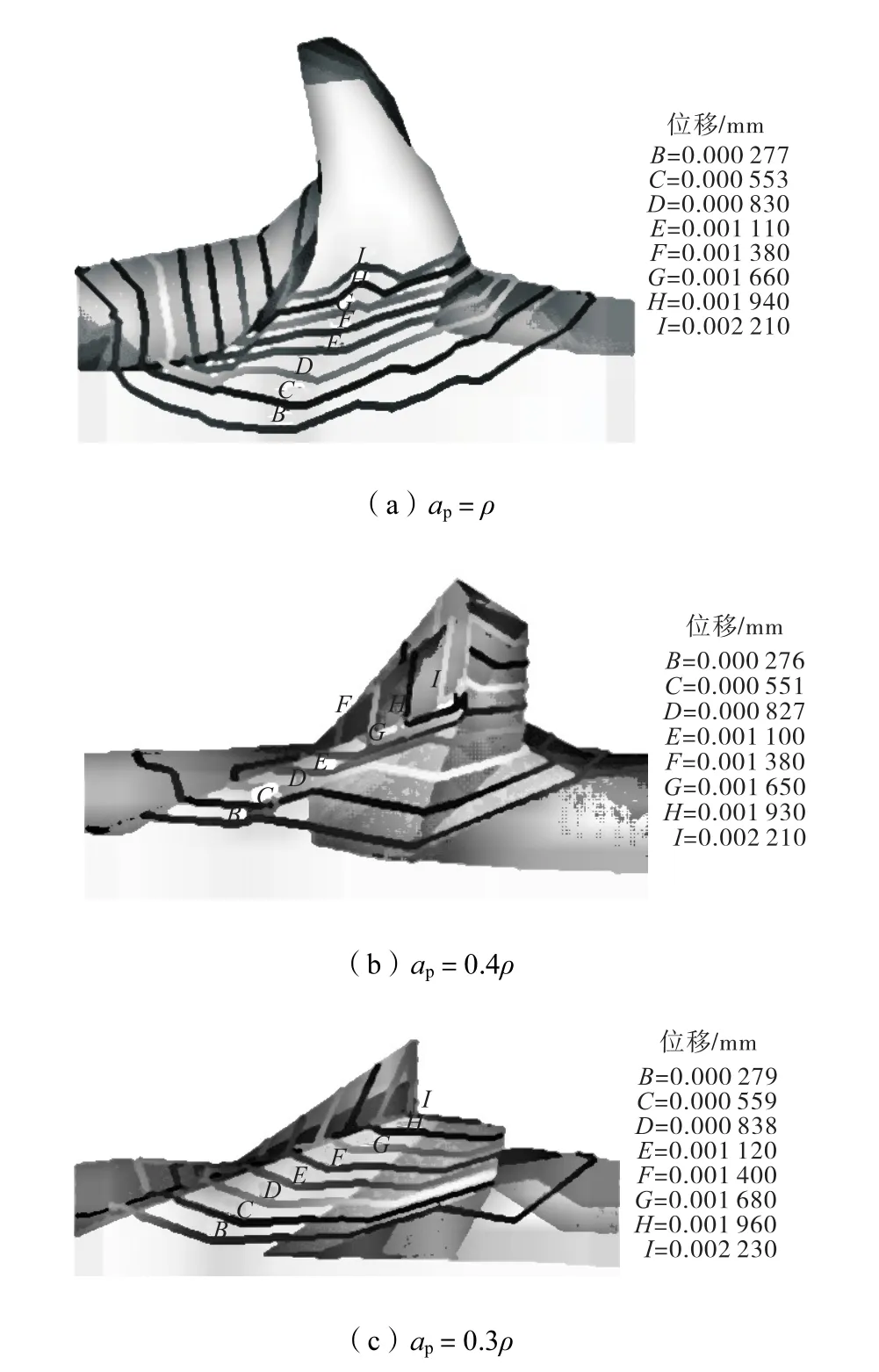
图4 不同切削深度时的模拟结果(α0＝5°、γ0＝6°、ρ＝2 µm)Fig.4 Simulation results at various cutting depths(α0＝5°，γ0＝6°，ρ＝2 µm)

2.4 切削速度对切削的影响

加工塑性材料时，切削速度对表面质量和加工效率的影响非常显著．图 5为不同切削速度的模拟结果．由图 5可以看出，表面节点位移随着切削速度的增大而降低，但是如果切削速度太大，节点位移反而增大．这时因为切削速度较低易产生鳞刺，表面质量会降低，但是切削速度太大时切削温度随之升高，表面质量也会降低．因此用较高的切削速度，既可提高生产率，又可提高加工表面质量．加工铝合金时切削速度一般为150,m/min左右．

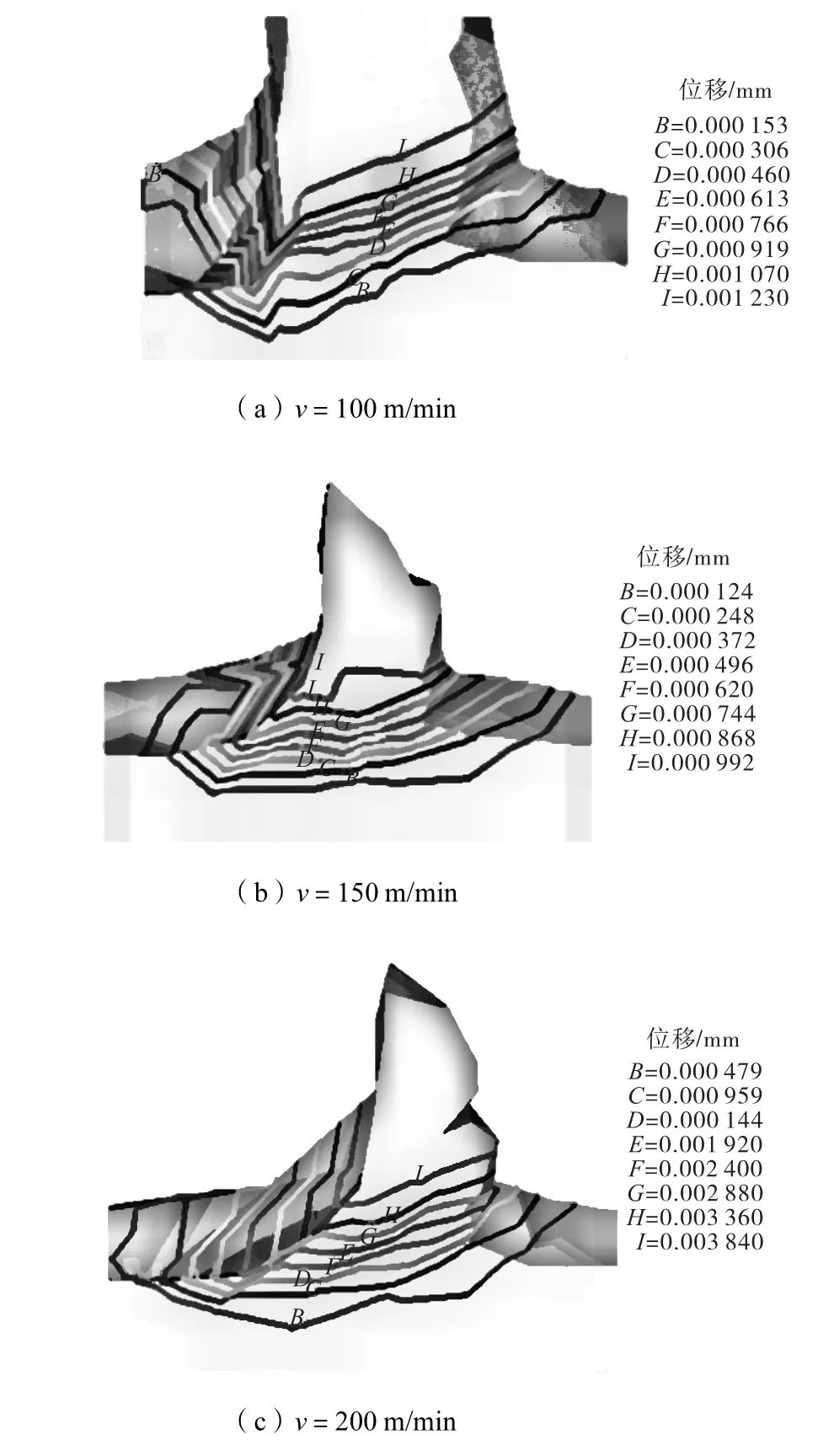
图5 不同切削速度时的模拟结果(γ0＝6°、ρ＝4 µm、ap＝2 µm)Fig.5 Simulation results at various cutting velocities(γ0＝6°，ρ＝4 µm，ap＝2 µm)

3 切削试验与仿真结果比较

为了对仿真结果进行验证，在 MOORE 250UPL单点金刚石车床上进行了切削试验，并对加工后的表面质量采用 Veeko 白光干涉仪进行检测．需要说明的是考虑到超精密金刚石切削工况，仿真试验中从工件表面变形状态入手分析加工表面粗糙度．试验中，试件材料为铝合金，刀具材料为单点金刚石，刀具前角为 5°，刀具后角为 6°，刀尖半径为 0.6,µm，切深为2,µm，切削速度为 150,m/min．加工表面测试与仿真结果如图 6所示．超精密切削试验获得的表面粗糙度测试结果Ry的值和仿真表面吻合很好．

图6 试验结果和模拟结果比较Fig.6 Comparison between experimental and simulation results

4 结 论

(1) 针对超精密加工过程中的尺寸效应，基于应变梯度理论对 JC模型进行了修正，建立了能够描述超精密加工的材料本构关系模型．

(2) 运用所建立的模型，对不同切削条件进行了仿真，结果表明：增加刀具后角和减小刀尖半径，加工表面的最大位移有所下降；切削深度对加工表面质量的影响不明显，为了保证加工效率，切削深度一般和刀具刀尖半径相当；切削速度影响表面质量和切削效率，速度太大或太小都会影响加工表面质量，加工铝合金时切削速度为150,m/min左右．

(3) 超精密切削试验获得的表面粗糙度测试结果Ry和仿真表面粗糙度吻合很好．

［1］ 吴玉华. 金属切削加工技术[M]. 北京：机械工业出版社，1998.Wu Yuhua. Metal Cutting Technology[M]. Beijing：China Machine Press，1998(in Chinese).

［2］ 翟元盛，梁迎春，王洪祥. 精密切削过程三维有限元分析[J]. 工具技术，2007，41(6)：55-57.Zhai Yuansheng，Liang Yingchun，Wang Hongxiang.Finite element analysis of three-dimensional precision cutting[J]. Tool Engineering，2007，41(6)：55-57(in Chinese).

［3］ Zhang Liargchi C. On the separation criteria in the simulation of orthogonal metal cutting using the finite element method[J]. Journal of Materials Processing Technology，1999，88/89：273-278.

［4］ Huang J M，Blank J T. An evaluation of chip separation criteria for the FEM simulation of machining[J]. ASME Journal of Manufacturing Science and Engineering，1996，118(4)：545-554.

［5］ Woona K S，Rahmana M，Fang F Z，et al. Investigations of tool edge radius effect in micromachining：A FEM simulation approach[J]. Journal of Materials Processing Technology，2008，195(1/2/3)：204-211.

［6］ Anurag S，Guo Y B，Horstemeyer M F. The effect of materials testing modes on finite element simulation of hard machining via the use of internal state variable plasticity model coupled with experimental study[J]. Computers and Structures，2009，87(5/6)：303-317.

［7］ 王洪祥，汤敬计，廖世宾，等，超精密切削切屑形成过程的三维有限元仿真[J].哈尔滨工业大学学报，2005，37(3)：293-295.Wang Hongxiang，Tang Jingji，Liao Shibin，et al. 3-D finite element simulation of chip formation in ultraprecision cutting process[J]. Journal of Harbin Institute of Technology，2005，37(3)：293-295(in Chinese).

［8］ 方 刚，曾 攀. 金属正交切削工艺的有限元模拟[J]. 机械科学与技术，2003，22(4)：641-645.Fang Gang，Zeng Pan，FEM simulation of orthogonal metal cutting process[J]. Mechanical Science and Technology，2003，22(4)：641-645(in Chinese).

［9］ Kim K W，Lee W Y，Sin H C. A finite element anaysis for the characteristics of temperature and stress in micromachining considering the size effect[J]. International Journal of Machine Tool & Manufacture，1999，39(9)：1507-1524.

［10］ Yang Q，Mota A，Ortiz M. A class of variational strain localization finite elements[J]. International Journal for Numerical Methods in Engineering，2005，62(8)：1013-1037.

［11］ 景秀并，张大卫，林 滨. 介观尺度切削过程的材料本构关系分析[J]. 兵工学报，2010，31(5)：620-623.Jing Xiubing，Zhang Dawei，Lin Bin. Analysis on constitutive relation in meso-scale cutting process[J]. Acta Armamentarii，2010，31(5)：620-623(in Chinese).

［12］ Movahhedy M，Gadala M S，Altintas Y. Simulation of the orthogonal metal cutting process using an arbitrary Lagrangian-Eulerian finite-element method[J]. Journal of Materials Processing Technology，2000，103(2)：267-275．

［13］ Lin Zone-Ching，Lai Wun-Ling，Lin H Y，et al. The study of ultraprecision machining and residual stress for NiP alloy with different cutting speeds and depth of cut[J]. Journal of Materials Processing Techonogy，2000，97(1/2/3)：200-210.

［14］ Kim C J，Mayor J R，Ni J. A static model of chip formation in microscale milling[J]. ASME Journal of Manufacturing Science and Engineering，2004，126(4)：710-718.